Table 6.3, calculation on page 91 and 92 and Table 6.4. For the matrix calculation, we used proc iml. Proc iml is an interactive matrix language.
data table6_3; input carbohydrate age weight protein; cards; 33 33 100 14 40 47 92 15 37 49 135 18 27 35 144 12 30 46 140 15 43 52 101 15 34 62 95 14 48 23 101 17 30 32 98 15 38 42 105 14 50 31 108 17 51 61 85 19 30 63 130 19 36 40 127 20 41 50 109 15 42 64 107 16 46 56 117 18 24 61 100 13 35 48 118 18 37 28 102 14 ; run; proc iml; use table6_3; read all; y = carbohydrate; n = nrow(y); one = j(n, 1, 1); x = one || age || weight || protein; y = carbohydrate; xy = t(x)*y; print xy[label="X'Y"];
X'Y
752
34596
82270
12105
xx = t(x)*x;
print xx[label="X'X"];
X'X
20 923 2214 318
923 45697 102003 14780
2214 102003 250346 35306
318 14780 35306 5150
b = inv(xx)*xy;
xinv = inv(xx);
print b ;
print xinv[label="(X'X)^(-1)" format=6.4];
B
36.960056
-0.113676
-0.228017
1.9577126
(X'X)^(-1)
4.8158 -.0113 -.0188 -.1362
-.0113 0.0003 0.0000 -.0004
-.0188 0.0000 0.0002 -.0002
-.1362 -.0004 -.0002 0.0114
bxy = t(b)*xy;
sigma2 = 1/(n-4)*t(y-x*b)*(y-x*b);
V = sigma2*xinv;
std = sqrt(vecdiag(V));
final = b || std;
alab = {'constant', 'age', 'weight', 'protein'};
blab = {'Estimate b_j', 'Standard error'};
print 'Estimates for model (6.6)';
print final[rowname=alab colname=blab label='' format=15.3];
Estimates for model (6.6)
Estimate b_j Standard error
constant 36.960 13.071
age -0.114 0.109
weight -0.228 0.083
protein 1.958 0.635
x1 = one || weight || protein;
x1y = t(x1)*y;
print x1y[label="X'Y"];
X'Y
752
82270
12105
x1x1 = t(x1)*x1;
print x1x1[label="X'X"];
X'X
20 2214 318
2214 250346 35306
318 35306 5150
b1 = inv(x1x1)*x1y;
print b1;
B1
33.13032
-0.221649
1.8242912
b1x1y = t(b1)*x1y;
imprv = bxy - b1x1y;
resid = t(y-x*b)*(y-x*b);
mse = resid/16;
print resid mse;
quit;
RESID MSE
567.66286 35.478929
Table 6.5 on page 93.
proc reg data = table6_3 ;
model carbohydrate = age weight protein ;
test_on_age: test age;
run;
quit;
Test test_on_age Results for Dependent
Variable carbohydrate
Mean
Source DF Square F Value Pr > F
Numerator 1 38.35907 1.08 0.3139
Denominator 16 35.47893
Table 6.6 on page 96.
data table6_6;
input control treatmentA treatmentB;
datalines;
4.17 4.81 6.31
5.58 4.17 5.12
5.18 4.41 5.54
6.11 3.59 5.5
4.5 5.87 5.37
4.61 3.83 5.29
5.17 6.03 4.92
4.53 4.89 6.15
5.33 4.32 5.8
5.14 4.69 5.26
;
run;
data table6_6a;
set table6_6;
control2 = control*control;
treatmenta2 = treatmenta*treatmenta;
treatmentb2 = treatmentb*treatmentb;
run;
proc means data = table6_6a sum;
var control control2
treatmenta treatmenta2
treatmentb treatmentb2;
run;
Variable Sum --------------------------- control 50.3200000 control2 256.2702000 treatmentA 46.6100000 treatmenta2 222.9185000 treatmentB 55.2600000 treatmentb2 307.1296000 ---------------------------
Table 6.8 on page 100.
data table6_8; length group $12; input group weight; datalines; Control 4.17 Control 5.58 Control 5.18 Control 6.11 Control 4.5 Control 4.61 Control 5.17 Control 4.53 Control 5.33 Control 5.14 TreatmentA 4.81 TreatmentA 4.17 TreatmentA 4.41 TreatmentA 3.59 TreatmentA 5.87 TreatmentA 3.83 TreatmentA 6.03 TreatmentA 4.89 TreatmentA 4.32 TreatmentA 4.69 TreatmentB 6.31 TreatmentB 5.12 TreatmentB 5.54 TreatmentB 5.5 TreatmentB 5.37 TreatmentB 5.29 TreatmentB 4.92 TreatmentB 6.15 TreatmentB 5.8 TreatmentB 5.26 ; run; proc glm data = table6_8; class group; model weight = group /intercept ss3; lsmeans group /stderr ; run; quit;
Dependent Variable: weight
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 3 775.8262100 258.6087367 665.50 <.0001
Error 27 10.4920900 0.3885959
Uncorrected Total 30 786.3183000
Source DF Type III SS Mean Square F Value Pr > F
Intercept 1 772.0598700 772.0598700 1986.79 <.0001
group 2 3.7663400 1.8831700 4.85 0.0159
Least Squares Means
weight Standard
group LSMEAN Error Pr > |t|
Control 5.03200000 0.19712837 <.0001
TreatmentA 4.66100000 0.19712837 <.0001
TreatmentB 5.52600000 0.19712837 <.0001
Table 6.9 on page 101, calculation on page 102 to 104 and table 6.10 on page 104. As before, we used proc iml to perform all the intermediate matrix calculations.
data table6_9; input factorA $ factorB $ data; datalines; A1 B1 6.8 A1 B1 6.6 A1 B2 5.3 A1 B2 6.1 A2 B1 7.5 A2 B1 7.4 A2 B2 7.2 A2 B2 6.5 A3 B1 7.8 A3 B1 9.1 A3 B2 8.8 A3 B2 9.1 ; run; proc sql; select *, sum(data) as total from (select *, sum(data) as total from table6_9 group by factorb) group by factora; quit;
factorA factorB data total total ------------------------------------------------ A1 B1 6.6 45.2 24.8 A1 B1 6.8 45.2 24.8 A1 B2 6.1 43 24.8 A1 B2 5.3 43 24.8 A2 B2 7.2 43 28.6 A2 B1 7.5 45.2 28.6 A2 B2 6.5 43 28.6 A2 B1 7.4 45.2 28.6 A3 B2 8.8 43 34.8 A3 B1 9.1 45.2 34.8 A3 B1 7.8 45.2 34.8 A3 B2 9.1 43 34.8
Before using proc iml, we first used proc glmmod to generate all the dummy variables for the design matrix.
proc glmmod data = table6_9 outdesign=Design; class factora factorb; model data = factora|factorb ; run;
Parameter Definitions
Name of CLASS Variable Values
Column Associated factor factor
Number Effect A B
1 Intercept
2 factorA A1
3 factorA A2
4 factorA A3
5 factorB B1
6 factorB B2
7 factorA*factorB A1 B1
8 factorA*factorB A1 B2
9 factorA*factorB A2 B1
10 factorA*factorB A2 B2
11 factorA*factorB A3 B1
12 factorA*factorB A3 B2
Design Points
Observation Column Number
Number data 1 2 3 4 5 6 7 8 9 10 11 12
1 6.8 1 1 0 0 1 0 1 0 0 0 0 0
2 6.6 1 1 0 0 1 0 1 0 0 0 0 0
3 5.3 1 1 0 0 0 1 0 1 0 0 0 0
4 6.1 1 1 0 0 0 1 0 1 0 0 0 0
5 7.5 1 0 1 0 1 0 0 0 1 0 0 0
6 7.4 1 0 1 0 1 0 0 0 1 0 0 0
7 7.2 1 0 1 0 0 1 0 0 0 1 0 0
8 6.5 1 0 1 0 0 1 0 0 0 1 0 0
9 7.8 1 0 0 1 1 0 0 0 0 0 1 0
10 9.1 1 0 0 1 1 0 0 0 0 0 1 0
11 8.8 1 0 0 1 0 1 0 0 0 0 0 1
12 9.1 1 0 0 1 0 1 0 0 0 0 0 1
Now using the data set that was created by proc glmmod, we can perform the matrix calculations using proc iml.
proc iml; use design; read all; n = nrow(data); x = col1 || col3 || col4 || col6 || col10 || col12; print 'model (6.9)'; print x;
model (6.9)
X
1 0 0 0 0 0
1 0 0 0 0 0
1 0 0 1 0 0
1 0 0 1 0 0
1 1 0 0 0 0
1 1 0 0 0 0
1 1 0 1 1 0
1 1 0 1 1 0
1 0 1 0 0 0
1 0 1 0 0 0
1 0 1 1 0 1
1 0 1 1 0 1
y = data; xty = t(x)*y; xtx = t(x)*x; b = inv(xtx)*xty; print xty[label="X'Y"] xtx[label="X'X"] b;
X'Y X'X B
88.2 12 4 4 6 2 2 6.7
28.6 4 4 0 2 2 0 0.75
34.8 4 0 4 2 0 2 1.75
43 6 2 2 6 2 2 -1
13.7 2 2 0 2 2 0 0.4
17.9 2 0 2 2 0 2 1.5
bxy = t(b)*xty;
print bxy[label="b'X'y"];
b'X'y
662.62
print 'model (6.10)';
x10 = col1 || col3 || col4 || col6;
y = data;
xtx10 = t(x10)*x10;
xty10 = t(x10)*y;
b10 = inv(xtx10)*xty10;
print xtx10 xty10 b10[format=6.3];
XTX10 XTY10 B10
12 4 4 6 88.2 6.383
4 4 0 2 28.6 0.950
4 0 4 2 34.8 2.500
6 2 2 6 43 -0.367
bxy10 = t(b10)*xty10;
print bxy10[label="b'X'y"];
b'X'y
661.41333
print 'model (6.11)';
x11 = col1 || col3 || col4;
xtx11 = t(x11)*x11;
xty11 = t(x11)*y;
b11 = inv(xtx11)*xty11;
print xtx11 xty11 b11[format=6.3];
model (6.11)
XTX11 XTY11 B11
12 4 4 88.2 6.200
4 4 0 28.6 0.950
4 0 4 34.8 2.500
bxy11 = t(b11)*xty11;
print bxy11[label="b'X'y"];
b'X'y
661.01
print 'model (6.12)';
x12 = col1 || col6;
xtx12 = t(x12)*x12;
xty12 = t(x12)*y;
b12 = inv(xtx12)*xty12;
print xtx12 xty12 b12[format=6.3];
model (6.12)
XTX12 XTY12 B12
12 6 88.2 7.533
6 6 43 -0.367
bxy12 = t(b12)*xty12;
print bxy12[label="b'X'y"];
b'X'y
648.67333
print 'mean only model';
xm = col1;
bm = inv(t(xm)*xm)*(t(xm)*y);
bxym = t(bm)*(t(xm)*y);
print bm bxym;
mean only model
BM BXYM
7.35 648.27
*table 6.10;
sds = t(y)*y - bxy;
sdi = t(y)*y - bxy10;
sdb = t(y)*y = bxy11;
sda = t(y)*y - bxy12;
sdm = t(y)*y - bxym;
print ' Table 6.10 Summary of calculations ';
print '-----------------------------------------------------------------------';
print ' Model ' 'd.f.' ' t(B)*t(X)*y ' ' Scaled Deviance';
print '-----------------------------------------------------------------------';
print 'mu+alpha+beta+alpha*beta' ' 6' bxy[label='' format=14.4]
' sigma2*D_S =' sds[label='' format=6.4];
print 'mu+alpha+beta ' ' 8' bxy10[label='' format=14.4]
' sigma2*D_I =' sdi[label='' format=6.4];
print 'mu+alpha ' ' 9' bxy11[label='' format=14.4]
' sigma2*D_B =' sdb[label='' format=6.4];
print 'mu+beta ' ' 10' bxy12[label='' format=14.4]
' sigma2*D_A =' sda[label='' format=6.4];
print 'mu ' ' 11' bxym[label='' format=14.4]
' sigma2*D_M =' sdm[label='' format=6.4];
quit;
Table 6.10 Summary of calculations
-----------------------------------------------------------------------
Model d.f. t(B)*t(X)*y Scaled Deviance
-----------------------------------------------------------------------
mu+alpha+beta+alpha*beta 6 662.6200 sigma2*D_S = 1.4800
mu+alpha+beta 8 661.4133 sigma2*D_I = 2.6867
mu+alpha 9 661.0100 sigma2*D_B = 0.0000
mu+beta 10 648.6733 sigma2*D_A = 15.427
mu 11 648.2700 sigma2*D_M = 15.830
Table 6.11 on page 105.
proc glm data = table6_9; class factora factorb; model data = factora|factorb /intercept ss3; run; quit;
Dependent Variable: data
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 6 662.6200000 110.4366667 447.72 <.0001
Error 6 1.4800000 0.2466667
Uncorrected Total 12 664.1000000
R-Square Coeff Var Root MSE data Mean
0.906507 6.757217 0.496655 7.350000
Source DF Type III SS Mean Square F Value Pr > F
Intercept 1 648.2700000 648.2700000 2628.12 <.0001
factorA 2 12.7400000 6.3700000 25.82 0.0011
factorB 1 0.4033333 0.4033333 1.64 0.2482
factorA*factorB 2 1.2066667 0.6033333 2.45 0.1672
Table 6.12 on page 106.
data table6_12;
input method $ y x;
cards;
A 6 3
A 4 1
A 5 3
A 3 1
A 4 2
A 3 1
A 6 4
B 8 4
B 9 5
B 7 5
B 9 4
B 8 3
B 5 1
B 7 2
C 6 3
C 7 2
C 7 2
C 7 3
C 8 4
C 5 1
C 7 4
;
run;
proc sql;
select sum(y) as sum_y, sum(x) as sum_x,
sum(y*y) as sum_y2, sum(x*x) as sum_x2,
sum(y*x) as sum_xy
from table6_12
group by method;
quit;
sum_y sum_x sum_y2 sum_x2 sum_xy
------------------------------------------------
31 15 147 41 75
53 24 413 96 191
47 19 321 59 132
Figure 6.1 on page 107. Some of the data points are on top of each other. So we jittered the data by adding some random noise.
data table6_12a;
set table6_12;
yjittered = y + .2*ranuni(1234);
xjittered = x + .1*ranuni(2345);
run;
goptions reset = all;
symbol1 v = circle c=black h=2;
symbol2 v = plus c=red h=2;
symbol3 v = P c=blue font=marker;
axis1 order = (2 to 10 by 2) minor = none label=(a=90 'Achievement score,y');
axis2 order = (0 to 6 by 1) minor = none label=('Initial aptitude, x') offset=(2,2);
proc gplot data = table6_12a;
plot yjittered*xjittered = method /vaxis = axis1 haxis=axis2;
run;
quit;
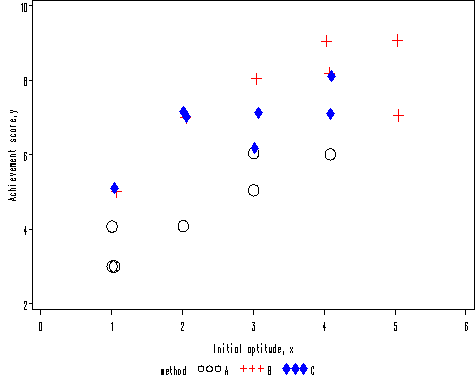
Table 6.13 on page 108.
proc glm data = table6_12; class method; model y = method x /intercept ss3; run; quit;
Dependent Variable: y
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 4 870.6979592 217.6744898 359.20 <.0001
Error 17 10.3020408 0.6060024
Uncorrected Total 21 881.0000000
R-Square Coeff Var Root MSE y Mean
0.838550 12.47915 0.778462 6.238095
Source DF Type III SS Mean Square F Value Pr > F
Intercept 1 58.05399323 58.05399323 95.80 <.0001
method 2 16.93200174 8.46600087 13.97 0.0003
x 1 16.55510204 16.55510204 27.32 <.0001
