Version info: Code for this page was tested in Mplus version 6.12.
Multinomial logistic regression is used to model nominal outcome variables, in which the log odds of the outcomes are modeled as a linear combination of the predictor variables.
Please note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and checking, verification of assumptions, model diagnostics and potential follow-up analyses.
Examples of multinomial logistic regression
Example 1. People’s occupational choices might be influenced by their parents’ occupations and their own education level. We can study the relationship of one’s occupation choice with education level and father’s occupation. The occupational choices will be the outcome variable which consists of categories of occupations.
Example 2. A biologist may be interested in food choices that alligators make. Adult alligators might have different preferences from young ones. The outcome variable here will be the types of food, and the predictor variables might be size of the alligators and other environmental variables.
Example 3. Entering high school students make program choices among general program, vocational program and academic program. Their choice might be modeled using their writing score and their social economic status.
Description of the data
For our data analysis example, we will expand our third example with a hypothetical data set. The data set contains variables on 200 students. The outcome variable is prog, program type, where program type 1 is general, type 2 is academic, and type 3 is vocational. The predictor variables are social economic status, ses, a three-level categorical variable and writing score, write, a continuous variable. Let’s start with getting some descriptive statistics of the variables of interest. You can download the data set here.
Data:
File is D:hsbdemo.dat ;
Variable:
Names are
id female ses schtyp prog read write math science socst honors awards
cid;
Missing are all (-9999) ;
Analysis:
Type = basic;
Plot:
type = plot1;
RESULTS FOR BASIC ANALYSIS
ESTIMATED SAMPLE STATISTICS
Means
ID FEMALE SES SCHTYP PROG
________ ________ ________ ________ ________
1 100.500 0.545 2.055 1.160 2.025
Means
READ WRITE MATH SCIENCE SOCST
________ ________ ________ ________ ________
1 52.230 52.775 52.645 51.850 52.405
Means
HONORS AWARDS CID
________ ________ ________
1 0.265 1.670 10.430
Covariances
ID FEMALE SES SCHTYP PROG
________ ________ ________ ________ ________
ID 3333.250
FEMALE -2.507 0.248
SES 8.797 -0.045 0.522
SCHTYP 10.210 0.003 0.036 0.134
PROG -2.308 0.001 0.009 -0.024 0.474
READ 87.755 -0.270 2.167 0.323 -0.951
WRITE 101.907 1.208 1.417 0.441 -1.179
MATH 118.283 -0.137 1.840 0.337 -0.966
SCIENCE 183.260 -0.628 2.018 0.234 -1.291
SOCST 113.333 0.279 2.568 0.380 -1.440
HONORS 1.148 0.031 0.060 -0.002 -0.012
AWARDS 10.490 0.160 0.318 0.038 -0.152
CID 89.335 0.031 1.336 0.236 -0.766
Covariances
READ WRITE MATH SCIENCE SOCST
________ ________ ________ ________ ________
READ 104.597
WRITE 57.707 89.394
MATH 63.297 54.555 87.329
SCIENCE 63.649 53.266 58.212 97.538
SOCST 68.067 61.236 54.489 49.191 114.681
HONORS 2.209 2.820 2.234 1.820 1.833
AWARDS 10.421 14.616 10.168 9.021 10.129
CID 50.576 44.807 46.073 47.645 40.461
Covariances
HONORS AWARDS CID
________ ________ ________
HONORS 0.195
AWARDS 0.652 3.291
CID 1.611 7.832 33.485
Correlations
ID FEMALE SES SCHTYP PROG
________ ________ ________ ________ ________
ID 1.000
FEMALE -0.087 1.000
SES 0.211 -0.125 1.000
SCHTYP 0.482 0.015 0.137 1.000
PROG -0.058 0.004 0.017 -0.095 1.000
READ 0.149 -0.053 0.293 0.086 -0.135
WRITE 0.187 0.256 0.207 0.127 -0.181
MATH 0.219 -0.029 0.272 0.098 -0.150
SCIENCE 0.321 -0.128 0.283 0.065 -0.190
SOCST 0.183 0.052 0.332 0.097 -0.195
HONORS 0.045 0.139 0.190 -0.015 -0.038
AWARDS 0.100 0.177 0.243 0.057 -0.121
CID 0.267 0.011 0.320 0.111 -0.192
Correlations
READ WRITE MATH SCIENCE SOCST
________ ________ ________ ________ ________
READ 1.000
WRITE 0.597 1.000
MATH 0.662 0.617 1.000
SCIENCE 0.630 0.570 0.631 1.000
SOCST 0.621 0.605 0.544 0.465 1.000
HONORS 0.489 0.676 0.542 0.418 0.388
AWARDS 0.562 0.852 0.600 0.503 0.521
CID 0.855 0.819 0.852 0.834 0.653
Correlations
HONORS AWARDS CID
________ ________ ________
HONORS 1.000
AWARDS 0.815 1.000
CID 0.631 0.746 1.000
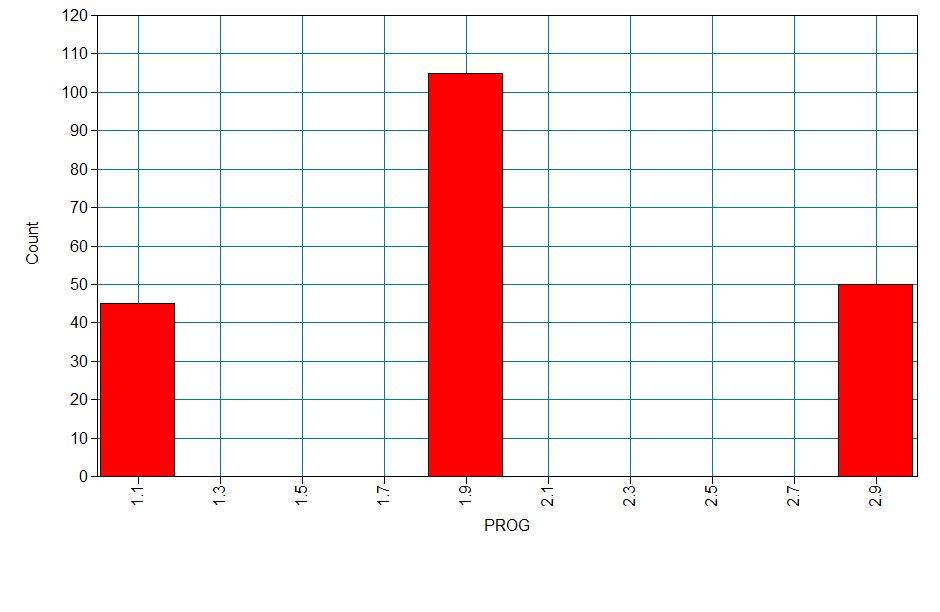
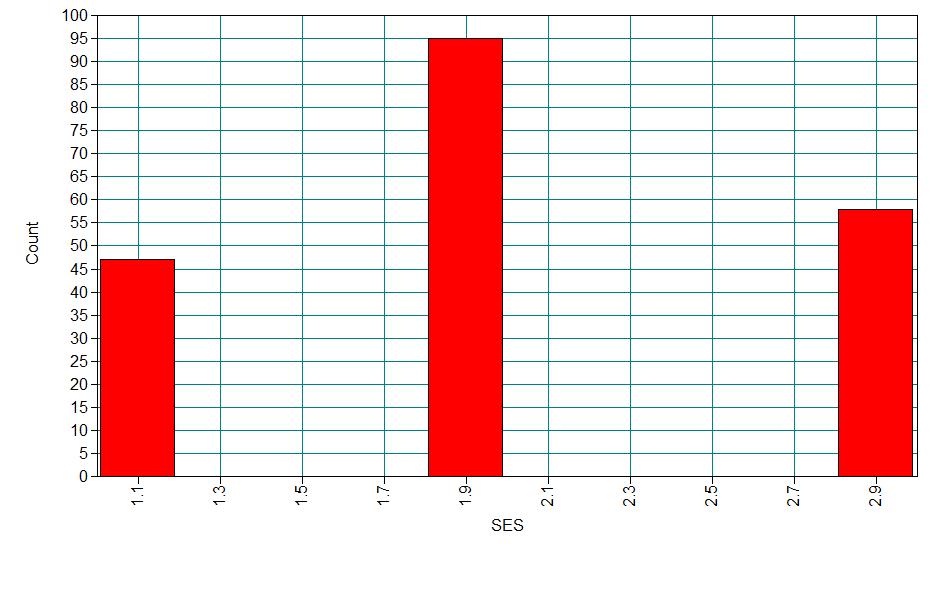
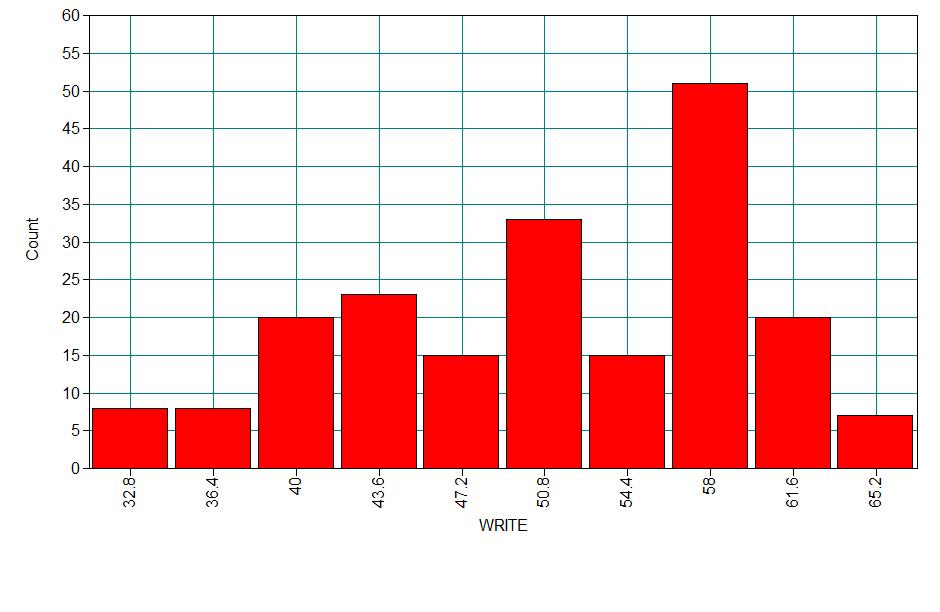
Analysis methods you might consider
- Multinomial logistic regression: the focus of this page.
- Multinomial probit regression: similar to multinomial logistic regression but with independent normal error terms.
- Multiple-group discriminant function analysis: A multivariate method for multinomial outcome variables
- Multiple logistic regression analyses, one for each pair of outcomes: One problem with this approach is that each analysis is potentially run on a different sample. The other problem is that without constraining the logistic models, we can end up with the probability of choosing all possible outcome categories greater than 1.
- Collapsing number of categories to two and then doing a logistic regression: This approach suffers from loss of information and changes the original research questions to very different ones.
- Ordinal logistic regression: If the outcome variable is truly ordered and if it also satisfies the assumption of proportional odds, then switching to ordinal logistic regression will make the model more parsimonious.
- Alternative-specific multinomial probit regression: allows different error structures therefore allows to relax the independence of irrelevant alternatives (IIA, see below “Things to Consider”) assumption. This requires that the data structure be choice-specific.
- Nested logit model: also relaxes the IIA assumption, also requires the data structure be choice-specific.
Multinomial logistic regression
Below we show how to regress prog on ses and write in a multinomial logit model in Mplus. We specify that the dependent variable, prog, is an unordered categorical variable using the Nominal option. Mplus will not automatically dummy-code categorical variables for you, so in order to get separate coefficients for ses groups 1 and 2 relative to ses group 3, we must create dummy variables using the Define command. We include our newly created dummy variables, ses1 and ses2, in both the Usevariables option and the Model command. In the multinomial logit model, one outcome group is used as the “reference group” (also called a base category), and the coefficients for all other outcome groups describe how the independent variables are related to the probability of being in that outcome group versus the reference group. Mplus automatically uses the last category of the dependent variable as the base category or comparison group, which in this case is the vocational category. Looking at the syntax below, in the model statement we have entered “prog#1 prog#2 on ses1 ses2 write.” Mplus uses a variable name followed by a pound sign and a number to refer to the categories of the nominal dependent variable, except the final category, which is the reference group and cannot be referred to in the model statement (if you try, Mplus will issue an error message). Thus the line included in our model statement indicates that we want to regress both levels of prog on ses(as dummy variables) and write. Additionally, by default for multinomial logistic regression, Mplus calculates robust standard errors.
Data:
File is C:UsersalinDocumentsmplus_andyhsbdemo.dat ;
Variable:
Names are
id female ses schtyp prog read write math science socst honors awards
cid;
Missing are all (-9999) ;
Usevariables are prog write ses1 ses2;
Nominal is prog;
Define:
ses1 = ses == 1;
ses2 = ses == 2;
Model:
prog#1 prog#2 on ses1 ses2 write;
MODEL FIT INFORMATION
Number of Free Parameters 8
Loglikelihood
H0 Value -179.982
H0 Scaling Correction Factor 1.016
for MLR
Information Criteria
Akaike (AIC) 375.963
Bayesian (BIC) 402.350
Sample-Size Adjusted BIC 377.005
(n* = (n + 2) / 24)
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
PROG#1 ON
SES1 0.180 0.651 0.277 0.782
SES2 -0.645 0.602 -1.071 0.284
WRITE 0.056 0.024 2.276 0.023
PROG#2 ON
SES1 -0.983 0.612 -1.604 0.109
SES2 -1.274 0.524 -2.430 0.015
WRITE 0.114 0.022 5.208 0.000
Intercepts
PROG#1 -2.546 1.331 -1.914 0.056
PROG#2 -4.236 1.206 -3.511 0.000
LOGISTIC REGRESSION ODDS RATIO RESULTS
PROG#1 ON
SES1 1.197
SES2 0.525
WRITE 1.057
PROG#2 ON
SES1 0.374
SES2 0.280
WRITE 1.120
- In the output above we see the final log likelihood (-179.982), which can be used in comparisons of nested models.
- Under the heading “Information Criteria” we see the Akaike and Bayesian information criterion values. Both the AIC and the BIC are measures of fit with some correction for the complexity of the model, but the BIC has a stronger correction for parsimony. In both cases, lower values indicate better fit of the model.
- The output above has two parts, labeled with the categories of the
outcome variable prog. They correspond to the two equations below:$$ln\left(\frac{P(prog=general)}{P(prog=vocational)}\right) = b_{10} + b_{11}(ses=1) + b_{12}(ses=2) + b_{13}write$$
$$ln\left(\frac{P(prog=academic)}{P(prog=vocational)}\right) = b_{20} + b_{21}(ses=1) + b_{22}(ses=2) + b_{23}write$$
where \(b\)’s are the regression coefficients.
- A one-unit increase in the variable write is associated with a 0.056 increase in the relative log odds of being in general program vs. vocational program .
- A one-unit increase in the variable write is associated with a 0.114 increase in the relative log odds of being in academic program vs. vocational program.
- The relative log odds of being in general program vs. in vocational program will decrease by 0.645 if moving from the highest level of ses (ses==3) to the middle level of ses (ses==2).
The ratio of the probability of choosing one outcome category over the probability of choosing the baseline category is often referred to as relative risk (and it is also sometimes referred to as odds as we have just used to described the regression parameters above). Relative risk can be obtained by exponentiating the linear equations above, yielding regression coefficients that are relative risk ratios for a unit change in the predictor variable. These relative risk ratios can be found in the Logistic Regression Odds Ratio Results section of the output.
- The relative risk ratio for a one-unit increase in the variable write is 1.057 (exp(0.056) from the Model Results output) for being in general program vs. vocational program.
- The relative risk ratio switching from ses = 3 to 1 is 1.197(exp(0.180) from the Model Results output) for being in general program vs. vocational program. In other words, the expected risk of staying in the general program is higher for subjects who are low in ses.
Things to consider
- The Independence of Irrelevant Alternatives (IIA) assumption: roughly, the IIA assumption means that adding or deleting alternative outcome categories does not affect the odds among the remaining outcomes.
- Diagnostics and model fit: unlike logistic regression where there are many statistics for performing model diagnostics, it is not as straightforward to do diagnostics with multinomial logistic regression models. For the purpose of detecting outliers or influential data points, one can run separate logit models and use the diagnostics tools on each model.
- Pseudo-R-Squared: the R-squared offered in the output is basically the change in terms of log-likelihood from the intercept-only model to the current model. It does not convey the same information as the R-square for linear regression, even though it is still “the higher, the better”.
- Sample size: multinomial regression uses a maximum likelihood estimation method, it requires a large sample size. It also uses multiple equations. This implies that it requires an even larger sample size than ordinal or binary logistic regression.
- Complete or quasi-complete separation: Complete separation implies that the outcome variable separates a predictor variable completely, leading to perfect prediction by the predictor variable. Perfect prediction means that only one value of a predictor variable is associated with only one value of the response variable. You can do a two-way tabulation of the outcome variable with the problematic variable to look for separation, and if detected, rerun the model without the problematic variable.
- Empty cells or small cells: You should check for empty or small cells by doing a cross-tabulation between categorical predictors and the outcome variable. If a cell has very few cases (a small cell), the model may become unstable or it might not even run at all.
See also
References
- Long, J. S. and Freese, J. (2006) Regression Models for Categorical and Limited Dependent Variables Using Stata, Second Edition. College Station, Texas: Stata Press.
- Hosmer, D. and Lemeshow, S. (2000) Applied Logistic Regression (Second Edition). New York: John Wiley & Sons, Inc..
- Agresti, A. (1996) An Introduction to Categorical Data Analysis. New York: John Wiley & Sons, Inc.
