Mplus Textbook
Examples
Solving Examples from EQS Manual Using Mplus
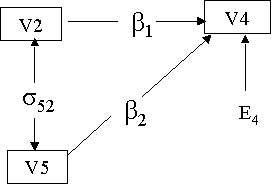
Example 1: A Simple Regression Model on page 15
The data file manul1.txt is the covariance matrix and can be downloaded here.
Title: Mplus code for example 1 from EQS manual on page 15
Data: File is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/manul1.txt;
Type is covariance ;
Nobservations = 932;
Variable: Names are y1 y2 y3 y4 y5 y6;
usevariables are y2 y4 y5;
Analysis: Type is general;
estimator is gls;
Model: y4 on y2 y5; !! Setting up the regression model;
y2 y5; !! Variance of y2 and y5 are free parameters to be
!! estimated;
MODEL RESULTS
Estimates S.E. Est./S.E.
Y4 ON
Y2 0.457 0.031 14.724
Y5 -0.192 0.031 -6.272
Y5 WITH
Y2 -3.889 0.336 -11.574
Variances
Y2 9.364 0.434 21.576
Y5 9.610 0.445 21.575
Residual Variances
Y4 6.991 0.324 21.575
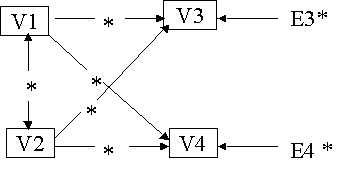
Example 2: A Two-Equation Path Model on page 22
The data file https://stats.idre.ucla.edu/wp-content/uploads/2016/02/manul1.txt used is the same as in previous example.
Title: Mplus code A Two-Equation Path Model on page 22
Data: File is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/manul1.txt;
Type is covariance ;
Nobservations = 932;
Variable: Names are y1 y2 y3 y4 y5 y6;
usevariables are y1 y2 y3 y4;
Analysis: Type is general;
estimator is ml;
Model: y3 on y1 y2;
y4 on y1 y2;
y1 y2;
y1 with y2;
MODEL RESULTS
Estimates S.E. Est./S.E.
Y3 ON
Y1 0.455 0.037 12.413
Y2 0.206 0.041 4.991
Y4 ON
Y1 0.158 0.034 4.660
Y2 0.420 0.038 11.048
Y1 WITH
Y2 6.939 0.413 16.815
Y4 WITH
Y3 4.277 0.289 14.802
Variances
Y1 11.821 0.548 21.587
Y2 9.354 0.433 21.587
Residual Variances
Y3 8.370 0.388 21.587
Y4 7.113 0.329 21.587
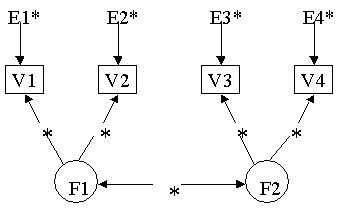
Example 3: A Factor Analysis Model on page 29
The data file https://stats.idre.ucla.edu/wp-content/uploads/2016/02/manul1.txt used is the same as in previous example.
Title: Mplus code: A Factor Analysis Model on page 29
Data: File is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/manul1.txt;
Type is covariance ;
Nobservations = 932;
Variable: Names are y1 y2 y3 y4 y5 y6;
usevariables are y1 y2 y3 y4;
Analysis: Type = general;
estimator is gls;
Model: f1 by y1* (1)
y2 (2);
f2 by y3* (1)
y4 (2);
f1@1 f2@1;
y1 y3 (3); !! setting the residual variance of
y2 y4 (4); !! y1 and y3 to be equal.
y1 with y3 (5); !! setting the residual covariance
y2 with y4 (5); !! of (y1, y3) equal to (y2, y4).
f1 with f2;
MODEL RESULTS
Estimates S.E. Est./S.E.
F1 BY
Y1 2.937 0.090 32.816
Y2 2.446 0.081 30.261
F2 BY
Y3 2.937 0.090 32.816
Y4 2.446 0.081 30.261
F1 WITH
F2 0.685 0.026 26.574
Y1 WITH
Y3 0.901 0.122 7.415
Y2 WITH
Y4 0.901 0.122 7.415
Variances
F1 1.000 0.000 0.000
F2 1.000 0.000 0.000
Residual Variances
Y1 3.519 0.267 13.176
Y2 3.644 0.206 17.717
Y3 3.519 0.267 13.176
Y4 3.644 0.206 17.717
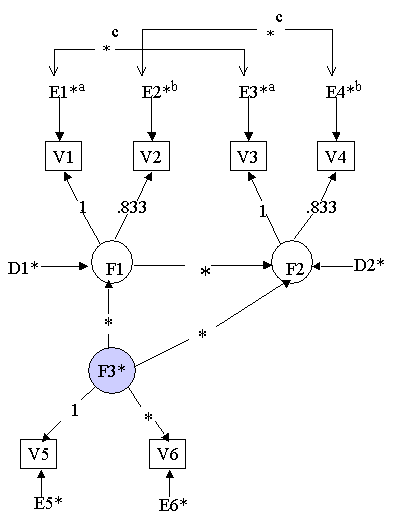
Example 4: A Complete Latent Variable Model on page 33
The data file https://stats.idre.ucla.edu/wp-content/uploads/2016/02/manul1.txt used is the same as in previous example.
Title: Mplus code: A COMPLETE LATENT VARIABLE MODEL
(EXAMPLE IN EQS MANUAL P.33)
Data: File is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/manul1.txt;
Type is covariance ;
Nobservations = 932;
Variable: Names are y1 y2 y3 y4 y5 y6;
Usevariables are y1 y2 y3 y4 y5 y6;
Analysis: Type = general;
estimator is ml;
Model: f1 by y1 y2@.833;
f2 by y3 y4@.833;
f3 by y5 y6;
f1 on f3;
f2 on f1 f3;
y1 y3 (3); !! setting the residual variance of
y2 y4 (4); !! y1 and y3 to be equal.
y1 with y3 (5); !! setting the residual covariance
y2 with y4 (5); !! of (y1, y3) equal to (y2, y4).
TESTS OF MODEL FIT
Chi-Square Test of Model Fit
Value 13.491
Degrees of Freedom 9
P-Value 0.1416
Chi-Square Test of Model Fit for the Baseline Model
Value 2133.653
Degrees of Freedom 15
P-Value 0.0000
CFI/TLI
CFI 0.998
TLI 0.996
Loglikelihood
H0 Value -13071.689
H1 Value -13064.944
Information Criteria
Number of Free Parameters 12
Akaike (AIC) 26167.379
Bayesian (BIC) 26225.427
Sample-Size Adjusted BIC 26187.316
(n* = (n + 2) / 24)
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.023
90 Percent C.I. 0.000 0.047
Probability RMSEA <= .05 0.971
SRMR (Standardized Root Mean Square Residual)
Value 0.015
MODEL RESULTS
Estimates S.E. Est./S.E.
F1 BY
Y1 1.000 0.000 0.000
Y2 0.833 0.000 0.000
F2 BY
Y3 1.000 0.000 0.000
Y4 0.833 0.000 0.000
F3 BY
Y5 1.000 0.000 0.000
Y6 0.537 0.043 12.385
F1 ON
F3 -0.630 0.056 -11.186
F2 ON
F1 0.593 0.047 12.685
F3 -0.241 0.055 -4.393
Y1 WITH
Y3 0.905 0.121 7.449
Y2 WITH
Y4 0.905 0.121 7.449
Variances
F3 6.609 0.638 10.357
Residual Variances
Y1 3.604 0.201 17.967
Y2 3.591 0.164 21.867
Y3 3.604 0.201 17.967
Y4 3.591 0.164 21.867
Y5 2.991 0.498 6.007
Y6 2.593 0.183 14.183
F1 5.664 0.422 13.413
F2 4.510 0.335 13.471
Example 5: A Second-order Factor Analysis Model on page 38
The data file https://stats.idre.ucla.edu/wp-content/uploads/2016/02/manul1.txt used is the same as in previous example.
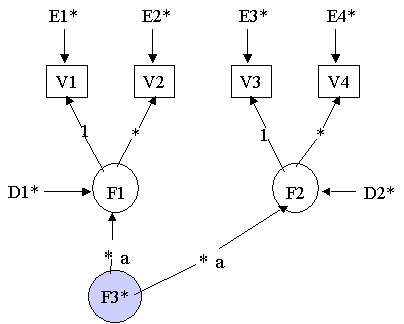
Title: Mplus code: A SECOND-ORDER FACTOR ANALYSIS MODEL
(EXAMPLE IN EQS MANUAL P.38)
Data: File is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/manul1.txt;
Type is covariance ;
Nobservations = 932;
Variable: Names are y1 y2 y3 y4 y5 y6;
usevariables are y1 y2 y3 y4 ;
Analysis: Type = general;
estimator is gls;
Model: f1 by y1 y2;
f2 by y3 y4;
f3 by f1@0 f1 f2 (1);
f3@1;
TESTS OF MODEL FIT
Chi-Square Test of Model Fit
Value 55.612
Degrees of Freedom 1
P-Value 0.0000
Chi-Square Test of Model Fit for the Baseline Model
Value 544.805
Degrees of Freedom 6
P-Value 0.0000
CFI/TLI
CFI 0.899
TLI 0.392
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.242
90 Percent C.I. 0.190 0.298
Probability RMSEA <= .05 0.000
SRMR (Standardized Root Mean Square Residual)
Value 0.032
MODEL RESULTS
Estimates S.E. Est./S.E.
F1 BY
Y1 1.000 0.000 0.000
Y2 0.847 0.042 20.158
F2 BY
Y3 1.000 0.000 0.000
Y4 0.815 0.040 20.343
F3 BY
F1 2.544 0.089 28.446
F1 2.544 0.089 28.446
F2 2.544 0.089 28.446
Variances
F3 1.000 0.000 0.000
Residual Variances
Y1 3.199 0.375 8.540
Y2 3.063 0.287 10.678
Y3 2.940 0.403 7.302
Y4 3.413 0.301 11.331
F1 1.976 0.438 4.514
F2 2.975 0.491 6.055
Example 6: A Nonstandard Model on page 104
The data file is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/bag.txt.
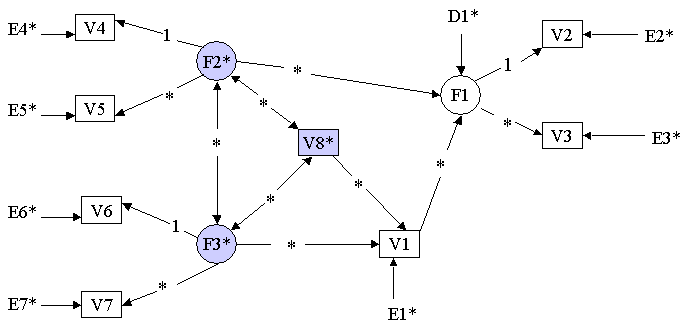
Title: Mplus code: Example 6: A Nonstandard Model on page 104
Data: File is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/bag.txt;
Type is correlation means stdeviations;
Nobservations = 122;
Variable: Names are y1 y2 y3 y4 y5 y6 y7 y8;
usevariables are y1 y2 y3 y4 y5 y6 y7 y8;
Analysis: Type = meanstructure;
estimator is ml;
Model: f1 by y2 y3*1;
f2 by y4 y5*1;
f3 by y6 y7*1;
y1 on f3 y8;
f1 on f2 y1;
f2 with f3;
y8 with f2;
y8 with f3;
MODEL RESULTS
Estimates S.E. Est./S.E.
F1 BY
Y2 1.000 0.000 0.000
Y3 0.763 0.131 5.807
F2 BY
Y4 1.000 0.000 0.000
Y5 1.234 0.398 3.096
F3 BY
Y6 1.000 0.000 0.000
Y7 0.874 0.142 6.173
F1 ON
F2 0.886 0.370 2.394
F1 ON
Y1 0.557 0.138 4.027
Y1 ON
F3 0.823 0.147 5.613
Y1 ON
Y8 -0.082 0.046 -1.761
F2 WITH
F3 0.692 0.299 2.314
Y8 WITH
F2 -1.412 0.569 -2.481
F3 -1.970 0.684 -2.878
Means
Y8 0.000 0.329 0.000
Intercepts
Y1 0.000 0.181 0.000
Y2 0.000 0.282 0.000
Y3 0.000 0.234 0.000
Y4 0.000 0.176 0.000
Y5 0.000 0.188 0.000
Y6 0.000 0.195 0.000
Y7 0.000 0.186 0.000
Variances
Y8 13.213 1.692 7.810
F2 1.234 0.528 2.338
F3 2.772 0.657 4.219
Residual Variances
Y1 2.099 0.377 5.570
Y2 3.815 1.285 2.968
Y3 3.257 0.808 4.030
Y4 2.537 0.506 5.011
Y5 2.413 0.660 3.655
Y6 1.855 0.440 4.216
Y7 2.091 0.391 5.351
F1 4.902 1.365 3.591
Example 7: A Simulated Confirmatory Factory Analysis Example on page 117
The data file used is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/data67.txt.
Title: Mplus code:
A Simulated Confirmatory Factory Analysis Example on page 117
Data: https://stats.idre.ucla.edu/wp-content/uploads/2016/02/data67.txt;
Variable: Names are y1 y2 y3 y4 y5 y6 ;
usevariables are y1 y2 y3 y4 y5 y6;
Analysis: Type = general;
estimator is ml;
Model: f1 by y1* y2 y3;
f2 by y4* y5 y6;
f1 with f2;
f1@1 f2@1;
MODEL RESULTS
Estimates S.E. Est./S.E.
F1 BY
Y1 1.541 0.348 4.430
Y2 0.481 0.164 2.929
Y3 0.186 0.181 1.028
F2 BY
Y4 0.663 0.154 4.294
Y5 0.871 0.162 5.364
Y6 0.180 0.140 1.284
F1 WITH
F2 0.638 0.169 3.768
Variances
F1 1.000 0.000 0.000
F2 1.000 0.000 0.000
Residual Variances
Y1 0.414 0.923 0.448
Y2 0.789 0.182 4.338
Y3 1.369 0.275 4.977
Y4 0.590 0.165 3.567
Y5 0.292 0.207 1.413
Y6 0.761 0.154 4.944
Example 8: 2 GROUP EXAMPLE FROM WERTS ET AL 1976 on page 158
The data file used for this example is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/page158.txt.
Title: Mplus code: EXAMPLE IN EQS MANUAL P. 158
Data: File is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/page158.txt;
Type is covariance ;
Nobservations = 865 900;
Ngroups = 2;
Variable: Names are y1 y2 y3 y4 ;
usevariables are y1 y2 y3 y4;
Analysis: Type = general;
estimator is ml;
Model: f1 by y1* y2;
f2 by y3* y4;
f1@1 f2@1;
f1 with f2 (1);
Model g2: f1 with f2 (1);
TESTS OF MODEL FIT
Chi-Square Test of Model Fit
Value 10.884
Degrees of Freedom 7
P-Value 0.1436
Chi-Square Test of Model Fit for the Baseline Model
Value 5478.850
Degrees of Freedom 12
P-Value 0.0000
CFI/TLI
CFI 0.999
TLI 0.999
Loglikelihood
H0 Value -21859.201
H1 Value -21853.759
Information Criteria
Number of Free Parameters 13
Akaike (AIC) 43744.403
Bayesian (BIC) 43815.590
Sample-Size Adjusted BIC 43774.290
(n* = (n + 2) / 24)
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.025
90 Percent C.I. 0.000 0.052
SRMR (Standardized Root Mean Square Residual)
Value 0.021
MODEL RESULTS
Estimates S.E. Est./S.E. Std StdYX
Group G1
F1 BY
Y1 7.438 0.155 47.881 7.438 0.938
Y2 9.676 0.199 48.623 9.676 0.909
F2 BY
Y3 7.283 0.152 48.003 7.283 0.920
Y4 5.192 0.114 45.507 5.192 0.902
F1 WITH
F2 0.767 0.012 62.183 0.767 0.767
Variances
F1 1.000 0.000 0.000 1.000 1.000
F2 1.000 0.000 0.000 1.000 1.000
Residual Variances
Y1 7.590 1.023 7.418 7.590 0.121
Y2 19.717 1.883 10.469 19.717 0.174
Y3 9.570 1.097 8.722 9.570 0.153
Y4 6.184 0.589 10.495 6.184 0.187
Group G2
F1 BY
Y1 7.438 0.155 47.881 7.438 0.897
Y2 9.676 0.199 48.623 9.676 0.944
F2 BY
Y3 7.283 0.152 48.003 7.283 0.931
Y4 5.192 0.114 45.507 5.192 0.884
F1 WITH
F2 0.767 0.012 62.183 0.767 0.767
Variances
F1 1.000 0.000 0.000 1.000 1.000
F2 1.000 0.000 0.000 1.000 1.000
Residual Variances
Y1 13.492 1.154 11.689 13.492 0.196
Y2 11.466 1.702 6.735 11.466 0.109
Y3 8.181 1.065 7.678 8.181 0.134
Y4 7.513 0.621 12.090 7.513 0.218
R-SQUARE
Group G1
Observed
Variable R-Square
Y1 0.879
Y2 0.826
Y3 0.847
Y4 0.813
Group G2
Observed
Variable R-Square
Y1 0.804
Y2 0.891
Y3 0.866
Y4 0.782
Example 9: Growth in Wisc Scores on page 175
The data file used for this example is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/manual9.txt.
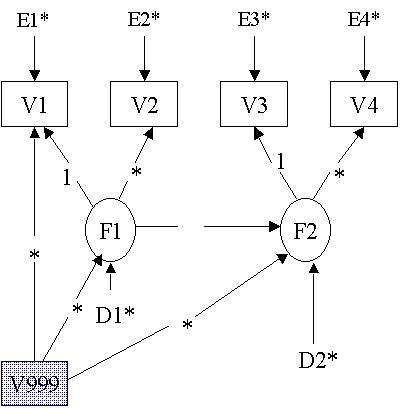
Example 10: Multiple Groups and Structured Means on page 186
The data file used for this example is https://stats.idre.ucla.edu/wp-content/uploads/2016/02/page186.txt.