Let’s look at an example. This example is based on example 5.1 from the Mplus User’s Guide. (Note: the Mplus User’s Guide, as well as all files needed to run the examples can be downloaded from the Mplus website.)
data: file is ex5.8.dat;
variable:
names are y1-y6 x1-x3;
usevariables are y1-y6;
model:
f1 by y1-y3;
f2 by y4-y6;
In the above confirmatory factor (or measurement) model we specify two latent variables f1 and f2, which are measured by the manifest variables y1-y3 and y4-y6 respectively. Our input file contains relatively little information about how the model should be structured, so Mplus will apply a number of defaults to our model when we run it.
By default, Mplus does the following:
- Sets the path loading from each factor to the first indicator variable listed after by in order to identify the model. In our example this means setting the path from y1 to be 1. It does the same for the path from f2 to y4. Note that the path between the latent variable and any of the manifest variables can be set to 1, it just happens that Mplus selects the first manifest variable listed by default. Also note that this is not the only way to identify a latent variable.
- Frees the variances of the errors of the manifest variables.
- Sets the covariances between the errors of the manifest variables to be zero, that is, it specifies no relationship between the manifest variables that is not accounted for by their relationship to the latent variable that predicts them and/or the correlation between that latent variable and the other variables in the model.
- Frees the intercepts of the manifest variables.
- Frees the variances of the latent variables (f1 and f2).
- Frees the covariance between the latent variables (f1 and f2) that is, it allows the latent variables to be correlated.
The figure below shows the model estimated by Mplus based on the input file above and Mplus defaults. Paths with a one ("1") next to them are constrained to one, paths with an asterisks are freely estimated. An asterisks next to a variable indicates that variables variance is estimated.
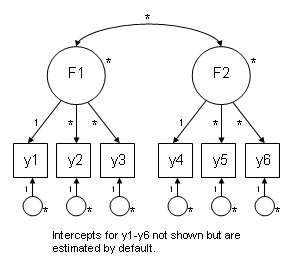
We can confirm these defaults by looking at the output Mplus produces. For example, under "F1 BY" we see that the factor loading for Y1 is 1.00, confirming that Mplus did fix the first factor loading to one. We can also see that the covariance between the two latent variables (under “F2 WITH”) is -0.030, with a standard error of 0.052, so we know that Mplus has estimated this as well.
<output omitted>
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
F1 BY
Y1 1.000 0.000 999.000 999.000
Y2 1.127 0.099 11.367 0.000
Y3 1.020 0.089 11.481 0.000
F2 BY
Y4 1.000 0.000 999.000 999.000
Y5 1.059 0.129 8.200 0.000
Y6 0.897 0.105 8.532 0.000
F2 WITH
F1 -0.030 0.052 -0.582 0.560
Intercepts
Y1 -0.022 0.063 -0.354 0.723
Y2 0.026 0.062 0.410 0.682
Y3 0.035 0.062 0.555 0.579
Y4 -0.022 0.064 -0.350 0.726
Y5 -0.016 0.058 -0.271 0.786
Y6 0.048 0.058 0.824 0.410
Variances
F1 0.907 0.125 7.253 0.000
F2 0.761 0.133 5.735 0.000
Residual Variances
Y1 1.064 0.096 11.120 0.000
Y2 0.798 0.100 7.971 0.000
Y3 1.010 0.095 10.597 0.000
Y4 1.290 0.119 10.869 0.000
Y5 0.854 0.111 7.712 0.000
Y6 1.067 0.097 11.026 0.000
