This seminar is a continuation of our Introduction to Mplus seminar. We will review the basics of Mplus syntax and show some examples for simple analyses, such as regression models for continuous and binary variables. Then we’ll move on to more advanced models, such as factor analysis, path analysis, growth curve models and latent class models. Some of the examples will be demonstrated by running Mplus in real time. The data files and the input files are zipped for an easy download and can be accessed by following the link.
Introduction
“We started to develop Mplus eleven years ago with the goal of providing applied researchers with powerful new statistical modeling techniques. We saw a wide gap between new statistical methods presented in the statistical literature and the statistical methods used by researchers in applied papers. Our goal was to help bridge this gap with easy-to-use but powerful software.” — February 2006, Preface to the Mplus User’s Guide.
Mplus has been very successful in achieving their goal and has been improving constantly ever since it was first released in 1998. Its general framework of continuous and categorical latent variables gives us a new framework to formulate statistical models. For example, not only we can perform growth curve analysis, but also latent class growth analysis; not only we can do discrete-time survival analysis, but also discrete-time survival mixture analysis. The possibilities of different ways of modeling make Mplus a very attractive piece of software. It offers several options to deal with the missing data issue, including maximum likelihood estimation and estimation based on the multiple imputed data sets.
Over the years, we have recommended to our clients the “get in and get out” approach with Mplus (and some other statistical packages) and it seems to us that this approach has worked well. This approach consists of a few steps: deciding the appropriate models for the study; deciding if switching to Mplus is necessary; preparing the data structure for Mplus using a familiar software package; and moving to Mplus and performing the analyses.
Our goal for this seminar is to help the transition process to Mplus. We will discuss the overall structure and syntax of Mplus input files. We will also discuss the usage of the Mplus 4 User’s Guide and the online resources for Mplus. Starting with some basic models, we will transit to some more advanced models.
Overall structure of Mplus input file
An input file defines the data set to use and the model to run. It is similar to a SAS program file, an SPSS syntax file and a Stata .do file. Below is an example of an input file. It is here to show the general structure of an input file. We are not going to explain what analysis it does.
Data:
File is d:workdatarawtable3_4.dat ;
Variable:
names are a b c d freq;
missing are all (-9999) ;
usevariables are a b c d;
weight is freq ; !default is frequency weight
categorical are a b c d;
classes = cl(2);
Analysis:
Type = mixture ;
starts = 0;
Model:
%overall%
[a$1*10 b$1*10 c$1*10 d$1*10] (1);
%cl#1%
[a$1*-10 b$1*-10 c$1*-10 d$1*-10] (2);
plot:
type= plot3;
series is a(1) b(2) c(3) d(4);
Here are some characteristics of an input file:
- an input line can not exceed 80 characters in width;
- variable names can not exceed 8 characters in length;
- only one model per input file;
- only one output file per input file;
- comments start with “!”;
- the default of the analysis type is type = general;
- the keywords categorical and count are for outcome variables only;
- new variables can be defined using the” define” command.
Here are some characteristics of a data file:
- must be in ASCII format;
- can be in fixed format or delimited;
- can be raw data or correlation data;
- no variable names in the first line;
- only numeric variables are allowed;
- use stata2mplus to convert a Stata data file to an ASCII data file and an Mplus input file.
Overall review of Mplus syntax for the model command
Mplus has made a great effort to make the syntax as simple as possible. Since there are so many analyses that Mplus can perform, the model command can still get really involved. We have compiled a short list here for commonly used keywords.
- “on” for regression (regress response variable “on” predictor variables);
- “by” for factors (measured “by” observed variables);
- “with” for covariance (correlated “with”);
- “[x]” for means or intercepts;
- “x” alone means the variance of x;
- “*” for starting values;
- “@” for fixed values;
- “|” for random effects;
- use (_number_) to constrain a set of parameters to be equal.
Use of User’s Guide and online resources
The Mplus User’s Guide is an excellent reference both for Mplus syntax and for types of models possible in Mplus. It has the flavor of learning by doing. Its organization is very different from other user guides, such as that of Stata, SAS or SPSS. Examples for basic models can be found in the first chapter, and more advanced models are divided into later chapters. The section on syntax is near the end. A very important feature is that almost all of the examples in the Guide are included with the software itself. If one sees an interesting example, one can always run the model to see the output and to modify the example to suit one’s own modeling need. An equally important feature is that each example in the book has a counterpart of Monte Carlo simulation. In fact, the Monte Carlo simulation has been used for generating most of the data sets used in the User’s Guide. The help system of Mplus has A SUMMARY OF THE Mplus LANGUAGE for a quick reference.
The Mplus website has tremendous resources, with a very active discussion group on many topics for serious modelers and the website has many examples one can download. One can get access to the entire User’s Guide in PDF format from Mplus’ website. One can search the entire Mplus User’s Guide for examples and commands. It is a great place to learn new modeling possibilities and to learn Mplus language as well.
Post estimation
Mplus has three commands for post estimation. The output command, the savedata command and the plot command. The output command is used for requesting types of output to be included in the output file. For example, we can request sample statistics to be displayed by using the option sampstat in the output command. The savedata command is used for creating an ASCII data file for further data analysis. The plot command is needed for requesting plots. Mplus offers many model related plots and the controls over the plots are easy to use.
Simple examples
We will review how some simple models are done in Mplus. We will start with linear regression and then discuss models with binary outcomes.
Example 1. Where is the output for intercept? (linear regression)
The code below is for a simple linear regression with the dependent variable write regressed on the predictor variables female and read. So we use the keyword on in the model statement.
Data:
File is hsb2.dat ;
Variable:
Names are
id female race ses schtyp prog read write math science socst;
Missing are all (-9999) ;
usevariables are female write read;
Model:
write on female read;
MODEL RESULTS
Estimates S.E. Est./S.E.
WRITE ON
FEMALE 5.487 1.007 5.451
READ 0.566 0.049 11.546
Residual Variances
WRITE 50.113 5.011 10.000
Notice that something is missing in the output. Yes, the intercept is missing. What does it mean? Be default, Mplus performs an analysis of covariance. To understand what it is doing, let’s perform this analysis manually in the fashion of covariance analysis. We create the covariance matrix for the variables write, female and read, and use this covariance matrix as the input for our analysis.
Title: example of using covariance matrix.
input data is an matrix:
89.8436
1.21369 .249221
57.9967 -.271709 105.123;
Data: file is cov.dat;
type is covariance;
nobservations = 200;
Variable: names are write female read;
Model: write on female read;
Estimates S.E. Est./S.E.
WRITE ON
FEMALE 5.487 1.007 5.451
READ 0.566 0.049 11.546
Residual Variances
WRITE 50.113 5.011 10.000
That shows that the analysis we did at the beginning of this example is just an analysis of covariance. In order to estimate the intercept, which is the expected mean holding values of predictor variables at zero, we need to tell Mplus that we are also interested in the analysis of means. This can be done easily by adding type = meanstructure to the analysis command. Every model has an analysis command associated with it. In this example, we don’t see the analysis command because we are using the default setting. The default setting is analysis: type = general. Models that can be estimated using type=general include regression analysis, path analysis, confirmatory factor analysis, structural equation modeling and growth curve modeling. Within any specific analysis setting, we can add more options, such as type = missing when the data set has missing values, and we don’t want to do listwise deletion. Or we can add type =meanstructure to have the mean or intercept displayed in the output window as we are going to do here.
Data:
File is hsb2.dat ;
Variable:
Names are
id female race ses schtyp prog read write math science socst;
Missing are all (-9999) ;
usevariables are female write read;
Analysis:
type=meanstructure;
Model:
write on female read;
Estimates S.E. Est./S.E.
WRITE ON
FEMALE 5.487 1.007 5.451
READ 0.566 0.049 11.546
Intercepts
WRITE 20.228 2.693 7.511
Residual Variances
WRITE 50.113 5.011 10.000
Example 2. Is it a probit or a logit regression? (binary outcome)
Now let’s switch to binary outcomes. Using the same data set as in previous example, we create a new dichotomous variable called hon based on the variable write. We also declare that the new variable hon is a categorical variable. As we have mentioned before, the keyword categorical is for outcome variables only. If we have categorical variables as predictors, we have to make sure the dummy variables have been created for them (usually in another software package before the data are moved into Mplus).
Data:
File is hsb2.dat ;
Variable:
Names are
id female race ses schtyp prog read write math science socst;
Missing are all (-9999) ;
usevariables are female math read hon;
categorical is hon;
define: hon = (write>60);
Model:
hon on female math read;
Observed dependent variables
Binary and ordered categorical (ordinal) HON
Observed independent variables FEMALE MATH READ
Estimator WLSMV Maximum number of iterations 1000 Convergence criterion 0.500D-04 Maximum number of steepest descent iterations 20 Parameterization DELTA
Input data file(s) hsb2.dat
Input data format FREE
SUMMARY OF CATEGORICAL DATA PROPORTIONS
HON
Category 1 0.755
Category 2 0.245
(output omitted...) MODEL RESULTS
Estimates S.E. Est./S.E.
HON ON
FEMALE 0.574 0.246 2.335
MATH 0.069 0.016 4.324
READ 0.038 0.017 2.275
R-SQUARE
Observed Residual
Variable Variance R-Square
HON 1.000 0.489
Now, is this a probit model or a logit model? Mplus is not very explicit about it. By default, it is a probit model. In case we don’t know the default, we can still tell that this is a probit model since it has an output section on R-square with residual variance of 1. This is what probit models assume. It assumes that the residual variance follows the standard normal distribution. Now did we miss something again? Yes. We don’t see the intercept. This is the exact same situation as we had with the linear regression. Adding type=meanstructure will give us the intercept, which Mplus calls “threshold”.
Data:
File is hsb2.dat ;
Variable:
Names are id female race ses schtyp prog
read write math science socst;
Missing are all (-9999) ;
Usevariables are female math read hon;
Categorical is hon;
Define: hon = (write>60);
Analysis: type=meanstructure;
Model:
hon on female math read;
MODEL RESULTS
Estimates S.E. Est./S.E.
HON ON
FEMALE 0.574 0.246 2.335
MATH 0.069 0.016 4.324
READ 0.038 0.017 2.275
Thresholds
HON$1 6.887 1.063 6.482
R-SQUARE
Observed Residual
Variable Variance R-Square
HON 1.000 0.489
What about a logistic regression with the same data? To do a logistic regression, we will change the estimation method from the default method of WLSMV to ML.
Data:
File is hsb2.dat ;
Variable:
Names are id female race ses schtyp prog
read write math science socst;
Missing are all (-9999) ;
Usevariables are female math read hon;
Categorical is hon;
Define: hon = (write>60);
Analysis: estimator = ml;
Model:
hon on female math read;
Estimator ML (output omitted...) Link LOGIT Cholesky OFF
Input data file(s) hsb2.dat Input data format FREE
SUMMARY OF CATEGORICAL DATA PROPORTIONS
HON
Category 1 0.755
Category 2 0.245
THE MODEL ESTIMATION TERMINATED NORMALLY
TESTS OF MODEL FIT
Loglikelihood
H0 Value -78.085
Information Criteria
Number of Free Parameters 4
Akaike (AIC) 164.170
Bayesian (BIC) 177.363
Sample-Size Adjusted BIC 164.690
(n* = (n + 2) / 24)
MODEL RESULTS
Estimates S.E. Est./S.E.
HON ON
FEMALE 0.980 0.422 2.324
MATH 0.123 0.031 3.931
READ 0.059 0.027 2.224
Thresholds
HON$1 11.770 1.711 6.880
LOGISTIC REGRESSION ODDS RATIO RESULTS
HON ON
FEMALE 2.664
MATH 1.131
READ 1.061
Advanced examples
Example 1. Exploratory factor analysis
Exploratory factor analysis has often been used to explore the variable structures. But most statistical software lacks the sophisticated techniques to deal with the missing value issue or binary variables. On the other hand, Mplus allows us to take care of both issues. Let’s start with a simple exploratory factor analysis. This example is taken from our Annotated SPSS Output Factor Analysis page. The data set has many variables, and we are only going to use item13 – item24, as they are all about instructors.
Data:
File is factor.dat ;
Variable:
Names are
facsex facethn facnat facrank employm salary yrsteach yrsut degree
sample remind nstud studrank studsex grade gpa satisfy religion psd
item13 item14 item15 item16 item17 item18 item19 item20 item21 item22
item23 item24 item25 item26 item27 item28 item29 item30 item31 item32
item33 item34 item35 item36 item37 item38 item39 item40 item41 item42
item43 item44 item45 item46 item47 item48 item49 item50 item51 item52
race sexism racism rpolicy casteman competen sensitiv cstatus;
Missing are all (-9999) ;
Usevariables are item13 - item24;
Analysis:
estimator = ml;
Type = efa 1 3 ;
INPUT READING TERMINATED NORMALLY
SUMMARY OF ANALYSIS
Number of groups 1 Number of observations 1428
Number of dependent variables 12 Number of independent variables 0 Number of continuous latent variables 0
Observed dependent variables
Continuous ITEM13 ITEM14 ITEM15 ITEM16 ITEM17 ITEM18 ITEM19 ITEM20 ITEM21 ITEM22 ITEM23 ITEM24
Estimator ML Information matrix EXPECTED Maximum number of iterations 1000 Convergence criterion 0.500D-04 Maximum number of steepest descent iterations 20
Input data file(s) factor.dat
Input data format FREE
RESULTS FOR EXPLORATORY FACTOR ANALYSIS
EIGENVALUES FOR SAMPLE CORRELATION MATRIX
1 2 3 4 5
________ ________ ________ ________ ________
1 6.073 1.223 0.735 0.648 0.572
EIGENVALUES FOR SAMPLE CORRELATION MATRIX
6 7 8 9 10
________ ________ ________ ________ ________
1 0.539 0.485 0.429 0.383 0.334
EIGENVALUES FOR SAMPLE CORRELATION MATRIX
11 12
________ ________
1 0.311 0.267
(output omitted...)
EXPLORATORY ANALYSIS WITH 3 FACTOR(S) :
CHI-SQUARE VALUE 147.541
DEGREES OF FREEDOM 33
PROBABILITY VALUE 0.0000
RMSEA (ROOT MEAN SQUARE ERROR OF APPROXIMATION) :
ESTIMATE (90 PERCENT C.I.) IS 0.049 ( 0.041 0.058)
PROBABILITY RMSEA LE 0.05 IS 0.540
ROOT MEAN SQUARE RESIDUAL IS 0.0175
VARIMAX ROTATED LOADINGS
1 2 3
________ ________ ________
ITEM13 0.744 0.158 0.236
ITEM14 0.753 0.197 0.213
ITEM15 0.650 0.303 0.258
ITEM16 0.581 0.292 0.177
ITEM17 0.532 0.468 0.300
ITEM18 0.277 0.731 0.240
ITEM19 0.158 0.745 0.130
ITEM20 0.243 0.470 0.187
ITEM21 0.350 0.504 0.383
ITEM22 0.189 0.531 0.319
ITEM23 0.409 0.365 0.724
ITEM24 0.321 0.309 0.604
PROMAX ROTATED LOADINGS
1 2 3
________ ________ ________
ITEM13 0.820 -0.098 0.050
ITEM14 0.828 -0.037 0.001
ITEM15 0.645 0.110 0.063
ITEM16 0.591 0.152 -0.029
ITEM17 0.424 0.342 0.105
ITEM18 0.035 0.790 0.009
ITEM19 -0.079 0.890 -0.116
ITEM20 0.093 0.475 0.032
ITEM21 0.144 0.402 0.268
ITEM22 -0.048 0.510 0.218
ITEM23 0.128 0.044 0.786
ITEM24 0.079 0.048 0.662
PROMAX FACTOR CORRELATIONS
1 2 3
________ ________ ________
1 1.000
2 0.611 1.000
3 0.658 0.685 1.000
ESTIMATED RESIDUAL VARIANCES
ITEM13 ITEM14 ITEM15 ITEM16 ITEM17
________ ________ ________ ________ ________
1 0.367 0.349 0.418 0.545 0.408
ESTIMATED RESIDUAL VARIANCES
ITEM18 ITEM19 ITEM20 ITEM21 ITEM22
________ ________ ________ ________ ________
1 0.331 0.404 0.685 0.477 0.581
ESTIMATED RESIDUAL VARIANCES
ITEM23 ITEM24
________ ________
1 0.176 0.436
Example 2. Exploratory factor analysis with binary variables
For the purpose of illustration, we dichotomized the variables item13-item24 from the previous example. We will do the same exploratory factor analysis again, but with the binary variables. Factor analysis with binary variables uses the tetrachoric correlation structure. It requires much larger sample size than the case for continuous variables.
Data:
File is cat_factor.dat ;
Variable:
Names are
item13 item14 item15 item16 item17 item18 item19 item20 item21 item22
item23 item24 cat_13 - cat_24;
Missing are all (-9999) ;
usevariables are cat_13 - cat_24;
categorical are cat_13 - cat_24;
Analysis:
Type = efa 1 3 ;
SUMMARY OF ANALYSIS
Number of groups 1 Number of observations 1428
Number of dependent variables 12 Number of independent variables 0 Number of continuous latent variables 0
Observed dependent variables
Binary and ordered categorical (ordinal) CAT_13 CAT_14 CAT_15 CAT_16 CAT_17 CAT_18 CAT_19 CAT_20 CAT_21 CAT_22 CAT_23 CAT_24
Estimator ULS Maximum number of iterations 1000 Convergence criterion 0.500D-04 Maximum number of steepest descent iterations 20
(output omitted...) RESULTS FOR EXPLORATORY FACTOR ANALYSIS
EIGENVALUES FOR SAMPLE CORRELATION MATRIX
1 2 3 4 5
________ ________ ________ ________ ________
1 7.208 1.280 0.768 0.622 0.451
EIGENVALUES FOR SAMPLE CORRELATION MATRIX
6 7 8 9
________ ________ ________ ________ ________
1 0.424 0.374 0.259 0.180 0.174
EIGENVALUES FOR SAMPLE CORRELATION MATRIX
11 12
________ ________
1 0.157 0.104
(output omitted...)
EXPLORATORY ANALYSIS WITH 3 FACTOR(S) :
ROOT MEAN SQUARE RESIDUAL IS 0.0199
VARIMAX ROTATED LOADINGS
1 2 3
________ ________ ________
CAT_13 0.813 0.260 0.297
CAT_14 0.806 0.228 0.306
CAT_15 0.824 0.293 0.262
CAT_16 0.758 0.307 0.141
CAT_17 0.724 0.502 0.226
CAT_18 0.254 0.794 0.241
CAT_19 0.363 0.728 0.154
CAT_20 0.223 0.484 0.153
CAT_21 0.271 0.574 0.414
CAT_22 0.177 0.592 0.320
CAT_23 0.412 0.413 0.812
CAT_24 0.337 0.368 0.613
PROMAX ROTATED LOADINGS
1 2 3
________ ________ ________
CAT_13 0.832 -0.005 0.120
CAT_14 0.832 -0.049 0.144
CAT_15 0.844 0.050 0.062
CAT_16 0.791 0.136 -0.087
CAT_17 0.657 0.369 -0.028
CAT_18 -0.032 0.882 0.008
CAT_19 0.151 0.799 -0.112
CAT_20 0.064 0.516 -0.003
CAT_21 0.017 0.517 0.300
CAT_22 -0.079 0.604 0.193
CAT_23 0.137 0.102 0.842
CAT_24 0.115 0.144 0.612
PROMAX FACTOR CORRELATIONS
1 2 3
________ ________ ________
1 1.000
2 0.606 1.000
3 0.574 0.645 1.000
ESTIMATED RESIDUAL VARIANCES
CAT_13 CAT_14 CAT_15 CAT_16 CAT_17
________ ________ ________ ________ ________
1 0.183 0.205 0.166 0.312 0.172
ESTIMATED RESIDUAL VARIANCES
CAT_18 CAT_19 CAT_20 CAT_21 CAT_22
________ ________ ________ ________ ________
1 0.247 0.315 0.693 0.426 0.516
ESTIMATED RESIDUAL VARIANCES
CAT_23 CAT_24
________ ________
1 0.001 0.376
Example 3. Exploratory factor analysis on continuous outcome variables with missing data
For the purpose of illustration again, we have created another version of the data set. This data set is basely on the data set in Example 1 in the section of Advanced Examples. We have created a lot of missing values, and the pattern of missing is completely random. For the same analysis, we will add the type = missing option to tell Mplus that the analysis will be done without deleting any cases. In general, Mplus offers ML estimation under the assumption of MCAR and MAR. From the output labeled as “PROPORTION OF DATA PRESENT”, we can see that many variables have a good amount of missing data.
Data:
File is factor_missing.dat ;
Variable:
Names are
item13 item14 item15 item16 item17 item18 item19 item20 item21 item22
item23 item24;
Missing are all (-9999) ;
Analysis:
Type = efa 1 3 missing;
INPUT READING TERMINATED NORMALLY
SUMMARY OF ANALYSIS
Number of groups 1 Number of observations 1428
Number of dependent variables 12 Number of independent variables 0 Number of continuous latent variables 0
Observed dependent variables
Continuous ITEM13 ITEM14 ITEM15 ITEM16 ITEM17 ITEM18 ITEM19 ITEM20 ITEM21 ITEM22 ITEM23 ITEM24
Estimator ML Information matrix OBSERVED Maximum number of iterations 1000 Convergence criterion 0.500D-04 Maximum number of steepest descent iterations 20
Input data file(s) factor_missing.dat
Input data format FREE
SUMMARY OF DATA
Number of patterns 940
COVARIANCE COVERAGE OF DATA
Minimum covariance coverage value 0.100
PROPORTION OF DATA PRESENT
Covariance Coverage
ITEM13 ITEM14 ITEM15 ITEM16 ITEM17
________ ________ ________ ________ ________
ITEM13 0.492
ITEM14 0.209 0.436
ITEM15 0.216 0.183 0.433
ITEM16 0.266 0.235 0.225 0.513
ITEM17 0.277 0.235 0.227 0.280 0.544
ITEM18 0.257 0.228 0.237 0.264 0.282
ITEM19 0.245 0.218 0.218 0.263 0.275
ITEM20 0.271 0.232 0.214 0.288 0.293
ITEM21 0.305 0.277 0.272 0.319 0.343
ITEM22 0.349 0.298 0.305 0.370 0.379
ITEM23 0.422 0.377 0.371 0.443 0.477
ITEM24 0.410 0.368 0.368 0.436 0.466
Covariance Coverage
ITEM18 ITEM19 ITEM20 ITEM21 ITEM22
________ ________ ________ ________ ________
ITEM18 0.520
ITEM19 0.258 0.508
ITEM20 0.272 0.272 0.533
ITEM21 0.327 0.318 0.333 0.625
ITEM22 0.370 0.361 0.382 0.438 0.704
ITEM23 0.449 0.440 0.453 0.543 0.606
ITEM24 0.431 0.428 0.451 0.539 0.590
Covariance Coverage
ITEM23 ITEM24
________ ________
ITEM23 0.867
ITEM24 0.732 0.848
RESULTS FOR EXPLORATORY FACTOR ANALYSIS
EIGENVALUES FOR SAMPLE CORRELATION MATRIX
1 2 3 4 5
________ ________ ________ ________ ________
1 6.043 1.257 0.736 0.658 0.627
EIGENVALUES FOR SAMPLE CORRELATION MATRIX
6 7 8 9 10
________ ________ ________ ________ ________
1 0.551 0.454 0.439 0.422 0.331
EIGENVALUES FOR SAMPLE CORRELATION MATRIX
11 12
________ ________
1 0.267 0.213
(output omitted...)
EXPLORATORY ANALYSIS WITH 3 FACTOR(S) :
CHI-SQUARE VALUE 90.822
DEGREES OF FREEDOM 33
PROBABILITY VALUE 0.0000
RMSEA (ROOT MEAN SQUARE ERROR OF APPROXIMATION) :
ESTIMATE (90 PERCENT C.I.) IS 0.035 ( 0.027 0.044)
PROBABILITY RMSEA LE 0.05 IS 0.998
ROOT MEAN SQUARE RESIDUAL IS 0.0286
VARIMAX ROTATED LOADINGS
1 2 3
________ ________ ________
ITEM13 0.789 0.168 0.151
ITEM14 0.742 0.216 0.176
ITEM15 0.598 0.347 0.312
ITEM16 0.549 0.176 0.345
ITEM17 0.535 0.264 0.483
ITEM18 0.233 0.231 0.750
ITEM19 0.142 0.183 0.700
ITEM20 0.278 0.151 0.510
ITEM21 0.337 0.362 0.546
ITEM22 0.169 0.310 0.520
ITEM23 0.358 0.768 0.392
ITEM24 0.315 0.554 0.348
PROMAX ROTATED LOADINGS
1 2 3
________ ________ ________
ITEM13 0.897 -0.041 -0.091
ITEM14 0.812 0.031 -0.066
ITEM15 0.540 0.203 0.101
ITEM16 0.526 -0.034 0.235
ITEM17 0.433 0.041 0.388
ITEM18 -0.025 -0.021 0.848
ITEM19 -0.109 -0.043 0.827
ITEM20 0.137 -0.055 0.546
ITEM21 0.127 0.210 0.484
ITEM22 -0.061 0.194 0.519
ITEM23 0.062 0.829 0.089
ITEM24 0.096 0.558 0.137
PROMAX FACTOR CORRELATIONS
1 2 3
________ ________ ________
1 1.000
2 0.628 1.000
3 0.614 0.686 1.000
ESTIMATED RESIDUAL VARIANCES
ITEM13 ITEM14 ITEM15 ITEM16 ITEM17
________ ________ ________ ________ ________
1 0.327 0.373 0.424 0.549 0.411
ESTIMATED RESIDUAL VARIANCES
ITEM18 ITEM19 ITEM20 ITEM21 ITEM22
________ ________ ________ ________ ________
1 0.329 0.456 0.639 0.457 0.605
ESTIMATED RESIDUAL VARIANCES
ITEM23 ITEM24
________ ________
1 0.128 0.473
Example 4. Path analysis with indirect and direct effects
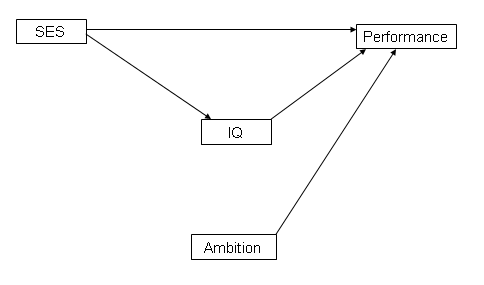
We have created a fake data set on school performance. We hypothesize that school performance will be related to student’s IQ, ambition and social economic status. On the other hand, student’s IQ might be also related to ses. Here is the diagram for our hypothesis:
Mplus offers a very straightforward way to display all the possible direct and indirect effects by using the model indirect statement.
Data:
File is path_anlaysis.dat ;
Variable:
Names are pfrm ses ambition iq;
Missing are all (-9999) ;
Model:
pfrm on iq ambition ses;
iq on ses;
Model indirect:
pfrm ind ses;
TESTS OF MODEL FIT
Chi-Square Test of Model Fit
Value 0.060
Degrees of Freedom 1
P-Value 0.8066
Chi-Square Test of Model Fit for the Baseline Model
Value 135.440
Degrees of Freedom 5
P-Value 0.0000
CFI/TLI
CFI 1.000
TLI 1.036
Loglikelihood
H0 Value -1775.747
H1 Value -1775.717
Information Criteria
Number of Free Parameters 6
Akaike (AIC) 3563.494
Bayesian (BIC) 3583.283
Sample-Size Adjusted BIC 3564.275
(n* = (n + 2) / 24)
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.000
90 Percent C.I. 0.000 0.117
Probability RMSEA <= .05 0.849
SRMR (Standardized Root Mean Square Residual)
Value 0.006
MODEL RESULTS
Estimates S.E. Est./S.E.
PFRM ON
IQ 0.547 0.051 10.728
AMBITION 5.635 1.009 5.584
SES 0.930 0.727 1.279
IQ ON
SES 4.152 0.957 4.339
Residual Variances
PFRM 49.706 4.971 10.000
IQ 95.599 9.560 10.000
TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Estimates S.E. Est./S.E.
Effects from SES to PFRM
Total 3.201 0.870 3.677
Total indirect 2.271 0.565 4.022
Specific indirect
PFRM
IQ
SES 2.271 0.565 4.022
Direct
PFRM
SES 0.930 0.727 1.279
Example 5. Growth curve modeling with the long format approach
We have chosen a simple example to show how Mplus can handle growth curve modeling. Unlike most statistical software, Mplus does growth curve modeling in both long and wide format. The two approaches offer different ways of looking at the same model and offer alternative models to one another. The example here is taken from Chapter 7 of Singer and Willett’s Applied Longitudinal Data Analysis. The outcome variable is the response time on a timed cognitive task called “opposites naming”. It is measured at four time points. We will start with the long format approach. This means that each subject will have potentially four rows of observations on the dependent variable and other covariates. In other words, this is the univariate approach. This is also the standard hierarchical linear model approach.
Data:
File is opposites_pp.dat;
Variable:
Names are
id time opp cog ccog wave;
Missing are all (-9999) ;
Usevariables are
time opp ccog;
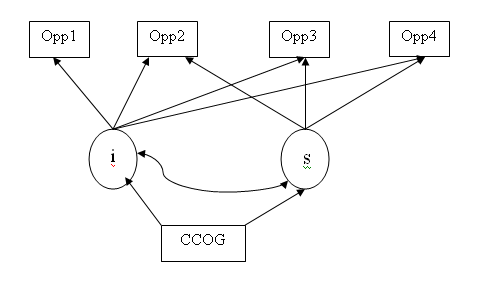
Cluster = id;
Within are time ;
Between are ccog;
Analysis: type = random twolevel;
Model:
%within%
s | opp on time;
%between%
opp s on ccog;
opp with s;
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 140
Number of dependent variables 1
Number of independent variables 2
Number of continuous latent variables 1
Observed dependent variables
Continuous
OPP
Observed independent variables
TIME CCOG
Continuous latent variables
S
Variables with special functions
Cluster variable ID
Within variables
TIME
Between variables
CCOG
Estimator MLR
Information matrix OBSERVED
Maximum number of iterations 1000
Convergence criterion 0.100D-05
Maximum number of EM iterations 500
Convergence criteria for the EM algorithm
Loglikelihood change 0.100D-02
Relative loglikelihood change 0.100D-05
Derivative 0.100D-02
Minimum variance 0.100D-03
Maximum number of steepest descent iterations 20
Maximum number of iterations for H1 2000
Convergence criterion for H1 0.100D-03
Optimization algorithm EMA
Input data file(s)
opposites_pp.dat
Input data format FREE
SUMMARY OF DATA
Number of clusters 35
Size (s) Cluster ID with Size s
4 1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
33 34 35
Average cluster size 4.000
Estimated Intraclass Correlations for the Y Variables
Intraclass Intraclass
Variable Correlation Variable Correlation
OPP 0.406
THE MODEL ESTIMATION TERMINATED NORMALLY
TESTS OF MODEL FIT
Loglikelihood
H0 Value -633.451
H0 Scaling Correction Factor 0.793
for MLR
Information Criteria
Number of Free Parameters 8
Akaike (AIC) 1282.901
Bayesian (BIC) 1306.434
Sample-Size Adjusted BIC 1281.123
(n* = (n + 2) / 24)
MODEL RESULTS
Estimates S.E. Est./S.E.
Within Level
Residual Variances
OPP 159.727 23.491 6.800
Between Level
S ON
CCOG 0.433 0.121 3.566
OPP ON
CCOG -0.114 0.416 -0.274
OPP WITH
S -165.185 67.783 -2.437
Intercepts
OPP 164.384 6.024 27.286
S 26.954 1.936 13.923
Residual Variances
OPP 1158.985 278.161 4.167
S 99.238 23.369 4.247
Example 6a. Growth curve modeling with the wide format approach
Now let’s move to growth curve modeling with a wide format approach. The data structure is now in wide format. That is each subject will only have one row of data, with four dependent variables corresponding to the four time points. In other words, this is the multivariate approach. To this end, we have to restructure the data from long to wide (in another statistical package). In order to match the results from the long format approach, we have to constrain the residual variance at each time point to be equal to each other. This also gives us a hint that the residual variances don’t have to be always equal, leading to more flexible models.
Data:
File is opposites_wide.dat ;
Variable:
Names are
id opp1 opp2 opp3 opp4 cog ccog;
Missing are all (-9999) ;
usev = opp1-opp4 ccog;
Analysis:
Type = meanstructure;
Model:
i s | opp1@0 opp2@1 opp3@2 opp4@3;
i s on ccog;
[i s];
[opp1-opp4@0]; ! constraining the mean to be zero at all time points.
opp1 - opp4 (1); ! constraining the residual variance to be equal
! at all time points.
INPUT READING TERMINATED NORMALLY
SUMMARY OF ANALYSIS
Number of groups 1 Number of observations 35
Number of dependent variables 4 Number of independent variables 1 Number of continuous latent variables 2
Observed dependent variables
Continuous OPP1 OPP2 OPP3 OPP4
Observed independent variables CCOG
Continuous latent variables I S
Estimator ML Information matrix EXPECTED Maximum number of iterations 1000 Convergence criterion 0.500D-04 Maximum number of steepest descent iterations 20
Input data file(s) opposites_wide.dat
Input data format FREE
THE MODEL ESTIMATION TERMINATED NORMALLY
TESTS OF MODEL FIT
Chi-Square Test of Model Fit
Value 6.899
Degrees of Freedom 10
P-Value 0.7350
Chi-Square Test of Model Fit for the Baseline Model
Value 134.996
Degrees of Freedom 10
P-Value 0.0000
CFI/TLI
CFI 1.000
TLI 1.025
Loglikelihood
H0 Value -770.987
H1 Value -767.538
Information Criteria
Number of Free Parameters 8
Akaike (AIC) 1557.975
Bayesian (BIC) 1570.418
Sample-Size Adjusted BIC 1545.438
(n* = (n + 2) / 24)
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.000
90 Percent C.I. 0.000 0.134
Probability RMSEA <= .05 0.787
SRMR (Standardized Root Mean Square Residual)
Value 0.043
MODEL RESULTS
Estimates S.E. Est./S.E.
I |
OPP1 1.000 0.000 0.000
OPP2 1.000 0.000 0.000
OPP3 1.000 0.000 0.000
OPP4 1.000 0.000 0.000
S |
OPP1 0.000 0.000 0.000
OPP2 1.000 0.000 0.000
OPP3 2.000 0.000 0.000
OPP4 3.000 0.000 0.000
I ON
CCOG -0.114 0.489 -0.232
S ON
CCOG 0.433 0.157 2.753
S WITH
I -165.303 78.279 -2.112
Intercepts
OPP1 0.000 0.000 0.000
OPP2 0.000 0.000 0.000
OPP3 0.000 0.000 0.000
OPP4 0.000 0.000 0.000
I 164.374 6.026 27.277
S 26.960 1.936 13.925
Residual Variances
OPP1 159.475 26.956 5.916
OPP2 159.475 26.956 5.916
OPP3 159.475 26.956 5.916
OPP4 159.475 26.956 5.916
I 1159.354 304.409 3.809
S 99.298 31.821 3.121
Example 6b. Growth curve modeling with the wide format approach (different parameterization)
As we have assumed in the previous models, the random intercept and the random slope are always correlated with each other. With the wide format approach, we can also model the correlation in the way of regression. This basically reparameterizes the model. But now we can describe the relationship between the intercept and the slope in terms of changes.
Data:
File is opposites_wide.dat ;
Variable:
Names are
id opp1 opp2 opp3 opp4 cog ccog;
Missing are all (-9999) ;
usev = opp1-opp4 ccog;
Analysis:
Type = meanstructure;
Model:
i s | opp1@0 opp2@1 opp3@2 opp4@3;
i s on ccog;
[i s];
s on i; ! different parameterization happens here
[opp1-opp4@0]; ! constraining the mean to be zero at all time points.
opp1 - opp4 (1); ! constraining the residual variance to be equal
! at all time points.
TESTS OF MODEL FIT
Chi-Square Test of Model Fit
Value 6.899
Degrees of Freedom 10
P-Value 0.7350
Chi-Square Test of Model Fit for the Baseline Model
Value 134.996
Degrees of Freedom 10
P-Value 0.0000
CFI/TLI
CFI 1.000
TLI 1.025
Loglikelihood
H0 Value -770.987
H1 Value -767.538
Information Criteria
Number of Free Parameters 8
Akaike (AIC) 1557.975
Bayesian (BIC) 1570.418
Sample-Size Adjusted BIC 1545.438
(n* = (n + 2) / 24)
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.000
90 Percent C.I. 0.000 0.134
Probability RMSEA <= .05 0.787
SRMR (Standardized Root Mean Square Residual)
Value 0.043
MODEL RESULTS
Estimates S.E. Est./S.E.
I |
OPP1 1.000 0.000 0.000
OPP2 1.000 0.000 0.000
OPP3 1.000 0.000 0.000
OPP4 1.000 0.000 0.000
S |
OPP1 0.000 0.000 0.000
OPP2 1.000 0.000 0.000
OPP3 2.000 0.000 0.000
OPP4 3.000 0.000 0.000
S ON
I -0.143 0.051 -2.773
I ON
CCOG -0.114 0.489 -0.232
S ON
CCOG 0.417 0.135 3.091
Intercepts
OPP1 0.000 0.000 0.000
OPP2 0.000 0.000 0.000
OPP3 0.000 0.000 0.000
OPP4 0.000 0.000 0.000
I 164.374 6.026 27.277
S 50.398 8.613 5.852
Residual Variances
OPP1 159.477 26.957 5.916
OPP2 159.477 26.957 5.916
OPP3 159.477 26.957 5.916
OPP4 159.477 26.957 5.916
I 1159.380 304.416 3.809
S 75.726 23.268 3.255
Example 7a. Latent class analysis
This example uses the hsb2 data set. We have test scores for the students in the sample and demographic variables as well. We want to see if we can classify students based on their test scores and how the class membership relates to other variables. This example is strictly for the purpose of illustration and therefore does not reflect any real theory or such. Notice that we have taken the default syntax to perform this analysis. We are looking for a two latent classes solution based on the scores on read, write, math, science and social studies (socst). The class membership is then regressed on the variables female and ses. Our model runs “successfully”. But Mplus gives us warning messages. It tells that the assumption that Mplus makes by default is that all the variables are uncorrelated within each latent class. Can we accept this assumption? Maybe not. But for the time being, let’s take a look at the rest of the output. We have the average scores for each of the two latent classes. We can tell that the first class has lower means on all the variables and the second one has higher means. These two classes make sense to us. Also, the class membership is highly related to ses.
Data:
File is hsb2.dat ;
Variable:
Names are
id female race ses schtyp prog read write math science socst;
Usevariables are
read write math science socst female ses;
classes = grp(2);
Analysis:
type=mixture;
Model:
%overall%
grp#1 on female ses;
*** WARNING in Model command
Variable is uncorrelated with all other variables within class: READ
*** WARNING in Model command
Variable is uncorrelated with all other variables within class: WRITE
*** WARNING in Model command
Variable is uncorrelated with all other variables within class: MATH
*** WARNING in Model command
Variable is uncorrelated with all other variables within class: SCIENCE
*** WARNING in Model command
Variable is uncorrelated with all other variables within class: SOCST
*** WARNING in Model command
All least one variable is uncorrelated with all other variables within class.
Check that this is what is intended.
6 WARNING(S) FOUND IN THE INPUT INSTRUCTIONS
Latent Class Analysis with Graphs
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 200
Number of dependent variables 5
Number of independent variables 2
Number of continuous latent variables 0
Number of categorical latent variables 1
Observed dependent variables
Continuous
READ WRITE MATH SCIENCE SOCST
Observed independent variables
FEMALE SES
Categorical latent variables
GRP
Estimator MLR
(output omitted...)
TESTS OF MODEL FIT
Loglikelihood
H0 Value -3510.499
H0 Scaling Correction Factor 1.126
for MLR
Information Criteria
Number of Free Parameters 18
Akaike (AIC) 7056.999
Bayesian (BIC) 7116.369
Sample-Size Adjusted BIC 7059.343
(n* = (n + 2) / 24)
Entropy 0.852
FINAL CLASS COUNTS AND PROPORTIONS FOR THE LATENT CLASSES
BASED ON THE ESTIMATED MODEL
Latent
Classes
1 96.61160 0.48306
2 103.38840 0.51694
FINAL CLASS COUNTS AND PROPORTIONS FOR THE LATENT CLASS PATTERNS
BASED ON ESTIMATED POSTERIOR PROBABILITIES
Latent
Classes
1 96.61161 0.48306
2 103.38839 0.51694
CLASSIFICATION OF INDIVIDUALS BASED ON THEIR MOST LIKELY LATENT CLASS MEMBERSHIP
Class Counts and Proportions
Latent
Classes
1 95 0.47500
2 105 0.52500
Average Latent Class Probabilities for Most Likely Latent Class Membership (Row)
by Latent Class (Column)
1 2
1 0.963 0.037
2 0.049 0.951
MODEL RESULTS
Estimates S.E. Est./S.E.
Latent Class 1
Means
READ 44.645 1.107 40.336
WRITE 45.822 1.197 38.269
MATH 45.766 0.806 56.784
SCIENCE 45.189 1.405 32.153
SOCST 45.785 1.375 33.288
Variances
READ 50.830 5.261 9.662
WRITE 44.222 5.109 8.656
MATH 43.108 4.842 8.903
SCIENCE 56.073 7.406 7.572
SOCST 73.733 7.395 9.970
Latent Class 2
Means
READ 59.318 1.168 50.791
WRITE 59.272 0.913 64.939
MATH 59.073 1.256 47.018
SCIENCE 58.075 0.836 69.495
SOCST 58.591 1.041 56.288
Variances
READ 50.830 5.261 9.662
WRITE 44.222 5.109 8.656
MATH 43.108 4.842 8.903
SCIENCE 56.073 7.406 7.572
SOCST 73.733 7.395 9.970
Categorical Latent Variables
GRP#1 ON
FEMALE -0.173 0.344 -0.502
SES -0.779 0.222 -3.506
Intercepts
GRP#1 1.622 0.556 2.917
LOGISTIC REGRESSION ODDS RATIO RESULTS
Categorical Latent Variables
GRP#1 ON
FEMALE 0.841
SES 0.459
ALTERNATIVE PARAMETERIZATIONS FOR THE CATEGORICAL LATENT VARIABLE REGRESSION
Parameterization using Reference Class 1
GRP#2 ON
FEMALE 0.173 0.344 0.502
SES 0.779 0.222 3.506
Intercepts
GRP#2 -1.622 0.556 -2.917
Example 7b. Latent class analysis with graphics
Now, let’s take up the issue of the correlation of variables within latent classes. We will also request some plots. Should we allow all the test scores to be correlated with each other? Maybe not. In this example, we allow reading scores to be correlated with all the other test scores, writing scores to be correlated with social studies scores, and math scores to be correlated with the science scores. We can take a look at the difference in AIC values and conclude that this is a better fitting model than the previous one.
Data:
File is hsb2.dat ;
Variable:
Names are
id female race ses schtyp prog read write math science socst;
Usevariables are
read write math science socst female ses;
classes = grp(2);
Analysis:
type=mixture;
Model:
%overall%
read with write;
read with math;
read with science;
read with socst;
write with socst;
math with science;
grp#1 on female ses;
Plot:
type is plot3;
series is read (1) write (2) math (3) science (4) socst (5);
(output omitted...)
TESTS OF MODEL FIT
Loglikelihood
H0 Value -3455.156
H0 Scaling Correction Factor 1.068
for MLR
Information Criteria
Number of Free Parameters 24
Akaike (AIC) 6958.313
Bayesian (BIC) 7037.472
Sample-Size Adjusted BIC 6961.438
(n* = (n + 2) / 24)
Entropy 0.838
FINAL CLASS COUNTS AND PROPORTIONS FOR THE LATENT CLASSES
BASED ON THE ESTIMATED MODEL
Latent
Classes
1 77.82126 0.38911
2 122.17874 0.61089
FINAL CLASS COUNTS AND PROPORTIONS FOR THE LATENT CLASS PATTERNS
BASED ON ESTIMATED POSTERIOR PROBABILITIES
Latent
Classes
1 77.82125 0.38911
2 122.17875 0.61089
CLASSIFICATION OF INDIVIDUALS BASED ON THEIR MOST LIKELY LATENT CLASS MEMBERSHIP
Class Counts and Proportions
Latent
Classes
1 76 0.38000
2 124 0.62000
Average Latent Class Probabilities for Most Likely Latent Class Membership (Row)
by Latent Class (Column)
1 2
1 0.956 0.044
2 0.042 0.958
MODEL RESULTS
Estimates S.E. Est./S.E.
Latent Class 1
READ WITH
WRITE 9.024 3.276 2.755
MATH 24.570 5.285 4.649
SCIENCE 27.390 5.820 4.706
SOCST 25.783 5.457 4.724
WRITE WITH
SOCST 18.927 3.559 5.319
MATH WITH
SCIENCE 27.609 6.718 4.109
Means
READ 45.417 0.942 48.209
WRITE 42.995 1.347 31.917
MATH 45.527 0.722 63.091
SCIENCE 45.100 1.172 38.487
SOCST 45.613 1.261 36.185
Variances
READ 66.360 5.860 11.324
WRITE 28.467 4.359 6.530
MATH 55.061 6.780 8.121
SCIENCE 68.513 9.495 7.216
SOCST 85.301 8.522 10.010
Latent Class 2
READ WITH
WRITE 9.024 3.276 2.755
MATH 24.570 5.285 4.649
SCIENCE 27.390 5.820 4.706
SOCST 25.783 5.457 4.724
WRITE WITH
SOCST 18.927 3.559 5.319
MATH WITH
SCIENCE 27.609 6.718 4.109
Means
READ 56.570 1.153 49.054
WRITE 59.005 0.580 101.768
MATH 57.179 1.072 53.347
SCIENCE 56.150 1.018 55.171
SOCST 56.731 1.024 55.428
Variances
READ 66.360 5.860 11.324
WRITE 28.467 4.359 6.530
MATH 55.061 6.780 8.121
SCIENCE 68.513 9.495 7.216
SOCST 85.301 8.522 10.010
Categorical Latent Variables
GRP#1 ON
FEMALE -1.166 0.419 -2.780
SES -1.069 0.278 -3.842
Intercepts
GRP#1 2.297 0.665 3.456
LOGISTIC REGRESSION ODDS RATIO RESULTS
Categorical Latent Variables
GRP#1 ON
FEMALE 0.312
SES 0.343
ALTERNATIVE PARAMETERIZATIONS FOR THE CATEGORICAL LATENT VARIABLE REGRESSION
Parameterization using Reference Class 1
GRP#2 ON
FEMALE 1.166 0.419 2.780
SES 1.069 0.278 3.842
Intercepts
GRP#2 -2.297 0.665 -3.456