Please note that this workshop is not intended to provide an introduction to the use of Mplus. Rather, it is assumed that you already have a basic familiarity with the software. If you need an introduction to Mplus, or if you would like to review the use of Mplus, please see our Introduction to Mplus seminar page and video.
In this workshop, we will cover only some of what can be done when running mediation models in Mplus. Much of the material in this workshop is based on Introduction to Mediation, Moderation and Conditional Process Analysis: A Regression-based Approach, Third Edition by Andrew F. Hayes (2022). The Mplus code for most of the models shown in this text is given on this website: https://www.figureitout.org.uk/mplusmedmod.htm . We will focus on mediation models; we will not cover moderation in any way. We will be using Mplus version 8.10. The PowerPoint slides are here: Introduction to Mediation Analysis using Mplus.
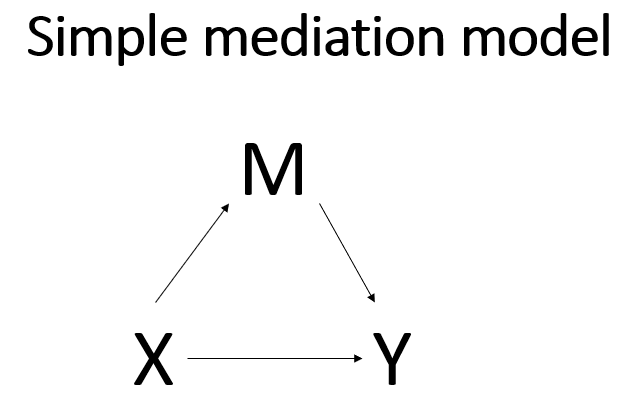
Simple mediation model with continuous predictor
Like so much in statistics, the basics of mediation models depend on a good understanding of linear (OLS) regression. In a simple linear regression, we would have one continuous outcome and one predictor, perhaps a binary predictor or maybe a continuous predictor. The difference between a simple linear regression and a simple mediation analysis is the inclusion of a single mediator to the model. Mathematically, the mediator acts like a covariate in the model. But conceptually, the mediator changes the simple regression model from a model that looks at the association of two variables to a model that tries to look at a causal relationship. Here is a conceptual diagram of a simple linear regression model:
We will assume that everyone is familiar linear regression.
In this model, we assume that there is a relationship between the predictor variable X and the outcome variable Y. The relationship may be correlational or causal or something else. There is no way to know the nature of the relationship from just the statistical model. The understanding of the relationship between X and Y comes from a thorough understanding of how the data were collected. In a simple mediation model, a third variable, called the mediator, M, is included in the model between X and Y.
The idea is that X now has two ways to influence Y. One way is direct, as in the simple regression model shown above. The second way is through M, the mediator. This is called the indirect effect. Of course, there is much more to mediation analysis than merely adding a variable to a regression model, and we will discuss some of those issues in this workshop. Because simple mediation analysis is based on linear regression, you can obtain much of the necessary output from a simple mediation analysis using a linear regression routine in your favorite statistical software program. However, other necessary parts of the output from a simple mediation analysis are difficult to get from regular regression output, so other routines, such as structural equation modeling (SEM), are used.
We will start off with the mechanics of how to run a simple mediation model, including the Mplus syntax. We will then discuss models that have more than one mediator.Finally, we will discuss assumptions that we must test or explore in order to claim a causal relationship between the variables in the model.
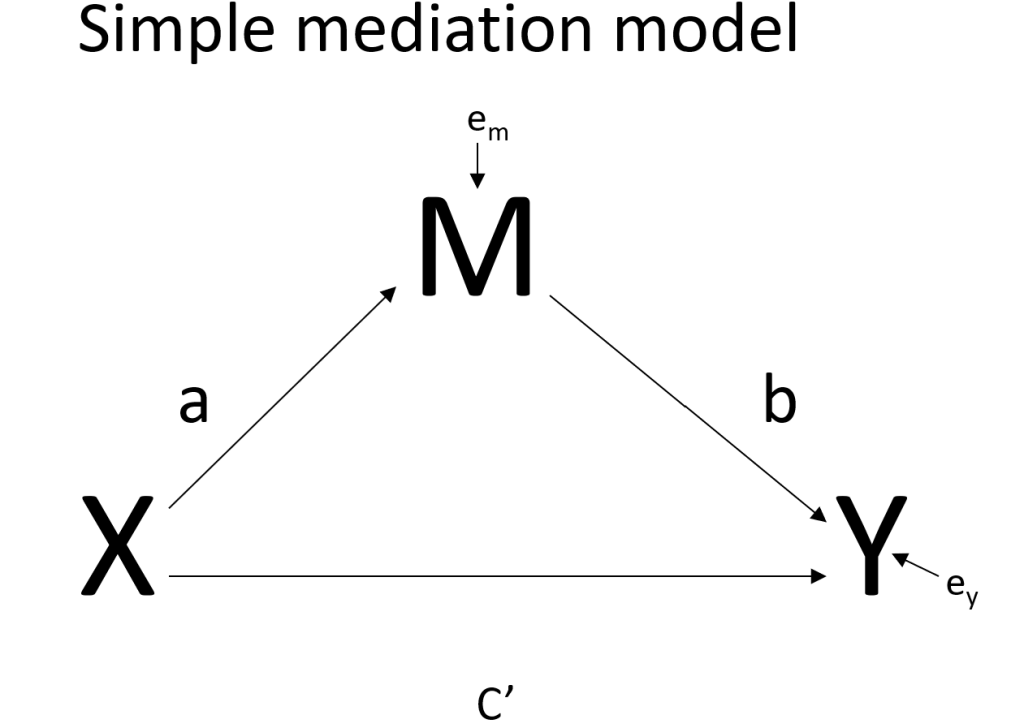
Let’s start with the simplest mediation model. This model has three continuous variables. Like a linear regression model, there is a predictor variable and an outcome variable. To make it a mediation model, we will add the mediator variable between the predictor and the outcome. The predictor variable (X) can be called the antecedent variable, because it occurs before either the mediator (M) or the outcome (Y). The outcome can be called the consequent variable, because it is believed to the consequence of the process the model describes. The mediator variable is both an antecedent variable (to the outcome) and a consequent variable (to the predictor).
The path from X to M is called a; the path from M to Y is called b; the path from X to Y is called c’. The indirect effect of X on Y through M is obtained by multiplying a and b. The total effect is the sum of the direct effect and the indirect effect. In other words, the total effect (called c) is (a * b) + c’. The fact that the indirect effect is obtained by multiplication has implications regarding the calculation of the standard error for this term.
For most of the tests given in the output of a mediation analysis, the normal theory approach is used. This approach makes some assumptions, and these assumptions are reasonable for these tests. However, there are at least two reasons to be concerned about using normal theory with indirect effects. First, it is known that the sampling distribution of a product term is (usually) not normal. Second, this approach may be lower in power than other approaches. There are several possible solutions for this, but the most commonly used solution is to calculate the confidence interval via bootstrap.
The diagram above is typically shown, but the diagram below is a little more accurate because it shows which variables have error terms associated with them.
Mplus can run mediation models when all of the variables are continuous, which is the simplest situation. Mplus can also run mediation models when the mediator and/or outcome are not continuous (e.g., binary, ordinal, nominal, count, etc.). The predictor may be continuous, binary or have multiple categories. In our first examples, all of the variables in our simple mediation model will be continuous. We will use the intro_mediation data. This is a simulated dataset that contains 5000 observations from a fictional study. In this fictional study, the researchers randomly assigned participants to receive information about careers in science. The amount of detail given to participants ranged from a little to quite a lot along a continuous scale. The variable is called detail in the dataset and is the predictor, or X, in all examples. The mediator (M) was the amount of experience, measured in hours, that the participants then had with science, such as working as an intern in a science lab, judging a science fair, tutoring students in science, etc. This variable is called exper in the dataset. The outcome (Y) was a measure of opinion regarding careers in science, called opinion in the dataset.
If you want to run the model as two regressions, you could use the syntax below. Not all of the output is shown for the sake of brevity.
title: regression of MV on IV
data: file is intro_mediation.dat;
variable: names are detail exper impact opinion ccovar bcovar;
usevariables = exper detail;
model: exper on detail;
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
EXPER ON
DETAIL 0.614 0.015 40.588 0.000
Intercepts
EXPER 80.964 1.262 64.169 0.000
Residual Variances
EXPER 102.673 2.053 50.000 0.000
title: regression of DV on IV and mediator
data: file is intro_mediation.dat;
variable: names are detail exper impact opinion ccovar bcovar;
usevariables = exper opinion detail;
model: opinion on detail exper;
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
DETAIL 1.011 0.019 51.976 0.000
EXPER 0.314 0.016 19.901 0.000
Intercepts
OPINION 101.915 1.901 53.611 0.000
Residual Variances
OPINION 127.809 2.556 50.000 0.000
This output is nice, but the indirect effect of detail on opinion via exper is not included, and neither is the total effect (which is the indirect effect plus the direct effect). For this reason, mediation models are rarely run as a series of regression models. Instead, the mediation model is run as a single model. In Mplus, there are two ways of getting the indirect and total effect. One way is to use the Model Constraint command, and the other is to use the Model Indirect command. Our first example will show the use of the Model Constraint command, and then we will look at an example using the Model Indirect command.
title: simple mediation model - all continuous variables with model constraint
! predictor variable - x: detail
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable: names are detail exper impact opinion ccovar bcovar;
usevariables = detail exper opinion;
analysis: type = general;
estimator = ml;
! in model statement, name each path using parentheses
model:
opinion on exper (b1);
opinion on detail (cdash); ! Direct effect of x on y
exper on detail (a1);
! use model constraint to calculate indirect and total effect
model constraint:
new(a1b1 total);
a1b1 = a1*b1; ! Indirect effect of x on y via m
total = a1*b1 + cdash; ! Total effect of x on y
Mplus VERSION 8.10
MUTHEN & MUTHEN
INPUT INSTRUCTIONS
title: simple mediation model - all continuous variables with model constraint
! predictor variable - x: detail
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable: names are detail exper impact opinion ccovar bcovar;
usevariables = detail exper opinion;
analysis: type = general;
estimator = ml;
! in model statement, name each path using parentheses
model:
opinion on exper (b1);
opinion on detail (cdash); ! Direct effect of x on y
exper on detail (a1);
! use model constraint to calculate indirect and total effect
model constraint:
new(a1b1 total);
a1b1 = a1*b1; ! Indirect effect of x on y via m
total = a1*b1 + cdash; ! Total effect of x on y
INPUT READING TERMINATED NORMALLY
simple mediation model - all continuous variables with model constraint
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 5000
Number of dependent variables 2
Number of independent variables 1
Number of continuous latent variables 0
Observed dependent variables
Continuous
EXPER OPINION
Observed independent variables
DETAIL
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 1000
Convergence criterion 0.500D-04
Maximum number of steepest descent iterations 20
Input data file(s)
intro_mediation.dat
Input data format FREE
UNIVARIATE SAMPLE STATISTICS
UNIVARIATE HIGHER-ORDER MOMENT DESCRIPTIVE STATISTICS
Variable/ Mean/ Skewness/ Minimum/ % with Percentiles
Sample Size Variance Kurtosis Maximum Min/Max 20%/60% 40%/80% Median
EXPER 131.845 0.034 86.303 0.02% 122.126 128.683 131.802
5000.000 136.500 -0.007 176.176 0.02% 134.746 141.553
OPINION 227.135 0.052 167.442 0.02% 213.095 222.728 227.098
5000.000 268.076 0.010 282.136 0.02% 231.195 240.820
DETAIL 82.884 -0.015 49.943 0.02% 74.894 80.601 82.934
5000.000 89.769 0.041 116.473 0.02% 85.382 90.652
THE MODEL ESTIMATION TERMINATED NORMALLY
MODEL FIT INFORMATION
Number of Free Parameters 7
Loglikelihood
H0 Value -37894.587
H1 Value -37894.587
Information Criteria
Akaike (AIC) 75803.174
Bayesian (BIC) 75848.794
Sample-Size Adjusted BIC 75826.551
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit
Value 0.000
Degrees of Freedom 0
P-Value 0.0000
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.000
90 Percent C.I. 0.000 0.000
Probability RMSEA <= .05 0.000
CFI/TLI
CFI 1.000
TLI 1.000
Chi-Square Test of Model Fit for the Baseline Model
Value 5127.598
Degrees of Freedom 3
P-Value 0.0000
SRMR (Standardized Root Mean Square Residual)
Value 0.000
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
EXPER 0.314 0.016 19.901 0.000
DETAIL 1.011 0.019 51.976 0.000
EXPER ON
DETAIL 0.614 0.015 40.588 0.000
Intercepts
EXPER 80.964 1.262 64.169 0.000
OPINION 101.915 1.901 53.611 0.000
Residual Variances
EXPER 102.672 2.053 50.000 0.000
OPINION 127.810 2.556 50.000 0.000
New/Additional Parameters
A1B1 0.193 0.011 17.868 0.000
TOTAL 1.204 0.018 68.685 0.000
QUALITY OF NUMERICAL RESULTS
Condition Number for the Information Matrix 0.947E-06
(ratio of smallest to largest eigenvalue)
DIAGRAM INFORMATION
Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram.
If running Mplus from the Mplus Diagrammer, the diagram opens automatically.
This will be one of the few times we show all of the output because there is so much output. The syntax that was submitted is echoed in the output. After that, you should see the statement “Input reading terminated normally.” This is a good sign, but you should always check the number of observations to ensure that it is correct. The number of groups should be 1 because we are not doing a multi-group analysis. The number of dependent variables should be two because both the mediator (in our example, exper) and the ultimate outcome (in our example, opinion) are outcomes. There are two observed dependent variables, one observed independent variable, and no latent variables. The default estimator is ML, which is fine. If your sample size is small, you may wish to use MLR.
The section titled “Univariate higher-order moment descriptive statistics” should be reviewed at least once for each dataset. These values should match what you would get from your preferred general-use statistical software package (assuming no missing data).
The statement “Model estimation terminated normally” is a good sign. It does not guarantee that there were no problems with the model, but you should be concerned if you do not see it.
In the section titled “Model fit information”, you will see the number of free parameters. For this model, we have seven free parameters. We will discuss what those are when we get to that part of the output. Next we have the likelihood value and the information criteria. These are not needed unless models are being compared. The model fit tests are uninformative for this model (because this is a saturated model), and so they are not interpreted and would not be reported.
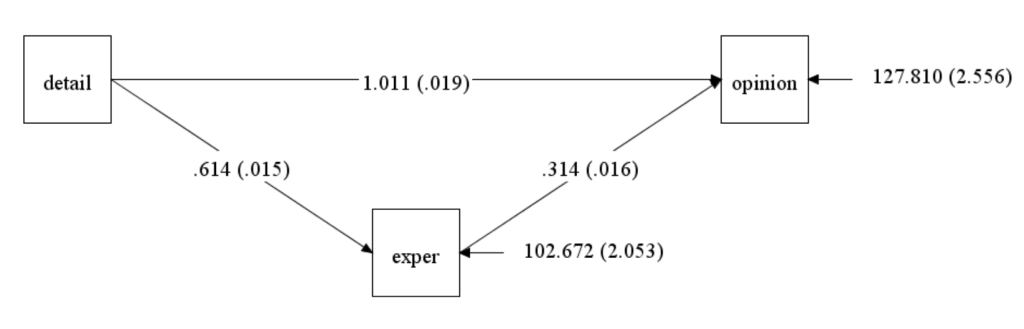
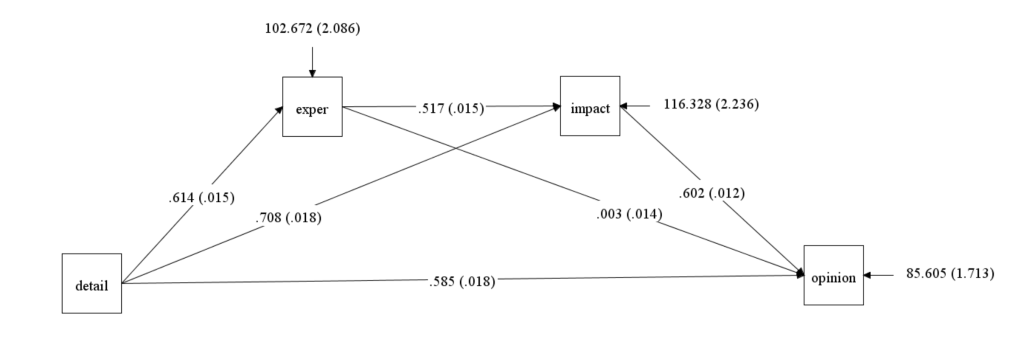
The next section of the output is titled “Model results”, and this is the part we will report and interpret. We see the three regression coefficients, their standard errors, the estimate divided by the standard error (“Est./S.E.”), and the two-tailed p-value. We also have the intercepts for the two models, but we do not need to do anything with these. The residual variances for the two outcomes are given next. If we look at the diagram produced by Mplus, we will see these values (except for the intercepts), along with the standard errors. In general, including the path diagram in a presentation or paper for publication is a good idea. At the very least, you, as the analyst, should look at the diagram to ensure that it looks like you expect. You should ensure that all of the values that you expected to be estimated were estimated, and likewise, ensure that no other values were estimated. If the diagram produced by Mplus does not match what you were expecting, you need to update your Mplus syntax and rerun the model.
In the section titled “New/additional parameters”, you will see the estimates for the new parameters that were requested in the Model Constraint command. In our example, these are called a1b1, the indirect effect and total, the total effect.
The seven free parameters, or the seven values that were estimated in our model are the following:
1. the coefficient from detail to opinion;
2. the coefficient from detail to exper;
3. the coefficient from exper to opinion;
4. the intercept for the regression with exper as the outcome;
5. the intercept for the regression with opinion as the outcome;
6. the residual variance for exper; and
7. the residual variance for opinion.
Let’s interpret the coefficients. We will start with the direct effect of Y on X, or opinion on detail. The value of 1.011 is the expected change in opinion (Y) for a one-unit change in detail (X), holding exper (M) constant. Said another way, imagine that you have two cases in your data that have the same value on exper (M), but differ on X by 1 (so one case has a value of X and the other case has a value of X-1). If you subtract the value of Y for the case with a value of X – 1 from the case with a value of X, that difference is estimated to be 1.011. This means that a positive direct effect means that the case higher on detail (X) is estimated to be higher on opinion (Y); a negative direct effect means that the case higher on detail (X) is estimated to be lower on opinion (Y). The other coefficients are interpreted in the same way. The effect of exper (M) on opinion (Y), 0.314, is the expected change in opinion (Y) for a one-unit change in exper, holding detail (X) constant; this is called the “b” path. The effect of exper (M) on detail (X), 0.614, is the expected change in exper, for a one-unit change in detail (X); this is called the “a” path.
Let’s confirm the calculations of the indirect and total effects. The indirect effect is the coefficient of the a path multiplied by the coefficient of the b path: 0.614*0.314 = 0.192796 (which is what we see in the output with some rounding). The total effect is the sum of direct effect and the indirect effect: 1.011 + 0.192796 = 1.204 (again with some rounding).
Below is the diagram produced by Mplus. Please note that diagrams are available only on Windows installations of Mplus.
Notice that there are estimates of the residuals for both outcome variables, exper and opinion, but not for the independent variable, detail. This is an indication of the assumption that the independent variable is measured without error.
Now we will run the same model using the Model Indirect command.
title: simple mediation model - all continuous variables with indirect
! predictor variable - x: detail
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable:
names are detail exper impact opinion ccovar bcovar;
usevariables = detail exper opinion;
analysis:
type = general;
estimator = ml;
model:
opinion on exper;
opinion on detail;
exper on detail;
model: opinion on detail exper;
exper on detail;
model indirect:
opinion ind detail;
Mplus VERSION 8.10
MUTHEN & MUTHEN
INPUT INSTRUCTIONS
title: simple mediation model - all continuous variables with indirect
! predictor variable - x: detail
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable:
names are detail exper impact opinion ccovar bcovar;
usevariables = detail exper opinion;
analysis:
type = general;
estimator = ml;
model:
opinion on exper;
opinion on detail;
exper on detail;
model: opinion on detail exper;
exper on detail;
model indirect:
opinion ind detail;
INPUT READING TERMINATED NORMALLY
simple mediation model - all continuous variables with indirect
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 5000
Number of dependent variables 2
Number of independent variables 1
Number of continuous latent variables 0
Observed dependent variables
Continuous
EXPER OPINION
Observed independent variables
DETAIL
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 1000
Convergence criterion 0.500D-04
Maximum number of steepest descent iterations 20
Input data file(s)
intro_mediation.dat
Input data format FREE
UNIVARIATE SAMPLE STATISTICS
UNIVARIATE HIGHER-ORDER MOMENT DESCRIPTIVE STATISTICS
Variable/ Mean/ Skewness/ Minimum/ % with Percentiles
Sample Size Variance Kurtosis Maximum Min/Max 20%/60% 40%/80% Median
EXPER 131.845 0.034 86.303 0.02% 122.126 128.683 131.802
5000.000 136.500 -0.007 176.176 0.02% 134.746 141.553
OPINION 227.135 0.052 167.442 0.02% 213.095 222.728 227.098
5000.000 268.076 0.010 282.136 0.02% 231.195 240.820
DETAIL 82.884 -0.015 49.943 0.02% 74.894 80.601 82.934
5000.000 89.769 0.041 116.473 0.02% 85.382 90.652
THE MODEL ESTIMATION TERMINATED NORMALLY
MODEL FIT INFORMATION
Number of Free Parameters 7
Loglikelihood
H0 Value -37894.587
H1 Value -37894.587
Information Criteria
Akaike (AIC) 75803.174
Bayesian (BIC) 75848.794
Sample-Size Adjusted BIC 75826.551
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit
Value 0.000
Degrees of Freedom 0
P-Value 0.0000
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.000
90 Percent C.I. 0.000 0.000
Probability RMSEA <= .05 0.000
CFI/TLI
CFI 1.000
TLI 1.000
Chi-Square Test of Model Fit for the Baseline Model
Value 5127.598
Degrees of Freedom 3
P-Value 0.0000
SRMR (Standardized Root Mean Square Residual)
Value 0.000
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
EXPER 0.314 0.016 19.901 0.000
DETAIL 1.011 0.019 51.976 0.000
EXPER ON
DETAIL 0.614 0.015 40.588 0.000
Intercepts
EXPER 80.964 1.262 64.169 0.000
OPINION 101.915 1.901 53.611 0.000
Residual Variances
EXPER 102.672 2.053 50.000 0.000
OPINION 127.810 2.556 50.000 0.000
QUALITY OF NUMERICAL RESULTS
Condition Number for the Information Matrix 0.592E-03
(ratio of smallest to largest eigenvalue)
TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Effects from DETAIL to OPINION
Total 1.204 0.018 68.685 0.000
Total indirect 0.193 0.011 17.868 0.000
Specific indirect 1
OPINION
EXPER
DETAIL 0.193 0.011 17.868 0.000
Direct
OPINION
DETAIL 1.011 0.019 51.976 0.000
DIAGRAM INFORMATION
Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram.
If running Mplus from the Mplus Diagrammer, the diagram opens automatically.
As you can see, the results are identical.
Bootstrapping
While the output above contains all of the values we need, there are some options that would be helpful. Perhaps the most important option changes the method of calculating the standard errors. This is especially important with respect to the indirect effect because it is calculated as the product of two coefficients, and such products are known to be not normally distributed. In Mplus, we add the bootstrap statement to the Analysis command, and we add the Output command with the cint(bcbootstrap) option to get the bias-corrected bootstrapped confidence intervals, which is the preferred type of bootstrapping. A bootstrap option is also available. Note that while the confidence intervals are boostrapped, the standard errors are calculated using the delta method.
In our examples, we use 10,000 bootstrapped replications; for most purposes, that is sufficient. However, while you are still developing and testing your Mplus syntax, you should use a much smaller number, such as 50. Although it does not take much time to run the 10,000 bootstrap replications, running only 50 replications is faster.
Notice that in the previous output, we did not get confidence intervals. If normal-theory confidence intervals are desired, the cinterval statement can be used with no options in the Output command.
title: simple mediation model - all continuous variables with bootstrap
! predictor variable - x: detail
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable: names are detail exper impact opinion ccovar bcovar;
usevariables = detail exper opinion;
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on exper (b1);
opinion on detail (cdash);
exper on detail (a1);
model constraint:
new(a1b1 total);
a1b1 = a1*b1;
total = a1*b1 + cdash;
output:
cint(bcbootstrap);
Mplus VERSION 8.10
MUTHEN & MUTHEN
INPUT INSTRUCTIONS
title: simple mediation model - all continuous variables with bootstrap
! predictor variable - x: detail
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable: names are detail exper impact opinion ccovar bcovar;
usevariables = detail exper opinion;
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on exper (b1);
opinion on detail (cdash);
exper on detail (a1);
model constraint:
new(a1b1 total);
a1b1 = a1*b1;
total = a1*b1 + cdash;
output:
cint(bcbootstrap);
INPUT READING TERMINATED NORMALLY
simple mediation model - all continuous variables with bootstrap
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 5000
Number of dependent variables 2
Number of independent variables 1
Number of continuous latent variables 0
Observed dependent variables
Continuous
EXPER OPINION
Observed independent variables
DETAIL
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 1000
Convergence criterion 0.500D-04
Maximum number of steepest descent iterations 20
Number of bootstrap draws
Requested 10000
Completed 10000
Input data file(s)
intro_mediation.dat
Input data format FREE
UNIVARIATE SAMPLE STATISTICS
UNIVARIATE HIGHER-ORDER MOMENT DESCRIPTIVE STATISTICS
Variable/ Mean/ Skewness/ Minimum/ % with Percentiles
Sample Size Variance Kurtosis Maximum Min/Max 20%/60% 40%/80% Median
EXPER 131.845 0.034 86.303 0.02% 122.126 128.683 131.802
5000.000 136.500 -0.007 176.176 0.02% 134.746 141.553
OPINION 227.135 0.052 167.442 0.02% 213.095 222.728 227.098
5000.000 268.076 0.010 282.136 0.02% 231.195 240.820
DETAIL 82.884 -0.015 49.943 0.02% 74.894 80.601 82.934
5000.000 89.769 0.041 116.473 0.02% 85.382 90.652
THE MODEL ESTIMATION TERMINATED NORMALLY
MODEL FIT INFORMATION
Number of Free Parameters 7
Loglikelihood
H0 Value -37894.587
H1 Value -37894.587
Information Criteria
Akaike (AIC) 75803.174
Bayesian (BIC) 75848.794
Sample-Size Adjusted BIC 75826.551
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit
Value 0.000
Degrees of Freedom 0
P-Value 0.0000
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.000
90 Percent C.I. 0.000 0.000
Probability RMSEA <= .05 0.000
CFI/TLI
CFI 1.000
TLI 1.000
Chi-Square Test of Model Fit for the Baseline Model
Value 5127.598
Degrees of Freedom 3
P-Value 0.0000
SRMR (Standardized Root Mean Square Residual)
Value 0.000
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
EXPER 0.314 0.016 19.845 0.000
DETAIL 1.011 0.019 52.117 0.000
EXPER ON
DETAIL 0.614 0.015 41.116 0.000
Intercepts
EXPER 80.964 1.239 65.321 0.000
OPINION 101.915 1.861 54.763 0.000
Residual Variances
EXPER 102.672 2.086 49.217 0.000
OPINION 127.810 2.597 49.212 0.000
New/Additional Parameters
A1B1 0.193 0.011 17.945 0.000
TOTAL 1.204 0.017 69.235 0.000
CONFIDENCE INTERVALS OF MODEL RESULTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
OPINION ON
EXPER 0.275 0.284 0.289 0.314 0.341 0.346 0.357
DETAIL 0.961 0.973 0.979 1.011 1.043 1.049 1.063
EXPER ON
DETAIL 0.576 0.584 0.589 0.614 0.638 0.643 0.652
Intercepts
EXPER 77.783 78.585 78.939 80.964 82.996 83.385 84.221
OPINION 97.097 98.267 98.849 101.915 105.024 105.548 106.654
Residual Variances
EXPER 97.459 98.714 99.329 102.672 106.225 106.876 107.955
OPINION 121.282 122.806 123.646 127.810 132.239 133.128 134.621
New/Additional Parameters
A1B1 0.166 0.173 0.176 0.193 0.211 0.214 0.222
TOTAL 1.159 1.170 1.175 1.204 1.233 1.239 1.249
DIAGRAM INFORMATION
Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram.
If running Mplus from the Mplus Diagrammer, the diagram opens automatically.
Different types of standardized results
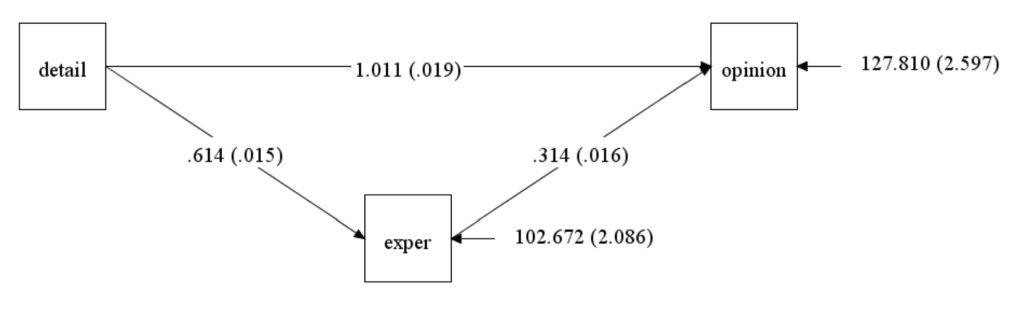
Should the results be presented in the original metric of the variables used in the model, or should the coefficients be standardized? The answer is it depends: do you want to express the results in the original metrics of the variables, or do you want to express the results in terms of standard deviations? If the original metrics of the variables are meaningful, then there may be no need to standardize the results. If the metrics of the variables are arbitrary, then perhaps standardizing is a good idea. The results can be standardized without standardizing the variable before running the model, just as coefficients from a linear regression can be standardized without first standardizing the variables. In Mplus you have three options: stdy, stdyx and standardize. The stdy option standardizes only the Y variable and is interpreted as the change Y standard deviation units when X changes by one unit. Notice that in a mediation model, both the (ultimate) outcome and the mediator are outcome variables, and so they are both standardized. The stdy option may be useful when the independent variable is dichotomous. The stdyx standardizes with respect to both X and Y and is interpreted as the change in Y standard deviation units for a one standard deviation unit change in X. Hayes is careful to note that fully standardized results make sense only when all of the variables in the model are continuous. He warns against standardizing the coefficients of binary predictors, as this may not make much sense substantively. The standardized option includes all possible standardization methods for that model in the output, and thus the output is very long. In the output, the section labeled “STD” is standardized to the latent variable. Of course, there is no latent variable in this model, so the results are identical to the unstandardized output.
In general, it is best to decide what type of standardization to request (if any) depending on the type of interpretation desired and then use the appropriate option. Also note that in some instances, a result may be statistically significant when in its original metric and not statistically significant when standardized, or vice versa. This can happen because the standardized and unstandardized parameter estimates have different sampling distributions. It is possible that one or both sampling distributions is non-normal, having high skewness and kurtosis. If this is the case, the z test-statistic and the symmetric the confidence interval may not cover 0 due to the non-normality and thus lead to the non-significant result. If one of the two parameter estimates has a non-symmetric sampling distribution, then a non-symmetric confidence interval should be used, and this can be obtained with bootstrapping.
title: adding the standardized option
! predictor variable - x: detail
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable: names are detail exper impact opinion ccovar bcovar;
usevariables = detail exper opinion;
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on detail exper;
exper on detail;
model indirect:
opinion ind detail;
output:
standardized cint(bcbootstrap);
Mplus VERSION 8.10
MUTHEN & MUTHEN
INPUT INSTRUCTIONS
title: adding the standardized option
! predictor variable - x: detail
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable: names are detail exper impact opinion ccovar bcovar;
usevariables = detail exper opinion;
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on detail exper;
exper on detail;
model indirect:
opinion ind detail;
output:
standardized cint(bcbootstrap);
INPUT READING TERMINATED NORMALLY
adding the standardized option
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 5000
Number of dependent variables 2
Number of independent variables 1
Number of continuous latent variables 0
Observed dependent variables
Continuous
EXPER OPINION
Observed independent variables
DETAIL
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 1000
Convergence criterion 0.500D-04
Maximum number of steepest descent iterations 20
Number of bootstrap draws
Requested 10000
Completed 10000
Input data file(s)
intro_mediation.dat
Input data format FREE
UNIVARIATE SAMPLE STATISTICS
UNIVARIATE HIGHER-ORDER MOMENT DESCRIPTIVE STATISTICS
Variable/ Mean/ Skewness/ Minimum/ % with Percentiles
Sample Size Variance Kurtosis Maximum Min/Max 20%/60% 40%/80% Median
EXPER 131.845 0.034 86.303 0.02% 122.126 128.683 131.802
5000.000 136.500 -0.007 176.176 0.02% 134.746 141.553
OPINION 227.135 0.052 167.442 0.02% 213.095 222.728 227.098
5000.000 268.076 0.010 282.136 0.02% 231.195 240.820
DETAIL 82.884 -0.015 49.943 0.02% 74.894 80.601 82.934
5000.000 89.769 0.041 116.473 0.02% 85.382 90.652
THE MODEL ESTIMATION TERMINATED NORMALLY
MODEL FIT INFORMATION
Number of Free Parameters 7
Loglikelihood
H0 Value -37894.587
H1 Value -37894.587
Information Criteria
Akaike (AIC) 75803.174
Bayesian (BIC) 75848.794
Sample-Size Adjusted BIC 75826.551
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit
Value 0.000
Degrees of Freedom 0
P-Value 0.0000
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.000
90 Percent C.I. 0.000 0.000
Probability RMSEA <= .05 0.000
CFI/TLI
CFI 1.000
TLI 1.000
Chi-Square Test of Model Fit for the Baseline Model
Value 5127.598
Degrees of Freedom 3
P-Value 0.0000
SRMR (Standardized Root Mean Square Residual)
Value 0.000
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
DETAIL 1.011 0.019 52.117 0.000
EXPER 0.314 0.016 19.845 0.000
EXPER ON
DETAIL 0.614 0.015 41.116 0.000
Intercepts
EXPER 80.964 1.239 65.321 0.000
OPINION 101.915 1.861 54.763 0.000
Residual Variances
EXPER 102.672 2.086 49.217 0.000
OPINION 127.810 2.597 49.212 0.000
STANDARDIZED MODEL RESULTS
STDYX Standardization
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
DETAIL 0.585 0.010 59.054 0.000
EXPER 0.224 0.011 20.001 0.000
EXPER ON
DETAIL 0.498 0.010 47.607 0.000
Intercepts
EXPER 6.930 0.159 43.476 0.000
OPINION 6.225 0.160 38.964 0.000
Residual Variances
EXPER 0.752 0.010 72.284 0.000
OPINION 0.477 0.010 48.968 0.000
STDY Standardization
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
DETAIL 0.062 0.001 59.238 0.000
EXPER 0.224 0.011 20.001 0.000
EXPER ON
DETAIL 0.053 0.001 50.700 0.000
Intercepts
EXPER 6.930 0.159 43.476 0.000
OPINION 6.225 0.160 38.964 0.000
Residual Variances
EXPER 0.752 0.010 72.284 0.000
OPINION 0.477 0.010 48.968 0.000
STD Standardization
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
DETAIL 1.011 0.019 52.117 0.000
EXPER 0.314 0.016 19.845 0.000
EXPER ON
DETAIL 0.614 0.015 41.116 0.000
Intercepts
EXPER 80.964 1.239 65.321 0.000
OPINION 101.915 1.861 54.763 0.000
Residual Variances
EXPER 102.672 2.086 49.217 0.000
OPINION 127.810 2.597 49.212 0.000
R-SQUARE
Observed Two-Tailed
Variable Estimate S.E. Est./S.E. P-Value
EXPER 0.248 0.010 23.816 0.000
OPINION 0.523 0.010 53.741 0.000
TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Effects from DETAIL to OPINION
Total 1.204 0.017 69.235 0.000
Total indirect 0.193 0.011 17.945 0.000
Specific indirect 1
OPINION
EXPER
DETAIL 0.193 0.011 17.945 0.000
Direct
OPINION
DETAIL 1.011 0.019 52.117 0.000
STANDARDIZED TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
STDYX Standardization
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Effects from DETAIL to OPINION
Total 0.697 0.007 94.976 0.000
Total indirect 0.112 0.006 18.500 0.000
Specific indirect 1
OPINION
EXPER
DETAIL 0.112 0.006 18.500 0.000
Direct
OPINION
DETAIL 0.585 0.010 59.054 0.000
STDY Standardization
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Effects from DETAIL to OPINION
Total 0.074 0.001 95.803 0.000
Total indirect 0.012 0.001 18.511 0.000
Specific indirect 1
OPINION
EXPER
DETAIL 0.012 0.001 18.511 0.000
Direct
OPINION
DETAIL 0.062 0.001 59.238 0.000
STD Standardization
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Effects from DETAIL to OPINION
Total 1.204 0.017 69.235 0.000
Total indirect 0.193 0.011 17.945 0.000
Specific indirect 1
OPINION
EXPER
DETAIL 0.193 0.011 17.945 0.000
Direct
OPINION
DETAIL 1.011 0.019 52.117 0.000
CONFIDENCE INTERVALS OF MODEL RESULTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
OPINION ON
DETAIL 0.961 0.973 0.979 1.011 1.043 1.049 1.063
EXPER 0.275 0.284 0.289 0.314 0.341 0.346 0.357
EXPER ON
DETAIL 0.576 0.584 0.589 0.614 0.638 0.643 0.652
Intercepts
EXPER 77.783 78.585 78.939 80.964 82.996 83.385 84.221
OPINION 97.097 98.267 98.849 101.915 105.024 105.548 106.654
Residual Variances
EXPER 97.459 98.714 99.329 102.672 106.225 106.876 107.955
OPINION 121.282 122.806 123.646 127.810 132.239 133.128 134.621
CONFIDENCE INTERVALS OF STANDARDIZED MODEL RESULTS
STDYX Standardization
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
OPINION ON
DETAIL 0.559 0.565 0.569 0.585 0.601 0.604 0.610
EXPER 0.196 0.202 0.206 0.224 0.242 0.246 0.254
EXPER ON
DETAIL 0.470 0.477 0.480 0.498 0.515 0.518 0.523
Intercepts
EXPER 6.517 6.628 6.675 6.930 7.197 7.246 7.342
OPINION 5.823 5.910 5.964 6.225 6.489 6.542 6.641
Residual Variances
EXPER 0.726 0.732 0.735 0.752 0.769 0.773 0.779
OPINION 0.453 0.459 0.461 0.477 0.493 0.497 0.503
STDY Standardization
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
OPINION ON
DETAIL 0.059 0.060 0.060 0.062 0.063 0.064 0.064
EXPER 0.196 0.202 0.206 0.224 0.242 0.246 0.254
EXPER ON
DETAIL 0.050 0.050 0.051 0.053 0.054 0.055 0.055
Intercepts
EXPER 6.517 6.628 6.675 6.930 7.197 7.246 7.342
OPINION 5.823 5.910 5.964 6.225 6.489 6.542 6.641
Residual Variances
EXPER 0.726 0.732 0.735 0.752 0.769 0.773 0.779
OPINION 0.453 0.459 0.461 0.477 0.493 0.497 0.503
STD Standardization
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
OPINION ON
DETAIL 0.961 0.973 0.979 1.011 1.043 1.049 1.063
EXPER 0.275 0.284 0.289 0.314 0.341 0.346 0.357
EXPER ON
DETAIL 0.576 0.584 0.589 0.614 0.638 0.643 0.652
Intercepts
EXPER 77.783 78.585 78.939 80.964 82.996 83.385 84.221
OPINION 97.097 98.267 98.849 101.915 105.024 105.548 106.654
Residual Variances
EXPER 97.459 98.714 99.329 102.672 106.225 106.876 107.955
OPINION 121.282 122.806 123.646 127.810 132.239 133.128 134.621
CONFIDENCE INTERVALS OF TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
Effects from DETAIL to OPINION
Total 1.159 1.170 1.175 1.204 1.233 1.239 1.249
Total indirect 0.166 0.173 0.176 0.193 0.211 0.214 0.222
Specific indirect 1
OPINION
EXPER
DETAIL 0.166 0.173 0.176 0.193 0.211 0.214 0.222
Direct
OPINION
DETAIL 0.961 0.973 0.979 1.011 1.043 1.049 1.063
CONFIDENCE INTERVALS OF STANDARDIZED TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
STDYX Standardization
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
Effects from DETAIL to OPINION
Total 0.677 0.682 0.684 0.697 0.708 0.710 0.715
Total indirect 0.097 0.100 0.102 0.112 0.122 0.124 0.128
Specific indirect 1
OPINION
EXPER
DETAIL 0.097 0.100 0.102 0.112 0.122 0.124 0.128
Direct
OPINION
DETAIL 0.559 0.565 0.569 0.585 0.601 0.604 0.610
STDY Standardization
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
Effects from DETAIL to OPINION
Total 0.072 0.072 0.072 0.074 0.075 0.075 0.075
Total indirect 0.010 0.011 0.011 0.012 0.013 0.013 0.013
Specific indirect 1
OPINION
EXPER
DETAIL 0.010 0.011 0.011 0.012 0.013 0.013 0.013
Direct
OPINION
DETAIL 0.059 0.060 0.060 0.062 0.063 0.064 0.064
STD Standardization
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
Effects from DETAIL to OPINION
Total 1.159 1.170 1.175 1.204 1.233 1.239 1.249
Total indirect 0.166 0.173 0.176 0.193 0.211 0.214 0.222
Specific indirect 1
OPINION
EXPER
DETAIL 0.166 0.173 0.176 0.193 0.211 0.214 0.222
Direct
OPINION
DETAIL 0.961 0.973 0.979 1.011 1.043 1.049 1.063
DIAGRAM INFORMATION
Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram.
If running Mplus from the Mplus Diagrammer, the diagram opens automatically.
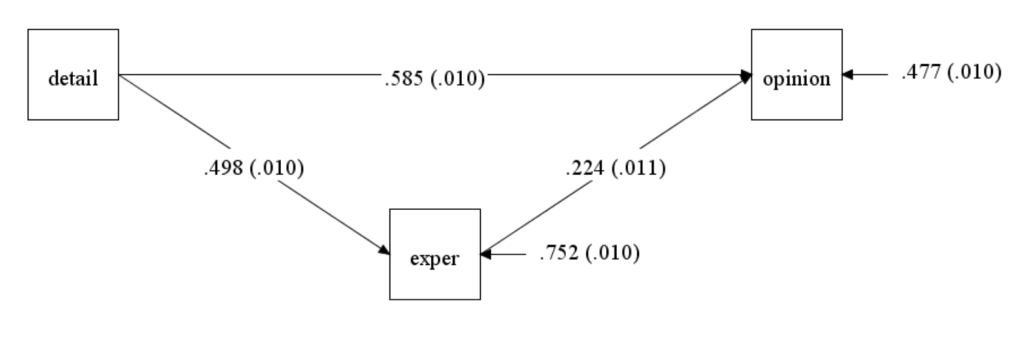
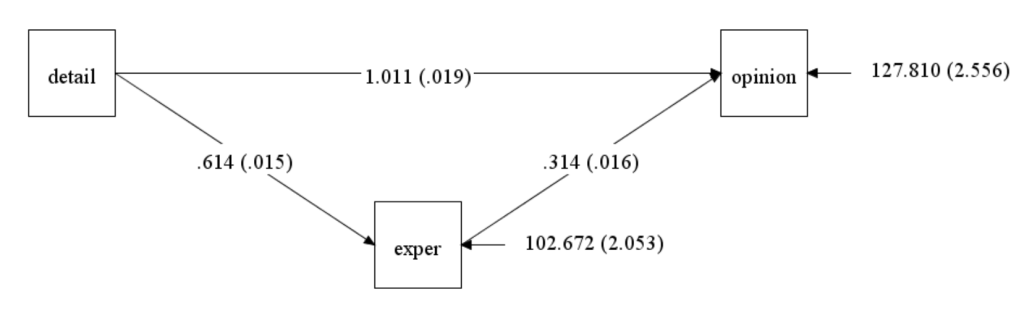
In Mplus, if you click on Diagram and then View Diagram, you will see the diagram of your model with unstandardized coefficients. If you want the standardized coefficients, you can click on View and change the coefficients to your preferred standardization. The stdyx coefficients are shown on the diagram above. You can also change the number of decimal places shown on the diagram by clicking on View and then Specifying Decimal Places.
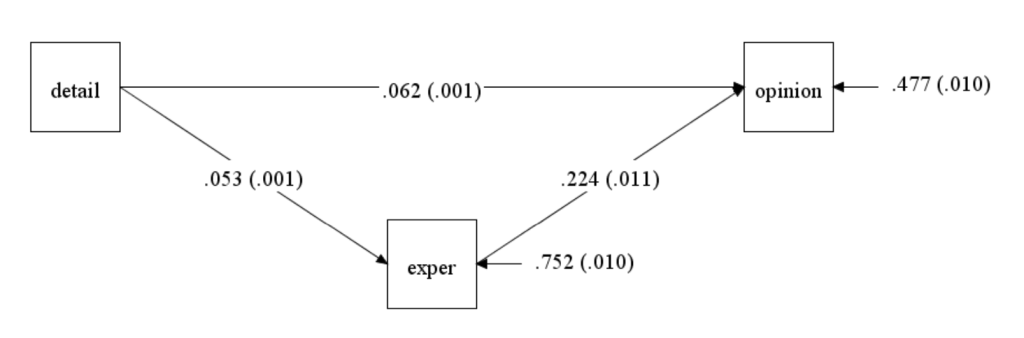
Using the stand option provides a lot of output, some of which we may not need or want. Let’s use just the stdy option and see what output is given.
title: Using just the stdy option
! predictor variable - x: detail
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable: names are detail exper impact opinion ccovar bcovar;
usevariables = detail exper opinion;
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on exper;
opinion on detail;
exper on detail;
model indirect:
opinion ind detail;
output:
stdy cint(bcbootstrap);
Mplus VERSION 8.10
MUTHEN & MUTHEN
INPUT INSTRUCTIONS
title: Using just the stdy option
! predictor variable - x: detail
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable: names are detail exper impact opinion ccovar bcovar;
usevariables = detail exper opinion;
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on exper;
opinion on detail;
exper on detail;
model indirect:
opinion ind detail;
output:
stdy cint(bcbootstrap);
INPUT READING TERMINATED NORMALLY
Using just the stdy option
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 5000
Number of dependent variables 2
Number of independent variables 1
Number of continuous latent variables 0
Observed dependent variables
Continuous
EXPER OPINION
Observed independent variables
DETAIL
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 1000
Convergence criterion 0.500D-04
Maximum number of steepest descent iterations 20
Number of bootstrap draws
Requested 10000
Completed 10000
Input data file(s)
intro_mediation.dat
Input data format FREE
UNIVARIATE SAMPLE STATISTICS
UNIVARIATE HIGHER-ORDER MOMENT DESCRIPTIVE STATISTICS
Variable/ Mean/ Skewness/ Minimum/ % with Percentiles
Sample Size Variance Kurtosis Maximum Min/Max 20%/60% 40%/80% Median
EXPER 131.845 0.034 86.303 0.02% 122.126 128.683 131.802
5000.000 136.500 -0.007 176.176 0.02% 134.746 141.553
OPINION 227.135 0.052 167.442 0.02% 213.095 222.728 227.098
5000.000 268.076 0.010 282.136 0.02% 231.195 240.820
DETAIL 82.884 -0.015 49.943 0.02% 74.894 80.601 82.934
5000.000 89.769 0.041 116.473 0.02% 85.382 90.652
THE MODEL ESTIMATION TERMINATED NORMALLY
MODEL FIT INFORMATION
Number of Free Parameters 7
Loglikelihood
H0 Value -37894.587
H1 Value -37894.587
Information Criteria
Akaike (AIC) 75803.174
Bayesian (BIC) 75848.794
Sample-Size Adjusted BIC 75826.551
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit
Value 0.000
Degrees of Freedom 0
P-Value 0.0000
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.000
90 Percent C.I. 0.000 0.000
Probability RMSEA <= .05 0.000
CFI/TLI
CFI 1.000
TLI 1.000
Chi-Square Test of Model Fit for the Baseline Model
Value 5127.598
Degrees of Freedom 3
P-Value 0.0000
SRMR (Standardized Root Mean Square Residual)
Value 0.000
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
EXPER 0.314 0.016 19.845 0.000
DETAIL 1.011 0.019 52.117 0.000
EXPER ON
DETAIL 0.614 0.015 41.116 0.000
Intercepts
EXPER 80.964 1.239 65.321 0.000
OPINION 101.915 1.861 54.763 0.000
Residual Variances
EXPER 102.672 2.086 49.217 0.000
OPINION 127.810 2.597 49.212 0.000
STANDARDIZED MODEL RESULTS
STDY Standardization
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
EXPER 0.224 0.011 20.001 0.000
DETAIL 0.062 0.001 59.238 0.000
EXPER ON
DETAIL 0.053 0.001 50.700 0.000
Intercepts
EXPER 6.930 0.159 43.476 0.000
OPINION 6.225 0.160 38.964 0.000
Residual Variances
EXPER 0.752 0.010 72.284 0.000
OPINION 0.477 0.010 48.968 0.000
R-SQUARE
Observed Two-Tailed
Variable Estimate S.E. Est./S.E. P-Value
EXPER 0.248 0.010 23.816 0.000
OPINION 0.523 0.010 53.741 0.000
TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Effects from DETAIL to OPINION
Total 1.204 0.017 69.235 0.000
Total indirect 0.193 0.011 17.945 0.000
Specific indirect 1
OPINION
EXPER
DETAIL 0.193 0.011 17.945 0.000
Direct
OPINION
DETAIL 1.011 0.019 52.117 0.000
STANDARDIZED TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
STDY Standardization
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Effects from DETAIL to OPINION
Total 0.074 0.001 95.803 0.000
Total indirect 0.012 0.001 18.511 0.000
Specific indirect 1
OPINION
EXPER
DETAIL 0.012 0.001 18.511 0.000
Direct
OPINION
DETAIL 0.062 0.001 59.238 0.000
CONFIDENCE INTERVALS OF MODEL RESULTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
OPINION ON
EXPER 0.275 0.284 0.289 0.314 0.341 0.346 0.357
DETAIL 0.961 0.973 0.979 1.011 1.043 1.049 1.063
EXPER ON
DETAIL 0.576 0.584 0.589 0.614 0.638 0.643 0.652
Intercepts
EXPER 77.783 78.585 78.939 80.964 82.996 83.385 84.221
OPINION 97.097 98.267 98.849 101.915 105.024 105.548 106.654
Residual Variances
EXPER 97.459 98.714 99.329 102.672 106.225 106.876 107.955
OPINION 121.282 122.806 123.646 127.810 132.239 133.128 134.621
CONFIDENCE INTERVALS OF STANDARDIZED MODEL RESULTS
STDY Standardization
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
OPINION ON
EXPER 0.196 0.202 0.206 0.224 0.242 0.246 0.254
DETAIL 0.059 0.060 0.060 0.062 0.063 0.064 0.064
EXPER ON
DETAIL 0.050 0.050 0.051 0.053 0.054 0.055 0.055
Intercepts
EXPER 6.517 6.628 6.675 6.930 7.197 7.246 7.342
OPINION 5.823 5.910 5.964 6.225 6.489 6.542 6.641
Residual Variances
EXPER 0.726 0.732 0.735 0.752 0.769 0.773 0.779
OPINION 0.453 0.459 0.461 0.477 0.493 0.497 0.503
CONFIDENCE INTERVALS OF TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
Effects from DETAIL to OPINION
Total 1.159 1.170 1.175 1.204 1.233 1.239 1.249
Total indirect 0.166 0.173 0.176 0.193 0.211 0.214 0.222
Specific indirect 1
OPINION
EXPER
DETAIL 0.166 0.173 0.176 0.193 0.211 0.214 0.222
Direct
OPINION
DETAIL 0.961 0.973 0.979 1.011 1.043 1.049 1.063
CONFIDENCE INTERVALS OF STANDARDIZED TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
STDY Standardization
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
Effects from DETAIL to OPINION
Total 0.072 0.072 0.072 0.074 0.075 0.075 0.075
Total indirect 0.010 0.011 0.011 0.012 0.013 0.013 0.013
Specific indirect 1
OPINION
EXPER
DETAIL 0.010 0.011 0.011 0.012 0.013 0.013 0.013
Direct
OPINION
DETAIL 0.059 0.060 0.060 0.062 0.063 0.064 0.064
DIAGRAM INFORMATION
Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram.
If running Mplus from the Mplus Diagrammer, the diagram opens automatically.
Simple mediation model with binary predictor
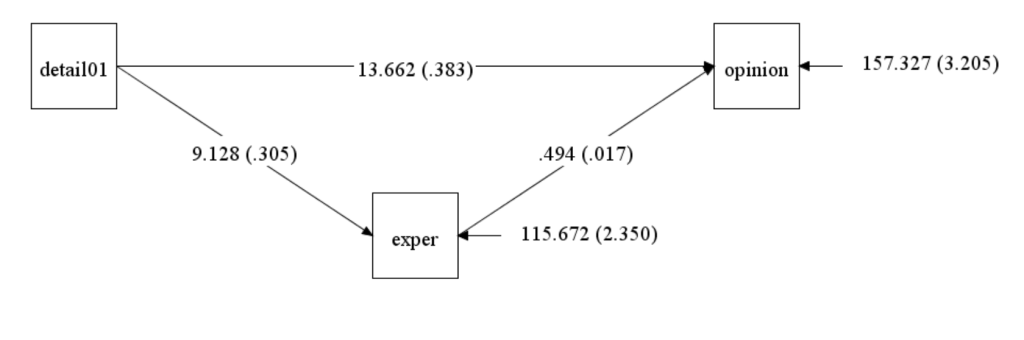
Let’s modify this example just a little by using a binary predictor (X) instead of a continuous predictor. We do not have a binary variable in our dataset to use as the example, so we will create one. In general, we do not recommend creating a binary predictor from a continuous predictor because information is lost. However, it is good to know how to create variables in Mplus. There are at least two ways to create a binary variable. In this example, we show the use of the Define command and create the new binary variable we call detail01. (The syntax to do this looks very much like SAS syntax.) As you might expect, interpretation will be the same as when the predictor variable detail was continuous. As stated on page 85 of Hayes’ book, “In the special case where X is dichotomous, with the two values of X differing by a single unit (e.g., X = 1 and X = 0), Ŷ can be interpreted as a group mean, …, meaning c’ estimates the difference between the two group means holding M constant. This is equivalent to what in analysis of covariance terms is called an adjusted mean difference.”
title: simple mediation with binary predictor with if statement
! binary predictor variable - x: detail01
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable:
names are detail exper impact opinion ccovar bcovar;
usevariables = exper opinion detail01;
define:
detail01 = 0;
if detail gt 83 then detail01 = 1;
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on detail01 exper;
exper on detail01;
model indirect:
opinion ind detail01;
output:
cint(bcbootstrap);
Mplus VERSION 8.10
MUTHEN & MUTHEN
INPUT INSTRUCTIONS
title: simple mediation with binary predictor with if statement
! binary predictor variable - x: detail01
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable:
names are detail exper impact opinion ccovar bcovar;
usevariables = exper opinion detail01;
define:
detail01 = 0;
if detail gt 83 then detail01 = 1;
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on detail01 exper;
exper on detail01;
model indirect:
opinion ind detail01;
output:
cint(bcbootstrap);
INPUT READING TERMINATED NORMALLY
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 5000
Number of dependent variables 2
Number of independent variables 1
Number of continuous latent variables 0
Observed dependent variables
Continuous
EXPER OPINION
Observed independent variables
DETAIL01
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 1000
Convergence criterion 0.500D-04
Maximum number of steepest descent iterations 20
Number of bootstrap draws
Requested 10000
Completed 10000
Input data file(s)
intro_mediation.dat
Input data format FREE
UNIVARIATE SAMPLE STATISTICS
UNIVARIATE HIGHER-ORDER MOMENT DESCRIPTIVE STATISTICS
Variable/ Mean/ Skewness/ Minimum/ % with Percentiles
Sample Size Variance Kurtosis Maximum Min/Max 20%/60% 40%/80% Median
EXPER 131.845 0.034 86.303 0.02% 122.126 128.683 131.802
5000.000 136.500 -0.007 176.176 0.02% 134.746 141.553
OPINION 227.135 0.052 167.442 0.02% 213.095 222.728 227.098
5000.000 268.076 0.010 282.136 0.02% 231.195 240.820
DETAIL01 0.495 0.018 0.000 50.46% 0.000 0.000 0.000
5000.000 0.250 -2.000 1.000 49.54% 1.000 1.000
THE MODEL ESTIMATION TERMINATED NORMALLY
MODEL FIT INFORMATION
Number of Free Parameters 7
Loglikelihood
H0 Value -38712.109
H1 Value -38712.109
Information Criteria
Akaike (AIC) 77438.217
Bayesian (BIC) 77483.837
Sample-Size Adjusted BIC 77461.594
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit
Value 0.000
Degrees of Freedom 0
P-Value 0.0000
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.000
90 Percent C.I. 0.000 0.000
Probability RMSEA <= .05 0.000
CFI/TLI
CFI 1.000
TLI 1.000
Chi-Square Test of Model Fit for the Baseline Model
Value 3492.554
Degrees of Freedom 3
P-Value 0.0000
SRMR (Standardized Root Mean Square Residual)
Value 0.000
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
DETAIL01 13.662 0.383 35.692 0.000
EXPER 0.494 0.017 29.416 0.000
EXPER ON
DETAIL01 9.128 0.305 29.918 0.000
Intercepts
EXPER 127.323 0.210 606.612 0.000
OPINION 155.249 2.156 72.016 0.000
Residual Variances
EXPER 115.672 2.350 49.224 0.000
OPINION 157.327 3.205 49.094 0.000
TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Effects from DETAIL01 to OPINION
Total 18.170 0.389 46.732 0.000
Total indirect 4.508 0.215 20.925 0.000
Specific indirect 1
OPINION
EXPER
DETAIL01 4.508 0.215 20.925 0.000
Direct
OPINION
DETAIL01 13.662 0.383 35.692 0.000
CONFIDENCE INTERVALS OF MODEL RESULTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
OPINION ON
DETAIL01 12.698 12.913 13.037 13.662 14.292 14.417 14.670
EXPER 0.451 0.461 0.466 0.494 0.521 0.527 0.537
EXPER ON
DETAIL01 8.340 8.526 8.625 9.128 9.627 9.730 9.923
Intercepts
EXPER 126.780 126.924 126.984 127.323 127.675 127.743 127.868
OPINION 149.648 151.006 151.738 155.249 158.790 159.454 160.721
Residual Variances
EXPER 109.790 111.238 111.902 115.672 119.599 120.342 122.018
OPINION 149.107 151.029 152.043 157.327 162.600 163.576 165.331
CONFIDENCE INTERVALS OF TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
Effects from DETAIL01 to OPINION
Total 17.164 17.419 17.527 18.170 18.813 18.930 19.174
Total indirect 3.963 4.101 4.171 4.508 4.880 4.946 5.075
Specific indirect 1
OPINION
EXPER
DETAIL01 3.963 4.101 4.171 4.508 4.880 4.946 5.075
Direct
OPINION
DETAIL01 12.698 12.913 13.037 13.662 14.292 14.417 14.670
DIAGRAM INFORMATION
Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram.
If running Mplus from the Mplus Diagrammer, the diagram opens automatically.
We can also use the cut statement in the Define command.
title: simple mediation with binary predictor with cut
! binary predictor variable - x: detail01
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable:
names are detail exper impact opinion ccovar bcovar;
usevariables = exper opinion detail;
define:
cut detail (83);
analysis: type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on exper;
opinion on detail;
exper on detail;
model indirect:
opinion ind detail;
output:
cint(bcbootstrap);
Mplus VERSION 8.10
MUTHEN & MUTHEN
INPUT INSTRUCTIONS
title: simple mediation with binary predictor with cut
! binary predictor variable - x: detail01
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable:
names are detail exper impact opinion ccovar bcovar;
usevariables = exper opinion detail;
define:
cut detail (83);
analysis: type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on exper;
opinion on detail;
exper on detail;
model indirect:
opinion ind detail;
output:
cint(bcbootstrap);
INPUT READING TERMINATED NORMALLY
simple mediation with binary predictor with cut
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 5000
Number of dependent variables 2
Number of independent variables 1
Number of continuous latent variables 0
Observed dependent variables
Continuous
EXPER OPINION
Observed independent variables
DETAIL
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 1000
Convergence criterion 0.500D-04
Maximum number of steepest descent iterations 20
Number of bootstrap draws
Requested 10000
Completed 10000
Input data file(s)
intro_mediation.dat
Input data format FREE
UNIVARIATE SAMPLE STATISTICS
UNIVARIATE HIGHER-ORDER MOMENT DESCRIPTIVE STATISTICS
Variable/ Mean/ Skewness/ Minimum/ % with Percentiles
Sample Size Variance Kurtosis Maximum Min/Max 20%/60% 40%/80% Median
EXPER 131.845 0.034 86.303 0.02% 122.126 128.683 131.802
5000.000 136.500 -0.007 176.176 0.02% 134.746 141.553
OPINION 227.135 0.052 167.442 0.02% 213.095 222.728 227.098
5000.000 268.076 0.010 282.136 0.02% 231.195 240.820
DETAIL 0.495 0.018 0.000 50.46% 0.000 0.000 0.000
5000.000 0.250 -2.000 1.000 49.54% 1.000 1.000
THE MODEL ESTIMATION TERMINATED NORMALLY
MODEL FIT INFORMATION
Number of Free Parameters 7
Loglikelihood
H0 Value -38712.109
H1 Value -38712.109
Information Criteria
Akaike (AIC) 77438.217
Bayesian (BIC) 77483.837
Sample-Size Adjusted BIC 77461.594
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit
Value 0.000
Degrees of Freedom 0
P-Value 0.0000
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.000
90 Percent C.I. 0.000 0.000
Probability RMSEA <= .05 0.000
CFI/TLI
CFI 1.000
TLI 1.000
Chi-Square Test of Model Fit for the Baseline Model
Value 3492.554
Degrees of Freedom 3
P-Value 0.0000
SRMR (Standardized Root Mean Square Residual)
Value 0.000
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
EXPER 0.494 0.017 29.416 0.000
DETAIL 13.662 0.383 35.692 0.000
EXPER ON
DETAIL 9.128 0.305 29.918 0.000
Intercepts
EXPER 127.323 0.210 606.612 0.000
OPINION 155.249 2.156 72.016 0.000
Residual Variances
EXPER 115.672 2.350 49.224 0.000
OPINION 157.327 3.205 49.094 0.000
TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Effects from DETAIL to OPINION
Total 18.170 0.389 46.732 0.000
Total indirect 4.508 0.215 20.925 0.000
Specific indirect 1
OPINION
EXPER
DETAIL 4.508 0.215 20.925 0.000
Direct
OPINION
DETAIL 13.662 0.383 35.692 0.000
CONFIDENCE INTERVALS OF MODEL RESULTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
OPINION ON
EXPER 0.451 0.461 0.466 0.494 0.521 0.527 0.537
DETAIL 12.698 12.913 13.037 13.662 14.292 14.417 14.670
EXPER ON
DETAIL 8.340 8.526 8.625 9.128 9.627 9.730 9.923
Intercepts
EXPER 126.780 126.924 126.984 127.323 127.675 127.743 127.868
OPINION 149.648 151.006 151.738 155.249 158.790 159.454 160.721
Residual Variances
EXPER 109.790 111.238 111.902 115.672 119.599 120.342 122.018
OPINION 149.107 151.029 152.043 157.327 162.600 163.576 165.331
CONFIDENCE INTERVALS OF TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
Effects from DETAIL to OPINION
Total 17.164 17.419 17.527 18.170 18.813 18.930 19.174
Total indirect 3.963 4.101 4.171 4.508 4.880 4.946 5.075
Specific indirect 1
OPINION
EXPER
DETAIL 3.963 4.101 4.171 4.508 4.880 4.946 5.075
Direct
OPINION
DETAIL 12.698 12.913 13.037 13.662 14.292 14.417 14.670
DIAGRAM INFORMATION
Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram.
If running Mplus from the Mplus Diagrammer, the diagram opens automatically.
Let’s get standardized results and see what happens.
title: simple mediation with binary predictor with cut and standardized results
! binary predictor variable - x: detail01
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable:
names are detail exper impact opinion ccovar bcovar;
usevariables = exper opinion detail;
define:
cut detail (83);
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on exper;
opinion on detail;
exper on detail;
model indirect: opinion ind detail;
output:
stdy cint(bcbootstrap);
Mplus VERSION 8.10
MUTHEN & MUTHEN
INPUT INSTRUCTIONS
title: simple mediation with binary predictor with cut and standardized results
! binary predictor variable - x: detail01
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable:
names are detail exper impact opinion ccovar bcovar;
usevariables = exper opinion detail;
define:
cut detail (83);
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on exper;
opinion on detail;
exper on detail;
model indirect: opinion ind detail;
output:
stdy cint(bcbootstrap);
INPUT READING TERMINATED NORMALLY
simple mediation with binary predictor with cut and standardized results
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 5000
Number of dependent variables 2
Number of independent variables 1
Number of continuous latent variables 0
Observed dependent variables
Continuous
EXPER OPINION
Observed independent variables
DETAIL
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 1000
Convergence criterion 0.500D-04
Maximum number of steepest descent iterations 20
Number of bootstrap draws
Requested 10000
Completed 10000
Input data file(s)
intro_mediation.dat
Input data format FREE
UNIVARIATE SAMPLE STATISTICS
UNIVARIATE HIGHER-ORDER MOMENT DESCRIPTIVE STATISTICS
Variable/ Mean/ Skewness/ Minimum/ % with Percentiles
Sample Size Variance Kurtosis Maximum Min/Max 20%/60% 40%/80% Median
EXPER 131.845 0.034 86.303 0.02% 122.126 128.683 131.802
5000.000 136.500 -0.007 176.176 0.02% 134.746 141.553
OPINION 227.135 0.052 167.442 0.02% 213.095 222.728 227.098
5000.000 268.076 0.010 282.136 0.02% 231.195 240.820
DETAIL 0.495 0.018 0.000 50.46% 0.000 0.000 0.000
5000.000 0.250 -2.000 1.000 49.54% 1.000 1.000
THE MODEL ESTIMATION TERMINATED NORMALLY
MODEL FIT INFORMATION
Number of Free Parameters 7
Loglikelihood
H0 Value -38712.109
H1 Value -38712.109
Information Criteria
Akaike (AIC) 77438.217
Bayesian (BIC) 77483.837
Sample-Size Adjusted BIC 77461.594
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit
Value 0.000
Degrees of Freedom 0
P-Value 0.0000
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.000
90 Percent C.I. 0.000 0.000
Probability RMSEA <= .05 0.000
CFI/TLI
CFI 1.000
TLI 1.000
Chi-Square Test of Model Fit for the Baseline Model
Value 3492.554
Degrees of Freedom 3
P-Value 0.0000
SRMR (Standardized Root Mean Square Residual)
Value 0.000
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
EXPER 0.494 0.017 29.416 0.000
DETAIL 13.662 0.383 35.692 0.000
EXPER ON
DETAIL 9.128 0.305 29.918 0.000
Intercepts
EXPER 127.323 0.210 606.612 0.000
OPINION 155.249 2.156 72.016 0.000
Residual Variances
EXPER 115.672 2.350 49.224 0.000
OPINION 157.327 3.205 49.094 0.000
STANDARDIZED MODEL RESULTS
STDY Standardization
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
EXPER 0.352 0.011 30.888 0.000
DETAIL 0.834 0.021 39.422 0.000
EXPER ON
DETAIL 0.781 0.023 34.092 0.000
Intercepts
EXPER 10.898 0.119 91.957 0.000
OPINION 9.482 0.193 49.053 0.000
Residual Variances
EXPER 0.847 0.009 94.738 0.000
OPINION 0.587 0.010 58.026 0.000
R-SQUARE
Observed Two-Tailed
Variable Estimate S.E. Est./S.E. P-Value
EXPER 0.153 0.009 17.058 0.000
OPINION 0.413 0.010 40.847 0.000
TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Effects from DETAIL to OPINION
Total 18.170 0.389 46.732 0.000
Total indirect 4.508 0.215 20.925 0.000
Specific indirect 1
OPINION
EXPER
DETAIL 4.508 0.215 20.925 0.000
Direct
OPINION
DETAIL 13.662 0.383 35.692 0.000
STANDARDIZED TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
STDY Standardization
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Effects from DETAIL to OPINION
Total 1.110 0.018 62.074 0.000
Total indirect 0.275 0.012 22.864 0.000
Specific indirect 1
OPINION
EXPER
DETAIL 0.275 0.012 22.864 0.000
Direct
OPINION
DETAIL 0.834 0.021 39.422 0.000
CONFIDENCE INTERVALS OF MODEL RESULTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
OPINION ON
EXPER 0.451 0.461 0.466 0.494 0.521 0.527 0.537
DETAIL 12.698 12.913 13.037 13.662 14.292 14.417 14.670
EXPER ON
DETAIL 8.340 8.526 8.625 9.128 9.627 9.730 9.923
Intercepts
EXPER 126.780 126.924 126.984 127.323 127.675 127.743 127.868
OPINION 149.648 151.006 151.738 155.249 158.790 159.454 160.721
Residual Variances
EXPER 109.790 111.238 111.902 115.672 119.599 120.342 122.018
OPINION 149.107 151.029 152.043 157.327 162.600 163.576 165.331
CONFIDENCE INTERVALS OF STANDARDIZED MODEL RESULTS
STDY Standardization
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
OPINION ON
EXPER 0.323 0.330 0.334 0.352 0.371 0.375 0.381
DETAIL 0.780 0.792 0.799 0.834 0.869 0.875 0.888
EXPER ON
DETAIL 0.720 0.735 0.742 0.781 0.818 0.826 0.840
Intercepts
EXPER 10.593 10.678 10.712 10.898 11.099 11.137 11.212
OPINION 8.988 9.108 9.171 9.482 9.805 9.865 9.989
Residual Variances
EXPER 0.824 0.830 0.833 0.847 0.862 0.865 0.870
OPINION 0.562 0.568 0.571 0.587 0.604 0.607 0.614
CONFIDENCE INTERVALS OF TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
Effects from DETAIL to OPINION
Total 17.164 17.419 17.527 18.170 18.813 18.930 19.174
Total indirect 3.963 4.101 4.171 4.508 4.880 4.946 5.075
Specific indirect 1
OPINION
EXPER
DETAIL 3.963 4.101 4.171 4.508 4.880 4.946 5.075
Direct
OPINION
DETAIL 12.698 12.913 13.037 13.662 14.292 14.417 14.670
CONFIDENCE INTERVALS OF STANDARDIZED TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
STDY Standardization
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
Effects from DETAIL to OPINION
Total 1.064 1.074 1.079 1.110 1.139 1.144 1.154
Total indirect 0.244 0.252 0.256 0.275 0.296 0.300 0.307
Specific indirect 1
OPINION
EXPER
DETAIL 0.244 0.252 0.256 0.275 0.296 0.300 0.307
Direct
OPINION
DETAIL 0.780 0.792 0.799 0.834 0.869 0.875 0.888
DIAGRAM INFORMATION
Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram.
If running Mplus from the Mplus Diagrammer, the diagram opens automatically.
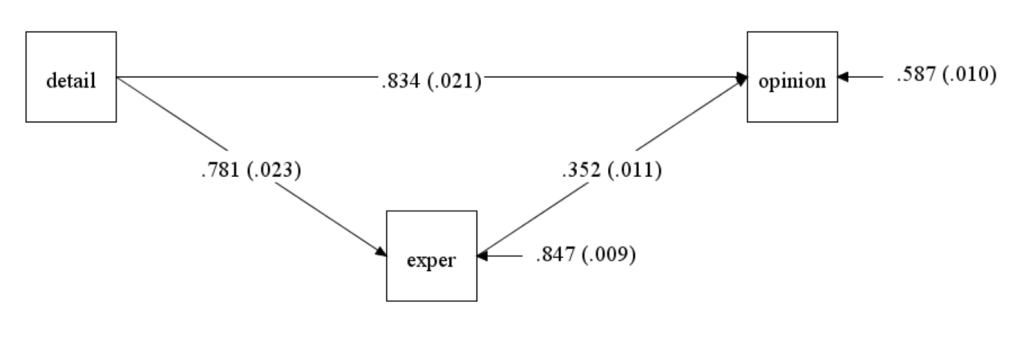We interpret the standardized output as a change in standard deviation units for Y for a one-unit change in X. With respect to our example, we would say that we expect a 0.781 standard deviation change in exper for a one-unit change in detail. We expect a 0.834 standard deviation change in opinion for a one-unit change in detail, holding exper constant. We expect a 0.352 standard deviation change in opinion for a one-unit change in exper, holding detail constant.
Simple mediation model with multicategorical predictor
Now let’s try using a predictor (X) that has three levels. It does not matter if the predictor variable is ordinal (has ordered categories) or if it is nominal (unordered categories), just as it does not matter in regression analysis. What does matter is how you code the categories, just as it does in regression. Because indicator (AKA dummy) coding is so frequently used, we will use it in this example. If you do not have this variable in your dataset, you can make it using statements in the Define command. We will use the lowest-numbered category as our reference group. (Please see Regression for SPSS Chapter 5: Additional coding systems for categorical variables in regression analysis for more information on different types of coding systems.)
We use the Define command to create the dummy variables. The values at which the variable detail is cut were determined by the descriptive information given at the beginning of the previous outputs.
Notice that in the Mplus code below, there is no mention of the relationship between detail2 and detail3. There is, however, a curved double-headed arrow between these two dummy variables in the diagram. No estimate of this correlation/covariance is given in either the output or on the diagram, and that correlation/covariance is not included in the count of free parameters. Hence, while this value is estimated, it is not reported. If that correlation/covariance is specifically set to 0 in the Mplus code, an warning message will be give. Because there should be a relationship between detail2 and detail3, we do not recommend setting this estimate to 0.
title: simple mediation model with three-level predictor
! 3 level predictor variable - x: detail3
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data:
file is intro_mediation.dat;
variable:
names are detail exper impact opinion ccovar bcovar;
usevariables = exper opinion detail2 detail3;
define:
detail2 = 0;
if detail gt 76 then detail2 = 1;
if detail gt 91 then detail2 = 0;
detail3 = 0; if detail gt 91 then detail3 = 1;
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on detail2 detail3 exper;
exper on detail2 detail3;
model indirect:
opinion ind detail2;
opinion ind detail3;
output:
cint(bcbootstrap);
Mplus VERSION 8.10
MUTHEN & MUTHEN
INPUT INSTRUCTIONS
title: simple mediation model with three-level predictor
! 3 level predictor variable - x: detail3
! mediator variable(s) - m: exper
! outcome variable - y: opinion
data:
file is intro_mediation.dat;
variable:
names are detail exper impact opinion ccovar bcovar;
usevariables = exper opinion detail2 detail3;
define:
detail2 = 0;
if detail gt 76 then detail2 = 1;
if detail gt 91 then detail2 = 0;
detail3 = 0; if detail gt 91 then detail3 = 1;
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on detail2 detail3 exper;
exper on detail2 detail3;
model indirect:
opinion ind detail2;
opinion ind detail3;
output:
cint(bcbootstrap);
INPUT READING TERMINATED NORMALLY
simple mediation model with three-level predictor
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 5000
Number of dependent variables 2
Number of independent variables 2
Number of continuous latent variables 0
Observed dependent variables
Continuous
EXPER OPINION
Observed independent variables
DETAIL2 DETAIL3
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 1000
Convergence criterion 0.500D-04
Maximum number of steepest descent iterations 20
Number of bootstrap draws
Requested 10000
Completed 10000
Input data file(s)
intro_mediation.dat
Input data format FREE
UNIVARIATE SAMPLE STATISTICS
UNIVARIATE HIGHER-ORDER MOMENT DESCRIPTIVE STATISTICS
Variable/ Mean/ Skewness/ Minimum/ % with Percentiles
Sample Size Variance Kurtosis Maximum Min/Max 20%/60% 40%/80% Median
EXPER 131.845 0.034 86.303 0.02% 122.126 128.683 131.802
5000.000 136.500 -0.007 176.176 0.02% 134.746 141.553
OPINION 227.135 0.052 167.442 0.02% 213.095 222.728 227.098
5000.000 268.076 0.010 282.136 0.02% 231.195 240.820
DETAIL2 0.579 -0.322 0.000 42.06% 0.000 0.000 1.000
5000.000 0.244 -1.897 1.000 57.94% 1.000 1.000
DETAIL3 0.189 1.590 0.000 81.12% 0.000 0.000 0.000
5000.000 0.153 0.529 1.000 18.88% 0.000 0.000
THE MODEL ESTIMATION TERMINATED NORMALLY
MODEL FIT INFORMATION
Number of Free Parameters 9
Loglikelihood
H0 Value -38401.722
H1 Value -38401.722
Information Criteria
Akaike (AIC) 76821.443
Bayesian (BIC) 76880.098
Sample-Size Adjusted BIC 76851.499
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit
Value 0.000
Degrees of Freedom 0
P-Value 0.0000
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.000
90 Percent C.I. 0.000 0.000
Probability RMSEA <= .05 0.000
CFI/TLI
CFI 1.000
TLI 1.000
Chi-Square Test of Model Fit for the Baseline Model
Value 4113.328
Degrees of Freedom 5
P-Value 0.0000
SRMR (Standardized Root Mean Square Residual)
Value 0.000
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
DETAIL2 11.987 0.423 28.344 0.000
DETAIL3 24.639 0.569 43.339 0.000
EXPER 0.424 0.016 26.519 0.000
EXPER ON
DETAIL2 7.998 0.363 22.021 0.000
DETAIL3 15.777 0.460 34.325 0.000
Intercepts
EXPER 124.231 0.304 408.497 0.000
OPINION 159.579 2.029 78.651 0.000
Residual Variances
EXPER 110.395 2.241 49.269 0.000
OPINION 145.601 2.922 49.823 0.000
TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Effects from DETAIL2 to OPINION
Total 15.382 0.439 35.067 0.000
Total indirect 3.395 0.202 16.806 0.000
Specific indirect 1
OPINION
EXPER
DETAIL2 3.395 0.202 16.806 0.000
Direct
OPINION
DETAIL2 11.987 0.423 28.344 0.000
Effects from DETAIL3 to OPINION
Total 31.335 0.559 56.042 0.000
Total indirect 6.696 0.321 20.869 0.000
Specific indirect 1
OPINION
EXPER
DETAIL3 6.696 0.321 20.869 0.000
Direct
OPINION
DETAIL3 24.639 0.569 43.339 0.000
CONFIDENCE INTERVALS OF MODEL RESULTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
OPINION ON
DETAIL2 10.900 11.154 11.295 11.987 12.679 12.814 13.077
DETAIL3 23.156 23.540 23.703 24.639 25.582 25.757 26.126
EXPER 0.384 0.394 0.399 0.424 0.451 0.456 0.467
EXPER ON
DETAIL2 7.021 7.272 7.386 7.998 8.588 8.699 8.915
DETAIL3 14.585 14.884 15.030 15.777 16.532 16.674 16.963
Intercepts
EXPER 123.453 123.639 123.726 124.231 124.737 124.845 125.010
OPINION 154.188 155.543 156.166 159.579 162.845 163.488 164.745
Residual Variances
EXPER 104.863 106.190 106.814 110.395 114.237 114.928 116.217
OPINION 138.124 140.018 140.856 145.601 150.565 151.456 153.281
CONFIDENCE INTERVALS OF TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
Effects from DETAIL2 to OPINION
Total 14.193 14.503 14.643 15.382 16.088 16.222 16.490
Total indirect 2.888 3.002 3.069 3.395 3.727 3.795 3.937
Specific indirect 1
OPINION
EXPER
DETAIL2 2.888 3.002 3.069 3.395 3.727 3.795 3.937
Direct
OPINION
DETAIL2 10.900 11.154 11.295 11.987 12.679 12.814 13.077
Effects from DETAIL3 to OPINION
Total 29.864 30.229 30.404 31.335 32.254 32.444 32.757
Total indirect 5.910 6.103 6.192 6.696 7.240 7.358 7.577
Specific indirect 1
OPINION
EXPER
DETAIL3 5.910 6.103 6.192 6.696 7.240 7.358 7.577
Direct
OPINION
DETAIL3 23.155 23.540 23.703 24.639 25.582 25.757 26.126
DIAGRAM INFORMATION
Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram.
If running Mplus from the Mplus Diagrammer, the diagram opens automatically.
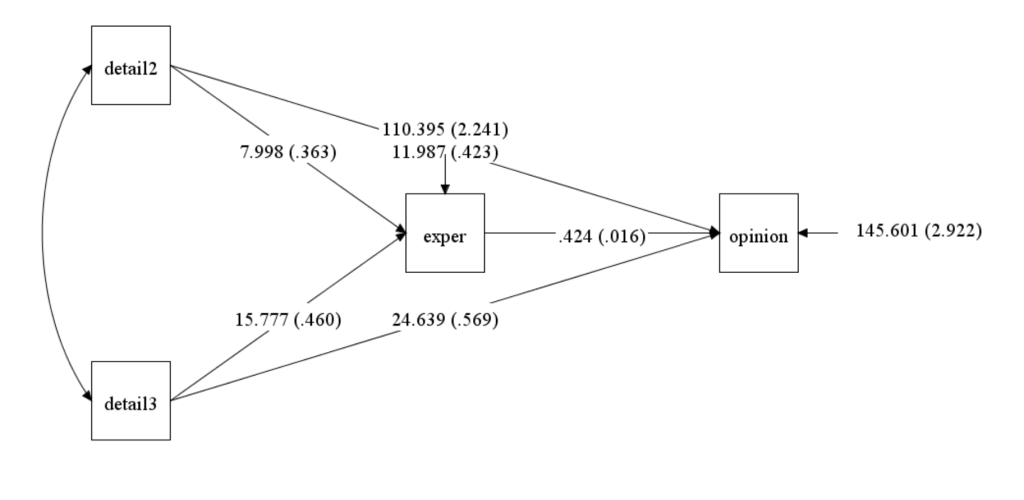To get the omnibus test of the dummy variables that represent the independent variable, the Model Test command can be added. Notice that we must label d2 and d3, and therefore these variables must be listed at the end of the line, making the line wrap a few times before the semi-colon ends the statement. In the Model Test command, we add two lines of code, setting each parameter for each dummy variable to 0.
Note that the Model Test command does not work with bootstrapping, so we run a slightly different program simply to get the omnibus test. The new part of the output is found at the end of the Model Fit Information section and is titled the Wald Test of Parameter Constraints.
title: simple mediation model with three-level predictor
! 3 level predictor variable - x: detail3
! mediator variable(s) - m: exper
! outcome variable - y: opinion
! model test does not work with bootstrap
data:
file is intro_mediation.dat;
variable:
names are detail exper impact opinion ccovar bcovar;
usevariables = exper opinion detail2 detail3;
define: detail2 = 0;
if detail gt 76 then detail2 = 1;
if detail gt 91 then detail2 = 0;
detail3 = 0; if detail gt 91 then detail3 = 1;
analysis:
type = general;
estimator = ml;
model:
opinion on detail2 (d2)
detail3 (d3)
exper;
exper on detail2 detail3;
model indirect:
opinion ind detail2;
opinion ind detail3;
model test:
0 = d2;
0 = d3;
Mplus VERSION 8.10
MUTHEN & MUTHEN
INPUT INSTRUCTIONS
title: simple mediation model with three-level predictor
! 3 level predictor variable - x: detail3
! mediator variable(s) - m: exper
! outcome variable - y: opinion
! model test does not work with bootstrap
data:
file is intro_mediation.dat;
variable:
names are detail exper impact opinion ccovar bcovar;
usevariables = exper opinion detail2 detail3;
define: detail2 = 0;
if detail gt 76 then detail2 = 1;
if detail gt 91 then detail2 = 0;
detail3 = 0; if detail gt 91 then detail3 = 1;
analysis:
type = general;
estimator = ml;
model:
opinion on detail2 (d2)
detail3 (d3)
exper;
exper on detail2 detail3;
model indirect:
opinion ind detail2;
opinion ind detail3;
model test:
0 = d2;
0 = d3;
INPUT READING TERMINATED NORMALLY
simple mediation model with three-level predictor
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 5000
Number of dependent variables 2
Number of independent variables 2
Number of continuous latent variables 0
Observed dependent variables
Continuous
EXPER OPINION
Observed independent variables
DETAIL2 DETAIL3
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 1000
Convergence criterion 0.500D-04
Maximum number of steepest descent iterations 20
Input data file(s)
intro_mediation.dat
Input data format FREE
UNIVARIATE SAMPLE STATISTICS
UNIVARIATE HIGHER-ORDER MOMENT DESCRIPTIVE STATISTICS
Variable/ Mean/ Skewness/ Minimum/ % with Percentiles
Sample Size Variance Kurtosis Maximum Min/Max 20%/60% 40%/80% Median
EXPER 131.845 0.034 86.303 0.02% 122.126 128.683 131.802
5000.000 136.500 -0.007 176.176 0.02% 134.746 141.553
OPINION 227.135 0.052 167.442 0.02% 213.095 222.728 227.098
5000.000 268.076 0.010 282.136 0.02% 231.195 240.820
DETAIL2 0.579 -0.322 0.000 42.06% 0.000 0.000 1.000
5000.000 0.244 -1.897 1.000 57.94% 1.000 1.000
DETAIL3 0.189 1.590 0.000 81.12% 0.000 0.000 0.000
5000.000 0.153 0.529 1.000 18.88% 0.000 0.000
THE MODEL ESTIMATION TERMINATED NORMALLY
MODEL FIT INFORMATION
Number of Free Parameters 9
Loglikelihood
H0 Value -38401.722
H1 Value -38401.722
Information Criteria
Akaike (AIC) 76821.443
Bayesian (BIC) 76880.098
Sample-Size Adjusted BIC 76851.499
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit
Value 0.000
Degrees of Freedom 0
P-Value 0.0000
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.000
90 Percent C.I. 0.000 0.000
Probability RMSEA <= .05 0.000
CFI/TLI
CFI 1.000
TLI 1.000
Chi-Square Test of Model Fit for the Baseline Model
Value 4113.328
Degrees of Freedom 5
P-Value 0.0000
SRMR (Standardized Root Mean Square Residual)
Value 0.000
Wald Test of Parameter Constraints
Value 1760.538
Degrees of Freedom 2
P-Value 0.0000
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
DETAIL2 11.987 0.439 27.303 0.000
DETAIL3 24.639 0.588 41.916 0.000
EXPER 0.424 0.016 26.133 0.000
EXPER ON
DETAIL2 7.998 0.365 21.903 0.000
DETAIL3 15.777 0.461 34.250 0.000
Intercepts
EXPER 124.231 0.309 402.529 0.000
OPINION 159.579 2.049 77.897 0.000
Residual Variances
EXPER 110.395 2.208 50.000 0.000
OPINION 145.601 2.912 49.999 0.000
QUALITY OF NUMERICAL RESULTS
Condition Number for the Information Matrix 0.125E-03
(ratio of smallest to largest eigenvalue)
TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Effects from DETAIL2 to OPINION
Total 15.382 0.447 34.403 0.000
Total indirect 3.395 0.202 16.786 0.000
Specific indirect 1
OPINION
EXPER
DETAIL2 3.395 0.202 16.786 0.000
Direct
OPINION
DETAIL2 11.987 0.439 27.303 0.000
Effects from DETAIL3 to OPINION
Total 31.335 0.564 55.559 0.000
Total indirect 6.696 0.322 20.776 0.000
Specific indirect 1
OPINION
EXPER
DETAIL3 6.696 0.322 20.776 0.000
Direct
OPINION
DETAIL3 24.639 0.588 41.916 0.000
DIAGRAM INFORMATION
Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram.
If running Mplus from the Mplus Diagrammer, the diagram opens automatically.
Interpretation of relative effects
When there is more than one arrow from detail (X) to exper (M), we now have relative effects. As in regression, we have coefficients for all but one of the categories of X. In this example, we used indicator (AKA dummy) coding. This is coding system is the one most commonly used with regression. The output shows the relative direct effects on X, the relative indirect effects on X, and the relative total effects on X. When interpreting relative effects, you need to remember which group (or category or level) of X is the reference group. In the example above, detail (X) is coded as into two dummy variables, detail2 and detail3, so the lowest values of detail (76 or less) is the reference group. The path for a1 is the mean of M1 – the mean of M0; the path for a2 is the mean of M2 – the mean of M0. The interpretation of the single coefficient from M to Y does not change even though there are multiple paths from X to M. The omnibus (AKA multi-degree-of-freedom) test of independent variable (detail) is given in the Mplus output at the end of the Model Fit Information section. This omnibus test is used to determine if the overall effect is statistically significant.
Let’s calculate the relative indirect effects and the relative total effects by hand. For the a2 path, 7.998*0.424 = 3.391152 (with rounding error). For the a2 path, 15.777*0.424 = 6.689448 (with rounding error). For the relative total effects, for the a2 path, we have 3.395 + 11.987 = 15.382 (with rounding error). For the a3 path, we have 6.697 + 24.638 = 31.327 (with rounding error). The total effect is 3.395 + 6.697 + 11.987 + 24.638 = 46.717.
Simple mediation model with covariates
Covariates can be added to any mediation model. The covariates can be either continuous or binary. In the example below, we include two covariates, one continuous (the variable ccovar) and one binary (the variable bcovar). Notice that both covariates are added to both equations. This is necessary for the direct effect and indirect effect(s) to sum to the total effect. The covariances between ccovar and bcovar must be set to 0; this is reasonable because we are not hypothesizing a relationship between the covariates.
Here is the diagram of the model.
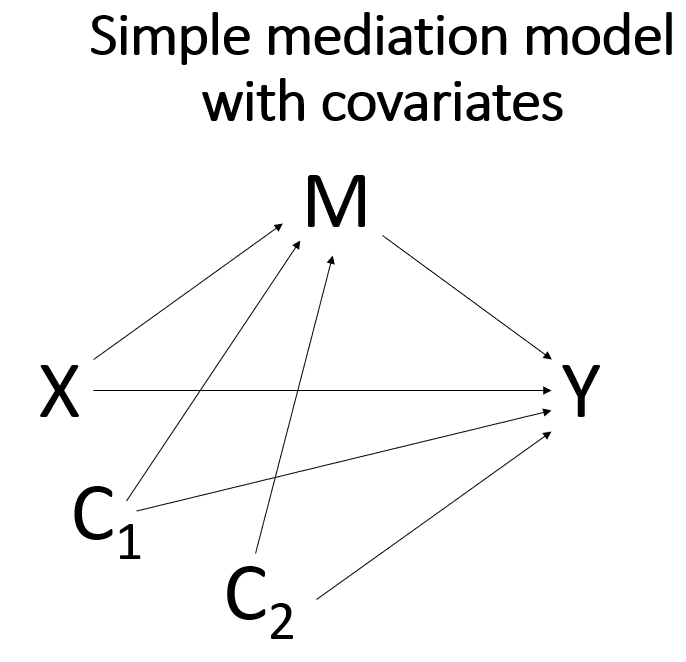Here is the Mplus code for this model.
title: simple mediation model with covariates
! predictor variable - x: detail
! mediator variable(s) - m: exper
! outcome variable - y: opinion
! covariates: bcovar and ccovar
data:
file is intro_mediation.dat;
variable:
names are detail exper impact opinion ccovar bcovar;
usevariables = detail exper opinion ccovar bcovar;
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on bcovar ccovar exper (b1);
opinion on bcovar ccovar detail (cprime);
exper on bcovar ccovar detail (a1);
model constraint:
new(a1b1 total);
a1b1 = a1*b1;
total = a1*b1 + cprime;
output:
cint(bcbootstrap);
Mplus VERSION 8.10
MUTHEN & MUTHEN
INPUT INSTRUCTIONS
title: simple mediation model with covariates
! predictor variable - x: detail
! mediator variable(s) - m: exper
! outcome variable - y: opinion
! covariates: bcovar and ccovar
data:
file is intro_mediation.dat;
variable:
names are detail exper impact opinion ccovar bcovar;
usevariables = detail exper opinion ccovar bcovar;
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on bcovar ccovar exper (b1);
opinion on bcovar ccovar detail (cprime);
exper on bcovar ccovar detail (a1);
model constraint:
new(a1b1 total);
a1b1 = a1*b1;
total = a1*b1 + cprime;
output:
cint(bcbootstrap);
INPUT READING TERMINATED NORMALLY
simple mediation model with covariates
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 5000
Number of dependent variables 2
Number of independent variables 3
Number of continuous latent variables 0
Observed dependent variables
Continuous
EXPER OPINION
Observed independent variables
DETAIL CCOVAR BCOVAR
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 1000
Convergence criterion 0.500D-04
Maximum number of steepest descent iterations 20
Number of bootstrap draws
Requested 10000
Completed 10000
Input data file(s)
intro_mediation.dat
Input data format FREE
UNIVARIATE SAMPLE STATISTICS
UNIVARIATE HIGHER-ORDER MOMENT DESCRIPTIVE STATISTICS
Variable/ Mean/ Skewness/ Minimum/ % with Percentiles
Sample Size Variance Kurtosis Maximum Min/Max 20%/60% 40%/80% Median
EXPER 131.845 0.034 86.303 0.02% 122.126 128.683 131.802
5000.000 136.500 -0.007 176.176 0.02% 134.746 141.553
OPINION 227.135 0.052 167.442 0.02% 213.095 222.728 227.098
5000.000 268.076 0.010 282.136 0.02% 231.195 240.820
DETAIL 82.884 -0.015 49.943 0.02% 74.894 80.601 82.934
5000.000 89.769 0.041 116.473 0.02% 85.382 90.652
CCOVAR 634.399 -0.013 439.832 0.02% 585.229 619.704 634.498
5000.000 3433.965 0.035 863.862 0.02% 649.125 682.934
BCOVAR 50.076 -0.006 42.474 0.02% 48.219 49.512 50.064
5000.000 4.985 -0.052 58.076 0.02% 50.637 51.952
THE MODEL ESTIMATION TERMINATED NORMALLY
MODEL FIT INFORMATION
Number of Free Parameters 7
Loglikelihood
H0 Value -37188.642
H1 Value -36354.576
Information Criteria
Akaike (AIC) 74391.283
Bayesian (BIC) 74436.904
Sample-Size Adjusted BIC 74414.660
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit
Value 1668.132
Degrees of Freedom 4
P-Value 0.0000
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.288
90 Percent C.I. 0.277 0.300
Probability RMSEA <= .05 0.000
CFI/TLI
CFI 0.797
TLI 0.645
Chi-Square Test of Model Fit for the Baseline Model
Value 8207.619
Degrees of Freedom 7
P-Value 0.0000
SRMR (Standardized Root Mean Square Residual)
Value 0.034
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
BCOVAR 0.169 0.003 65.427 0.000
CCOVAR 0.169 0.003 65.427 0.000
EXPER 0.165 0.015 10.919 0.000
DETAIL 0.169 0.003 65.427 0.000
EXPER ON
BCOVAR 0.097 0.002 48.722 0.000
CCOVAR 0.097 0.002 48.722 0.000
DETAIL 0.097 0.002 48.722 0.000
Intercepts
EXPER 57.726 1.522 37.922 0.000
OPINION 75.873 1.823 41.621 0.000
Residual Variances
EXPER 92.977 1.884 49.347 0.000
OPINION 106.416 2.174 48.939 0.000
New/Additional Parameters
A1B1 0.016 0.001 10.666 0.000
TOTAL 0.185 0.002 86.491 0.000
CONFIDENCE INTERVALS OF MODEL RESULTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
OPINION ON
BCOVAR 0.162 0.164 0.164 0.169 0.173 0.174 0.175
CCOVAR 0.162 0.164 0.164 0.169 0.173 0.174 0.175
EXPER 0.128 0.136 0.141 0.165 0.191 0.196 0.206
DETAIL 0.162 0.164 0.164 0.169 0.173 0.174 0.175
EXPER ON
BCOVAR 0.091 0.093 0.093 0.097 0.100 0.100 0.102
CCOVAR 0.091 0.093 0.093 0.097 0.100 0.100 0.102
DETAIL 0.091 0.093 0.093 0.097 0.100 0.100 0.102
Intercepts
EXPER 53.832 54.795 55.258 57.726 60.238 60.735 61.682
OPINION 71.142 72.234 72.837 75.873 78.866 79.422 80.483
Residual Variances
EXPER 88.274 89.403 89.979 92.977 96.231 96.813 97.756
OPINION 100.941 102.242 102.966 106.416 110.102 110.814 112.001
New/Additional Parameters
A1B1 0.012 0.013 0.014 0.016 0.018 0.019 0.020
TOTAL 0.179 0.180 0.181 0.185 0.188 0.189 0.190
DIAGRAM INFORMATION
Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram.
If running Mplus from the Mplus Diagrammer, the diagram opens automatically.
The interpretation of the path coefficients is just the same as before, except that we now add “holding the covariates constant” to the discussion of the path coefficients. Below is the diagram with the coefficients and standard errors.
From the diagram above, it should be clear that Mplus allows for multiple predictors in path models. (Remember that covariates and predictors are the same thing.) But should you run separate models for each predictor, or should you run a single that includes all of the predictors? The answer to that question depends on each individual research situation. Considerations include the research question to be addressed, the sample size, the number of tests that will results from each option (keeping an eye on the alpha inflation problem), etc.
Parallel mediation
In a parallel mediation model, you have two (or more) mediators, both of which are between the predictor and outcome. We will continue to use the variable exper as one mediator, and we will add the variable impact as the second mediator. In this example, there is no causal path between the two mediators, but one could be added if theory predicted a path to be there. Of course, now you have two sets of indirect effects: the indirect effect going through the first mediator (exper), and the indirect effect going through the second mediator (impact). Below is a path diagram describing the model.
title: parallel mediation model with all continuous variables
! predictor variable - x: detail
! mediator variable(s) m1: exper, m2: impact
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable: names are detail exper impact opinion ccovar bcovar;
usevariables = detail exper impact opinion;
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on exper (b1);
opinion on impact (b2);
opinion on detail (cdash);
exper on detail (a1);
impact on detail (a2);
model constraint:
new(a1b1 a2b2 totalind total);
a1b1 = a1*b1;
! specific indirect effect of x on y via m1
a2b2 = a2*b2;
! specific indirect effect of x on y via m2
totalind = a1*b1 + a2*b2;
! total indirect effect of x on y via m1, m2
total = a1*b1 + a2*b2 + cdash;
! total effect of x on y
output:
cint(bcbootstrap);
Mplus VERSION 8.10
MUTHEN & MUTHEN
INPUT INSTRUCTIONS
title: parallel mediation model with all continuous variables
! predictor variable - x: detail
! mediator variable(s) m1: exper, m2: impact
! outcome variable - y: opinion
data: file is intro_mediation.dat;
variable: names are detail exper impact opinion ccovar bcovar;
usevariables = detail exper impact opinion;
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on exper (b1);
opinion on impact (b2);
opinion on detail (cdash);
exper on detail (a1);
impact on detail (a2);
model constraint:
new(a1b1 a2b2 totalind total);
a1b1 = a1*b1;
! specific indirect effect of x on y via m1
a2b2 = a2*b2;
! specific indirect effect of x on y via m2
totalind = a1*b1 + a2*b2;
! total indirect effect of x on y via m1, m2
total = a1*b1 + a2*b2 + cdash;
! total effect of x on y
output:
cint(bcbootstrap);
INPUT READING TERMINATED NORMALLY
parallel mediation model with all continuous variables
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 5000
Number of dependent variables 3
Number of independent variables 1
Number of continuous latent variables 0
Observed dependent variables
Continuous
EXPER IMPACT OPINION
Observed independent variables
DETAIL
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 1000
Convergence criterion 0.500D-04
Maximum number of steepest descent iterations 20
Number of bootstrap draws
Requested 10000
Completed 10000
Input data file(s)
intro_mediation.dat
Input data format FREE
UNIVARIATE SAMPLE STATISTICS
UNIVARIATE HIGHER-ORDER MOMENT DESCRIPTIVE STATISTICS
Variable/ Mean/ Skewness/ Minimum/ % with Percentiles
Sample Size Variance Kurtosis Maximum Min/Max 20%/60% 40%/80% Median
EXPER 131.845 0.034 86.303 0.02% 122.126 128.683 131.802
5000.000 136.500 -0.007 176.176 0.02% 134.746 141.553
IMPACT 207.011 0.033 151.611 0.02% 193.931 203.017 206.750
5000.000 238.194 -0.012 266.428 0.02% 210.587 219.898
OPINION 227.135 0.052 167.442 0.02% 213.095 222.728 227.098
5000.000 268.076 0.010 282.136 0.02% 231.195 240.820
DETAIL 82.884 -0.015 49.943 0.02% 74.894 80.601 82.934
5000.000 89.769 0.041 116.473 0.02% 85.382 90.652
THE MODEL ESTIMATION TERMINATED NORMALLY
MODEL FIT INFORMATION
Number of Free Parameters 11
Loglikelihood
H0 Value -56407.755
H1 Value -55878.321
Information Criteria
Akaike (AIC) 112837.510
Bayesian (BIC) 112909.200
Sample-Size Adjusted BIC 112874.245
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit
Value 1058.868
Degrees of Freedom 1
P-Value 0.0000
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.460
90 Percent C.I. 0.437 0.483
Probability RMSEA <= .05 0.000
CFI/TLI
CFI 0.901
TLI 0.407
Chi-Square Test of Model Fit for the Baseline Model
Value 10714.936
Degrees of Freedom 6
P-Value 0.0000
SRMR (Standardized Root Mean Square Residual)
Value 0.098
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
EXPER 0.003 0.014 0.185 0.853
IMPACT 0.602 0.012 49.057 0.000
DETAIL 0.585 0.018 32.228 0.000
EXPER ON
DETAIL 0.614 0.015 41.117 0.000
IMPACT ON
DETAIL 1.026 0.018 57.803 0.000
Intercepts
EXPER 80.965 1.239 65.322 0.000
IMPACT 122.003 1.473 82.812 0.000
OPINION 53.636 1.810 29.626 0.000
Residual Variances
EXPER 102.672 2.086 49.216 0.000
IMPACT 143.765 2.804 51.267 0.000
OPINION 85.605 1.713 49.975 0.000
New/Additional Parameters
A1B1 0.002 0.009 0.185 0.853
A2B2 0.618 0.016 37.598 0.000
TOTALIND 0.619 0.016 39.181 0.000
TOTAL 1.204 0.017 69.236 0.000
CONFIDENCE INTERVALS OF MODEL RESULTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
OPINION ON
EXPER -0.033 -0.025 -0.020 0.003 0.027 0.032 0.040
IMPACT 0.571 0.578 0.582 0.602 0.623 0.626 0.634
DETAIL 0.537 0.548 0.554 0.585 0.614 0.620 0.631
EXPER ON
DETAIL 0.576 0.584 0.589 0.614 0.638 0.643 0.652
IMPACT ON
DETAIL 0.982 0.992 0.997 1.026 1.056 1.062 1.073
Intercepts
EXPER 77.783 78.585 78.939 80.965 82.996 83.385 84.221
IMPACT 118.026 118.962 119.486 122.003 124.335 124.760 125.629
OPINION 48.855 49.999 50.575 53.636 56.543 57.128 58.224
Residual Variances
EXPER 97.460 98.715 99.329 102.672 106.233 106.884 107.956
IMPACT 136.577 138.445 139.337 143.765 148.579 149.445 151.028
OPINION 81.375 82.358 82.899 85.605 88.547 89.055 90.166
New/Additional Parameters
A1B1 -0.021 -0.015 -0.012 0.002 0.017 0.020 0.025
A2B2 0.577 0.586 0.591 0.618 0.645 0.651 0.662
TOTALIND 0.580 0.589 0.594 0.619 0.646 0.651 0.661
TOTAL 1.159 1.170 1.175 1.204 1.233 1.239 1.250
DIAGRAM INFORMATION
Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram.
If running Mplus from the Mplus Diagrammer, the diagram opens automatically.
The interpretation of the path coefficients is the same as in previous models, except that now we include “holding both mediators constant” when discussing the direct effect or “holding the other mediator constant” when discussing one of the mediators. Looking at the last part of the output above, we see that we are given the total indirect effect, 0.580, as well as the indirect effect via exper, 0.002, and the indirect effect via impact, 0.816.
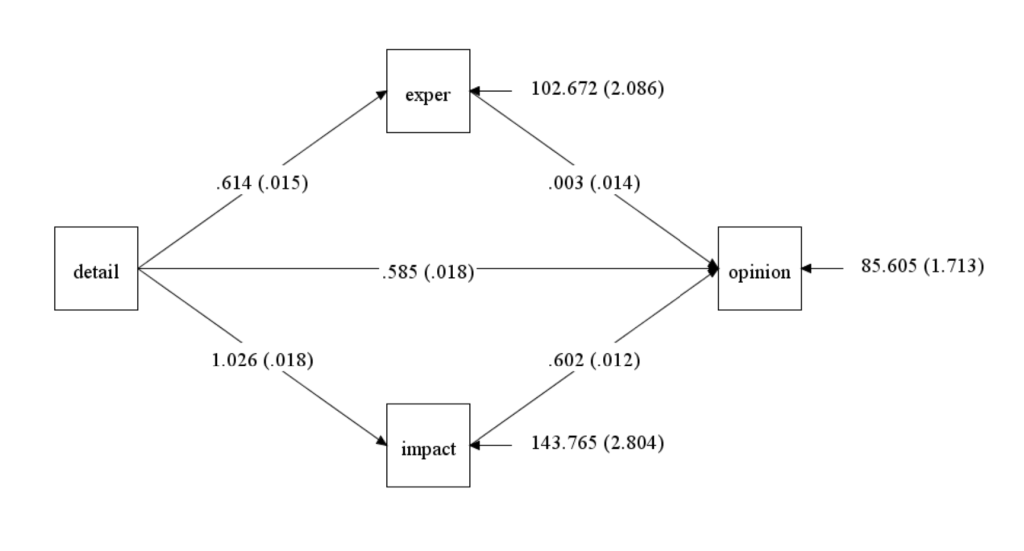
Serial mediation
In a serial mediation model, the mediators are ordered between the predictor and the outcome. There may or may not be causal arrows between the mediators; that should be determined by theory.
title: serial mediation model with all continuous variables
! predictor variable - x: detail
! mediator variable(s) - m1: exper, m2: impact
! outcome variable - y: opinion
data:
file is intro_mediation.dat;
variable: names are detail exper impact opinion ccovar bcovar;
usevariables = detail exper impact opinion;
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on detail exper impact;
exper impact on detail;
impact on exper;
model indirect:
opinion ind impact exper detail;
opinion ind exper detail;
opinion ind impact detail;
output:
cint(bcbootstrap);
Mplus VERSION 8.10
MUTHEN & MUTHEN
INPUT INSTRUCTIONS
title: serial mediation model with all continuous variables
! predictor variable - x: detail
! mediator variable(s) - m1: exper, m2: impact
! outcome variable - y: opinion
data:
file is intro_mediation.dat;
variable: names are detail exper impact opinion ccovar bcovar;
usevariables = detail exper impact opinion;
analysis:
type = general;
estimator = ml;
bootstrap = 10000;
model:
opinion on detail exper impact;
exper impact on detail;
impact on exper;
model indirect:
opinion ind impact exper detail;
opinion ind exper detail;
opinion ind impact detail;
output:
cint(bcbootstrap);
INPUT READING TERMINATED NORMALLY
serial mediation model with all continuous variables
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 5000
Number of dependent variables 3
Number of independent variables 1
Number of continuous latent variables 0
Observed dependent variables
Continuous
EXPER IMPACT OPINION
Observed independent variables
DETAIL
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 1000
Convergence criterion 0.500D-04
Maximum number of steepest descent iterations 20
Number of bootstrap draws
Requested 10000
Completed 10000
Input data file(s)
intro_mediation.dat
Input data format FREE
UNIVARIATE SAMPLE STATISTICS
UNIVARIATE HIGHER-ORDER MOMENT DESCRIPTIVE STATISTICS
Variable/ Mean/ Skewness/ Minimum/ % with Percentiles
Sample Size Variance Kurtosis Maximum Min/Max 20%/60% 40%/80% Median
EXPER 131.845 0.034 86.303 0.02% 122.126 128.683 131.802
5000.000 136.500 -0.007 176.176 0.02% 134.746 141.553
IMPACT 207.011 0.033 151.611 0.02% 193.931 203.017 206.750
5000.000 238.194 -0.012 266.428 0.02% 210.587 219.898
OPINION 227.135 0.052 167.442 0.02% 213.095 222.728 227.098
5000.000 268.076 0.010 282.136 0.02% 231.195 240.820
DETAIL 82.884 -0.015 49.943 0.02% 74.894 80.601 82.934
5000.000 89.769 0.041 116.473 0.02% 85.382 90.652
THE MODEL ESTIMATION TERMINATED NORMALLY
MODEL FIT INFORMATION
Number of Free Parameters 12
Loglikelihood
H0 Value -55878.321
H1 Value -55878.321
Information Criteria
Akaike (AIC) 111780.643
Bayesian (BIC) 111858.849
Sample-Size Adjusted BIC 111820.717
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit
Value 0.000
Degrees of Freedom 0
P-Value 0.0000
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.000
90 Percent C.I. 0.000 0.000
Probability RMSEA <= .05 0.000
CFI/TLI
CFI 1.000
TLI 1.000
Chi-Square Test of Model Fit for the Baseline Model
Value 10714.936
Degrees of Freedom 6
P-Value 0.0000
SRMR (Standardized Root Mean Square Residual)
Value 0.000
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
OPINION ON
DETAIL 0.585 0.018 32.229 0.000
EXPER 0.003 0.014 0.185 0.854
IMPACT 0.602 0.012 49.056 0.000
EXPER ON
DETAIL 0.614 0.015 41.116 0.000
IMPACT ON
DETAIL 0.708 0.018 38.612 0.000
EXPER 0.517 0.015 34.313 0.000
Intercepts
EXPER 80.964 1.239 65.320 0.000
IMPACT 80.149 1.804 44.425 0.000
OPINION 53.639 1.810 29.627 0.000
Residual Variances
EXPER 102.672 2.086 49.219 0.000
IMPACT 116.328 2.236 52.030 0.000
OPINION 85.605 1.713 49.976 0.000
TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Effects from DETAIL to OPINION
Sum of indirect 0.619 0.016 39.180 0.000
Specific indirect 1
OPINION
IMPACT
EXPER
DETAIL 0.191 0.008 23.015 0.000
Specific indirect 2
OPINION
EXPER
DETAIL 0.002 0.009 0.184 0.854
Specific indirect 3
OPINION
IMPACT
DETAIL 0.427 0.014 30.605 0.000
CONFIDENCE INTERVALS OF MODEL RESULTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
OPINION ON
DETAIL 0.537 0.548 0.554 0.585 0.614 0.620 0.631
EXPER -0.033 -0.025 -0.020 0.003 0.027 0.032 0.040
IMPACT 0.571 0.578 0.582 0.602 0.623 0.626 0.634
EXPER ON
DETAIL 0.576 0.584 0.589 0.614 0.638 0.643 0.652
IMPACT ON
DETAIL 0.663 0.673 0.679 0.708 0.739 0.745 0.758
EXPER 0.478 0.488 0.492 0.517 0.542 0.546 0.556
Intercepts
EXPER 77.783 78.585 78.939 80.964 82.996 83.385 84.221
IMPACT 75.382 76.526 77.151 80.149 83.131 83.711 84.736
OPINION 48.859 50.005 50.578 53.639 56.546 57.147 58.224
Residual Variances
EXPER 97.459 98.716 99.332 102.672 106.233 106.883 107.959
IMPACT 110.549 112.083 112.753 116.328 120.092 120.748 122.154
OPINION 81.375 82.358 82.899 85.605 88.547 89.054 90.166
CONFIDENCE INTERVALS OF TOTAL, TOTAL INDIRECT, SPECIFIC INDIRECT, AND DIRECT EFFECTS
Lower .5% Lower 2.5% Lower 5% Estimate Upper 5% Upper 2.5% Upper .5%
Effects from DETAIL to OPINION
Sum of indirect 0.580 0.589 0.594 0.619 0.646 0.651 0.661
Specific indirect 1
OPINION
IMPACT
EXPER
DETAIL 0.171 0.176 0.178 0.191 0.205 0.208 0.214
Specific indirect 2
OPINION
EXPER
DETAIL -0.021 -0.015 -0.012 0.002 0.017 0.020 0.025
Specific indirect 3
OPINION
IMPACT
DETAIL 0.392 0.400 0.403 0.427 0.450 0.454 0.463
DIAGRAM INFORMATION
Use View Diagram under the Diagram menu in the Mplus Editor to view the diagram.
If running Mplus from the Mplus Diagrammer, the diagram opens automatically.
Diagram output
d:\data\seminars\intro_mediation_mplus\example14.dgm
A few cautions
Total effect: The total effect is not always a good way of thinking about the predictor’s (X) effect on the ultimate outcome (Y). In many analyses, the indirect effect and the direct effect have different signs (i.e., one is positive and the other is negative). When this happens, the total effect may be close to 0. In other analyses, the indirect effect may be well-estimated (meaning that the standard error is small and the confidence interval is narrow), but the direct effect may not be so well estimated. When these are added together, the total effect may be poorly estimated (meaning it too has a great deal of sampling variability). Also, the power to detect a difference from 0 is different for the indirect and total effects. Ratio of the indirect effect to the total effect: Historically, the proportion mediated was defined as the indirect effect divided by the direct effect, or ab/c or ab/(c-prime + ab). From this, it is clear that the closer the ratio is to 1 the effect of X on Y operated through M; the closter the ratio is to 0, the less of the effect is mediated via M. There are some problems with this approach. First, a proportion is, by definition, a value between 0 and 1, but the indirect effect divided by the direct effect can be negative or larger than 1. Secondly, proportion mediated is highly variable between samples of data. In other words, this value typically has a very wide confidence interval, even when other values calcuated in the mediation analysis have narrow confidence intervals. The ratio of the indirect effect to the direct effect is just a variation on the idea of the ratio of the indirect effect to the total effect. One problem with this ratio is that, as the direct effect approaches 0, even a small indirect effect will be large relative to the direct effect. This value also suffers from the problem of high sample-to-sample variability.
Missing data
Missing data is a common issue when running path models. The nature of the missingness is critical to knowing how to handle the missing values. In the examples below, we assume that the data are missing completely at random (MCAR). When the data are missing completely at random on the outcome variable, the mediator variable, or both the outcome and mediator variables, only one additional line of code is needed. In the Data command, a Missing statement is needed. This statement tells Mplus which value(s) indicate missing in the data file. By default, Mplus will use Full Information Maximum Likelihood (FIML) to handle the missing data. When the independent variable has missing values, another line is needed in the Model command. This line is simply the name of the independent variable given in square brackets. This requests that Mplus calculate the mean of the independent variable, thus treating it as an outcome.
Here is the dataset with MCAR missing on only the outcome variable: intro_mediation_DV_missing.
Here is the Mplus syntax:
! predictor variable - x: detail ! mediator variable(s) - m: exper ! outcome variable - y: opinion title: missing data on DV only; data: file is intro_mediation_DV_missing.txt; variable: names are detail exper impact opinion ccovar bcovar; usevariables = detail exper opinion; analysis: type = general; estimator = ml; bootstrap = 10000; model: opinion on exper (b1); opinion on detail (cdash); exper on detail (a1); model indirect: opinion ind detail; output: cint(bcbootstrap);
Here is the dataset with MCAR missing on only the mediator variable: intro_mediation_med_missing.
Here is the Mplus syntax:
! predictor variable - x: detail ! mediator variable(s) - m: exper ! outcome variable - y: opinion title: missing data on MV only; data: file is intro_mediation_med_missing.txt; variable: names are detail exper impact opinion ccovar bcovar; usevariables = detail exper opinion; analysis: type = general; estimator = ml; bootstrap = 10000; model: opinion on exper; opinion on detail; exper on detail; model indirect: opinion ind detail; output: cint(bcbootstrap);
Here is the dataset with MCAR missing on both the outcome and mediator vairable: intro_mediation_DV_med_missing.
Here is the Mplus syntax:
! predictor variable - x: detail ! mediator variable(s) - m: exper ! outcome variable - y: opinion title: missing data on DV and MV; data: file is intro_mediation_DV_med_missing.txt; variable: names are detail exper impact opinion ccovar bcovar; usevariables = detail exper opinion; missing are all (-9999); analysis: type = general; estimator = ml; bootstrap = 10000; model: opinion on exper; opinion on detail; exper on detail; model indirect: opinion ind detail; output: cint(bcbootstrap);
Here is the dataset with MCAR missing on the independent variable: intro_mediation_IV_missing.
Here is the Mplus syntax:
! predictor variable - x: detail ! mediator variable(s) - m: exper ! outcome variable - y: opinion title: missing data on IV only; data: file is intro_mediation_IV_missing.txt; variable: names are detail exper impact opinion ccovar bcovar; usevariables = detail exper opinion; missing are all (-9999); analysis: type = general; estimator = ml; bootstrap = 10000; model: opinion on exper; opinion on detail; exper on detail; [detail]; model indirect: opinion ind detail; output: cint(bcbootstrap);
Criteria for making causal claims
The criteria for making causal claims has changed greatly in the last 10-15 years. Gone are the days of Baron and Kenny and the causal steps approach. Hayes provides a thoughtful explanation of why this method, that was so widely used for 20 years, is no longer acceptable. The work of Judea Pearl and Tyler VanderWeele have been very influential in this change. A complete discussion of the current set of criteria needed to claim causality is beyond the scope of this workshop, but a few important points will be made. First, and perhaps most obvious, the predictor must precede the mediator which must precede the outcome in time. In other words, the cause must come before the effect. This means that cross-sectional data are usually inappropriate for mediation analysis, because all of the data (for X, M and Y) are collected at the same time, so there is no way to guarantee that the cause happened before the effect. Second, just because you used a particular variable as the mediator does not mean that it is the only mediator. Perhaps another variable is the real mediator, and the variable you are using is just correlated with the real mediator. Or perhaps a variable that is not in your model, and maybe not even in your dataset, causes both the mediator and the outcome. When thinking about experiments and causality, most researchers immediately think of randomly assigning subjects to experimental groups or conditions; however, such assignment does not mean that mediator causes the outcome.
In his paper Mediation Analysis: A Practitioner’s Guide (2015), VanderWeele lists four assumptions that need to be assessed so that the direct and indirect effects are interpretable.
- no confounding between X and Y
- no confounding between M and Y
- no confounding between X and M
- no confounding between M and Y that is itself affected by X.
As you can see, many of these assumptions are not testable using the dataset at hand, but rather must be made on a logical basis.
With respect to writing up a mediation analysis, please be sure to check on the current guidelines. They have changed quite a bit in the last few years, and they will probably continue to change for some time to come.
References
Geiser, Christian. (2013). Data Analysis with Mplus. New York: Guilford Press.
Hayes, Andrew F. (2022). Introduction to Mediation, Moderation and Conditional Process Analysis: A Regression-Based Approach, Third Edition. New York: Guildford Press.
Muthen, Bengt O., Muthen, Linda K. and Asparouhov, Tihomir. (2016). Regression and Mediation Analysis Using Mplus. Los Angeles, CA: Muthen & Muthen.
Chris Stride: Figure It Out https://www.figureitout.org.uk/