Confirmatory factor analysis (CFA) is a measurement model that estimates continuous latent variables based on observed indicator variables (also called manifest variables). The observed indicator variables may be either categorical or continuous. One way to think about confirmatory factor analysis is that each case has a “true score” on the (continuous) latent variable, and that each of the observed values is a result of that “true score” plus measurement error. The model attempts to estimate that “true score” based on the relationships among the observed values.
Mplus version 5.2 was used for these examples.
1.0 A Measurement Model for a Single Latent Variable
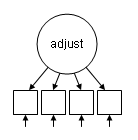
The examples on this page use data on the attributes of a group of students (see note at the bottom of the page for information on the source). The dataset (https://stats.idre.ucla.edu/wp-content/uploads/2016/02/wordland_data.dat) contains 12 observed variables, which can be used to estimate four latent variables. The 12 observed variables have all been standardized to have a mean of zero and a standard deviation of one. The four latent variables are students’ family “risk factors” (family), cognitive ability based on standardized tests (cognitive/cog), achievement, that is grades, in school (achieve), and classroom adjustment based on ratings by each student’s teacher (adjust). As a first step, we will estimate a model for a single latent variable. The diagram below shows the measurement model for the adjustment latent variable (adjust). The observed variables, represented as empty boxes are motivation (motiv), extraversion (extra), harmony (harm), and stability (stabi).
The input file shown below estimates the model described above. In the model: command, the keyword by indicates that the latent variable named before the by is measured by the manifest variables listed after it.
Title: Measurement model for one latent variable
Data:
File is worland_data.dat ;
Variable:
Names are ppsych ses verbal vissp mem read arith spell motiv extra harm stabi;
usevariables are motiv extra harm stabi;
Model:
adjust by motiv extra harm stabi;
The output based on this input file is shown below.
INPUT READING TERMINATED NORMALLY
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 500
Number of dependent variables 4
Number of independent variables 0
Number of continuous latent variables 1
Observed dependent variables
Continuous
MOTIV EXTRA HARM STABI
Continuous latent variables
ADJUST
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 1000
Convergence criterion 0.500D-04
Maximum number of steepest descent iterations 20
Maximum number of iterations for H1 2000
Convergence criterion for H1 0.100D-03
Input data file(s)
worland_data.dat
Input data format FREE
SUMMARY OF DATA
Number of missing data patterns 1
COVARIANCE COVERAGE OF DATA
Minimum covariance coverage value 0.100
PROPORTION OF DATA PRESENT
Covariance Coverage
MOTIV EXTRA HARM STABI
________ ________ ________ ________
MOTIV 1.000
EXTRA 1.000 1.000
HARM 1.000 1.000 1.000
STABI 1.000 1.000 1.000 1.000
THE MODEL ESTIMATION TERMINATED NORMALLY
TESTS OF MODEL FIT
Chi-Square Test of Model Fit
Value 218.606
Degrees of Freedom 2
P-Value 0.0000
Chi-Square Test of Model Fit for the Baseline Model
Value 927.867
Degrees of Freedom 6
P-Value 0.0000
CFI/TLI
CFI 0.765
TLI 0.295
Loglikelihood
H0 Value -2481.245
H1 Value -2371.942
Information Criteria
Number of Free Parameters 12
Akaike (AIC) 4986.489
Bayesian (BIC) 5037.065
Sample-Size Adjusted BIC 4998.976
(n* = (n + 2) / 24)
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.465
90 Percent C.I. 0.414 0.519
Probability RMSEA <= .05 0.000
SRMR (Standardized Root Mean Square Residual)
Value 0.113
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
ADJUST BY
MOTIV 1.000 0.000 999.000 999.000
EXTRA 0.211 0.053 4.002 0.000
HARM 0.954 0.056 17.086 0.000
STABI 0.722 0.050 14.582 0.000
Intercepts
MOTIV 0.000 0.045 0.000 1.000
EXTRA 0.000 0.045 0.000 1.000
HARM 0.000 0.045 0.000 1.000
STABI 0.000 0.045 0.000 1.000
Variances
ADJUST 0.811 0.074 11.016 0.000
Residual Variances
MOTIV 0.187 0.041 4.505 0.000
EXTRA 0.962 0.061 15.693 0.000
HARM 0.259 0.040 6.499 0.000
STABI 0.575 0.041 14.055 0.000
QUALITY OF NUMERICAL RESULTS
Condition Number for the Information Matrix 0.385E-01
(ratio of smallest to largest eigenvalue)
In the MODEL RESULTS section of the above output, the first block of estimates labeled ADJUST BY contains the loadings for the relationship between the individual items and the latent variable. All of the loadings (shown in the Estimates column) are positive, indicating a positive relationship between the latent variable adjustment and our four observed measures of adjustment. In the far right column, we can also see that each of the loadings is significantly different from zero. The subsequent blocks show the intercepts for the observed variables (labeled Intercepts), the variance of the latent variable adjust (labeled Variances), and the estimates of the error variance for each of the observed variables (labeled Residual Variances).
2.0 A Measurement Model with Multiple (Correlated) Latent Variables
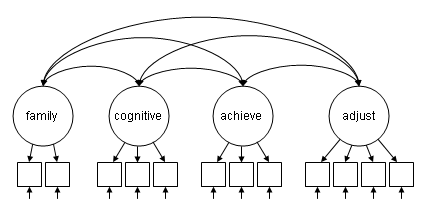
In this example, the model estimates all four latent variables at the same time, and allows the latent variables to covary, without imposing additional structure. A model with all of the latent variables allowed to covary is often run as a precursor to a model with a more specific set of relationships among the latent variables. The desired model is shown in the diagram below. Note that the curved double-headed arrows denote covariances.
The input file for this model is similar to the last. This model contains instructions for four latent variables, each measured by a series of observed variables (e.g. family by ppsych ses;).
Title: Measurement model with correlations Data: File is worland_data.dat ; Variable: Names are ppsych ses verbal vissp mem read arith spell motiv extra harm stabi; Model: adjust by motiv extra harm stabi; family by ppsych ses; cog by verbal vissp mem; achieve by read arith spell;
The output based on this input file is shown below.
INPUT READING TERMINATED NORMALLY
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 500
Number of dependent variables 12
Number of independent variables 0
Number of continuous latent variables 4
Observed dependent variables
Continuous
PPSYCH SES VERBAL VISSP MEM READ
ARITH SPELL MOTIV EXTRA HARM STABI
Continuous latent variables
FAMILY COG ACHIEVE ADJUST
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 1000
Convergence criterion 0.500D-04
Maximum number of steepest descent iterations 20
Input data file(s)
worland_data.dat
Input data format FREE
THE MODEL ESTIMATION TERMINATED NORMALLY
TESTS OF MODEL FIT
Chi-Square Test of Model Fit
Value 600.106
Degrees of Freedom 48
P-Value 0.0000
Chi-Square Test of Model Fit for the Baseline Model
Value 4124.707
Degrees of Freedom 66
P-Value 0.0000
CFI/TLI
CFI 0.864
TLI 0.813
Loglikelihood
H0 Value -6745.325
H1 Value -6445.272
Information Criteria
Number of Free Parameters 42
Akaike (AIC) 13574.649
Bayesian (BIC) 13751.663
Sample-Size Adjusted BIC 13618.352
(n* = (n + 2) / 24)
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.152
90 Percent C.I. 0.141 0.163
Probability RMSEA <= .05 0.000
SRMR (Standardized Root Mean Square Residual)
Value 0.063
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
FAMILY BY
PPSYCH 1.000 0.000 999.000 999.000
SES -1.107 0.115 -9.657 0.000
COG BY
VERBAL 1.000 0.000 999.000 999.000
VISSP 0.833 0.045 18.393 0.000
MEM 0.972 0.044 22.326 0.000
ACHIEVE BY
READ 1.000 0.000 999.000 999.000
ARITH 0.842 0.034 24.840 0.000
SPELL 0.954 0.027 35.622 0.000
ADJUST BY
MOTIV 1.000 0.000 999.000 999.000
EXTRA 0.233 0.048 4.813 0.000
HARM 0.857 0.042 20.295 0.000
STABI 0.662 0.045 14.615 0.000
FAMILY WITH
COG -0.411 0.046 -8.852 0.000
ACHIEVE -0.363 0.044 -8.151 0.000
ADJUST -0.245 0.040 -6.099 0.000
COG WITH
ACHIEVE 0.740 0.056 13.305 0.000
ADJUST 0.508 0.048 10.510 0.000
ACHIEVE WITH
ADJUST 0.567 0.051 11.102 0.000
Intercepts
PPSYCH 0.000 0.045 0.000 1.000
SES 0.000 0.045 0.000 1.000
VERBAL 0.000 0.045 0.000 1.000
VISSP 0.000 0.045 0.000 1.000
MEM 0.000 0.045 0.000 1.000
READ 0.000 0.045 0.000 1.000
ARITH 0.000 0.045 0.000 1.000
SPELL 0.000 0.045 0.000 1.000
MOTIV 0.000 0.045 0.000 1.000
EXTRA 0.000 0.045 0.000 1.000
HARM 0.000 0.045 0.000 1.000
STABI 0.000 0.045 0.000 1.000
Variances
FAMILY 0.379 0.061 6.201 0.000
COG 0.739 0.063 11.678 0.000
ACHIEVE 0.897 0.064 14.002 0.000
ADJUST 0.901 0.070 12.842 0.000
Residual Variances
PPSYCH 0.619 0.053 11.681 0.000
SES 0.534 0.055 9.652 0.000
VERBAL 0.259 0.024 10.967 0.000
VISSP 0.485 0.035 13.679 0.000
MEM 0.300 0.026 11.643 0.000
READ 0.101 0.014 7.142 0.000
ARITH 0.362 0.027 13.612 0.000
SPELL 0.181 0.016 11.387 0.000
MOTIV 0.097 0.032 3.049 0.002
EXTRA 0.949 0.060 15.702 0.000
HARM 0.336 0.033 10.318 0.000
STABI 0.604 0.042 14.269 0.000
QUALITY OF NUMERICAL RESULTS
Condition Number for the Information Matrix 0.320E-02
(ratio of smallest to largest eigenvalue)
Looking at the MODEL RESULTS section of the output, the first four blocks of estimates give the loadings for the relationship between the latent variables and the observed variables (e.g. FAMILY BY). After the loadings for the four latent variables, the covariances between the latent variables (indicated using the keyword WITH) are shown. Looking at the first block of covariances (labeled FAMILY WITH) we see that the latent variable family (i.e. family risk factors) has a negative relationship with cog (cognitive ability), achieve (academic achievement), and adjust (classroom adjustment). Note that our input file does not explicitly include these covariances, Mplus includes them by default.
3.0 Saving Factor Scores
In addition to the output file produced by Mplus, it is possible to save factor scores for each case in a text file that can later be used by Mplus or read into another statistical package. To do this the savedata: command is added to the input file. The file option gives the name of the file in which the factor scores should be saved (i.e. scores.txt). Whenever the file option is used, all of the variables used in the analysis are saved in an external file. The save = fscores; option specifies that the factor scores should be saved, in addition to the variables used in estimation. Additional variables that were not used in the analysis, but which you wish to include in the saved file, for example, an id variable, can be included by adding the auxiliary option (e.g. auxiliary = id;) to the variable: command.
Title: Saving Factor Scores
Data:
File is worland_data.dat ;
Variable:
Names are ppsych ses verbal vissp mem read arith spell motiv extra harm stabi;
Model:
adjust by motiv extra harm stabi;
family by ppsych ses;
cog by verbal vissp mem;
achieve by read arith spell;
Savedata:
file is scores.txt;
save = fscores;
The output file for this model contains all of the information contained in the output for the previous model, plus additional output associated with the savedata: command. This additional output appears towards the end of the output file, and is shown below.
SAVEDATA INFORMATION
Order and format of variables
PPSYCH F10.3
SES F10.3
VERBAL F10.3
VISSP F10.3
MEM F10.3
READ F10.3
ARITH F10.3
SPELL F10.3
MOTIV F10.3
EXTRA F10.3
HARM F10.3
STABI F10.3
ADJUST F10.3
FAMILY F10.3
COG F10.3
ACHIEVE F10.3
Save file
scores.txt
Save file format
16F10.3
Save file record length 5000
The additional output associated with the savedata: command lists the variables in the order in which they appear in the saved dataset. Note that the 12 observed variables used in estimation are listed first, followed by four variables containing the factor scores associated with each of the four latent variables. Below the list of variables the name of the file, and information on the format of the file are shown.
The file class.txt is a text file that can be read by a large number of programs. The first few lines of this file are shown below. This file contains 16 variables, each in its own column. Based on the information in the output file, we know that the first 12 columns contain each student’s value on the 12 observed variables, and the final four columns are each student’s factor score for each of the four latent variables.
-1.780 0.477 -0.790 -0.363 0.311 -0.349 -0.999 -0.657 -0.791 -0.496 -0.508 -0.314 -0.693 -0.318 -0.239 -0.509
0.701 -0.605 -0.955 -0.769 -0.398 -0.452 0.820 0.878 0.175 -0.240 -0.416 0.352 0.055 0.452 -0.421 -0.013
2.373 -1.697 -0.130 -0.391 0.146 -0.482 0.753 -0.569 1.447 0.293 -0.454 0.407 0.926 0.809 -0.333 -0.262
0.149 0.140 1.752 2.141 -0.189 -0.314 0.573 -0.292 -0.117 -0.174 -0.567 0.260 -0.134 -0.315 0.536 0.011
-0.599 -1.838 0.675 -0.144 -0.246 -0.201 -0.062 -0.102 -0.422 0.366 -1.007 -0.603 -0.498 0.253 -0.069 -0.123
Data Source
The data for these examples is based on a correlation matrix published in Worland et al. (1984). Although the correlation matrix would have been sufficient to specify these models, 500 cases were randomly drawn from the distribution described by the published correlation matrix. The models below do not necessarily match those specified in Worland et al. (1984), they are intended as examples only.
Worland, Julien, David G. Weeks, Cynthia L. Janes, and Barbara D. Strock (1984) Intelligence, classroom behavior, and academic achievement in children at high and low risk for psychopathology: A structural equation analysis. Journal of Abnormal Child Psychology Vol. 12, No. 3, pp. 437-454.