Purpose: The following page will explain how to perform a latent class analysis in Mplus, one with categorical variables and the other with a mix of categorical and continuous variables. A mixture model with categorical variables is called latent class analysis, whereas a mixture model with only continuous variables is called a latent profile analysis (Oberski, 2016).
Note: Mplus version 8 was used for these examples. Download all the files for this portion of this seminar.
1.0 Basic latent class analysis model
Latent class analysis is used to classify individuals into homogeneous subgroups. Individual differences in observed item response patterns are explained by differences in latent class membership (Geiser, 2013). For the case with only dichotomous variables \(X=\{0,1\}\), the latent class analysis (LCA) model for a single item can be written as:
$$ P(X_{vi} =1) = \sum_{g=1}^{G} \pi_{g} \pi_{ig} $$
where \(P(X_{vi}=1)\) denotes the unconditional probability that a randomly selected individual \(v\) obtained a score of \(X=1\) on item \(i\), \((i=1,\cdots,I)\) and the parameter
$$ \pi_{ig} = P(X_{vi} = 1 | G = g) $$
is the conditional solution probability. Since the sum of the two conditional probabilities equals one,
$$ P(X_{vi} = 0 | G = g) = 1-\pi_{ig}. $$
The class size parameter \(\pi_g\) indicates the unconditional probability of belonging to latent class \(g\), \((g = 1, \cdots, G)\), and the sum of all class-size parameters is 1, i.e.,
$$ \sum_{g=1}^{G} \pi_{g} = 1. $$
We will illustrate a simple latent class analysis (LCA) using the mplus73recode.dat dataset and see if we can identify two classes based on four binary variables. For example, the variable u1 indicates whether the student was in honors math in seventh grade (1=yes; 0=no); the variable u2 indicates whether the student was in honors math in eighth grade; rc3 indicates whether the student was in honors math in ninth grade; and rc4 indicates whether the student was in honors math in tenth grade. We specify that two latent classes should be extracted, and we expect that these classes will differentiate students who have a particularly high aptitude in math from those who do not.
In the syntax below, the title statement is used to remind us what analysis we are running. The data statement tells Mplus where the text data file is located. The variables statement tells Mplus the names of the variables in the text file (these names are not listed at the top of the text file); the usevariables statement tells Mplus which variables we will be using in this analysis; the classes statement indicates the number of classes we wish to extract; and the categorical statement tells Mplus which variables are categorical.
By specifying mixture on the analysis statement, we tell Mplus that our data are a mixture of two subpopulations. We use the savedata statement save to class membership information to a text file called lca73classes.txt. We will save the class probabilities (cprob) in this file, and the file will be a free format text file. We can open this file in another program and look at the class membership probabilities and class assignment. The plot statement requests that we would like get all possible plots (type 3), graphs where the values are connected by a line. The (*) at the end of the series statement requests integer values starting with 0 and increasing by 1.
title: This is an example of LCA with binary latent class indicators
data:
file is mplus73recode.dat;
variable:
names are u1-u4 rc3 rc4 x1-x10;
usevariables = u1 u2 rc3 rc4;
classes = c (2);
categorical = u1 u2 rc3 rc4;
analysis:
type=mixture;
savedata:
file is lca73classes.txt ;
save is cprob;
format is free;
plot:
type is plot3;
series is u1 u2 rc3 rc4(*);
Below is the resulting output.
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 500
Number of dependent variables 4
Number of independent variables 0
Number of continuous latent variables 0
Number of categorical latent variables 1
Observed dependent variables
Binary and ordered categorical (ordinal)
U1 U2 RC3 RC4
Categorical latent variables
C
Estimator MLR
Information matrix OBSERVED
Optimization Specifications for the Quasi-Newton Algorithm for
Continuous Outcomes
Maximum number of iterations 100
Convergence criterion 0.100D-05
Optimization Specifications for the EM Algorithm
Maximum number of iterations 500
Convergence criteria
Loglikelihood change 0.100D-06
Relative loglikelihood change 0.100D-06
Derivative 0.100D-05
Optimization Specifications for the M step of the EM Algorithm for
Categorical Latent variables
Number of M step iterations 1
M step convergence criterion 0.100D-05
Basis for M step termination ITERATION
Optimization Specifications for the M step of the EM Algorithm for
Censored, Binary or Ordered Categorical (Ordinal), Unordered
Categorical (Nominal) and Count Outcomes
Number of M step iterations 1
M step convergence criterion 0.100D-05
Basis for M step termination ITERATION
Maximum value for logit thresholds 15
Minimum value for logit thresholds -15
Minimum expected cell size for chi-square 0.100D-01
Optimization algorithm EMA
Random Starts Specifications
Number of initial stage random starts 10
Number of final stage optimizations 2
Number of initial stage iterations 10
Initial stage convergence criterion 0.100D+01
Random starts scale 0.500D+01
Random seed for generating random starts 0
Link LOGIT
Input data file(s)
d:datamplus73recode.dat
Input data format FREE
SUMMARY OF CATEGORICAL DATA PROPORTIONS
U1
Category 1 0.678
Category 2 0.322
U2
Category 1 0.686
Category 2 0.314
RC3
Category 1 0.678
Category 2 0.322
RC4
Category 1 0.666
Category 2 0.334
RANDOM STARTS RESULTS RANKED FROM THE BEST TO THE WORST LOGLIKELIHOOD VALUES
Final stage loglikelihood values at local maxima, seeds, and initial stage start numbers:
-965.244 253358 2
-965.244 285380 1
THE MODEL ESTIMATION TERMINATED NORMALLY
TESTS OF MODEL FIT
Loglikelihood
H0 Value -965.244
H0 Scaling Correction Factor 1.013
for MLR
Information Criteria
Number of Free Parameters 9
Akaike (AIC) 1948.488
Bayesian (BIC) 1986.420
Sample-Size Adjusted BIC 1957.853
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit for the Binary and Ordered Categorical
(Ordinal) Outcomes
Pearson Chi-Square
Value 6.287
Degrees of Freedom 6
P-Value 0.3918
Likelihood Ratio Chi-Square
Value 5.605
Degrees of Freedom 6
P-Value 0.4688
FINAL CLASS COUNTS AND PROPORTIONS FOR THE LATENT CLASSES
BASED ON THE ESTIMATED MODEL
Latent
Classes
1 136.38034 0.27276
2 363.61966 0.72724
FINAL CLASS COUNTS AND PROPORTIONS FOR THE LATENT CLASS PATTERNS
BASED ON ESTIMATED POSTERIOR PROBABILITIES
Latent
Classes
1 136.38059 0.27276
2 363.61941 0.72724
CLASSIFICATION QUALITY
Entropy 0.904
CLASSIFICATION OF INDIVIDUALS BASED ON THEIR MOST LIKELY LATENT CLASS MEMBERSHIP
Class Counts and Proportions
Latent
Classes
1 127 0.25400
2 373 0.74600
Average Latent Class Probabilities for Most Likely Latent Class Membership (Row)
by Latent Class (Column)
1 2
1 0.986 0.014
2 0.030 0.970
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Latent Class 1
Thresholds
U1$1 -2.063 0.373 -5.536 0.000
U2$1 -1.724 0.300 -5.755 0.000
RC3$1 -2.331 0.390 -5.985 0.000
RC4$1 -2.078 0.320 -6.490 0.000
Latent Class 2
Thresholds
U1$1 2.091 0.182 11.502 0.000
U2$1 2.056 0.180 11.401 0.000
RC3$1 2.187 0.203 10.760 0.000
RC4$1 1.937 0.183 10.613 0.000
Categorical Latent Variables
Means
C#1 -0.981 0.116 -8.468 0.000
RESULTS IN PROBABILITY SCALE
Latent Class 1
U1
Category 1 0.113 0.037 3.024 0.002
Category 2 0.887 0.037 23.800 0.000
U2
Category 1 0.151 0.038 3.934 0.000
Category 2 0.849 0.038 22.056 0.000
RC3
Category 1 0.089 0.031 2.817 0.005
Category 2 0.911 0.031 28.987 0.000
RC4
Category 1 0.111 0.032 3.514 0.000
Category 2 0.889 0.032 28.072 0.000
Latent Class 2
U1
Category 1 0.890 0.018 50.016 0.000
Category 2 0.110 0.018 6.181 0.000
U2
Category 1 0.887 0.018 48.873 0.000
Category 2 0.113 0.018 6.256 0.000
RC3
Category 1 0.899 0.018 48.748 0.000
Category 2 0.101 0.018 5.472 0.000
RC4
Category 1 0.874 0.020 43.498 0.000
Category 2 0.126 0.020 6.267 0.000
LATENT CLASS ODDS RATIO RESULTS
Latent Class 1 Compared to Latent Class 2
U1
Category > 1 63.673 25.877 2.461 0.014
U2
Category > 1 43.796 14.941 2.931 0.003
RC3
Category > 1 91.672 38.990 2.351 0.019
RC4
Category > 1 55.439 20.032 2.768 0.006
QUALITY OF NUMERICAL RESULTS
Condition Number for the Information Matrix 0.600E-01
(ratio of smallest to largest eigenvalue)
PLOT INFORMATION
The following plots are available:
Histograms (sample values)
Scatterplots (sample values)
Sample proportions
Estimated probabilities
SAVEDATA INFORMATION
Order of variables
U1
U2
RC3
RC4
CPROB1
CPROB2
C
Save file
lca73classes.txt
Save file format Free
Save file record length 5000
To view the graphs, click on Graph and then View Graphs. From the list, we selected Estimated Probabilities.
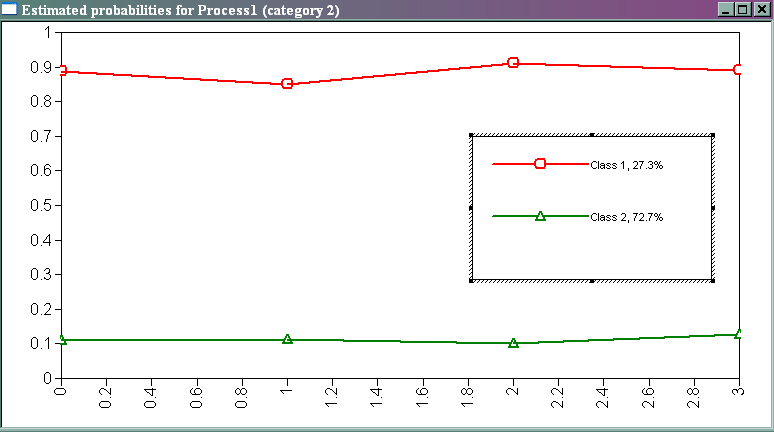
The graph above corresponds to the table in the output entitled “Results in Probability Scale”. As you can see in the title bar of the graph, the plotted points are for category 2. The y-axis is the probability, and the x-axis gives the four binary predictor variables. The variable u1 is called 0, the variable u2 is called 1, the variable rc3 is called 2, and the variable rc4 is called 3. The labeling of the x-axis starts at 0 and increases in increments of 1 because of the way we specified the series statement. We used simple syntax that did not yield a simple labeling of the x-axis.
We can see from the legend in the middle of the graph that 27.3% of this sample of students is in latent class 1, while 72.7% of the sample of students is in latent class 2. This information can be found in the table in the output entitled “Final Class Counts and Proportions for the latent Classes Based on the Estimated Model”.
The red line indicates latent class 1, which we believe is the class containing the gifted math students. Students in latent class 1 have a probability of 0.887 of having a value of 1 on the variable u1 (being in honors math in seventh grade). The green line indicates latent class 2, which we believe is the class containing the regular math students. The probability that a student in latent class 2 has value of 1 on the variable u1 is .110. The probability that a student in latent class 1 has a value of 1 on the variable u2 (being in honors math in the eighth grade) is 0.849, while the probability that a student in latent class 2 has a value of 1 on the variable u2 is only 0.113. As you can see from the graph, the students in latent class 1 have a high probability of having a value on all of the binary variables. Remember that a value of 1 on these variables indicates that the student was in honors math in that grade.
If we look at the the first few cases in the outputted file that we requested, we can see that the output and graph correspond to this file. The outputted text file does not contain variable names, but you can find this information in the output in the table entitled “Savedata Information” (towards the end of the output). This tells us that the first four variables are the observed binary variables from our mplus73recode data file, the next variable is class probability 1, then class probability 2, and the last variable (called c), is the assigned class membership. The first two students have very high probabilities for class 1 and low probabilities for class 2, and they are assigned to class 1. The last two students whose data are listed below were in no honors math classes; they have 0 probability of being in class 1, a 1.0 probability of being in class 2, and they are in class 2.
1.000 1.000 1.000 0.000 0.963 0.037 1.000
1.000 0.000 1.000 1.000 0.971 0.029 1.000
0.000 0.000 0.000 0.000 0.000 1.000 2.000
1.000 1.000 1.000 1.000 0.999 0.001 1.000
1.000 1.000 1.000 1.000 0.999 0.001 1.000
0.000 1.000 0.000 0.000 0.004 0.996 2.000
1.000 1.000 1.000 1.000 0.999 0.001 1.000
0.000 0.000 0.000 0.000 0.000 1.000 2.000
0.000 0.000 0.000 1.000 0.006 0.994 2.000
0.000 0.000 0.000 0.000 0.000 1.000 2.000
0.000 0.000 0.000 1.000 0.006 0.994 2.000
0.000 0.000 0.000 0.000 0.000 1.000 2.000
0.000 0.000 0.000 0.000 0.000 1.000 2.000
1.000 1.000 1.000 1.000 0.999 0.001 1.000
0.000 0.000 0.000 0.000 0.000 1.000 2.000
0.000 0.000 0.000 0.000 0.000 1.000 2.000
2.0 Using both categorical and continuous predictor variables
When modeling latent variables, you can use any combination of categorical and continuous variables. In this example, we will use both categorical and continuous variables.
title: Both categorical and continuous variables
data:
file is mplus73recode.dat;
variable:
names are u1-u4 rc3 rc4 x1-x10;
usevar are u1 u2 rc3 rc4 x1 - x5;
categorical are u1 u2 rc3 rc4;
classes = grp (2);
analysis:
type = mixture;
plot:
type is plot3;
series is x1-x3(*);
As you can see, the syntax is very similar to the previous example. We have five continuous variables listed on the usevariables statement (which was shorted to usevar). The name of the classes was changed to grp (you can name it anything that you want), and we again asked for plots. Please note that when you request plots, you can specify plots for either categorical or continuous variable, but not for both. Also, the types of plots available depend on the model specified. If you specify the model such that the latent classes are determined by one set of predictors and the class membership is determined by a different set of predictors, then you can get a larger variety of graphs.
Below is the abbreviated output.
*** WARNING in MODEL command
All variables are uncorrelated with all other variables within class.
Check that this is what is intended.
1 WARNING(S) FOUND IN THE INPUT INSTRUCTIONS
Both categorical and continuous variables
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 500
Number of dependent variables 9
Number of independent variables 0
Number of continuous latent variables 0
Number of categorical latent variables 1
Observed dependent variables
Continuous
X1 X2 X3 X4 X5
Binary and ordered categorical (ordinal)
U1 U2 RC3 RC4
Categorical latent variables
GRP
THE MODEL ESTIMATION TERMINATED NORMALLY
TESTS OF MODEL FIT
Loglikelihood
H0 Value -4567.250
H0 Scaling Correction Factor 0.987
for MLR
Information Criteria
Number of Free Parameters 24
Akaike (AIC) 9182.500
Bayesian (BIC) 9283.651
Sample-Size Adjusted BIC 9207.474
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit for the Binary and Ordered Categorical
(Ordinal) Outcomes
Pearson Chi-Square
Value 7.629
Degrees of Freedom 6
P-Value 0.2665
Likelihood Ratio Chi-Square
Value 6.974
Degrees of Freedom 6
P-Value 0.3233
FINAL CLASS COUNTS AND PROPORTIONS FOR THE LATENT CLASSES
BASED ON THE ESTIMATED MODEL
Latent
Classes
1 367.57723 0.73515
2 132.42277 0.26485
FINAL CLASS COUNTS AND PROPORTIONS FOR THE LATENT CLASS PATTERNS
BASED ON ESTIMATED POSTERIOR PROBABILITIES
Latent
Classes
1 367.57724 0.73515
2 132.42276 0.26485
CLASSIFICATION QUALITY
Entropy 0.998
CLASSIFICATION OF INDIVIDUALS BASED ON THEIR MOST LIKELY LATENT CLASS MEMBERSHIP
Class Counts and Proportions
Latent
Classes
1 368 0.73600
2 132 0.26400
Average Latent Class Probabilities for Most Likely Latent Class Membership (Row)
by Latent Class (Column)
1 2
1 0.999 0.001
2 0.000 1.000
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Latent Class 1
Means
X1 -2.058 0.055 -37.120 0.000
X2 -2.061 0.051 -40.653 0.000
X3 -0.987 0.055 -18.069 0.000
X4 -0.990 0.052 -19.020 0.000
X5 -0.040 0.053 -0.759 0.448
Thresholds
U1$1 2.021 0.162 12.454 0.000
U2$1 2.075 0.166 12.521 0.000
RC3$1 2.075 0.166 12.526 0.000
RC4$1 1.930 0.157 12.279 0.000
Variances
X1 1.116 0.073 15.348 0.000
X2 0.956 0.058 16.600 0.000
X3 1.031 0.059 17.382 0.000
X4 0.946 0.060 15.722 0.000
X5 1.064 0.067 15.762 0.000
Latent Class 2
Means
X1 1.988 0.091 21.874 0.000
X2 1.971 0.087 22.659 0.000
X3 0.987 0.081 12.249 0.000
X4 0.829 0.080 10.424 0.000
X5 0.097 0.095 1.022 0.307
Thresholds
U1$1 -2.102 0.283 -7.440 0.000
U2$1 -1.955 0.266 -7.353 0.000
RC3$1 -2.268 0.302 -7.516 0.000
RC4$1 -2.306 0.303 -7.617 0.000
Variances
X1 1.116 0.073 15.348 0.000
X2 0.956 0.058 16.600 0.000
X3 1.031 0.059 17.382 0.000
X4 0.946 0.060 15.722 0.000
X5 1.064 0.067 15.762 0.000
Categorical Latent Variables
Means
GRP#1 1.021 0.102 10.056 0.000
RESULTS IN PROBABILITY SCALE
Latent Class 1
U1
Category 1 0.883 0.017 52.667 0.000
Category 2 0.117 0.017 6.977 0.000
U2
Category 1 0.888 0.016 54.098 0.000
Category 2 0.112 0.016 6.792 0.000
RC3
Category 1 0.888 0.016 54.116 0.000
Category 2 0.112 0.016 6.794 0.000
RC4
Category 1 0.873 0.017 50.202 0.000
Category 2 0.127 0.017 7.284 0.000
Latent Class 2
U1
Category 1 0.109 0.027 3.972 0.000
Category 2 0.891 0.027 32.500 0.000
U2
Category 1 0.124 0.029 4.294 0.000
Category 2 0.876 0.029 30.330 0.000
RC3
Category 1 0.094 0.026 3.657 0.000
Category 2 0.906 0.026 35.325 0.000
RC4
Category 1 0.091 0.025 3.632 0.000
Category 2 0.909 0.025 36.447 0.000
LATENT CLASS ODDS RATIO RESULTS
Latent Class 1 Compared to Latent Class 2
U1
Category > 1 0.016 0.005 3.066 0.002
U2
Category > 1 0.018 0.006 3.187 0.001
RC3
Category > 1 0.013 0.004 2.906 0.004
RC4
Category > 1 0.014 0.005 2.930 0.003
References
