Mplus version 8 was used for these examples. All the files for this portion of this seminar can be downloaded here.
To illustrate longitudinal data analysis using Mplus we will use an example data set from Chapter 5 of Hox’s Multilevel Analysis: Techniques and Applications. The data set contains six GPAs for each subject measured at six time points, hence longitudinal. It has the hierarchical structure where measurements over the six time points are nested in students. Longitudinal modeling is a special case of multilevel modeling.
In Mplus a longitudinal model can be analyzed in one of the two ways: a univariate approach using the long format of the data (gpa_ch5_hox.dat) or a multivariate approach using the wide format (gpa_ch5_hox_wide.dat) of the same data. The approach using the long format is in the framework of multilevel modeling approach, while the approach using the wide format is in the framework of structural equation modeling (i.e., latent growth modeling). We will show both approaches in this section.
1.0 Longitudinal modeling in wide format, latent growth modeling
In order to perform a latent growth model, the data set will have to be restructured to wide format:
student gpa0 gpa1 gpa2 gpa3 gpa4 gpa5 job0 job1 job2 job3 job4 job5 highgpa sex 1 2.3 2.1 3 3 3 3.3 2 2 2 2 2 2 2.8 1 2 2.2 2.5 2.6 2.6 3 2.8 2 3 2 2 2 2 2.5 0 3 2.4 2.9 3 2.8 3.3 3.4 2 2 2 3 2 2 2.5 1
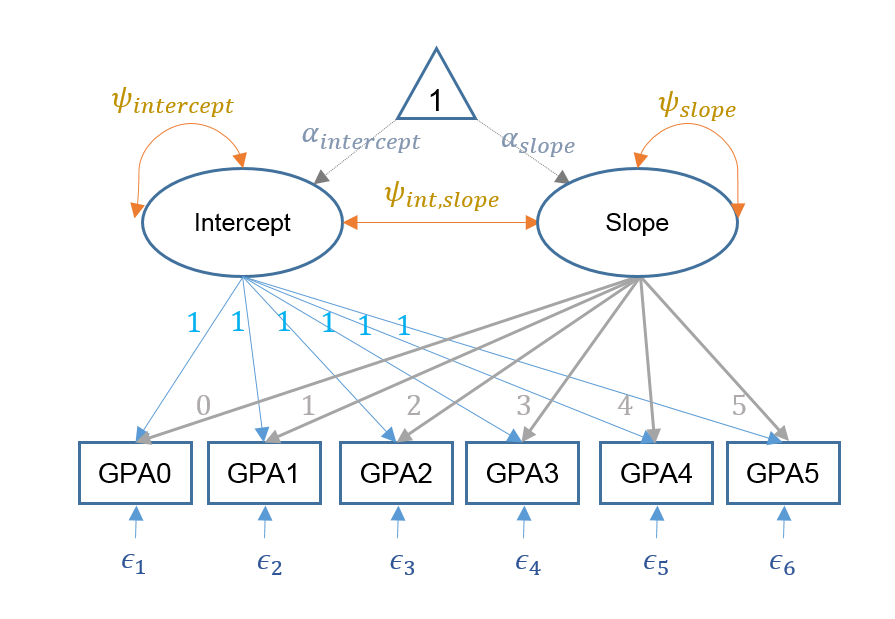
In the multivariate approach, we are more explicit about the latent variables involved in the model. In this example, we have potentially two latent variables, the random intercept and the random slope for time. We name them Intercept and Slope. We assume that the two latent are normally distributed, and we are interested in estimating the mean and variance of the two variables. The model that we are going to run is the following:
$$ GPA_i = \Lambda \eta + \epsilon_i $$
where \(\Lambda\) is a \(6 \times 2\) matrix of loadings for the intercept and slope, \(\eta\) is a \(2\times1\) vector of the latent intercept and slope with latent means \(\alpha_{intercept}\) and \(\alpha_{slope}\). The \(6 \times 1\) vector of residuals is defined by \(\epsilon\).
Here is a figure representing our latent growth model:
Multiplying out the equation above, the six equations for each time point defined for a person \(i\) and timepoint \(t\) is:
$$ GPA_{it} = Intercept_i + \lambda_t*Slope_i + e_{it} $$
for \(t={0,1,2,3,4,5}\). Equivalently, the equation above can be spelled out with the corresponding six equations:
$$\begin{eqnarray} GPA_{i0} & = & Intercept_{i} + 0*Slope_{i} + e_{i0} \\ GPA_{i1} & = & Intercept_{i} + 1*Slope_{i} + e_{i1} \\ GPA_{i2} & = & Intercept_{i} + 2*Slope_{i} + e_{i2} \\ GPA_{i3} & = & Intercept_{i} + 3*Slope_{i} + e_{i3} \\ GPA_{i4} & = & Intercept_{i} + 4*Slope_{i} + e_{i4} \\ GPA_{i5} & = & Intercept_{i} + 5*Slope_{i} + e_{i5} \end{eqnarray} $$
where the (symmetric) variance covariance matrix of the intercept and slope is defined as:
$$ \mathbf{\Psi} = \begin{bmatrix} \psi_{intercept} & \\ \psi_{int,slope} & \psi_{slope} \end{bmatrix} $$
A technical point is that in the multilevel approach, the residual variance is homogeneous across all the time points. In order to match results to the multilevel model, we will also fix the residual variance to be the same across all the six time points.
title: Wide data format with random intercept data: file is gpa_ch5_hox_wide.dat; variable: names are student admitted gpa0 gpa1 gpa2 gpa3 gpa4 gpa5 highgpa job0 job1 job2 job3 job4 job5 sex; missing are all (-9999); usevariables are gpa0 gpa1 gpa2 gpa3 gpa4 gpa5; analysis: estimator = ml; model: i s | gpa0@0 gpa1@1 gpa2@2 gpa3@3 gpa4@4 gpa5@5; gpa0 - gpa5 (1); !fix the residual variance to be same across time pointsMODEL RESULTS Two-Tailed Estimate S.E. Est./S.E. P-Value I | GPA0 1.000 0.000 999.000 999.000 GPA1 1.000 0.000 999.000 999.000 GPA2 1.000 0.000 999.000 999.000 GPA3 1.000 0.000 999.000 999.000 GPA4 1.000 0.000 999.000 999.000 GPA5 1.000 0.000 999.000 999.000 S | GPA0 0.000 0.000 999.000 999.000 GPA1 1.000 0.000 999.000 999.000 GPA2 2.000 0.000 999.000 999.000 GPA3 3.000 0.000 999.000 999.000 GPA4 4.000 0.000 999.000 999.000 GPA5 5.000 0.000 999.000 999.000 S WITH I -0.001 0.002 -0.834 0.404 Means I 2.599 0.018 141.947 0.000 S 0.106 0.006 18.111 0.000 Intercepts GPA0 0.000 0.000 999.000 999.000 GPA1 0.000 0.000 999.000 999.000 GPA2 0.000 0.000 999.000 999.000 GPA3 0.000 0.000 999.000 999.000 GPA4 0.000 0.000 999.000 999.000 GPA5 0.000 0.000 999.000 999.000 Variances I 0.045 0.007 6.599 0.000 S 0.004 0.001 6.387 0.000 Residual Variances GPA0 0.042 0.002 20.000 0.000 GPA1 0.042 0.002 20.000 0.000 GPA2 0.042 0.002 20.000 0.000 GPA3 0.042 0.002 20.000 0.000 GPA4 0.042 0.002 20.000 0.000 GPA5 0.042 0.002 20.000 0.000
2.0 Longitudinal modeling in wide format, without constraining the error variances
Now let’s rerun our previous example, but relax our assumption on residual variance. In this example, we allow the residual variance across the six time points to be different from each other. To this end, we just simply comment out last line of the code in which we constrain the residual variance to be the same. The point is that this approach in wide format gives us more flexibility in modeling besides a different angle to look at the same model.
title: Wide data format without constraining the error variances
data:
file is gpa_ch5_hox_wide.dat;
variable:
names are student admitted gpa0 gpa1 gpa2 gpa3 gpa4 gpa5
highgpa job0 job1 job2 job3 job4 job5 sex;
missing are all (-9999);
usevariables are gpa0 gpa1 gpa2 gpa3 gpa4 gpa5;
analysis:
estimator = ml;
model:
i s | gpa0@0 gpa1@1 gpa2@2 gpa3@3 gpa4@4 gpa5@5;
s@0;
!gpa0 - gpa5 (1);
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
I |
GPA0 1.000 0.000 999.000 999.000
GPA1 1.000 0.000 999.000 999.000
GPA2 1.000 0.000 999.000 999.000
GPA3 1.000 0.000 999.000 999.000
GPA4 1.000 0.000 999.000 999.000
GPA5 1.000 0.000 999.000 999.000
S |
GPA0 0.000 0.000 999.000 999.000
GPA1 1.000 0.000 999.000 999.000
GPA2 2.000 0.000 999.000 999.000
GPA3 3.000 0.000 999.000 999.000
GPA4 4.000 0.000 999.000 999.000
GPA5 5.000 0.000 999.000 999.000
S WITH
I 0.002 0.002 1.565 0.118
Means
I 2.598 0.018 141.886 0.000
S 0.106 0.005 20.317 0.000
Intercepts
GPA0 0.000 0.000 999.000 999.000
GPA1 0.000 0.000 999.000 999.000
GPA2 0.000 0.000 999.000 999.000
GPA3 0.000 0.000 999.000 999.000
GPA4 0.000 0.000 999.000 999.000
GPA5 0.000 0.000 999.000 999.000
Variances
I 0.035 0.007 4.937 0.000
S 0.003 0.001 5.593 0.000
Residual Variances
GPA0 0.080 0.010 8.049 0.000
GPA1 0.071 0.008 8.518 0.000
GPA2 0.054 0.006 9.020 0.000
GPA3 0.029 0.003 8.486 0.000
GPA4 0.015 0.003 5.589 0.000
GPA5 0.016 0.004 4.336 0.000
3.0 Longitudinal modeling in long format – random intercept model
When the data set is in long format, it contains multiple rows per subject. In this example, each student has at most six rows of data coming from the measurements over the six time points. Here are observations of some of the variables for the first three subjects from the data set.
student time gpa job sex
1 0 2.3 2 1
1 1 2.1 2 1
1 2 3 2 1
1 3 3 2 1
1 4 3 2 1
1 5 3.3 2 1
2 0 2.2 2 0
2 1 2.5 3 0
2 2 2.6 2 0
2 3 2.6 2 0
2 4 3 2 0
2 5 2.8 2 0
3 0 2.4 2 1
3 1 2.9 2 1
3 2 3 2 1
3 3 2.8 3 1
3 4 3.3 2 1
3 5 3.4 2 1
Our first multilevel model will be that GPA is a linearly related to time. The intercept is random, meaning it could change across subjects, but the slope of time is fixed, meaning the effect of time is the same across all the subjects. Mathematically, here is our first model:
$$\begin{eqnarray} L1&: & GPA_{it} & = & \beta_{0i} + \beta_{1i}*TIME_{it} + e_{it} \\ L2&: & \beta_{0i} & = & \gamma_{00} + u_{0i} \\ && \beta_{1i} & = & \gamma_{10} \end{eqnarray}$$
where \(i\) stands for individual and \(t\) stands for time.
We also need to specify the nesting structure. The key words here for describing the nesting structures are cluster, within and between. A variable is a within variable if it is time-varying, such as the job status. A variable is a between variable if it is not time-vary, such as student’s gender. We specify the type of analysis to be twolevel and random for running a longitudinal model. The model statement is very minimal since the default model is a random intercept model.
title: Long data format with random intercept
data:
file is gpa_ch5_hox.dat;
variable:
names are student highgpa gpa job admitted occas time sex;
missing are all (-9999);
usevariables are gpa time;
cluster = student;
within = time;
analysis:
type = twolevel random;
estimator = ml; !default is mlr
model:
%within%
gpa on time;
%between%
gpa;
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 1200
Number of dependent variables 1
Number of independent variables 1
Number of continuous latent variables 0
Observed dependent variables
Continuous
GPA
Observed independent variables
TIME
Variables with special functions
Cluster variable STUDENT
Within variables
TIME
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 100
Convergence criterion 0.100D-05
Maximum number of EM iterations 500
Convergence criteria for the EM algorithm
Loglikelihood change 0.100D-02
Relative loglikelihood change 0.100D-05
Derivative 0.100D-03
Minimum variance 0.100D-03
Maximum number of steepest descent iterations 20
Maximum number of iterations for H1 2000
Convergence criterion for H1 0.100D-03
Optimization algorithm EMA
Input data file(s)
gpa_ch5_hox.dat
Input data format FREE
SUMMARY OF DATA
Number of missing data patterns 1
Number of clusters 200
Average cluster size 6.000
Estimated Intraclass Correlations for the Y Variables
Intraclass
Variable Correlation
GPA 0.411
COVARIANCE COVERAGE OF DATA
Minimum covariance coverage value 0.100
PROPORTION OF DATA PRESENT
Covariance Coverage
GPA TIME
________ ________
GPA 1.000
TIME 1.000 1.000
THE MODEL ESTIMATION TERMINATED NORMALLY
MODEL FIT INFORMATION
Number of Free Parameters 4
Loglikelihood
H0 Value -196.825
H1 Value -196.825
Information Criteria
Akaike (AIC) 401.649
Bayesian (BIC) 422.009
Sample-Size Adjusted BIC 409.304
(n* = (n + 2) / 24)
Chi-Square Test of Model Fit
Value 0.000
Degrees of Freedom 0
P-Value 1.0000
RMSEA (Root Mean Square Error Of Approximation)
Estimate 0.000
CFI/TLI
CFI 1.000
TLI 1.000
Chi-Square Test of Model Fit for the Baseline Model
Value 519.807
Degrees of Freedom 1
P-Value 0.0000
SRMR (Standardized Root Mean Square Residual)
Value for Within 0.000
Value for Between 0.000
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Within Level
GPA ON
TIME 0.106 0.004 26.109 0.000
Residual Variances
GPA 0.058 0.003 22.361 0.000
Between Level
Means
GPA 2.599 0.022 120.047 0.000
Variances
GPA 0.063 0.007 8.661 0.000
QUALITY OF NUMERICAL RESULTS
Condition Number for the Information Matrix 0.126E-01
(ratio of smallest to largest eigenvalue)
DIAGRAM INFORMATION
Mplus diagrams are currently not available for multilevel analysis.
No diagram output was produced.
4.0 Longitudinal modeling in long format – random intercept and random slope model
Our second multilevel model is a much more complicated model in which we allow both a random intercept and random slope of time on top of a more involved level-1 model where we add a new level-1 predictor variable, job. The random intercept is in turn of linear function of between variable, sex and highgpa. Mathematically, here is our second model:
$$\begin{eqnarray} L1&: & GPA_{it} & = & \beta_{0i} + \beta_{1i}*TIME + \beta_{2t}*JOB + e_{it} \\ L2&: & \beta_{0i} & = & \gamma_{00} + \gamma_{01}*HIGHGPA + \gamma_{02}*SEX + u_{0i} \\ && \beta_{1i} & = & \gamma_{10} + u_{1i} \end{eqnarray}$$
Let’s look at the model statement to see what has been added. There are two lines on the within statement. The first, gpa on job, indicates that we want a random intercept and a fixed effect for job. On the next line, we request a random slope that will be predicted by time. For the between part of the model, we will use highgpa and sex as predictors. Because we have different predictor variables for the intercept and slope, we will not have any cross-level interactions. On the last line, we allow the intercept to be correlated with the slope.
title: Long data format with random intercept and random slope
data:
file is gpa_ch5_hox.dat;
variable:
names are student highgpa gpa job admitted occas time sex;
missing are all (-9999);
usevariables are gpa time job student highgpa sex;
cluster = student;
within = time job;
between = highgpa sex;
analysis:
type = twolevel random;
estimator=ml; !default is mlr
model:
%within%
gpa on job;
s | gpa on time;
%between%
gpa on highgpa sex;
gpa with s;
SUMMARY OF ANALYSIS
Number of groups 1
Number of observations 1200
Number of dependent variables 1
Number of independent variables 4
Number of continuous latent variables 1
Observed dependent variables
Continuous
GPA
Observed independent variables
TIME JOB HIGHGPA SEX
Continuous latent variables
S
Variables with special functions
Cluster variable STUDENT
Within variables
TIME JOB
Between variables
HIGHGPA SEX
Estimator ML
Information matrix OBSERVED
Maximum number of iterations 100
Convergence criterion 0.100D-05
Maximum number of EM iterations 500
Convergence criteria for the EM algorithm
Loglikelihood change 0.100D-02
Relative loglikelihood change 0.100D-05
Derivative 0.100D-03
Minimum variance 0.100D-03
Maximum number of steepest descent iterations 20
Maximum number of iterations for H1 2000
Convergence criterion for H1 0.100D-03
Optimization algorithm EMA
Input data file(s)
gpa_ch5_hox.dat
Input data format FREE
SUMMARY OF DATA
Number of missing data patterns 1
Number of clusters 200
COVARIANCE COVERAGE OF DATA
Minimum covariance coverage value 0.100
PROPORTION OF DATA PRESENT
Covariance Coverage
GPA TIME JOB HIGHGPA SEX
________ ________ ________ ________ ________
GPA 1.000
TIME 1.000 1.000
JOB 1.000 1.000 1.000
HIGHGPA 1.000 1.000 1.000 1.000
SEX 1.000 1.000 1.000 1.000 1.000
THE MODEL ESTIMATION TERMINATED NORMALLY
MODEL FIT INFORMATION
Number of Free Parameters 9
Loglikelihood
H0 Value -90.102
Information Criteria
Akaike (AIC) 198.205
Bayesian (BIC) 244.016
Sample-Size Adjusted BIC 215.428
(n* = (n + 2) / 24)
MODEL RESULTS
Two-Tailed
Estimate S.E. Est./S.E. P-Value
Within Level
GPA ON
JOB -0.120 0.018 -6.684 0.000
Residual Variances
GPA 0.042 0.002 19.894 0.000
Between Level
GPA ON
HIGHGPA 0.090 0.026 3.393 0.001
SEX 0.117 0.032 3.641 0.000
GPA WITH
S -0.003 0.002 -1.645 0.100
Means
S 0.104 0.006 18.491 0.000
Intercepts
GPA 2.527 0.093 27.195 0.000
Variances
S 0.004 0.001 6.060 0.000
Residual Variances
GPA 0.039 0.006 6.264 0.000
QUALITY OF NUMERICAL RESULTS
Condition Number for the Information Matrix 0.523E-03
(ratio of smallest to largest eigenvalue)
DIAGRAM INFORMATION
Mplus diagrams are currently not available for multilevel analysis.
No diagram output was produced.