Table 2.3 on page 27.
We are going to use two SPSS files. The level-1 file imm10.sav and the level-2 file imm10_lev2.sav. We also assume that one has already created an SSM file based on these two files. For help on how to create an SSM file based on these SPSS files, we refer to HLM manual.
This is just a level-1 OLS regression. Variable HOMEWORK is used as uncentered and it is fixed as well as the intercept.
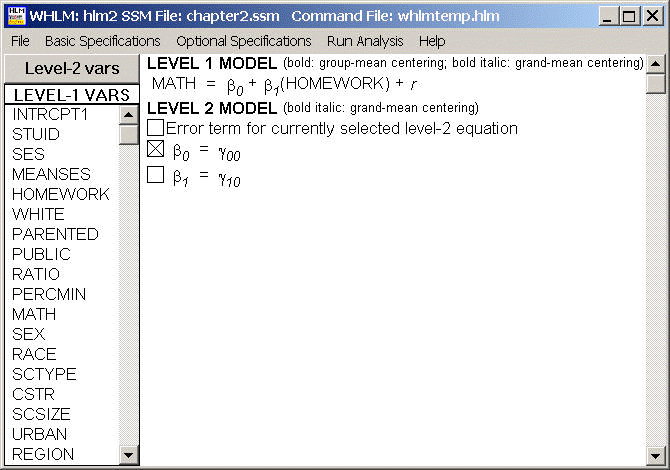
The output is as follows. Some of the output is omitted.
The outcome variable is MATH
The model specified for the fixed effects was: ----------------------------------------------------
Level-1 Level-2 Coefficients Predictors ---------------------- --------------- # INTRCPT1, B0 INTRCPT2, G00 # HOMEWORK slope, B1 INTRCPT2, G10
'#' - The residual parameter variance for this level-1 coefficient has been set
to zero.
The model specified for the covariance components was: ---------------------------------------------------------
Sigma squared (constant across level-2 units)
Summary of the model specified (in equation format) ---------------------------------------------------
Level-1 Model
Y = B0 + B1*(HOMEWORK) + R
Level-2 Model B0 = G00 B1 = G10
Least Squares Estimates -----------------------
sigma_squared = 93.73176
The outcome variable is MATH
Least-squares estimates of fixed effects
----------------------------------------------------------------------------
Standard
Fixed Effect Coefficient Error T-ratio d.f. P-value
----------------------------------------------------------------------------
For INTRCPT1, B0
INTRCPT2, G00 44.073860 0.988641 44.580 258 0.000
For HOMEWORK slope, B1
INTRCPT2, G10 3.571856 0.388237 9.200 258 0.000
----------------------------------------------------------------------------
The outcome variable is MATH
Least-squares estimates of fixed effects
(with robust standard errors)
----------------------------------------------------------------------------
Standard
Fixed Effect Coefficient Error T-ratio d.f. P-value
----------------------------------------------------------------------------
For INTRCPT1, B0
INTRCPT2, G00 44.073860 2.113577 20.853 258 0.000
For HOMEWORK slope, B1
INTRCPT2, G10 3.571856 0.728682 4.902 258 0.000
----------------------------------------------------------------------------
The robust standard errors are appropriate for datasets having a moderate to large number of level 2 units. These data do not meet this criterion.
The least-squares likelihood value = -957.799219 Deviance = 1915.59844 Number of estimated parameters = 1 The outcome variable is MATH
Least-squares estimates of fixed effects
(with robust standard errors)
----------------------------------------------------------------------------
Standard
Fixed Effect Coefficient Error T-ratio d.f. P-value
----------------------------------------------------------------------------
For INTRCPT1, B0
INTRCPT2, G00 44.073860 2.113577 20.853 258 0.000
For HOMEWORK slope, B1
INTRCPT2, G10 3.571856 0.728682 4.902 258 0.000
----------------------------------------------------------------------------
Table 2.4 on page 28.
This is a level-1 weighted OLS regression. In order to do so in HLM, we have to create a level-1 data file with aggregated data on the ten selected schools. We created this data file in SPSS and called it table2_4.sav and it looks like:
schid mmath mhwk weight 7472 45.7391 1.39130 23 7829 42.1500 2.35000 20 7930 53.2500 1.83333 24 24725 43.5455 1.63636 22 25456 49.8636 0.86364 22 25642 46.4000 1.15000 20 62821 62.8209 3.29851 67 68448 49.6667 2.09524 21 68493 46.3333 1.33333 21 72292 47.8500 1.60000 20
We need to create a new SSM file based on table2_4.sav and imm10_lev2.sav and variable weight is used as weight variable at level 1 un-normalized. One would have to say, this is a lot of work to do a level-1 regression. We could have done it easily in SPSS for that matter. The point we want to make here is that HLM has the ability to take care a weight variable.
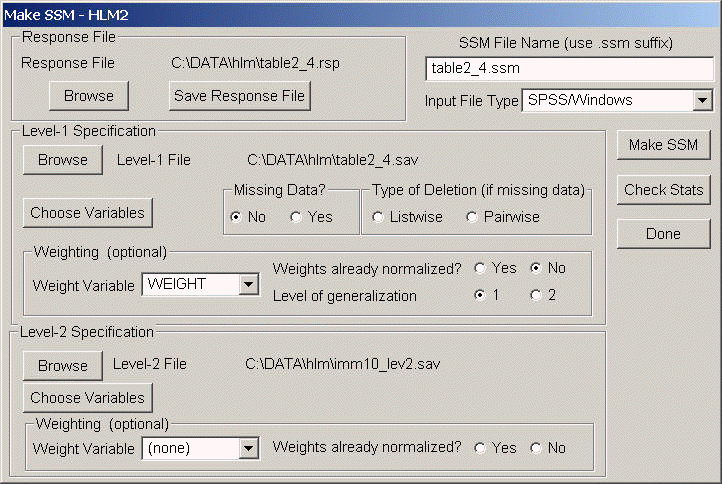
The model specification and the output is shown below. Some of the output has been omitted.
Summary of the model specified (in equation format) ---------------------------------------------------
Level-1 Model
Y = B0 + B1*(MHWK) + R
Level-2 Model B0 = G00 B1 = G10
Least Squares Estimates -----------------------
sigma_squared = 24.17109
The outcome variable is MMATH
Least-squares estimates of fixed effects
----------------------------------------------------------------------------
Standard
Fixed Effect Coefficient Error T-ratio d.f. P-value
----------------------------------------------------------------------------
For INTRCPT1, B0
INTRCPT2, G00 37.108633 4.058993 9.142 8 0.000
For MHWK slope, B1
INTRCPT2, G10 7.014745 1.853336 3.785 8 0.006
----------------------------------------------------------------------------
The outcome variable is MMATH
Least-squares estimates of fixed effects
(with robust standard errors)
----------------------------------------------------------------------------
Standard
Fixed Effect Coefficient Error T-ratio d.f. P-value
----------------------------------------------------------------------------
For INTRCPT1, B0
INTRCPT2, G00 37.108633 3.225961 11.503 8 0.000
For MHWK slope, B1
INTRCPT2, G10 7.014745 1.602668 4.377 8 0.002
----------------------------------------------------------------------------
Table 2.5 on page 29.
We go back to our original two files, imm10.sav and imm10_lev2.sav and use the same SSM file created for Table 2.3. We can simply use out old chapter2.ssm file and the only thing we have to do is to select our model. The model specified is shown in its equation format and the parameter estimates are shown below.

Summary of the model specified (in equation format) ---------------------------------------------------
Level-1 Model
Y = B0 + B1*(HOMEWORK) + R
Level-2 Model B0 = G00 + G01*(MHOMEWOR) B1 = G10
Least Squares Estimates -----------------------
sigma_squared = 82.14002
The outcome variable is MATH
Least-squares estimates of fixed effects
----------------------------------------------------------------------------
Standard
Fixed Effect Coefficient Error T-ratio d.f. P-value
----------------------------------------------------------------------------
For INTRCPT1, B0
INTRCPT2, G00 37.108633 1.467442 25.288 257 0.000
MHOMEWOR, G01 4.878110 0.797556 6.116 257 0.000
For HOMEWORK slope, B1
INTRCPT2, G10 2.136635 0.432608 4.939 257 0.000
----------------------------------------------------------------------------
Table 2.6 on page 30 using the same SSM file.
The only difference between this model and the previous one is that variable HOMEWORK is now re-entered into the model as group-mean centered. The estimates are shown below.

The model specified for the fixed effects was: ----------------------------------------------------
Level-1 Level-2
Coefficients Predictors
---------------------- ---------------
# INTRCPT1, B0 INTRCPT2, G00
MHOMEWOR, G01
* HOMEWORK slope, B1 INTRCPT2, G10
'#' - The residual parameter variance for this level-1 coefficient has been set
to zero.
'*' - This level-1 predictor has been centered around its group mean.
Summary of the model specified (in equation format) ---------------------------------------------------
Level-1 Model
Y = B0 + B1*(HOMEWORK) + R
Level-2 Model B0 = G00 + G01*(MHOMEWOR) B1 = G10 + U1
The average OLS level-1 coefficient for HOMEWORK = 1.96094
Least Squares Estimates -----------------------
sigma_squared = 82.14002
The outcome variable is MATH
Least-squares estimates of fixed effects
----------------------------------------------------------------------------
Standard
Fixed Effect Coefficient Error T-ratio d.f. P-value
----------------------------------------------------------------------------
For INTRCPT1, B0
INTRCPT2, G00 37.108633 1.467442 25.288 257 0.000
MHOMEWOR, G01 7.014744 0.670034 10.469 257 0.000
For HOMEWORK slope, B1
INTRCPT2, G10 2.136635 0.432608 4.939 257 0.000
----------------------------------------------------------------------------
