Table 6.1 on Thai educational data. This is a hierarchical generalized linear model. More precisely this is a logistic model. The setup of an SSM file is very similar to setting up an SSM file for a HLM model. We assume that an SSM file has been created and we have set up a model such as in the following screen shot.

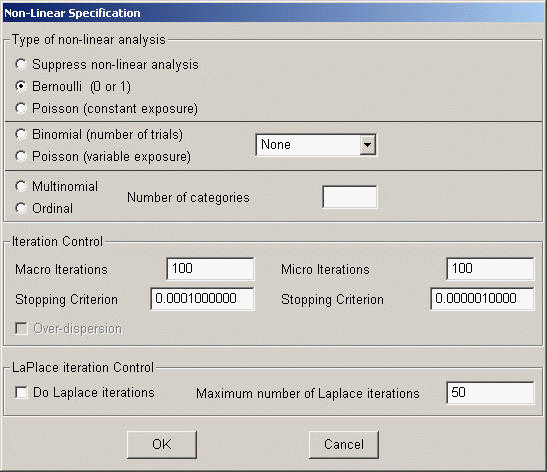
Method 1: The default estimation technique is PQL. We then set up the nonlinear part of the model. From Optional Specifications, select Setup Non-linear Model. Select Bernoulli from Type of non-linear analysis and leave other options unchanged.
From Basic Specifications, select Restricted maximal likelihood estimation method.
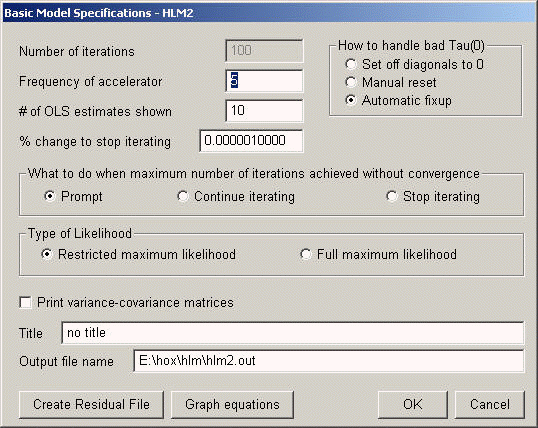
RESULTS FOR NON-LINEAR MODEL WITH THE LOGIT LINK FUNCTION: Unit-Specific Model (macro iteration 8)
Tau INTRCPT1,B0 1.34611
Tau (as correlations) INTRCPT1,B0 1.000
---------------------------------------------------- Random level-1 coefficient Reliability estimate ---------------------------------------------------- INTRCPT1, B0 0.690 ----------------------------------------------------
Final estimation of fixed effects: (Unit-specific model)
----------------------------------------------------------------------------
Standard Approx.
Fixed Effect Coefficient Error T-ratio d.f. P-value
----------------------------------------------------------------------------
For INTRCPT1, B0
INTRCPT2, G00 -2.316566 0.085600 -27.063 355 0.000
For SEX slope, B1
INTRCPT2, G10 0.513746 0.073726 6.968 7514 0.000
----------------------------------------------------------------------------
Final estimation of variance components:
-----------------------------------------------------------------------------
Random Effect Standard Variance df Chi-square P-value
Deviation Component
-----------------------------------------------------------------------------
INTRCPT1, U0 1.16022 1.34611 355 1500.02535 0.000
-----------------------------------------------------------------------------
RESULTS FOR NON-LINEAR MODEL WITH THE LOGIT LINK FUNCTION:
Population Average Model
Final estimation of fixed effects: (Population-average model)
----------------------------------------------------------------------------
Standard Approx.
Fixed Effect Coefficient Error T-ratio d.f. P-value
----------------------------------------------------------------------------
For INTRCPT1, B0
INTRCPT2, G00 -1.973530 0.079765 -24.742 355 0.000
For SEX slope, B1
INTRCPT2, G10 0.449938 0.066668 6.749 7514 0.000
----------------------------------------------------------------------------
Final estimation of fixed effects
(Population-average model with robust standard errors)
----------------------------------------------------------------------------
Standard Approx.
Fixed Effect Coefficient Error T-ratio d.f. P-value
----------------------------------------------------------------------------
For INTRCPT1, B0
INTRCPT2, G00 -1.973530 0.073613 -26.810 355 0.000
For SEX slope, B1
INTRCPT2, G10 0.449938 0.062526 7.196 7514 0.000
----------------------------------------------------------------------------
Method 2: Numerical integration technique. First of all, we select Full maximum likelihood as the type of likelihood to be estimated.
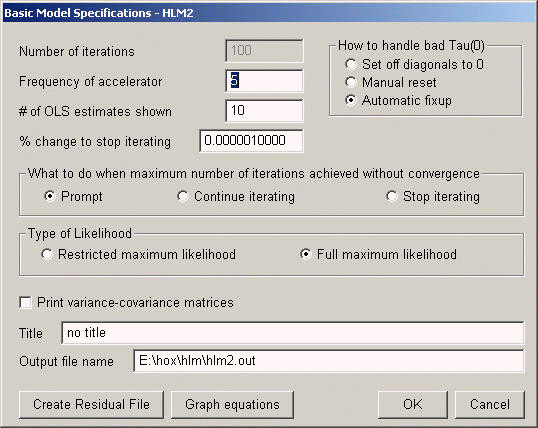
Then from the Optional Specifications-> Non-Linear Specifications, we check Laplace iteration control and set the maximum number of Laplace iterations to be 500 (rather arbitrary).
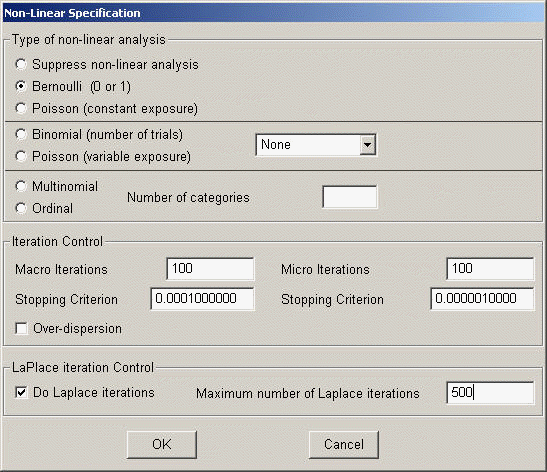
RESULTS FOR NON-LINEAR MODEL WITH THE LOGIT LINK FUNCTION: Unit-Specific Model (macro iteration 8)
Tau INTRCPT1,B0 1.33954
Standard Errors of Tau INTRCPT1,B0 0.14285
Tau (as correlations) INTRCPT1,B0 1.000
---------------------------------------------------- Random level-1 coefficient Reliability estimate ---------------------------------------------------- INTRCPT1, B0 0.689 ----------------------------------------------------
The value of the likelihood function at iteration 2 = -9.989744E+003
Final estimation of fixed effects: (Unit-specific model)
----------------------------------------------------------------------------
Standard Approx.
Fixed Effect Coefficient Error T-ratio d.f. P-value
----------------------------------------------------------------------------
For INTRCPT1, B0
INTRCPT2, G00 -2.315749 0.085475 -27.093 355 0.000
For SEX slope, B1
INTRCPT2, G10 0.513587 0.073714 6.967 7514 0.000
----------------------------------------------------------------------------
Final estimation of variance components:
-----------------------------------------------------------------------------
Random Effect Standard Variance df Chi-square P-value
Deviation Component
-----------------------------------------------------------------------------
INTRCPT1, U0 1.15738 1.33954 355 1499.52421 0.000
-----------------------------------------------------------------------------
RESULTS FOR LAPLACE-6 ITERATION 5
Tau INTRCPT1,B0 1.76868
Standard Errors of Tau INTRCPT1,B0 0.22436
Tau (as correlations) INTRCPT1,B0 1.000
---------------------------------------------------- Random level-1 coefficient Reliability estimate ---------------------------------------------------- INTRCPT1, B0 0.741 ----------------------------------------------------
Final estimation of fixed effects
(Laplace)
----------------------------------------------------------------------------
Standard Approx.
Fixed Effect Coefficient Error T-ratio d.f. P-value
----------------------------------------------------------------------------
For INTRCPT1, B0
INTRCPT2, G00 -2.531153 0.097787 -25.884 355 0.000
For SEX slope, B1
INTRCPT2, G10 0.541209 0.071905 7.527 7514 0.000
----------------------------------------------------------------------------
Statistics for current covariance components model -------------------------------------------------- Deviance = 19298.160494 Number of estimated parameters = 3 RESULTS FOR NON-LINEAR MODEL WITH THE LOGIT LINK FUNCTION: Population Average Model
Final estimation of fixed effects: (Population-average model)
----------------------------------------------------------------------------
Standard Approx.
Fixed Effect Coefficient Error T-ratio d.f. P-value
----------------------------------------------------------------------------
For INTRCPT1, B0
INTRCPT2, G00 -1.971750 0.087861 -22.442 355 0.000
For SEX slope, B1
INTRCPT2, G10 0.452572 0.068658 6.592 7514 0.000
----------------------------------------------------------------------------
Final estimation of fixed effects
(Population-average model with robust standard errors)
----------------------------------------------------------------------------
Standard Approx.
Fixed Effect Coefficient Error T-ratio d.f. P-value
----------------------------------------------------------------------------
For INTRCPT1, B0
INTRCPT2, G00 -1.971750 0.078327 -25.173 355 0.000
For SEX slope, B1
INTRCPT2, G10 0.452572 0.066032 6.854 7514 0.000
----------------------------------------------------------------------------
Table 6.2 on page 116.
