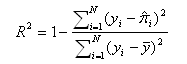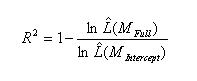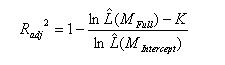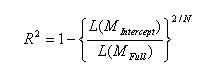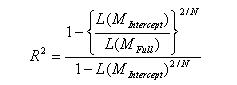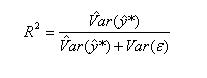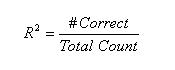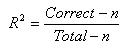FAQ: What are pseudo R-squareds?
As a starting point, recall that a non-pseudo R-squared is a statistic generated in ordinary least squares (OLS) regression that is often used as a goodness-of-fit measure. In OLS,
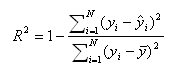
where N is the number of observations in the model, y is the dependent variable, y-bar is the mean of the y values, and y-hat is the value predicted by the model. The numerator of the ratio is the sum of the squared differences between the actual y values and the predicted y values. The denominator of the ratio is the sum of squared differences between the actual y values and their mean.
There are several approaches to thinking about R-squared in OLS. These different approaches lead to various calculations of pseudo R-squareds with regressions of categorical outcome variables.
- R-squared as explained variability – The denominator of the ratio can be thought of as the total variability in the dependent variable, or how much y varies from its mean. The numerator of the ratio can be thought of as the variability in the dependent variable that is not predicted by the model. Thus, this ratio is the proportion of the total variability unexplained by the model. Subtracting this ratio from one results in the proportion of the total variability explained by the model. The more variability explained, the better the model.
- R-squared as improvement from null model to fitted model – The denominator of the ratio can be thought of as the sum of squared errors from the null model–a model predicting the dependent variable without any independent variables. In the null model, each y value is predicted to be the mean of the y values. Consider being asked to predict a y value without having any additional information about what you are predicting. The mean of the y values would be your best guess if your aim is to minimize the squared difference between your prediction and the actual y value. The numerator of the ratio would then be the sum of squared errors of the fitted model. The ratio is indicative of the degree to which the model parameters improve upon the prediction of the null model. The smaller this ratio, the greater the improvement and the higher the R-squared.
- R-squared as the square of the correlation – The term “R-squared” is derived from this definition. R-squared is the square of the correlation between the model’s predicted values and the actual values. This correlation can range from -1 to 1, and so the square of the correlation then ranges from 0 to 1. The greater the magnitude of the correlation between the predicted values and the actual values, the greater the R-squared, regardless of whether the correlation is positive or negative.
When analyzing data with a logistic regression, an equivalent statistic to R-squared does not exist. The model estimates from a logistic regression are maximum likelihood estimates arrived at through an iterative process. They are not calculated to minimize variance, so the OLS approach to goodness-of-fit does not apply. However, to evaluate the goodness-of-fit of logistic models, several pseudo R-squareds have been developed. These are “pseudo” R-squareds because they look like R-squared in the sense that they are on a similar scale, ranging from 0 to 1 (though some pseudo R-squareds never achieve 0 or 1) with higher values indicating better model fit, but they cannot be interpreted as one would interpret an OLS R-squared and different pseudo R-squareds can arrive at very different values. Note that most software packages report the natural logarithm of the likelihood due to floating point precision problems that more commonly arise with raw likelihoods.
Commonly Encountered Pseudo R-Squareds
| Pseudo R-Squared | Formula | Description |
| Efron’s |
|
Efron’s mirrors approaches 1 and 3 from the list above–the model residuals are squared, summed, and divided by the total variability in the dependent variable, and this R-squared is also equal to the squared correlation between the predicted values and actual values. When considering Efron’s, remember that model residuals from a logistic regression are not comparable to those in OLS. The dependent variable in a logistic regression is not continuous and the predicted value (a probability) is. In OLS, the predicted values and the actual values are both continuous and on the same scale, so their differences are easily interpreted. |
| McFadden’s |
Mfull = Model with predictors Mintercept = Model without predictors |
McFadden’s mirrors approaches 1 and 2 from the list
above. The log likelihood of the intercept model is treated
as a total sum of squares, and the log likelihood of the full model is
treated as the sum of squared errors (like in approach 1).The ratio of the likelihoods suggests the level of improvement
over the intercept model offered by the full model (like in approach 2).A likelihood falls between 0 and 1, so the log of a likelihood is
less than or equal to zero. If a model has a very low likelihood,
then the log of the likelihood will have a larger magnitude than the log
of a more likely model. Thus, a small ratio of log likelihoods
indicates that the full model is a far better fit than the intercept
model.
If comparing two models on the same data, McFadden’s would be higher for the model with the greater likelihood. |
| McFadden’s (adjusted) |
|
McFadden’s adjusted mirrors the adjusted R-squared in OLS by penalizing a model for including too many predictors.If the predictors in the model are effective, then the penalty will be small relative to the added information of the predictors. However, if a model contains predictors that do not add sufficiently to the model, then the penalty becomes noticeable and the adjusted R-squared can decrease with the addition of a predictor, even if the R-squared increases slightly.Note that negative McFadden’s adjusted R-squared are possible. |
| Cox & Snell |
|
Cox & Snell’s mirrors approach 2 from the list above. The ratio of the likelihoods reflects the improvement of the full model over the intercept model (the smaller the ratio, the greater the improvement).Consider the definition of L(M). L(M) is the conditional probability of the dependent variable given the independent variables. If there are N observations in the dataset, then L(M) is the product of N such probabilities. Thus, taking the nth root of the product L(M) provides an estimate of the likelihood of each Y value. Cox & Snell’s presents the R-squared as a transformation of the –2ln[L(MIntercept)/L(MFull)] statistic that is used to determine the convergence of a logistic regression.Note that Cox & Snell’s pseudo R-squared has a maximum value that is not 1: if the full model predicts the outcome perfectly and has a likelihood of 1, Cox & Snell’s is then 1-L(MIntercept)2/N, which is less than one. |
| Nagelkerke / Cragg & Uhler’s |
|
Nagelkerke/Cragg & Uhler’s mirrors approach 2 from the list above. It adjusts Cox & Snell’s so that the range of possible values extends to 1.To achieve this, the Cox & Snell R-squared is divided by its maximum possible value, 1-L(MIntercept)2/N. Then, if the full model perfectly predicts the outcome and has a likelihood of 1, Nagelkerke/Cragg & Uhler’s R-squared = 1.When L(Mfull) = 1, then R2 = 1; When L(Mfull) = L(Mintercept), then R2 = 0. |
|
McKelvey & Zavoina
|
|
McKelvey & Zavoina’s mirrors approach 1 from the list above, but its calculations are based on predicting a continuous latent variable underlying the observed 0-1 outcomes in the data. The model predictions of the latent variable can be calculated using the model coefficients (NOT the log-odds) and the predictor variables.McKelvey & Zavoina’s also mirrors approach 3. Because of the parallel structure between McKelvey & Zavoina’s and OLS R-squareds, we can examine the square root of McKelvey & Zavoina’s to arrive at the correlation between the latent continuous variable and the predicted probabilities.Note that, because y* is not observed, we cannot calculate the variance of the error (the second term in the denominator). It is assumed to be π2/3 in logistic models. |
| Count |
|
Count R-Squared does not approach goodness of fit in a way comparable to any OLS approach. It transforms the continuous predicted probabilities into a binary variable on the same scale as the outcome variable (0-1) and then assesses the predictions as correct or incorrect.Count R-Square treats any record with a predicted probability of .5 or greater as having a predicted outcome of 1 and any record with a predicted probability less than .5 as having a predicted outcome of 0. Then, the predicted 1s that match actual 1s and predicted 0s that match actual 0s are tallied. This is the number of records correctly predicted, given this cutoff point of .5. The R-square is this correct count divided by the total count. |
| Adjusted Count |
n = Count of most frequent outcome |
The Adjusted Count R-Square mirrors approach 2 from the list above. This adjustment is unrelated to the number of predictors and is not comparable to the adjustment to OLS or McFadden’s R-Squareds.Consider this scenario: If you are asked to predict who in a list of 100 random people is left-handed or right-handed, you could guess that everyone in the list is right handed and you would be correct for the majority of the list. Your guess could be thought of as a null model.The Adjusted Count R-Squared controls for such a null model. Without knowing anything about the predictors, one could always predict the more common outcome and be right the majority of the time. An effective model should improve on this null model, and so this null model is the baseline for which the Count R-Square is adjusted. The Adjusted Count R-squared then measures the proportion of correct predictions beyond this baseline. |
A Quick Example
A logistic regression was run on 200 observations in Stata. For more on the data and the model, see Annotated Output for Logistic Regression in Stata. After running the model, entering the command fitstat gives multiple goodness-of-fit measures. You can download fitstat from within Stata by typing search spost9_ado (see How can I used the search command to search for programs and get additional help? for more information about using search).
use https://stats.idre.ucla.edu/stat/stata/notes/hsb2, clear generate honcomp = (write >=60) logit honcomp female read science
fitstat, sav(r2_1)
Measures of Fit for logit of honcomp
Log-Lik Intercept Only: -115.644 Log-Lik Full Model: -80.118
D(196): 160.236 LR(3): 71.052
Prob > LR: 0.000
McFadden's R2: 0.307 McFadden's Adj R2: 0.273
ML (Cox-Snell) R2: 0.299 Cragg-Uhler(Nagelkerke) R2: 0.436
McKelvey & Zavoina's R2: 0.519 Efron's R2: 0.330
Variance of y*: 6.840 Variance of error: 3.290
Count R2: 0.810 Adj Count R2: 0.283
AIC: 0.841 AIC*n: 168.236
BIC: -878.234 BIC': -55.158
BIC used by Stata: 181.430 AIC used by Stata: 168.236
This provides multiple pseudo R-squareds (and the information needed to calculate several more). Note that the pseudo R-squareds vary greatly from each other within the same model. Of the non-count methods, the statistics range from 0.273 (McFadden’s adjusted) to 0.519 (McKelvey & Zavoina’s).
The interpretation of an OLS R-squared is relatively straightforward: “the proportion of the total variability of the outcome that is accounted for by the model”. In building a model, the aim is usually to predict variability. The outcome variable has a range of values, and you are interested in knowing what circumstances correspond to what parts of the range. If you are looking at home values, looking at a list of home prices will give you a sense of the range of home prices. You may build a model that includes variables like location and square feet to explain the range of prices. If the R-squared value from such a model is .72, then the variables in your model predicted 72% of the variability in the prices. So most of the variability has been accounted for, but if you would like to improve your model, you might consider adding variables. You could similarly build a model that predicts test scores for students in a class using hours of study and previous test grade as predictors. If your R-squared value from this model is .75, then your model predicted 75% of the variability in the scores. Though you have predicted two different outcome variables in two different datasets using two different sets of predictors, you can compare these models using their R-squared values: the two models were able to predict similar proportions of variability in their respective outcomes, but the test scores model predicted a slightly higher proportion of the outcome variability than the home prices model. Such a comparison is not possible using pseudo R-squareds.
What characteristics of pseudo R-squareds make broad comparisons of pseudo R-squareds invalid?
Scale – OLS R-squared ranges from 0 to 1, which makes sense both because it is a proportion and because it is a squared correlation. Most pseudo R-squareds do not range from 0 to1. For an example of a pseudo R-squared that does not range from 0-1, consider Cox & Snell’s pseudo R-squared. As pointed out in the table above, if a full model predicts an outcome perfectly and has a likelihood of 1, Cox & Snell’s pseudo R-squared is then 1-L(MIntercept)2/N, which is less than one. If two logistic models, each with N observations, predict different outcomes and both predict their respective outcomes perfectly, then the Cox & Snell pseudo R-squared for the two models is (1-L(MIntercept)2/N). However, this value is not the same for the two models. The models predicted their outcomes equally well, but this pseudo R-squared will be higher for one model than the other, suggesting a better fit. Thus, these pseudo R-squareds cannot be compared in this way.
Some pseudo R-squareds do range from 0-1, but only superficially to more closely match the scale of the OLS R-squared. For example, Nagelkerke/Cragg & Uhler’s pseudo R-squared is an adjusted Cox & Snell that rescales by a factor of 1/( 1-L(MIntercept)2/N). This too presents problems when comparing across models. Consider two logistic models, each with N observations, predicting different outcomes and failing to improve upon the intercept model. That is, L(MFull)/L(MIntercept)=1 for both models. Arguably, these models predicted their respective outcomes equally poorly. However, the two models will have different Nagelkerke/Cragg & Uhler’s pseudo R-squareds. Thus, these pseudo R-squareds cannot be compared in this way.
Intention – Recall that OLS minimizes the squared differences between the predictions and the actual values of the predicted variable. This is not true for logistic regression. The way in which R-squared is calculated in OLS regression captures how well the model is doing what it aims to do. Different methods of the pseudo R-squared reflect different interpretations of the aims of the model. In evaluating a model, this is something to keep in mind. For example, Efron’s R-squared and the Count R-squared evaluate models according to very different criteria: both examine the residuals–the difference between the outcome values and predicted probabilities–but they treat the residuals very differently. Efron’s sums the squared residuals and assesses the model based on this sum. Two observations with small a differences in their residuals (say, 0.49 vs. 0.51) will have small differences in their squared residuals and these predictions are considered similar by Efron’s. The Count R-squared, on the other hand, assesses the model based solely on what proportion of the residuals are less than .5. Thus, the two observations with residuals 0.49 and 0.51 are considered very differently: the observation with the residual of 0.49 is considered a “correct” prediction while the observation with the residual of 0.51 is considered an “incorrect” prediction. When comparing two logistic models predicting different outcomes, the intention of the models may not be captured by a single pseudo R-squared, and comparing the models with a single pseudo R-squared may be deceptive.
For some context, we can examine another model predicting the same variable in the same dataset as the model above, but with one added variable. Stata allows us to compare the fit statistics of this new model and the previous model side-by-side.
logit honcomp female read science math
fitstat, using(r2_1)
Measures of Fit for logit of honcomp
Current Saved Difference
Model: logit logit
N: 200 200 0
Log-Lik Intercept Only -115.644 -115.644 0.000
Log-Lik Full Model -73.643 -80.118 6.475
D 147.286(195) 160.236(196) 12.951(1)
LR 84.003(4) 71.052(3) 12.951(1)
Prob > LR 0.000 0.000 0.000
McFadden's R2 0.363 0.307 0.056
McFadden's Adj R2 0.320 0.273 0.047
ML (Cox-Snell) R2 0.343 0.299 0.044
Cragg-Uhler(Nagelkerke) R2 0.500 0.436 0.064
McKelvey & Zavoina's R2 0.560 0.519 0.041
Efron's R2 0.388 0.330 0.058
Variance of y* 7.485 6.840 0.645
Variance of error 3.290 3.290 0.000
Count R2 0.840 0.810 0.030
Adj Count R2 0.396 0.283 0.113
AIC 0.786 0.841 -0.055
AIC*n 157.286 168.236 -10.951
BIC -885.886 -878.234 -7.652
BIC' -62.810 -55.158 -7.652
BIC used by Stata 173.777 181.430 -7.652
AIC used by Stata 157.286 168.236 -10.951
All of the pseudo R-squareds reported here agree that this model better fits the outcome data than the previous model. While pseudo R-squareds cannot be interpreted independently or compared across datasets, they are valid and useful in evaluating multiple models predicting the same outcome on the same dataset. In other words, a pseudo R-squared statistic without context has little meaning. A pseudo R-squared only has meaning when compared to another pseudo R-squared of the same type, on the same data, predicting the same outcome. In this situation, the higher pseudo R-squared indicates which model better predicts the outcome.
Attempts have been made to asses the accuracy of various pseudo R-squareds by predicting a continuous latent variable through OLS regression and its observed binary variable through logistic regression and comparing the pseudo R-squareds to the OLS R-squared. In such simulations, McKelvey & Zavoina’s was the closest to the OLS R-squared.
References
Freese, Jeremy and J. Scott Long. Regression Models for Categorical Dependent Variables Using Stata. College Station: Stata Press, 2006.
Long, J. Scott. Regression Models for Categorical and Limited Dependent Variables. Thousand Oaks: Sage Publications, 1997.
Updated: October 20, 2011