Consider the six graphs of the nonlinear (curvilinear) relationships depicted below.
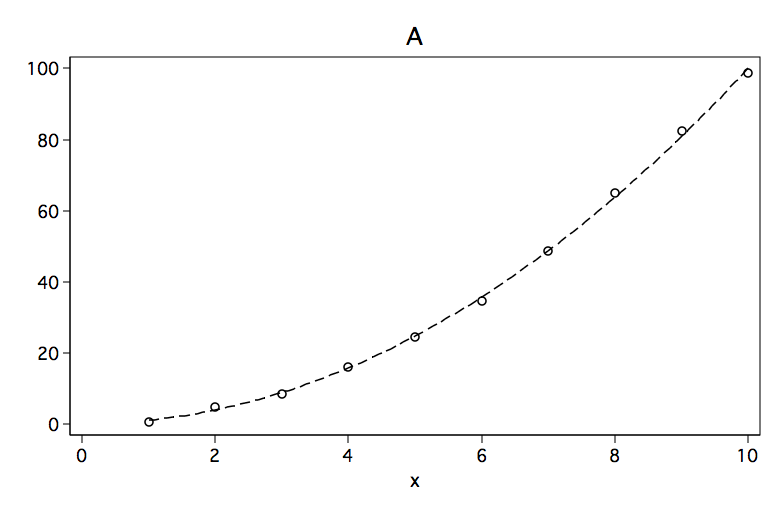
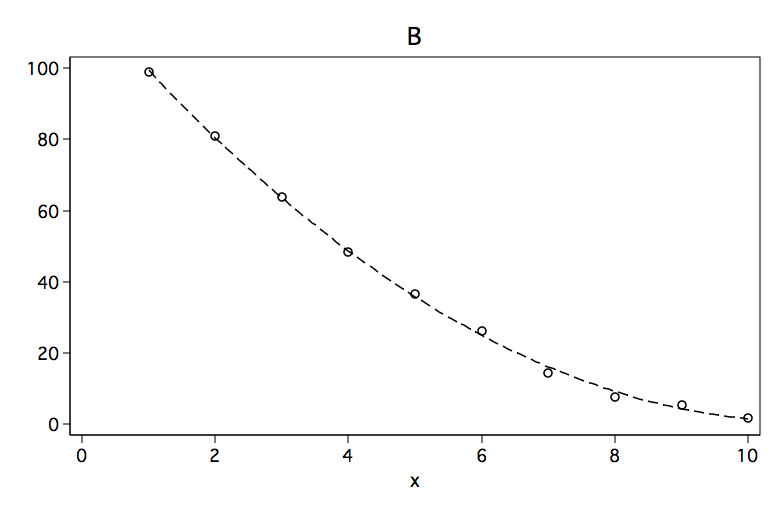
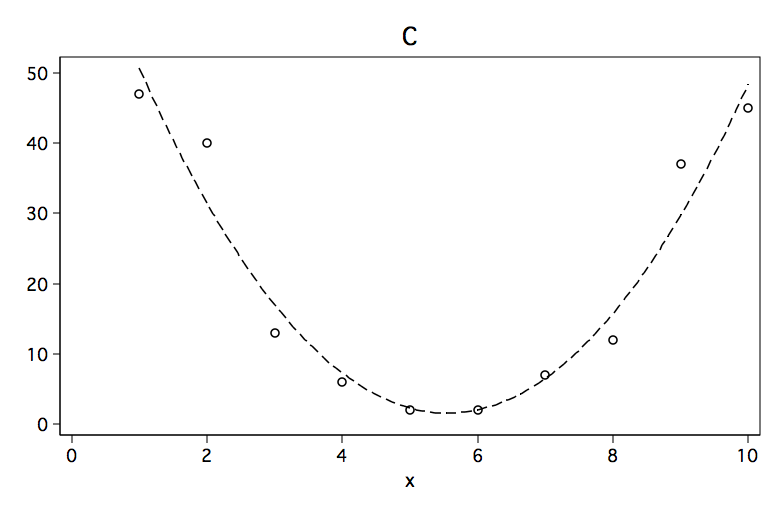
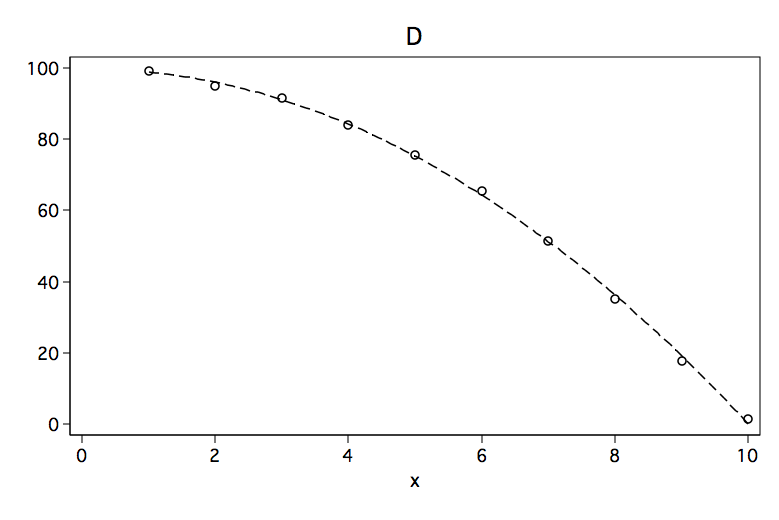
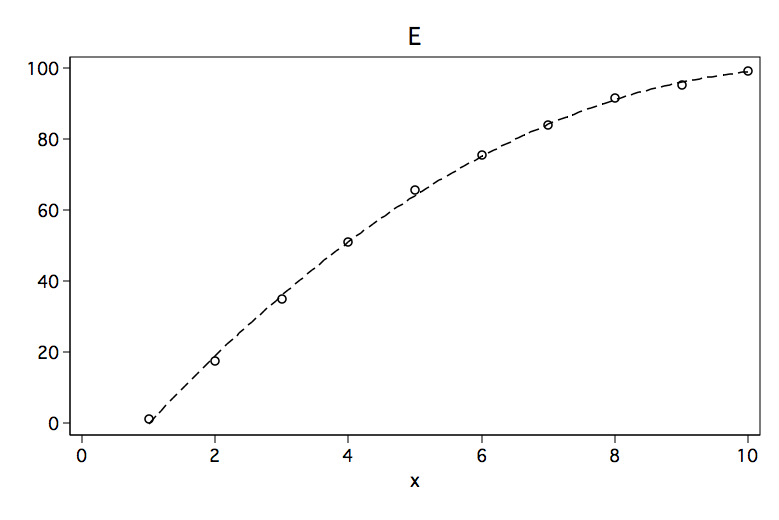
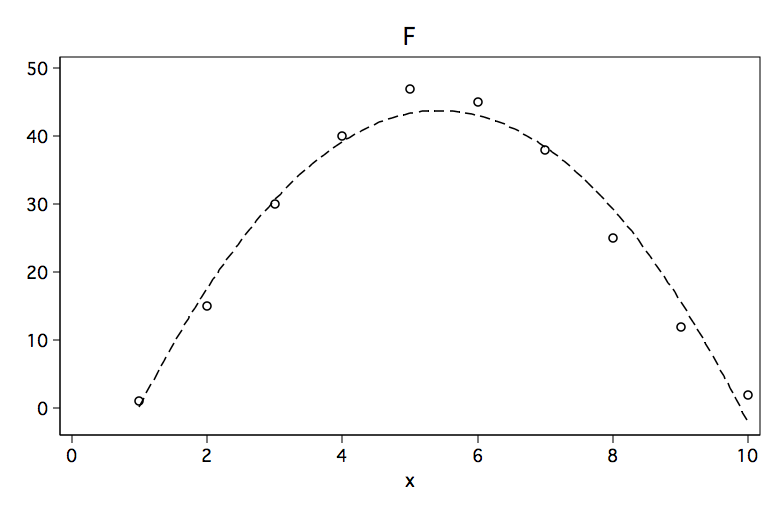
Although each of the six figures look like very different curves, there are some similarities. For example, curves A, B and C would be considered to be convex (apex at the bottom, curve opens up) while curves D, E and F are concave (apex at the top, curve opens down).
Below are the results of fitting a polynomial regression model to data points for each of the six figures. The predictors in the model are x and x2 where x2 is x^2. Please note the sign for x2 in each of the models. The sign is positive when the model is convex and negative when the curve is concave.
------------------------------------------------------------------------------
Model A | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | -.1839751 .5230228 -0.35 0.735 -1.420728 1.052777
x2 | 1.016747 .0463379 21.94 0.000 .9071754 1.126319
constant | .2076584 1.252323 0.17 0.873 -2.753615 3.168931
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Model B | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | -21.93563 .550781 -39.83 0.000 -23.23802 -20.63324
x2 | 1.003714 .0487971 20.57 0.000 .8883275 1.119101
constant | 120.3872 1.318787 91.29 0.000 117.2688 123.5057
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Model C | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | -26.33182 2.511897 -10.48 0.000 -32.27151 -20.39213
x2 | 2.371212 .2225446 10.65 0.000 1.844978 2.897447
constant | 74.63333 6.014471 12.41 0.000 60.41137 88.8553
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Model D | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | .1839751 .5230227 0.35 0.735 -1.052777 1.420727
x2 | -1.016747 .0463378 -21.94 0.000 -1.126319 -.9071754
constant | 99.79234 1.252322 79.69 0.000 96.83107 102.7536
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Model E | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | 22.15 .5390466 41.09 0.000 20.87536 23.42464
x2 | -1.012121 .0477575 -21.19 0.000 -1.12505 -.8991926
constant | -21.27333 1.29069 -16.48 0.000 -24.32533 -18.22133
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Model F | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x | 24.10227 1.615884 14.92 0.000 20.28132 27.92323
x2 | -2.215909 .1431612 -15.48 0.000 -2.554432 -1.877387
constant | -21.75 3.869062 -5.62 0.001 -30.89888 -12.60112
------------------------------------------------------------------------------
Okay, so the quadratic term, x2, indicates which way the curve is bending but what’s up with the linear term, x, it doesn’t seem to make sense. The explanation for this will require a bit of math but the solution is actually rather easy. Let’s look at the linear model.
- y = b0 + b1*x + b2*x2
If we differentiate with respect to x we get,
- y’ = b1 + 2*b2*x.
What this shows is that b1 gives the rate of change when x is equal to zero. In our example above x = 0 is not within range of our observed values. The coefficient b2 tells both the direction and steepness of the curvature (a positive value indicates the curvature is upwards while a negative value indicates the curvature is downwards).
So the trick is to place the zero value within the range of our data. We will do this by centering the x, that is, we will subtract the mean of x from each value. We will call this new variable c and we will then create c2 by squaring c. Next, we will rerun the four regression models. You note that the coefficient for the quadratic term are unchanged while the coefficient for the linear better reflect the linear relation, which in the case of Models C and F should be somewhat near zero.
------------------------------------------------------------------------------
Model A | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
c | 11.00024 .1172265 93.84 0.000 10.72304 11.27744
c2 | 1.016747 .0463379 21.94 0.000 .9071754 1.126319
constant | 29.95239 .5094267 58.80 0.000 28.74779 31.15699
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Model B | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
c | -10.89477 .123448 -88.25 0.000 -11.18668 -10.60286
c2 | 1.003714 .0487971 20.57 0.000 .8883275 1.119101
constant | 30.10364 .5364633 56.12 0.000 28.83511 31.37218
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Model C | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
c | -.2484848 .5629983 -0.44 0.672 -1.579764 1.082795
c2 | 2.371212 .2225446 10.65 0.000 1.844978 2.897447
constant | 1.5375 2.446599 0.63 0.550 -4.247788 7.322788
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Model D | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
c | -11.00024 .1172265 -93.84 0.000 -11.27744 -10.72304
c2 | -1.016747 .0463378 -21.94 0.000 -1.126319 -.9071754
constant | 70.04761 .5094266 137.50 0.000 68.84301 71.25221
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Model E | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
c | 11.01667 .120818 91.18 0.000 10.73098 11.30236
c2 | -1.012121 .0477575 -21.19 0.000 -1.12505 -.8991926
constant | 69.935 .525034 133.20 0.000 68.69349 71.17651
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Model F | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
c | -.2727273 .3621724 -0.75 0.476 -1.129129 .5836743
c2 | -2.215909 .1431612 -15.48 0.000 -2.554432 -1.877387
constant | 43.78125 1.573878 27.82 0.000 40.05962 47.50288
------------------------------------------------------------------------------
As an added benefit centering the x variable reduces the correlation between the linear and quadratic terms. The correlation between x and x2 is 0.975 while the correlation between c and c2 is 0.000.
