This page briefly introduces linear mixed models LMMs as a method for analyzing data that are non independent, multilevel/hierarchical, longitudinal, or correlated. We focus on the general concepts and interpretation of LMMS, with less time spent on the theory and technical details.
Background
Linear mixed models are an extension of simple linear models to allow both fixed and random effects, and are particularly used when there is non independence in the data, such as arises from a hierarchical structure. For example, students could be sampled from within classrooms, or patients from within doctors.
When there are multiple levels, such as patients seen by the same doctor, the variability in the outcome can be thought of as being either within group or between group. Patient level observations are not independent, as within a given doctor patients are more similar. Units sampled at the highest level (in our example, doctors) are independent. The figure below shows a sample where the dots are patients within doctors, the larger circles.
There are multiple ways to deal with hierarchical data. One simple approach is to aggregate. For example, suppose 10 patients are sampled from each doctor. Rather than using the individual patients’ data, which is not independent, we could take the average of all patients within a doctor. This aggregated data would then be independent.
Although aggregate data analysis yields consistent effect estimates and standard errors, it does not really take advantage of all the data, because patient data are simply averaged. Looking at the figure above, at the aggregate level, there would only be six data points.
Another approach to hierarchical data is analyzing data from one unit at a time. Again in our example, we could run six separate linear regressions—one for each doctor in the sample. Again although this does work, there are many models, and each one does not take advantage of the information in data from other doctors. This can also make the results “noisy” in that the estimates from each model are not based on very much data
Linear mixed models (also called multilevel models) can be thought of as a trade off between these two alternatives. The individual regressions has many estimates and lots of data, but is noisy. The aggregate is less noisy, but may lose important differences by averaging all samples within each doctor. LMMs are somewhere inbetween.
Beyond just caring about getting standard errors corrected for non independence in the data, there can be important reasons to explore the difference between effects within and between groups. An example of this is shown in the figure below. Here we have patients from the six doctors again, and are looking at a scatter plot of the relation between a predictor and outcome. Within each doctor, the relation between predictor and outcome is negative. However, between doctors, the relation is positive. LMMs allow us to explore and understand these important effects.
Random Effects
The core of mixed models is that they incorporate fixed and random effects. A fixed effect is a parameter that does not vary. For example, we may assume there is some true regression line in the population, \(\beta\), and we get some estimate of it, \(\hat{\beta}\). In contrast, random effects are parameters that are themselves random variables. For example, we could say that \(\beta\) is distributed as a random normal variate with mean \(\mu\) and standard deviation \(\sigma\), or in equation form:
$$ \beta \sim \mathcal{N}(\mu, \sigma) $$
This is really the same as in linear regression, where we assume the data are random variables, but the parameters are fixed effects. Now the data are random variables, and the parameters are random variables (at one level), but fixed at the highest level (for example, we still assume some overall population mean, \(\mu\) ).
Theory of Linear Mixed Models
$$ \mathbf{y} = \boldsymbol{X\beta} + \boldsymbol{Zu} + \boldsymbol{\varepsilon} $$
Where \(\mathbf{y}\) is a \(N \times 1\) column vector, the outcome variable; \(\mathbf{X}\) is a \(N \times p\) matrix of the \(p\) predictor variables; \(\boldsymbol{\beta}\) is a \(p \times 1\) column vector of the fixed-effects regression coefficients (the \(\beta\)s); \(\mathbf{Z}\) is the \(N \times qJ\) design matrix for the \(q\) random effects and \(J\) groups; \(\boldsymbol{u}\) is a \(qJ \times 1\) vector of \(q\) random effects (the random complement to the fixed \(\boldsymbol{\beta})\) for \(J\) groups; and \(\boldsymbol{\varepsilon}\) is a \(N \times 1\) column vector of the residuals, that part of \(\mathbf{y}\) that is not explained by the model, \(\boldsymbol{X\beta} + \boldsymbol{Zu}\). To recap:
$$ \overbrace{\mathbf{y}}^{\mbox{N x 1}} \quad = \quad \overbrace{\underbrace{\mathbf{X}}_{\mbox{N x p}} \quad \underbrace{\boldsymbol{\beta}}_{\mbox{p x 1}}}^{\mbox{N x 1}} \quad + \quad \overbrace{\underbrace{\mathbf{Z}}_{\mbox{N x qJ}} \quad \underbrace{\boldsymbol{u}}_{\mbox{qJ x 1}}}^{\mbox{N x 1}} \quad + \quad \overbrace{\boldsymbol{\varepsilon}}^{\mbox{N x 1}} $$
To make this more concrete, let’s consider an example from a simulated dataset. Doctors (\(J = 407\)) indexed by the \(j\) subscript each see \(n_{j}\) patients. So our grouping variable is the doctor. Not every doctor sees the same number of patients, ranging from just 2 patients all the way to 40 patients, averaging about 21. The total number of patients is the sum of the patients seen by each doctor
$$ N = \sum_{j}^J n_j $$
In our example, \(N = 8525\) patients were seen by doctors. Our outcome, \(\mathbf{y}\) is a continuous variable, mobility scores. Further, suppose we had 6 fixed effects predictors, Age (in years), Married (0 = no, 1 = yes), Sex (0 = female, 1 = male), Red Blood Cell (RBC) count, and White Blood Cell (WBC) count plus a fixed intercept and one random intercept ($q=1$) for each of the $J=407$ doctors. For simplicity, we are only going to consider random intercepts. We will let every other effect be fixed for now. The reason we want any random effects is because we expect that mobility scores within doctors may be correlated. There are many reasons why this could be. For example, doctors may have specialties that mean they tend to see lung cancer patients with particular symptoms or some doctors may see more advanced cases, such that within a doctor, patients are more homogeneous than they are between doctors. To put this example back in our matrix notation, for the \(n_{j}\) dimensional response \(\mathbf{y_j}\) for doctor \(j\) we would have:
$$ \overbrace{\mathbf{y_j}}^{n_j \times 1} \quad = \quad \overbrace{\underbrace{\mathbf{X_j}}_{n_j \times 6} \quad \underbrace{\boldsymbol{\beta}}_{6 \times 1}}^{n_j \times 1} \quad + \quad \overbrace{\underbrace{\mathbf{Z_j}}_{n_j \times 1} \quad \underbrace{u_j}_{1 \times 1}}^{n_j \times 1} \quad + \quad \overbrace{\boldsymbol{\varepsilon_j}}^{n_j \times 1} $$
and by stacking observations from all groups together, since $q=1$ for the random intercept model, $qJ=(1)(407)=407$ so we have:
$$ \overbrace{\mathbf{y}}^{ 8525 \times 1} \quad = \quad \overbrace{\underbrace{\mathbf{X}}_{ 8525 \times 6} \quad \underbrace{\boldsymbol{\beta}}_{6 \times 1}}^{ 8525 \times 1} \quad + \quad \overbrace{\underbrace{\mathbf{Z}}_{ 8525 \times 407} \quad \underbrace{\boldsymbol{u}}_{ 407 \times 1}}^{ 8525 \times 1} \quad + \quad \overbrace{\boldsymbol{\varepsilon}}^{ 8525 \times 1} $$
$$ \mathbf{y} = \left[ \begin{array}{l} \text{mobility} \\ 2 \\ 2 \\ \ldots \\ 3 \end{array} \right] \begin{array}{l} n_{ij} \\ 1 \\ 2 \\ \ldots \\ 8525 \end{array} \quad \mathbf{X} = \left[ \begin{array}{llllll} \text{Intercept} & \text{Age} & \text{Married} & \text{Sex} & \text{WBC} & \text{RBC} \\ 1 & 64.97 & 0 & 1 & 6087 & 4.87 \\ 1 & 53.92 & 0 & 0 & 6700 & 4.68 \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ 1 & 56.07 & 0 & 1 & 6430 & 4.73 \\ \end{array} \right] $$
$$ \boldsymbol{\beta} = \left[ \begin{array}{c} 4.782 \\ .025 \\ .011 \\ .012 \\ 0 \\ -.009 \end{array} \right] $$
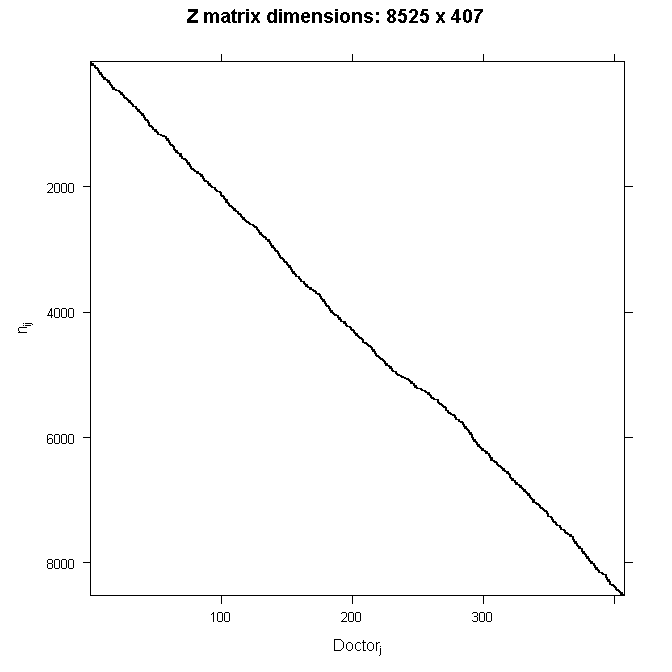
Because \(\mathbf{Z}\) is so big, we will not write out the numbers here. Because we are only modeling random intercepts, it is a special matrix in our case that only codes which doctor a patient belongs to. So in this case, it is all 0s and 1s. Each column is one doctor and each row represents one patient (one row in the dataset). If the patient belongs to the doctor in that column, the cell will have a 1, 0 otherwise. This also means that it is a sparse matrix (i.e., a matrix of mostly zeros) and we can create a picture representation easily. Note that if we added a random slope, the number of rows in \(\mathbf{Z}\) would remain the same, but the number of columns would double. This is why it can become computationally burdensome to add random effects, particularly when you have a lot of groups (we have 407 doctors). In all cases, the matrix will contain mostly zeros, so it is always sparse. In the graphical representation, the line appears to wiggle because the number of patients per doctor varies.
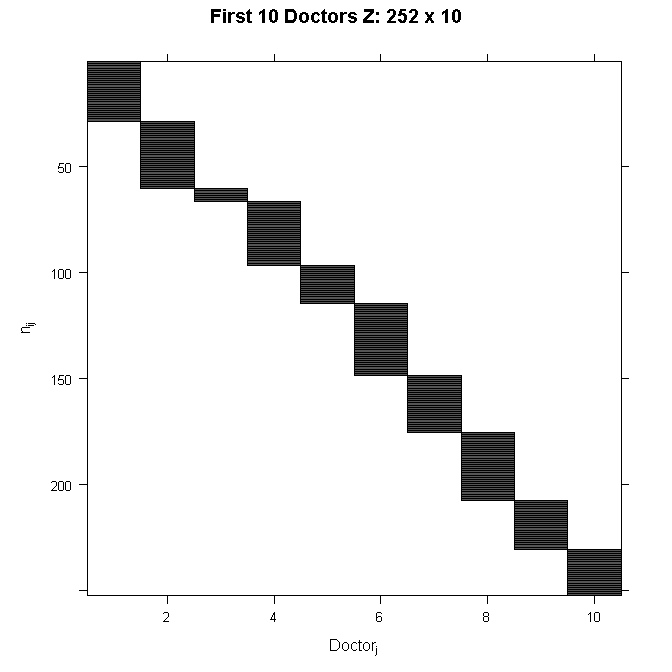
In order to see the structure in more detail, we could also zoom in on just the first 10 doctors. The filled space indicates rows of observations belonging to the doctor in that column, whereas the white space indicates not belonging to the doctor in that column.
If we estimated it, \(\boldsymbol{u}\) would be a column vector, similar to \(\boldsymbol{\beta}\). However, in classical statistics, we do not actually estimate \(\boldsymbol{u}\). Instead, we nearly always assume that:
$$ \boldsymbol{u} \sim \mathcal{N}(\mathbf{0}, \mathbf{G}) $$
Which is read: “\(\boldsymbol{u}\) is distributed as normal with mean zero and variance \(\mathbf{G}\) “. Where \(\mathbf{G}\) is the variance-covariance matrix of the random effects. Because we directly estimated the fixed effects, including the fixed effect intercept, random effect complements are modeled as deviations from the fixed effect, so they have mean zero. The random effects are just deviations around the value in \(\boldsymbol{\beta}\), which is the mean. So what is left to estimate is the variance. Because our example only had a random intercept, \(\mathbf{G}\) is just a \(1 \times 1\) matrix, the variance of the random intercept (i.e. \(\mathbf{G}= [\sigma^{2}_{int}]\) ). However, it can be larger. For example, suppose that we had a random intercept and a random slope, then
$$ \mathbf{G} = \begin{bmatrix} \sigma^{2}_{int} & \sigma^{2}_{int,slope} \\ \sigma^{2}_{int,slope} & \sigma^{2}_{slope} \end{bmatrix} $$
Because \(\mathbf{G}\) is a variance-covariance matrix, we know that it should have certain properties. In particular, we know that it is square, symmetric, and positive semidefinite. We also know that this matrix has redundant elements. For a \(q \times q\) matrix, there are \(\frac{q(q+1)}{2}\) unique elements. To simplify computation by removing redundant effects and ensure that the resulting estimate matrix is positive definite, rather than model \(\mathbf{G}\) directly, we estimate \(\boldsymbol{\theta}\) (e.g., a triangular Cholesky factorization \(\mathbf{G} = \mathbf{LDL^{T}}\)). \(\boldsymbol{\theta}\) is not always parameterized the same way, but you can generally think of it as representing the random effects. It is usually designed to contain non redundant elements (unlike the variance covariance matrix) and to be parameterized in a way that yields more stable estimates than variances (such as taking the natural logarithm to ensure that the variances are positive). Regardless of the specifics, we can say that
$$ \mathbf{G} = \sigma(\boldsymbol{\theta}) $$
In other words, \(\mathbf{G}\) is some function of \(\boldsymbol{\theta}\). So we get some estimate of \(\boldsymbol{\theta}\) which we call \(\hat{\boldsymbol{\theta}}\). Various parameterizations and constraints allow us to simplify the model for example by assuming that the random effects are independent, which would imply the true structure is
$$ \mathbf{G} = \begin{bmatrix} \sigma^{2}_{int} & 0 \\ 0 & \sigma^{2}_{slope} \end{bmatrix} $$
The final element in our model is the variance-covariance matrix of the residuals, \(\mathbf{\varepsilon}\) or the variance-covariance matrix of conditional distribution of \((\mathbf{y} | \boldsymbol{\beta} ; \boldsymbol{u} = u)\). The most common residual covariance structure is
$$ \mathbf{R} = \boldsymbol{I\sigma^2_{\varepsilon}} $$
where \(\mathbf{I}\) is the identity matrix (diagonal matrix of 1s) and \(\sigma^2_{\varepsilon}\) is the residual variance. This structure assumes a homogeneous residual variance for all (conditional) observations and that they are (conditionally) independent. Other structures can be assumed such as compound symmetry or autoregressive. The \(\mathbf{G}\) terminology is common in SAS, and also leads to talking about G-side structures for the variance covariance matrix of random effects and R-side structures for the residual variance covariance matrix.
So the final fixed elements are \(\mathbf{y}\), \(\mathbf{X}\), \(\mathbf{Z}\), and \(\boldsymbol{\varepsilon}\). The final estimated elements are \(\hat{\boldsymbol{\beta}}\), \(\hat{\boldsymbol{\theta}}\), and \(\hat{\mathbf{R}}\). The final model depends on the distribution assumed, but is generally of the form:
$$ (\mathbf{y} | \boldsymbol{\beta}; \boldsymbol{u} = u) \sim \mathcal{N}(\boldsymbol{X\beta} + \boldsymbol{Z}u, \mathbf{R}) $$
We could also frame our model in a two level-style equation for the \(i\)-th patient for the \(j\)-th doctor. There we are working with variables that we subscript rather than vectors as before. The level 1 equation adds subscripts to the parameters \(\beta\)s to indicate which doctor they belong to. Turning to the level 2 equations, we can see that each \(\beta\) estimate for a particular doctor, \(\beta_{pj}\), can be represented as a combination of a mean estimate for that parameter, \(\gamma_{p0}\), and a random effect for that doctor, (\(u_{pj}\)). In this particular model, we see that only the intercept (\(\beta_{0j}\)) is allowed to vary across doctors because it is the only equation with a random effect term, (\(u_{0j}\)). The other \(\beta_{pj}\) are constant across doctors.
$$ \begin{array}{l l} L1: & Y_{ij} = \beta_{0j} + \beta_{1j}Age_{ij} + \beta_{2j}Married_{ij} + \beta_{3j}Sex_{ij} + \beta_{4j}WBC_{ij} + \beta_{5j}RBC_{ij} + e_{ij} \\ L2: & \beta_{0j} = \gamma_{00} + u_{0j} \\ L2: & \beta_{1j} = \gamma_{10} \\ L2: & \beta_{2j} = \gamma_{20} \\ L2: & \beta_{3j} = \gamma_{30} \\ L2: & \beta_{4j} = \gamma_{40} \\ L2: & \beta_{5j} = \gamma_{50} \end{array} $$
Substituting in the level 2 equations into level 1, yields the mixed model specification. Here we grouped the fixed and random intercept parameters together to show that combined they give the estimated intercept for a particular doctor.
$$ Y_{ij} = (\gamma_{00} + u_{0j}) + \gamma_{10}Age_{ij} + \gamma_{20}Married_{ij} + \gamma_{30}SEX_{ij} + \gamma_{40}WBC_{ij} + \gamma_{50}RBC_{ij} + e_{ij} $$
References
- Fox, J. (2008). Applied Regression Analysis and Generalized Linear Models, 2nd ed. Sage Publications.
- McCullagh, P, & Nelder, J. A. (1989). Generalized Linear Models, 2nd ed. Chapman & Hall/CRC Press.
- Snijders, T. A. B. & Bosker, R. J. (2012). Multilevel Analysis, 2nd ed. Sage Publications.
- Singer, J. D. & Willett, J. B. (2003). Applied Longitudinal Data Analysis: Modeling Change and Event Occurrence. Oxford University Press.
- Pinheiro, J. & Bates, D. (2009). Mixed-Effects Models in S and S-Plus. 2nd printing. Springer.
- Galecki, A. & Burzykowski, T. (2013). Linear Mixed-Effects Models Using R. Springer.
- Skrondal, A. & Rabe-Hesketh, S. (2004). Generalized Latent Variable Modeling: Multilevel, longitudinal, and structural equation models. Chapman & Hall/CRC Press.
- Gelman, A. & Hill, J. (2006). Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge University Press.
- Gelman, A., Carlin, J. B., Stern, H. S. & Rubin, D. B. (2003). Bayesian Data Analysis, 2nd ed. Chapman & Hall/CRC.
