Introduction to Power Analysis Seminar

The main seminar page is here.

Introduction

Welcome to the first of three seminars on power analysis

This is the introductory seminar and will discuss, on a conceptual and mechanical level, many of the factors that affect power.
We encourage everyone to review the material in this seminar before moving onto the intermediate power seminar, as that seminar builds on the material presented in this one.

Power is the probability of detecting an effect, given that the effect is really there. In other words, it is the probability of rejecting the null hypothesis when it is in fact false.

Example: Drug A and placebo
run experiment 1000 times, holding everything constant
If the power was in fact .8, 800 times out of the 1000, we would see a statistically significant difference between the two groups.

Power is a probability, not a certainty: just because you have a power of .8 or .9 does not guarantee that you will obtain a statistically significant result.

Several of reasons why one might do a power analysis:

determine the necessary number of subjects needed to detect an effect of a given size
trying to find the absolute, bare minimum number of subjects needed in the study is usually not a good idea (pop quiz at the end of the seminar)
determine power, given an effect size and the number of subjects available (to decide if you should do the study)
In most cases, there is really no point to conducting a study that is seriously underpowered.
often required as part of a grant proposal
often just part of doing good research
Power analysis as a planning tool: A power analysis is a good way of making sure that you have thought through every aspect of the study and the statistical analysis before you start collecting data.

Some limitations of power analysis:

typically does not generalize very well
might suggest a number of subjects that is inadequate for the statistical procedure
Best case scenario: most important limitation is that a standard power analysis gives you a best case scenario estimate of the necessary number of subjects needed to detect the effect. In most cases, this best case scenario is based on assumptions and educated guesses. If any of these assumptions or guesses are incorrect, you may have less power than you need to detect the effect. One of the assumptions is that all of the assumptions of the statistical procedure have been met.
often get a range of the number of subjects needed, not a precise number
can’t blindly accept the number output by the power analysis program – more on this later

Power is not the only consideration when determining the necessary sample size:

different reasons for conducting an analysis: coefficient different from zero versus precise point estimate
statistical procedure that is going to be used (maximum likelihood techniques usually need a large number of subjects)
the representativeness of the sample and the generalizability of the results (may need a larger N to increase the representativeness and hence the generalizability of the results)
how many statistical tests will be run on the data set

Most of what is in this presentation does not readily apply to people who are developing a sampling plan for a survey or psychometric analyses.

Definitions

Before we move on, let s make sure we are all using the same definitions.

power is the probability of detecting a true effect, given that the effect exists
most recommendations for power fall between .8 and .9
effect size
- the current APA manual has a list of more than 15 effect sizes
- one of the simplest definitions is that an effect size is the difference of two group means divided by the pooled standard deviation.
- example: suppose the mean of the outcome variable for the drug A group was 10 and it was 5 for the placebo group. If the pooled standard deviation was 2.5, we would have and effect size which is equal to (10-5)/2.5 = 2 (which is a large effect size).
statistically significance versus clinically relevant : important when estimating effect size for the power analysis
Other definitions that we will need later on include Type I and II errors and alpha inflation. These are discussed on the main seminar page.

When discussing statistical power, we have four inter-related concepts: alpha, effect size, sample size and power.

These four things are related such that each is a function of the other three.
Increasing alpha (for example, from .01 to .05), effect size or sample size will increase power.
Not all increases are created equal.

Let’s take a quick look at a standard power graph.

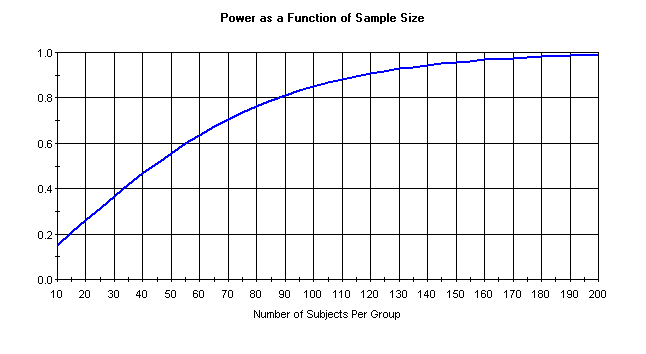
Image ips1
What we like about these kinds of graphs, is that they make clear the diminishing returns you get for adding more and more subjects.

For example, let s say that we have only 10 subjects per group. We can see that we have a power of .15, which is really, really low. We add 50 subjects per group, now we have a power of .6, an increase of .45. However, if we started with 100 subjects per group (which would give me a power of about .8) and added 50 per group, we would have a power of .95, an increase of only .15. So each additional subject gives you less additional power.

Going back to our power recommendations, we can see that increasing from .8 to .9 can be very costly (an additional 30 subjects per group).

Knowing your research project

As we mentioned before, one of the big benefits of doing a power analysis is making sure that you have thought through every detail of the research project. In general terms, there are three topic areas that you need to consider when doing a power analysis.

substantive area, experimental design issues and statistical technique

Want to be familiar with the statistical procedure before doing a power analysis.

Make sure that you can use the necessary software.

Do your research on experimental design issues, the statistical technique and software, before you do your research project.

What you need to know to do a power analysis

In this section we will discuss some of the actual quantities that you need to know to do a power analysis for some simple statistics. The point is to give you a flavor of the types of things that you will need to know (or guess at) in order to be ready for a power analysis.

For an independent samples t test, you will need to know the population means of the two groups (or the difference between the means), and the population standard deviations of the two groups.
We always recommend that you use several different values, such as decreasing the difference in the means and increasing the standard deviations, so that you get a range of values for the number of necessary subjects.

In SPSS Sample Power, we would have a screen that looks like the one below.

We would need a total of 70 subjects (35 per group) to have a power of .91 if we had a mean of 5 and a standard deviation of 2.5 in the drug A group, and a mean of 3 and a standard deviation of 2.5 in the placebo group.
If we decreased the difference in the means and increased the standard deviations such that for the drug A group, we had a mean of 4.5 and a standard deviation of 3, and for the placebo group a mean of 3.5 and a standard deviation of 3 (decrease the difference in means from 2 to 1 and increase the standard deviation from 2.5 to 3), we would need 190 subjects per group, or a total of 380 subjects, to have a power of .9.
Seemingly small differences in means and standard deviations can have a huge effect on the number of subjects required.

Image t-test

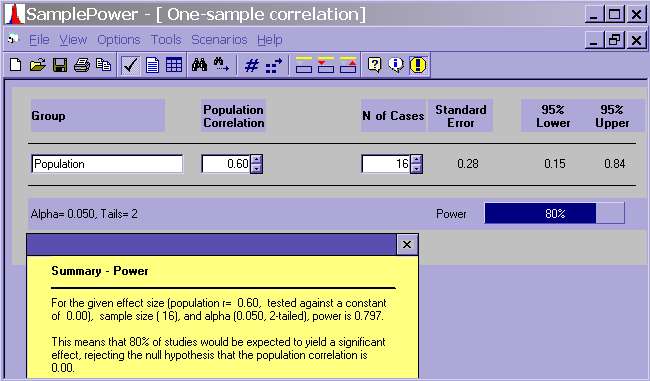
For a correlation, you need to know/guess at the correlation in the population.

If you guess that the population correlation is .6, a power analysis would suggest (with an alpha of .05 and for a power of .8) that you would need 16 subjects.
Correlation is a large N procedure
N = 16 is pretty low.
a population correlation of .6 is pretty high, especially in the social sciences.
the power analysis assumes that all of the assumptions of the correlation have been met (outliers, restriction of range, linear relationship between the variables, etc.).

Image corr

For a chi-square test, you will need to know the proportion positive for both populations (i.e., rows and columns). Please see the main seminar page for a description of what is involved here.

For an ordinary least squares regression, you would need to know things like the R² for the full and reduced model.

For a simple logistic regression analysis with only one continuous predictor variable, you would need to know the probability of a positive outcome (i.e., the probability that the outcome equals 1) at the mean of the predictor variable, and the probability of a positive outcome at one standard deviation above the mean of the predictor variable.

Obtaining the necessary numbers to do a power analysis

There are at least three ways to guestimate the values that are needed to do a power analysis: a literature review, a pilot study and using Cohen s recommendations.

pros and cons of each of these three methods
focus on determining effect size

Literature review:

Similar studies
meta-analysis to get a robust effect size

Limitations to a literature review:

oftentimes there are no studies similar enough to your study to get a good estimate of the effect size

Pilot studies:

rough estimate of the effect size, as well as a rough estimate of the variability in your measures
ideas about where missing data might occur, and hopefully ideas about how to minimize the amount of missing
identify coding problems, setting up the data base, and inputting the data for a practice analysis

Limitations to the information that you can get from a pilot study:

When estimating effect sizes based on nonsignificant results, the effect size estimate will necessarily have an increased error (not a very precise estimate).
The effect size estimate that you obtain may be unduly influenced by some peculiarity of the small sample.

Despite these limitations, we strongly encourage researchers to conduct a pilot study.

The opportunity to identify and correct bugs before collecting the real data is often invaluable.
Because of the number of values that need to be guestimated in a power analysis, the precision of any one of these values is not that important. If you can estimate the effect size to within 10% or 20% of the true value, that is probably sufficient for you to conduct a meaningful power analysis.

Cohen s recommendations:

Many researchers (including Cohen) consider the use of such recommendations as a last resort, when a thorough literature review has failed to reveal any useful numbers and a pilot study is not possible or feasible.

– Small effect: 1% of the variance; d = 0.25 (too small to detect other than statistically; lower limit of what is clinically relevant)

– Medium effect: 6% of the variance; d = 0.5 (apparent with careful observation)

– Large effect: at least 15% of the variance; d = 0.8 (apparent with a superficial glance; unlikely to be the focus of research because it is too obvious)

According to Keppel and Wickens (2004), when you really have no idea what the effect size is, go with the smallest effect size of practical value. In other words, you need to know how small of a difference is meaningful to you.
Research suggests that most researchers are overly optimistic about the effect sizes in their research, and that most research studies are under powered.

Factors that affect power

From the preceding discussion, you might be starting to think that the number of subjects and the effect size are the most important factors, or even the only factors, that affect power.

There are at least a dozen other factors that can influence the power of a study, and many of these factors should be considered not only from the point of doing a power analysis, but also as part of doing good research.
The first couple of factors that we will discuss are more "mechanical" ways of increasing power (e.g., alpha level, sample size and effect size). After that, the discussion will turn to more methodological issues that affect power.

1. Alpha level: One obvious way to increase your power is to increase your alpha (from .05 to say, .1). This might be more appropriate for a pilot study rather than the actual study. Reducing alpha from .05 to .01 reduces power (crude attempt to ensure that results are clinically relevant).

2. Sample size: A second obvious way to increase power is simply collect data on more subjects. Subjects can be "expensive"; add some to the control group.

3. Effect size: Another obvious way to increase your power is to increase the effect size (often by increasing the experimental manipulation).

4. Experimental task: If you can not increase the experimental manipulation, perhaps you can change the experimental task, if there is one.

5. Response variable: How you measure your response variable(s) is just as important as what task you have the subject perform. You want to use a measure that is as high in sensitivity and low in measurement error as is possible. Minimizing the measurement error in your predictor variables will also help increase your power. Modify the procedure so that all instructions are clear and question are unambiguous to all subjects. Use direct instead of indirect measures. While multiple DV’s are very good methodologically and provides marked benefits for certain analyses and missing data, it does complicate the power analysis. The next seminar will discuss this issue.

6. Experimental design: Another thing to consider is that some types of experimental designs are more powerful than others (repeated measures).

7. Groups: Another point to consider is the number and types of groups that you are using. Drug example with 4 groups: placebo, low dose, medium dose and high dose. Reduce the number of groups and/or make comparisons among the extremes. May affect generalizability.

8. Statistical procedure: Changing the type of statistical analysis may also help increase power, especially when some of the assumptions of the test are violated.

Maxwell and Delaney (2004) noted that Even when ANOVA is robust, it may not provide the most powerful test available when its assumptions have been violated. In particular, violations of assumptions regarding independence, normality and heterogeneity can reduce power. In such cases, nonparametric alternatives may be more powerful.
You have to know about the statistical procedure and its assumptions.

9. Statistical model: You can also modify the statistical model. For example, interactions often require more power than main effects; if you don’t have much power, you may need to use a main effects model. Consider using covariates or blocking variables. Ideally, both covariates and blocking variables reduce the variability in the response variable, but these kinds of variables can be difficult to find.

10. Modify response variable: Besides modifying your statistical model, you might also try modifying your response variable. Possible benefits of this strategy include reducing extreme scores and/or meeting the assumptions of the statistical procedure. Categorizing the response variable can be problematic.

11. Purpose of the study: Different researchers have different reasons for conducting research. Drug A example: estimate different from 0 versus precise point estimate.

Tversky and Kahneman (1971) pointed out that we often need more subjects in a replication study than were in the original study. They also noted that researchers are often too optimistic about how much power they really have.
Most power analysis programs do not take into account the purpose of the study; rather, they assume that you are trying to determine if the estimate is different from 0.
Tversky and Kahneman also claim that researchers too readily assign causal reasons to explain differences between studies, instead of sampling error. They also mentioned that researchers tend to underestimate the impact of sampling and think that results will replicate more often than is the case.

12. Missing data: A final point that we would like to make here regards missing data. Do everything possible to minimize missing data. Casewise deletion, which is the default setting in most statistical packages, is one of the biggest contributors to loss of power. Poor imputation methods can greatly reduce power.

Conclusions:

Most of these issues are not black and white .
There is a close relationship between the experimental design, the statistical analysis and power.

Cautions about small sample sizes and sampling variation

Issues that frequently arise when using small samples:

Considerations of time and effort argue for running as few subjects as possible versus difficulties associated with small sample sizes
One obvious problem with small sample sizes is that they have low power. This means that you need to have a large effect size to detect anything.
You will also have fewer options with respect to appropriate statistical procedures, as many common procedures, such as correlations, logistic regression and multilevel modeling, are not appropriate with small sample sizes.
One is also more likely to violate the assumptions of the statistical procedure that is used (especially assumptions like normality). In most cases, the statistical model must be smaller when the data set is small.
Interaction terms, which often test interesting hypotheses, are frequently the first casualties.
Generalizability of the results may also be comprised.
Missing data are also more problematic; there are a reduced number of imputations methods available to you, and these are not considered to be desirable imputation methods (such as mean imputation).

Sampling variation:

While the issue of sampling variability is relevant to all research, it is especially relevant to studies with small sample sizes.
- To quote Murphy and Myors (2004, page 59), The lack of attention to power analysis (and the deplorable habit of placing too much weight on the results of small sample studies) are well documented in the literature, and there is no good excuse to ignore power in designing studies.
In an early article entitled The Law of Small Numbers, Tversky and Kahneman (1971) stated that many researchers act like the Law of Large Numbers applies to small numbers. People often believe that small samples are more representative of the population than they really are.

Underpowered studies:

There is usually no point to conducting an underpowered study.
Underpowered studies can cause chaos in the literature because studies that are similar methodologically may report conflicting results.

Software

We will briefly discuss some of the programs that you can use to assist you with your power analysis. Most programs are fairly easy to use, but you still need to know effect sizes, means, standard deviations, etc.

Specialty packages: SPSS Sample Power, PASS and Optimal Design
General use packages: SAS proc power and Stata sampsi, user written commands, Statistica add-on module
free programs on the web
Mplus

Multiplicity

This issue of multiplicity arises when a researcher has more than one outcome of interest in a given study.

While it is often good methodological practice to have more than one measure of the response variable of interest, additional response variables mean more statistical tests need to be conducted on the data set, and this leads to question of experimentwise alpha control.
Example: Drug A and placebo
The question is how to control the Type I error (AKA false alarm) rate. Most researchers are familiar with Bonferroni correction, which calls for dividing the prespecified alpha level (usually .05) by the number of tests to be conducted. In our example, we would have .05/3 = .0167. Hence, .0167 would be our new critical alpha level, and statistics with a p value greater than .0167 would be classified as not statistically significant.
It is well-known that the Bonferroni correction is very conservative, so in our next seminar, we will discuss other ways of adjusting the alpha level.

Afterthoughts: A post-hoc power analysis

Just say "No!" to post-hoc analyses. There are many reasons, both mechanical and theoretical, why good researchers should not do post-hoc power analyses.

Excellent summaries can be found in Hoenig and Heisey (2001) The Abuse of Power: The Pervasive Fallacy of Power Calculations for Data Analysis and Levine and Ensom (2001) Post Hoc Power Analysis: An Idea Whose Time Has Passed?.
As Hoenig and Heisey show, power is mathematically directly related to the p-value; hence, calculating power once you know the p-value associated with a statistic adds no new information.
Furthermore, as Levine and Ensom clearly explain, the logic underlying post-hoc power analyses is fundamentally flawed.

How good was your guess about the means and standard deviations of your variables? If the variability in your measures is substantially higher than you thought, you may want to use different measures in future research.

Conclusions

Conducting research is kind of like buying a car.
Don’t be afraid of what you don’t know. Get in there and try it BEFORE you collect your data.
Power analysis = planning (for all things)
Correcting things is easy at this stage; after you collect your data, all you can do is damage control.
UCLA researchers are always welcome and strongly encouraged to come into our walk-in consulting and discuss their research before they begin the project.

The take-home message from this seminar is do your research before you do your research.