R Textbook Examples Applied Longitudinal Data Analysis: Modeling Change and Event Occurrence by Judith D. Singer and John B. Willett Chapter 11: Fitting basic discrete-time hazard models
The examples on the page were written in R version 2.4.1. This page requires package survival.
library(survival)
Figure 11.1, page 359
firstsex<-read.table("https://stats.idre.ucla.edu/stat/examples/alda/firstsex.csv", sep=",", header=T)
ts0 <- survfit( Surv(time, 1-censor)~ 1, conf.type="none", subset=(pt==0), data=firstsex)
ts1 <- survfit( Surv(time, 1-censor)~ 1, conf.type="none", subset=(pt==1), data=firstsex)
h0<-ts0$n.event/ts0$n.risk
h1<-ts1$n.event/ts1$n.risk
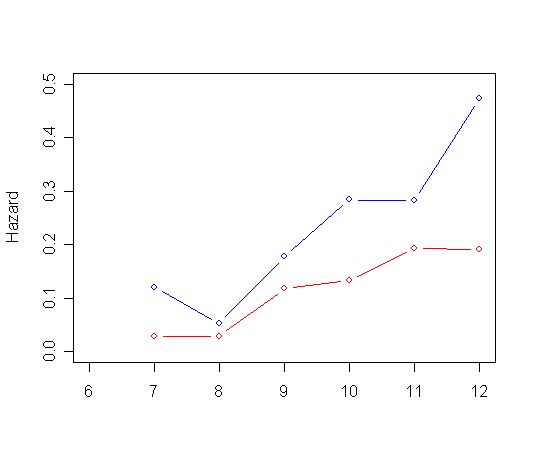
plot(ts0$time, h0, type="l", ylab="Estimated Hazard probability", xlab="Grade",
ylim=c(0.0, 0.5), xlim=c(6, 12), col="red")
par(new=T)
plot(ts1$time, h1, type="l", ylab=" ", ylim=c(0.0, 0.5), xlim=c(6, 12), xlab="", col="blue")
plot(ts0$time, ts0$surv, type="l", ylab="Estimated Survival Function", xlab="Grade",
ylim=c(0.0, 1.0), xlim=c(6, 12), col="red")
par(new=T)
plot(ts1$time, ts1$surv, type="l", ylab=" ", ylim=c(0.0, 1.0), xlim=c(6, 12), xlab="", col="blue")
abline(h=c(.5), lty=2)
Table 11.1, page 360. We will do create the table in two parts. The first part is based on the result from previous example.
tab11.1.0<-cbind(time=ts0$time, nleft=ts0$n.risk, failed=ts0$n.event, hazard=h0, survival=ts0$surv) tab11.1.1<-cbind(time=ts1$time, nleft=ts1$n.risk, failed=ts1$n.event, hazard=h1, survival=ts1$surv) tab11.1 <-rbind(tab11.1.0, tab11.1.1) tab11.1
time nleft failed hazard survival [1,] 7 72 2 0.02777778 0.9722222 [2,] 8 70 2 0.02857143 0.9444444 [3,] 9 68 8 0.11764706 0.8333333 [4,] 10 60 8 0.13333333 0.7222222 [5,] 11 52 10 0.19230769 0.5833333 [6,] 12 42 8 0.19047619 0.4722222 [7,] 7 108 13 0.12037037 0.8796296 [8,] 8 95 5 0.05263158 0.8333333 [9,] 9 90 16 0.17777778 0.6851852 [10,] 10 74 21 0.28378378 0.4907407 [11,] 11 53 15 0.28301887 0.3518519 [12,] 12 38 18 0.47368421 0.1851852
tsall <- survfit( Surv(time, 1-censor)~ 1, conf.type="none", data=firstsex)
h<-tsall$n.event/tsall$n.risk
tab11.1.all<-cbind(time=tsall$time, nleft=tsall$n.risk, failed=tsall$n.event, hazard=h, survival=tsall$surv)
tab11.1.all
time nleft failed hazard survival
[1,] 7 180 15 0.08333333 0.9166667
[2,] 8 165 7 0.04242424 0.8777778
[3,] 9 158 24 0.15189873 0.7444444
[4,] 10 134 29 0.21641791 0.5833333
[5,] 11 105 25 0.23809524 0.4444444
[6,] 12 80 26 0.32500000 0.3000000
Figure 11.2, page 363
We will use the variables created for the previous example containing the hazard function created for Figure 11.1 in order to create the estimated odds and the estimated logit(hazard).
odds0<-h0/(1-h0)
odds1<-h1/(1-h1)
logith0<-log(odds0)
logith1<-log(odds1)
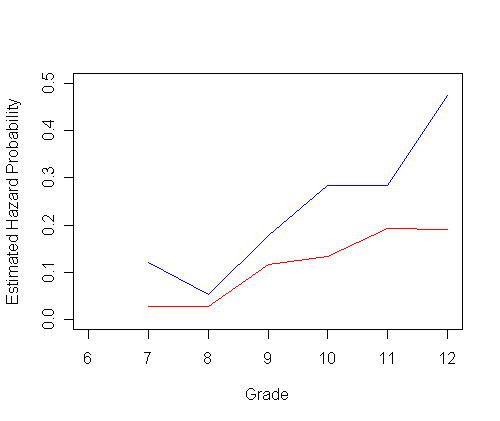
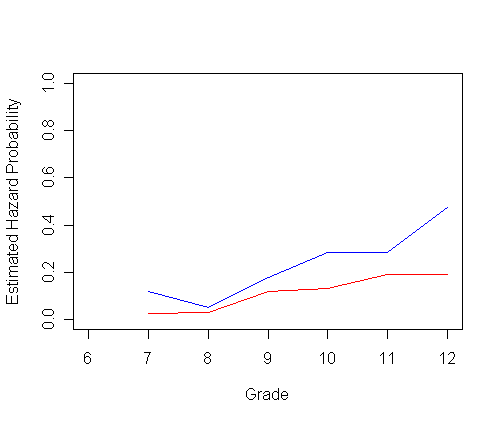
plot(ts0$time, h0, type="l", ylab="Estimated Hazard Probability", xlab="Grade",
ylim=c(0.0, 1), xlim=c(6, 12), col="red")
par(new=T)
plot(ts1$time, h1, type="l", ylab=" ", ylim=c(0.0, 1), xlim=c(6, 12), xlab="", col="blue")
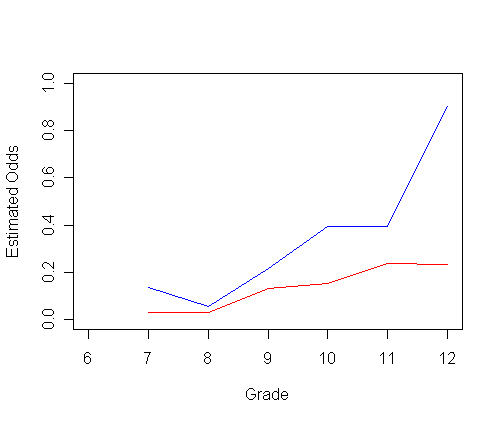
plot(ts0$time, odds0, type="l", ylab="Estimated Odds", xlab="Grade",
ylim=c(0,1), xlim=c(6, 12), col="red")
par(new=T)
plot(ts1$time, odds1, type="l", ylab=" ", ylim=c(0, 1), xlim=c(6, 12), xlab="", col="blue")
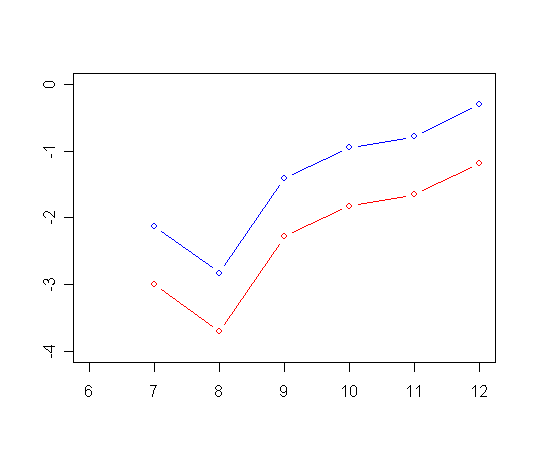
plot(ts0$time, logith0, type="l", ylab="Estimated Logit", xlab="Grade",
ylim=c(-4, 0), xlim=c(6, 12), col="red")
par(new=T)
plot(ts1$time, logith1, type="l", ylab=" ", ylim=c(-4, 0), xlim=c(6, 12), xlab="", col="blue")
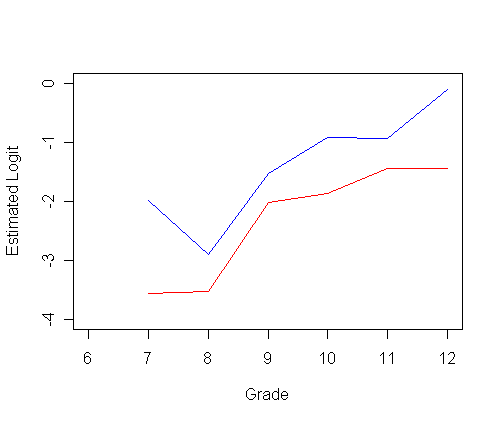
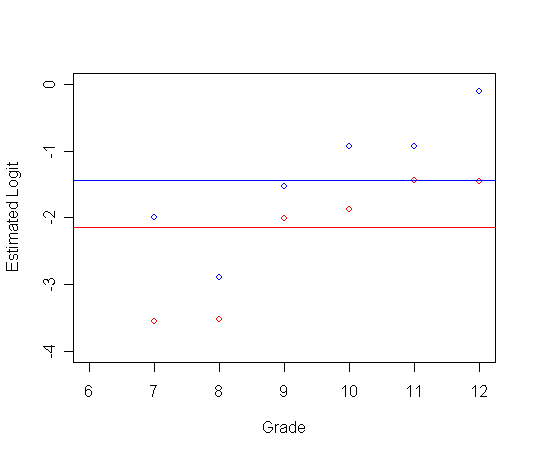
Figure 11.3 on page 366.
Panel A: logit hazard is horizontal with time.
firstsex.pp<-read.table("https://stats.idre.ucla.edu/stat/examples/alda/firstsex_pp.csv", sep=",", header=T)
afit <- glm(event ~ pt, family="binomial", data=firstsex.pp)
summary(afit)
Call:
glm(formula = event ~ pt, family = "binomial", data = firstsex.pp)
Deviance Residuals:
Min 1Q Median 3Q Max
-0.6532 -0.6532 -0.4696 -0.4696 2.1258
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.1493 0.1714 -12.539 < 2e-16 ***
pt 0.7131 0.2084 3.421 0.000623 ***
t<-data.frame(afit$coefficients)
p0<-t[1,1]
p1<-p0+t[2,1]
firstsex<-read.table("https://stats.idre.ucla.edu/stat/examples/alda/firstsex.csv", sep=",", header=T)
ts0 <- survfit( Surv(time, 1-censor)~ 1, conf.type="none", subset=(pt==0), data=firstsex)
ts1 <- survfit( Surv(time, 1-censor)~ 1, conf.type="none", subset=(pt==1), data=firstsex)
h0<-ts0$n.event/ts0$n.risk
h1<-ts1$n.event/ts1$n.risk
odds0<-h0/(1-h0)
odds1<-h1/(1-h1)
logith0<-log(odds0)
logith1<-log(odds1)
plot(ts0$time, logith0, type="p", ylab="Estimated Logit", xlab="Grade",
ylim=c(-4, 0), xlim=c(6, 12), col="red")
par(new=T)
plot(ts1$time, logith1, type="p", ylab=" ", ylim=c(-4, 0), xlim=c(6, 12), xlab="", col="blue")
abline(h=c(p0), lty=1, col="red")
abline(h=c(p1), lty=1, col="blue")
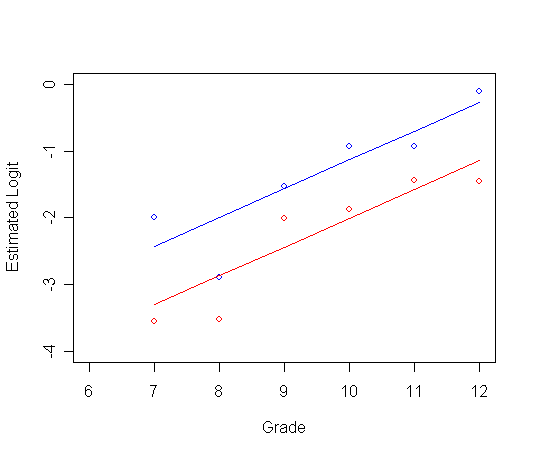
Panel B: logit hazard is linear with time
afit2<-glm(event~pt + period, family="binomial", data=firstsex.pp)
summary(afit2)
Call:
glm(formula = event ~ pt + period, family = "binomial", data = firstsex.pp)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.0653 -0.6177 -0.4128 -0.3329 2.5813
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -6.30534 0.67034 -9.406 < 2e-16 ***
pt 0.87544 0.21696 4.035 5.46e-05 ***
period 0.43003 0.06407 6.712 1.92e-11 ***
t<-data.frame(afit2$coefficients)
y0<-t[1,1] + t[3,1]*ts0$time
y1<-t[1,1] + t[2,1] + t[3,1]*ts0$time
plot(ts0$time, logith0, type="p", ylab="Estimated Logit", xlab="Grade",
ylim=c(-4, 0), xlim=c(6, 12), col="red")
par(new=T)
plot(ts1$time, logith1, type="p", ylab=" ", ylim=c(-4, 0), xlim=c(6, 12), xlab="", col="blue")
par(new=T)
plot(ts1$time, y0, type="l", ylab=" ", ylim=c(-4, 0), xlim=c(6, 12), xlab="", col="red")
par(new=T)
plot(ts1$time, y1, type="l", ylab=" ", ylim=c(-4, 0), xlim=c(6, 12), xlab="", col="blue")
Panel C: Logit hazard is completely general with time.
afit3<-glm(event~pt + factor(period), family="binomial", data=firstsex.pp) summary(afit3)
glm(formula = event ~ pt + factor(period), family = "binomial",
data = firstsex.pp)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.0508 -0.6617 -0.4411 -0.3126 2.7293
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.9943 0.3175 -9.431 < 2e-16 ***
pt 0.8736 0.2174 4.018 5.86e-05 ***
factor(period)8 -0.7058 0.4728 -1.493 0.135514
factor(period)9 0.7132 0.3519 2.027 0.042667 *
factor(period)10 1.1717 0.3452 3.394 0.000689 ***
factor(period)11 1.3401 0.3588 3.735 0.000188 ***
factor(period)12 1.8153 0.3674 4.941 7.78e-07 ***
t<-data.frame(cbind(y=afit3$linear.predictors, time=firstsex.pp$period, pt=firstsex.pp$pt))
t0<-t[t$pt==0,]
t0<-t0[order(t0$time),]
t1<-t[t$pt==1,]
t1<-t1[order(t1$time),]
plot(ts0$time, logith0, type="p", ylab="Estimated Logit", xlab="Grade",
ylim=c(-4, 0), xlim=c(6, 12), col="red")
par(new=T)
plot(ts1$time, logith1, type="p", ylab=" ", ylim=c(-4, 0), xlim=c(6, 12), xlab="", col="blue")
par(new=T)
plot(t0$time, t0$y, type="l", ylab=" ", ylim=c(-4, 0), xlim=c(6, 12), xlab="", col="red")
par(new=T)
plot(t1$time, t1$y, type="l", ylab=" ", ylim=c(-4, 0), xlim=c(6, 12), xlab="", col="blue")
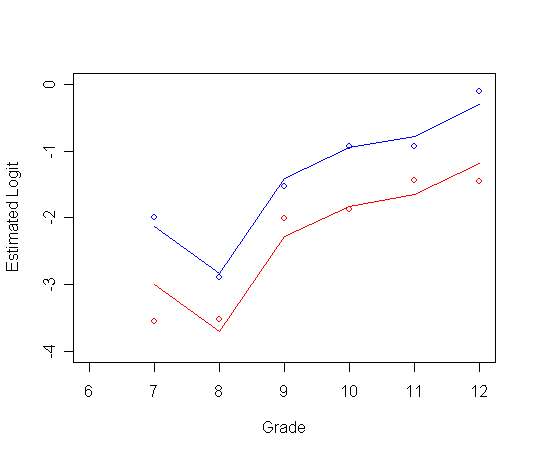
Figure 11.4, page 374
Panel A:
afit3<-glm(event~pt + factor(period), family="binomial", data=firstsex.pp) t<-data.frame(cbind(y=afit3$linear.predictors, time=firstsex.pp$period, pt=firstsex.pp$pt)) t0<-t[t$pt==0,] t0<-t0[order(t0$time),] t1<-t[t$pt==1,] t1<-t1[order(t1$time),] plot(t0$time, t0$y, type="b", ylab=" ", ylim=c(-4, 0), xlim=c(6, 12), xlab="", col="red") par(new=T) plot(t1$time, t1$y, type="b", ylab=" ", ylim=c(-4, 0), xlim=c(6, 12), xlab="", col="blue")
Panel B:
afit4<-glm(event~pt + factor(period) + pt*factor(period), family="binomial", data=firstsex.pp) t<-data.frame(cbind(y=exp(afit4$linear.predictors), time=firstsex.pp$period, pt=firstsex.pp$pt)) t0<-t[t$pt==0,] t0<-t0[order(t0$time),] t1<-t[t$pt==1,] t1<-t1[order(t1$time),] plot(t0$time, t0$y, type="b", ylab="Odds", ylim=c(0, 1), xlim=c(6, 12), xlab="", col="red") par(new=T) plot(t1$time, t1$y, type="b", ylab=" ", ylim=c(0, 1), xlim=c(6, 12), xlab="", col="blue")
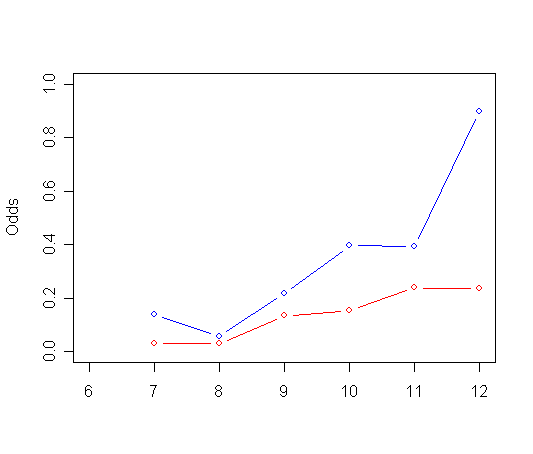
Panel C:
t<-data.frame(cbind(y=afit4$fitted.values, time=firstsex.pp$period, pt=firstsex.pp$pt)) t0<-t[t$pt==0,] t0<-t0[order(t0$time),] t1<-t[t$pt==1,] t1<-t1[order(t1$time),] plot(t0$time, t0$y, type="b", ylab="Hazard", ylim=c(0, .5), xlim=c(6, 12), xlab="", col="red") par(new=T) plot(t1$time, t1$y, type="b", ylab=" ", ylim=c(0, .5), xlim=c(6, 12), xlab="", col="blue")
Table 11.3, page 386. Notice that in order to do the deviance test, sometimes we have to run the model multiple times, one for each variable being tested since the variable being tested has to appear at the end of the model.
Model A:
modelA<-glm(event~factor(period) - 1, family="binomial", data=firstsex.pp) summary(modelA)
Call:
glm(formula = event ~ factor(period) - 1, family = "binomial",
data = firstsex.pp)
Deviance Residuals:
Min 1Q Median 3Q Max
-0.8866 -0.6984 -0.4172 -0.2945 2.5140
Coefficients:
Estimate Std. Error z value Pr(>|z|)
factor(period)7 -2.3979 0.2697 -8.892 < 2e-16 ***
factor(period)8 -3.1167 0.3862 -8.071 7.00e-16 ***
factor(period)9 -1.7198 0.2217 -7.759 8.56e-15 ***
factor(period)10 -1.2867 0.2098 -6.133 8.60e-10 ***
factor(period)11 -1.1632 0.2291 -5.076 3.85e-07 ***
factor(period)12 -0.7309 0.2387 -3.062 0.0022 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1139.53 on 822 degrees of freedom
Residual deviance: 651.96 on 816 degrees of freedom
AIC: 663.96
Number of Fisher Scoring iterations: 5
Model B:
modelB<-glm(event~factor(period) + pt - 1, family="binomial", data=firstsex.pp) summary(modelB)
Call:
glm(formula = event ~ factor(period) + pt - 1, family = "binomial",
data = firstsex.pp)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.0508 -0.6617 -0.4411 -0.3126 2.7293
Coefficients:
Estimate Std. Error z value Pr(>|z|)
factor(period)7 -2.9943 0.3175 -9.431 < 2e-16 ***
factor(period)8 -3.7001 0.4205 -8.800 < 2e-16 ***
factor(period)9 -2.2811 0.2724 -8.374 < 2e-16 ***
factor(period)10 -1.8226 0.2585 -7.052 1.77e-12 ***
factor(period)11 -1.6542 0.2691 -6.147 7.89e-10 ***
factor(period)12 -1.1791 0.2716 -4.341 1.42e-05 ***
pt 0.8736 0.2174 4.018 5.86e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1139.53 on 822 degrees of freedom
Residual deviance: 634.66 on 815 degrees of freedom
AIC: 648.66
Number of Fisher Scoring iterations: 5
anova(modelB)
Analysis of Deviance Table
Model: binomial, link: logit
Response: event
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev
NULL 822 1139.53
factor(period) 6 487.58 816 651.96
pt 1 17.29 815 634.66
Model C:
modelC<-glm(event~factor(period) + pas - 1, family="binomial", data=firstsex.pp)
summary(modelC)
Call:
glm(formula = event ~ factor(period) + pas - 1, family = "binomial",
data = firstsex.pp)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.1548 -0.6360 -0.4475 -0.2725 2.6829
Coefficients:
Estimate Std. Error z value Pr(>|z|)
factor(period)7 -2.4646 0.2741 -8.991 < 2e-16 ***
factor(period)8 -3.1591 0.3889 -8.123 4.55e-16 ***
factor(period)9 -1.7297 0.2245 -7.705 1.31e-14 ***
factor(period)10 -1.2851 0.2127 -6.043 1.51e-09 ***
factor(period)11 -1.1360 0.2324 -4.889 1.01e-06 ***
factor(period)12 -0.6421 0.2428 -2.644 0.008187 **
pas 0.4428 0.1140 3.886 0.000102 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1139.53 on 822 degrees of freedom
Residual deviance: 637.17 on 815 degrees of freedom
AIC: 651.17
Number of Fisher Scoring iterations: 5
anova(modelC)
Analysis of Deviance Table
Model: binomial, link: logit
Response: event
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev
NULL 822 1139.53
factor(period) 6 487.58 816 651.96
pas 1 14.79 815 637.17
Model D:
modelD<-glm(event~factor(period) + pt + pas - 1, family="binomial", data=firstsex.pp)
summary(modelD)
Call:
glm(formula = event ~ factor(period) + pt + pas - 1, family = "binomial",
data = firstsex.pp)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.1787 -0.6182 -0.4338 -0.2836 2.7862
Coefficients:
Estimate Std. Error z value Pr(>|z|)
factor(period)7 -2.8932 0.3206 -9.024 < 2e-16 ***
factor(period)8 -3.5848 0.4230 -8.474 < 2e-16 ***
factor(period)9 -2.1502 0.2775 -7.750 9.20e-15 ***
factor(period)10 -1.6932 0.2646 -6.398 1.58e-10 ***
factor(period)11 -1.5177 0.2757 -5.504 3.71e-08 ***
factor(period)12 -1.0099 0.2811 -3.592 0.000328 ***
pt 0.6605 0.2367 2.790 0.005266 **
pas 0.2964 0.1254 2.364 0.018089 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1139.53 on 822 degrees of freedom
Residual deviance: 629.15 on 814 degrees of freedom
AIC: 645.15
Number of Fisher Scoring iterations: 5
modelD<-glm(event~factor(period) + pas + pt - 1, family="binomial", data=firstsex.pp)
anova(modelD)
Analysis of Deviance Table
Model: binomial, link: logit
Response: event
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev
NULL 822 1139.53
factor(period) 6 487.58 816 651.96
pas 1 14.79 815 637.17
pt 1 8.02 814 629.15
modelD<-glm(event~factor(period) + pt + pas - 1, family="binomial", data=firstsex.pp)
anova(modelD)
Analysis of Deviance Table
Model: binomial, link: logit
Response: event
Terms added sequentially (first to last)
Df Deviance Resid. Df Resid. Dev
NULL 822 1139.53
factor(period) 6 487.58 816 651.96
pt 1 17.29 815 634.66
pas 1 5.51 814 629.15
Table 11.4, page 388
modelA<-glm(event~factor(period) - 1, family="binomial", data=firstsex.pp)
col0<-c(7:12)
col1<-c("D7", "D8", "D9", "D10", "D11", "D12")
col2<-exp(modelA$coefficients)
col3<- 1 /(1+exp(-modelA$coefficients))
tab11.4<-data.frame(time=col0, Predictor=col1, parameter=modelA$coefficients,
fitted.odds=col2, fitted.hazard=col3, row.names=NULL)
tab11.4
time Predictor parameter fitted.odds fitted.hazard 1 7 D7 -2.3978953 0.0909091 0.08333333 2 8 D8 -3.1166848 0.0443038 0.04242425 3 9 D9 -1.7197860 0.1791045 0.15189873 4 10 D10 -1.2866645 0.2761905 0.21641791 5 11 D11 -1.1631508 0.3125000 0.23809524 6 12 D12 -0.7308875 0.4814815 0.32500000
Table 11.5 on page 392 based on Model B.
modelB<-glm(event~factor(period) + pt - 1, family="binomial", data=firstsex.pp)
t<-data.frame(hazard=modelB$fitted.values, time=firstsex.pp$period, pt=firstsex.pp$pt)
t$logit<-log(t$hazard/(1-t$hazard))
ta<-aggregate(t, list(pt=t$pt, time=t$time),mean)
ta.0<-ta[ta$pt==0, ]
ta.1<-ta[ta$pt==1, ]
c1<-c(7:12)
c2<-ta.0$logit
c3<-ta.1$logit-ta.0$logit
c4<-ta.0$logit
c5<-ta.1$logit
c6<-ta.0$hazard
c7<-ta.1$hazard
tab11.5<-data.frame(time=c1, alpha=c2, beta=c3, logit_0 = c4, logit_1= c5,
hazard_0 = c6, hazard_1 = c7)
tab11.5$surv_0<-c(1:7)
tab11.5$surv_1<-c(1:7)
tab11.5$surv_0[1]<-1-tab11.5$hazard_0[1]
tab11.5$surv_1[1]<-1-tab11.5$hazard_1[1]
for(i in 2:6) {
tab11.5$surv_0[i] = tab11.5$surv_0[i-1]*(1-tab11.5$hazard_0[i])
tab11.5$surv_1[i] = tab11.5$surv_1[i-1]*(1-tab11.5$hazard_1[i])
}
tab11.5
time alpha beta logit_0 logit_1 hazard_0 hazard_1 surv_0 surv_1 1 7 -2.994327 0.8736184 -2.994327 -2.1207082 0.04768284 0.10710033 0.9523172 0.8928997 2 8 -3.700124 0.8736184 -3.700124 -2.8265055 0.02412410 0.05590856 0.9293434 0.8429789 3 9 -2.281124 0.8736184 -2.281124 -1.4075051 0.09269841 0.19662787 0.8431947 0.6772258 4 10 -1.822599 0.8736184 -1.822599 -0.9489801 0.13912236 0.27908998 0.7258875 0.4882189 5 11 -1.654227 0.8736184 -1.654227 -0.7806088 0.16053845 0.31418869 0.6093546 0.3348260 6 12 -1.179057 0.8736184 -1.179057 -0.3054385 0.23522180 0.42422854 0.4660211 0.1927833
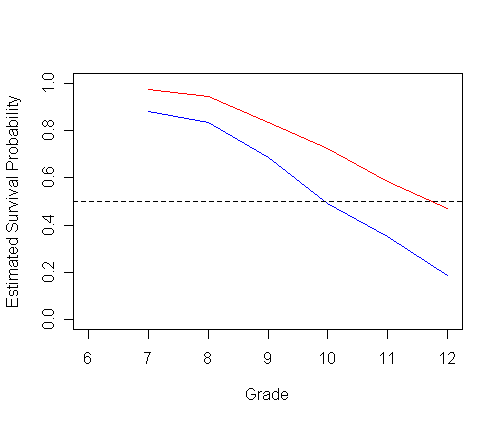
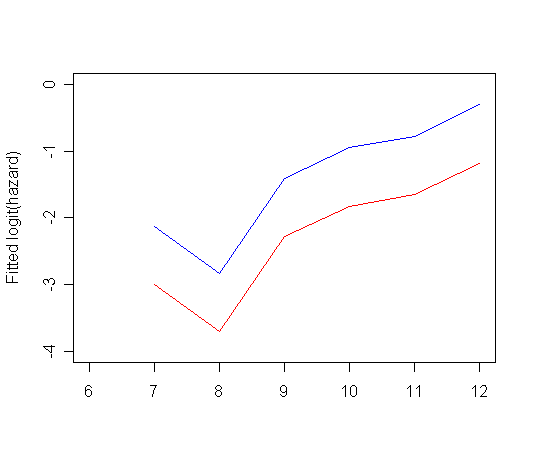
Figure 11.6, page 393 using Model B. The data for the graphs, tab11.5, has been created in previous example.
plot(tab11.5$time, tab11.5$logit_0, type="l", ylab="Fitted logit(hazard)",
ylim=c(-4, 0), xlim=c(6, 12), xlab="", col="red")
par(new=T)
plot(tab11.5$time, tab11.5$logit_1, type="l", ylab="", ylim=c(-4, 0), xlim=c(6, 12), xlab="", col="blue")
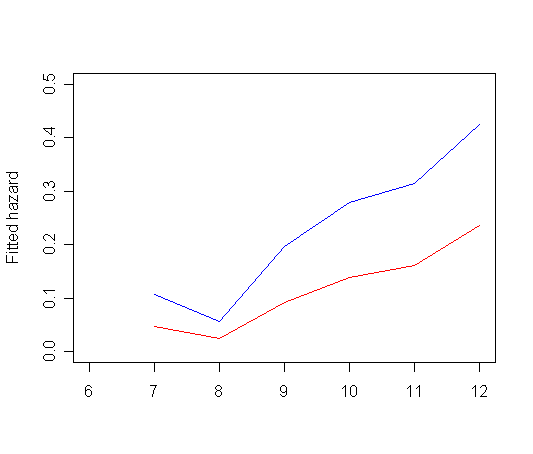
plot(tab11.5$time, tab11.5$hazard_0, type="l", ylab="Fitted hazard",
ylim=c(0, 0.5), xlim=c(6, 12), xlab="", col="red")
par(new=T)
plot(tab11.5$time, tab11.5$hazard_1, type="l", ylab="", ylim=c(0, 0.5), xlim=c(6, 12), xlab="", col="blue")
plot(tab11.5$time, tab11.5$surv_0, type="l", ylab="Fitted survival probability",
ylim=c(0, 1), xlim=c(6, 12), xlab="", col="red")
par(new=T)
plot(tab11.5$time, tab11.5$surv_1, type="l", ylab="", ylim=c(0,1), xlim=c(6, 12), xlab="", col="blue")
abline(h=c(.5), lty=2)
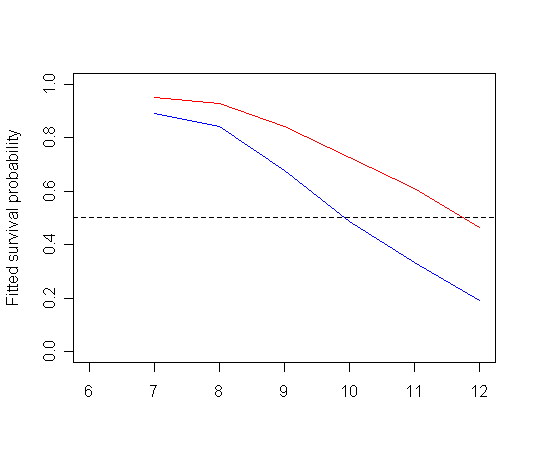
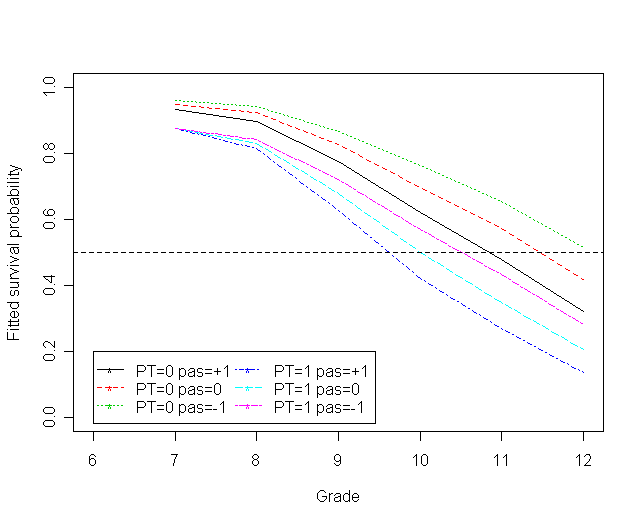
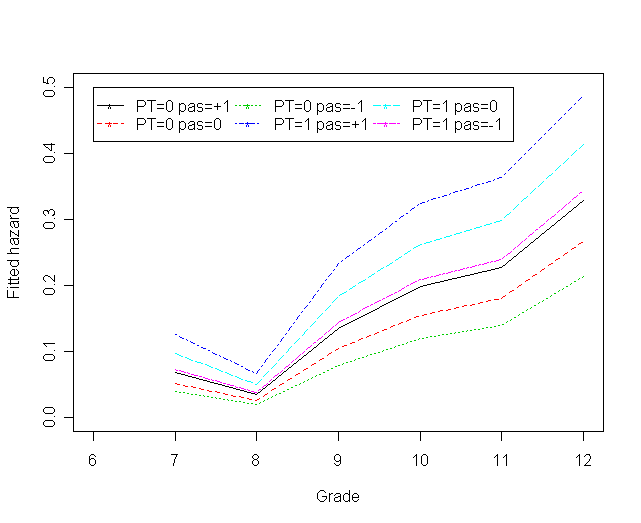
Figure 11.7 on page 395 based on Model D.
modelD<-glm(event~factor(period) + pt + pas - 1, family="binomial", data=firstsex.pp)
coeff<-data.frame(modelD$coefficients)
myt<-c(1:6)
h0_pas1<-c(1:6)
h0_pas0<-c(1:6)
h0_pasn1<-c(1:6)
h1_pas1<-c(1:6)
h1_pas0<-c(1:6)
h1_pasn1<-c(1:6)
for(i in 1:6) {
myt[i]<-i+6
h0_pas1[i]<-1/(1+ exp(-(coeff[i,] + coeff[8,])))
h0_pas0[i]<-1/(1+ exp(-coeff[i,]))
h0_pasn1[i]<-1/(1+ exp(-(coeff[i,] - coeff[8,])))
h1_pas1[i]<-1/(1+ exp(-(coeff[i,] + coeff[8,] + coeff[7,])))
h1_pas0[i]<-1/(1+ exp(-(coeff[i,] + coeff[7,])))
h1_pasn1[i]<-1/(1+ exp(-(coeff[i,] - coeff[8,] + coeff[7,])))
}
f<-cbind(h0_pas1,h0_pas0,h0_pasn1, h1_pas1,h1_pas0,h1_pasn1)
matplot(myt, f, type="l", ylab="Fitted hazard", ylim=c(0, 0.5), xlim=c(6, 12),
xlab="Grade", col=1:6, lty=1:6)
legend(6, .5, c("PT=0 pas=+1", "PT=0 pas=0", "PT=0 pas=-1",
"PT=1 pas=+1", "PT=1 pas=0", "PT=1 pas=-1"),
col=1:6, lty=1:6, pch = "*",
ncol =3, cex = 1)
surv0_pas1<-c(1:6)
surv0_pas0<-c(1:6)
surv0_pasn1<-c(1:6)
surv1_pas1<-c(1:6)
surv1_pas0<-c(1:6)
surv1_pasn1<-c(1:6)
surv0_pas1[1]<-1-h0_pas1[1]
surv0_pas0<-1-h0_pas0[1]
surv0_pasn1<-1-h0_pasn1[1]
surv1_pas1<-1-h1_pas1[1]
surv1_pas0<-1-h1_pas1[1]
surv1_pasn1<-1-h1_pas1[1]
for(i in 2:6) {
surv0_pas1[i] = surv0_pas1[i-1]*(1-h0_pas1[i])
surv0_pas0[i] = surv0_pas0[i-1]*(1-h0_pas0[i])
surv0_pasn1[i] = surv0_pasn1[i-1]*(1-h0_pasn1[i])
surv1_pas1[i] = surv1_pas1[i-1]*(1-h1_pas1[i])
surv1_pas0[i] = surv1_pas0[i-1]*(1-h1_pas0[i])
surv1_pasn1[i] = surv1_pasn1[i-1]*(1-h1_pasn1[i])
}
s<-cbind(surv0_pas1,surv0_pas0,surv0_pasn1,surv1_pas1,surv1_pas0,surv1_pasn1)
matplot(myt, s, type="l", ylab="Fitted survival probability", ylim=c(0, 1), xlim=c(6, 12),
xlab="Grade", col=1:6, lty=1:6)
abline(h=c(.5), lty=2)
legend(6, .2, c("PT=0 pas=+1", "PT=0 pas=0", "PT=0 pas=-1",
"PT=1 pas=+1", "PT=1 pas=0", "PT=1 pas=-1"),
col=1:6, lty=1:6, pch = "*",
ncol =2, cex = 1)
