R Textbook Examples Applied Longitudinal Data Analysis: Modeling Change and Event Occurrence by Judith D. Singer and John B. Willett Chapter 14: Fitting Cox Regression Models
The examples on the page were written in R version 2.4.1.
This page requires the R package survival.
library(survival)
Figure 14.1, page 505. To generate this set of plots, we first separated our data into two datasets, grouped on personal. Next, we ran an empty Cox model and, using the survfit function, we generated the event times and estimated survival probabilities at the event times for both datasets. These probabilities are plotted, using a step function, in the first graph. The second graph shows the corresponding cumulative hazard. We calculated this by taking the negative log of the survival probabilities.
rearrest<-read.table("https://stats.idre.ucla.edu/stat/examples/alda/rearrest.csv", sep=",", header=T) rearrest0 <- subset(rearrest, personal == 0) rearrest1 <- subset(rearrest, personal == 1) f14.1.0 <- summary(survfit(Surv(rearrest0$months, abs(rearrest0$censor - 1))~1)) f14.1.1 <- summary(survfit(Surv(rearrest1$months, abs(rearrest1$censor - 1))~1)) s.hat.0 <- f14.1.0$surv time.0 <- f14.1.0$time s.hat.1 <- f14.1.1$surv time.1 <- f14.1.1$time s.hat.steps.0 <- stepfun(time.0, c(1, s.hat.0)) s.hat.steps.1 <- stepfun(time.1, c(1, s.hat.1)) plot(s.hat.steps.0, do.points = FALSE, xlim = c(0, 36), ylim = c(0,1), ylab = "Estimated Survival", xlab = "Months after release", main = "") lines(s.hat.steps.1, do.points = FALSE, xlim = c(0,36), lty = 2) legend("bottomleft", c("Personal = 0", "Personal = 1"), lty = c(1, 2))h.hat.0 <- -log(s.hat.0) h.hat.1 <- -log(s.hat.1) h.hat.steps.0 <- stepfun(time.0, c(0, h.hat.0)) h.hat.steps.1 <- stepfun(time.1, c(0, h.hat.1)) plot(h.hat.steps.0, do.points = FALSE, xlim = c(0, 36), ylim = c(0,1.4), ylab = "Estimated Cumulative Hazard", xlab = "Months after release", main = "") lines(h.hat.steps.1, do.points = FALSE, xlim = c(0,36), lty = 2) legend("bottomright", c("Personal = 0", "Personal = 1"), lty = c(1, 2))
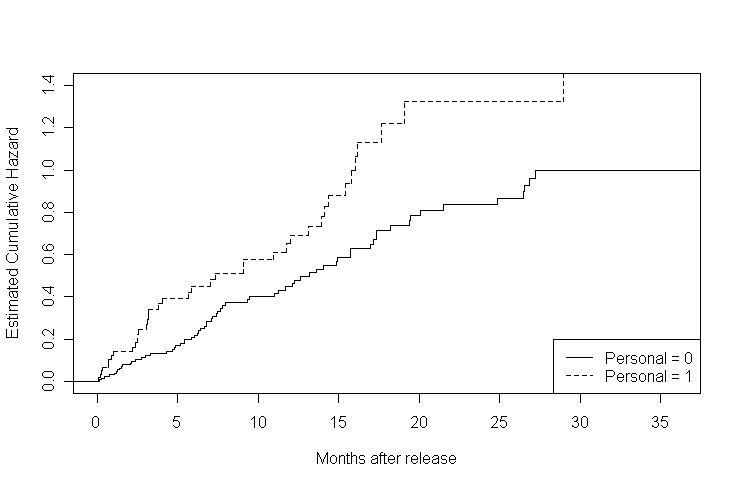
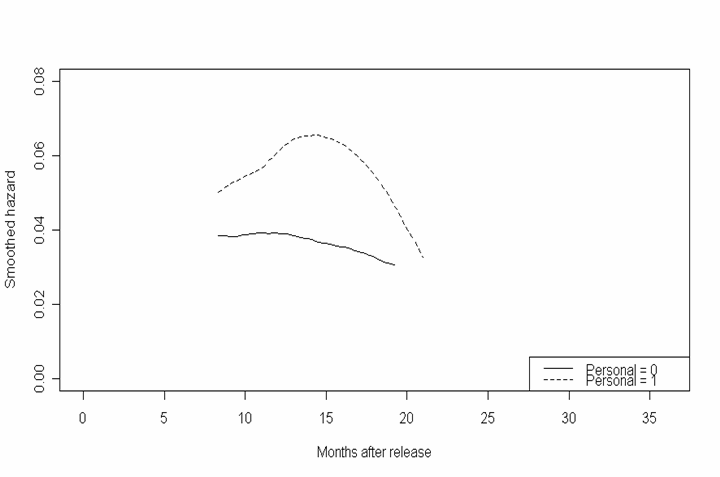
We generated the third graph by first writing a function smooth that takes the time and estimated survival probabilities from survfit and aggregates the hazard over a given width of time.
This function was written using the same smoothing algorithm the authors used. If we were to use one of R’s kernel smoothing functions (like ksmooth), we would not be able to exactly reproduce the graphs as they appear in the text. In this instance, the bandwidth of the graph in the text appears to be 8.
smooth<- function(width, time, survive){
n=length(time)
lo=time[1] + width
hi=time[n] - width
npt=50
inc=(hi-lo)/npt
s=lo+t(c(1:npt))*inc
slag = c(1, survive[1:n-1])
h=1-survive/slag
x1 = as.vector(rep(1, npt))%*%(t(time))
x2 = t(s)%*%as.vector(rep(1,n))
x = (x1 - x2) / width
k=.75*(1-x*x)*(abs(x)<=1)
lambda=(k%*%h)/width
smoothed= list(x = s, y = lambda)
return(smoothed)
}
bw1.0 <- smooth(8, time.0, s.hat.0)
bw1.1 <- smooth(8, time.1, s.hat.1)
plot(bw1.0$x, bw1.0$y, type = "l", xlim = c(0, 36), ylim = c(0, .08), xlab = "Months after release", ylab = "Smoothed hazard")
points(bw1.1$x, bw1.1$y, type = "l", lty = 2)
legend("bottomright", c("Personal = 0", "Personal = 1"), lty = c(1, 2))
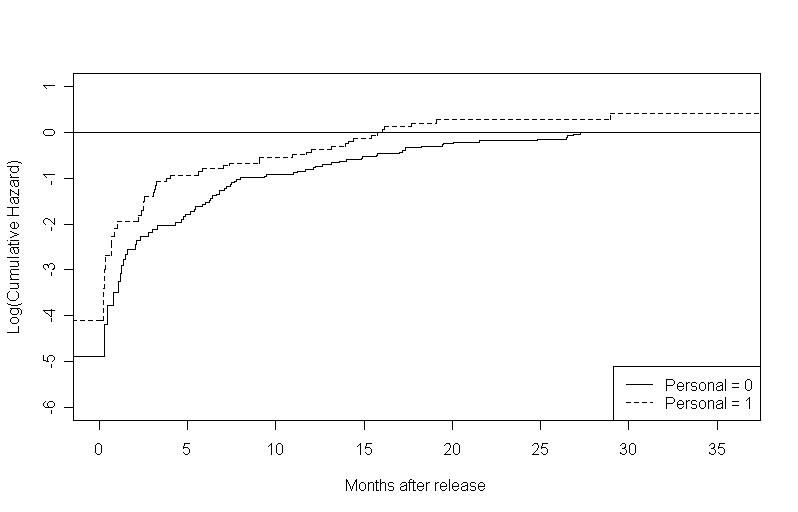
Figure 14.2, page 508. To generate the first in this set of graphs, we created a step function from the log of the cumulative hazard calculated in the previous example.
l.hat.0 <- log(h.hat.0) l.hat.1 <- log(h.hat.1) log.h.steps.0<- stepfun(time.0, c(l.hat.0[1], l.hat.0)) log.h.steps.1<- stepfun(time.1, c(l.hat.1[1], l.hat.1)) par(mfrow=c(1,1)) plot(log.h.steps.0, do.points = FALSE, xlim = c(0, 36), ylim = c(-6.0,1), ylab = "Log(Cumulative Hazard)", xlab = "Months after release", main = "") lines(log.h.steps.1, do.points = FALSE, xlim = c(0,36), lty = 2) points(c(-5, 36), c(0,0), type = "l") legend("bottomright", c("Personal = 0", "Personal = 1"), lty = c(1, 2))
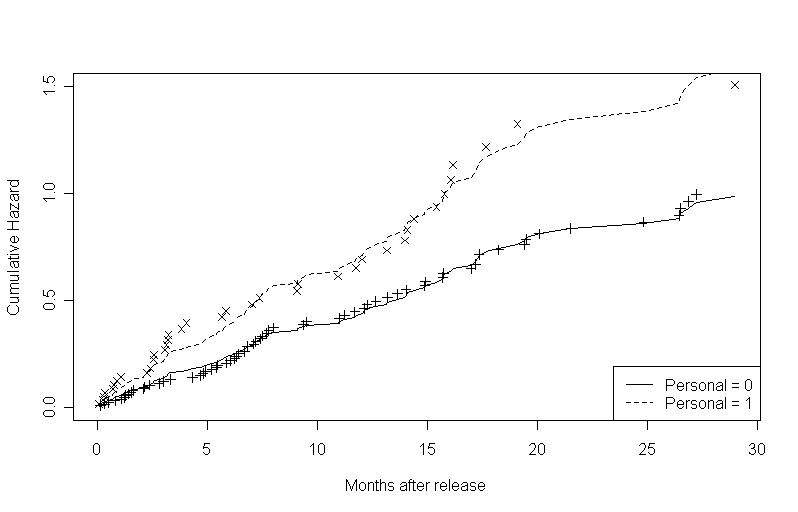
To generate the second and third graphs in this set, we first ran a Cox model with personal as a predictor. We then created one data frame where personal is 0 and one data frame where personal is 1 and used the model to obtain estimates of the hazard rate for each value of personal (using the proportional hazards assumption). We then plotted the fitted curves from the model and overlaid the non-parametric estimates for the log cumulative hazard at the times of events on the second graph. The third graph is based on the cumulative hazard rather than the log cumulative hazard.
attach(rearrest)f14.2 <- coxph(Surv(months, abs(censor - 1))~personal, method = "efron") personal.0 <- data.frame(personal=0) personal.1 <- data.frame(personal=1) s.base <- survfit(f14.2, newdata = personal.0, type = "kaplan-meier") s.personal <- survfit(f14.2, newdata = personal.1, type = "kaplan-meier") h.base <- -log(s.base$surv) h.personal <- -log(s.personal$surv) l.h.base <- log(h.base) l.h.personal <- log(h.personal) plot(s.base$time, l.h.base, type = "l", lty = 1, ylim = c(-6, 1), xlab = "Months after release", ylab = "Cumulative Hazard") points(s.personal$time, l.h.personal, type = "l", lty = 2) points(time.0, l.hat.0, pch = 3) points(time.1, l.hat.1, pch = 4) legend("bottomright", c("Personal = 0", "Personal = 1"), lty = c(1, 2))plot(s.base$time, h.base, type = "l", lty = 1, ylim = c(0,1.5), xlab = "Months after release", ylab = "Cumulative Hazard") points(s.personal$time, h.personal, type = "l", lty = 2) points(time.0, h.hat.0, pch = 3) points(time.1, h.hat.1, pch = 4) legend("bottomright", c("Personal = 0", "Personal = 1"), lty = c(1, 2))
Table 14.1, page 525. To generate the parameter estimates and model statistics seen in this table, we ran Cox models with the predictors specified in the table.
tab14.1A <- coxph(Surv(months, abs(censor - 1))~personal) summary(tab14.1A) coef exp(coef) se(coef) z p personal 0.479 1.61 0.202 2.36 0.018 exp(coef) exp(-coef) lower .95 upper .95 personal 1.61 0.62 1.09 2.4 Rsquare= 0.027 (max possible= 0.994 ) Likelihood ratio test= 5.32 on 1 df, p=0.0210 Wald test = 5.59 on 1 df, p=0.0181 Score (logrank) test = 5.69 on 1 df, p=0.017 tab14.1B <- coxph(Surv(months, abs(censor - 1))~property) summary(tab14.1B) coef exp(coef) se(coef) z p property 1.19 3.3 0.349 3.42 0.00063 exp(coef) exp(-coef) lower .95 upper .95 property 3.3 0.303 1.67 6.55 Rsquare= 0.08 (max possible= 0.994 ) Likelihood ratio test= 16.2 on 1 df, p=5.68e-05 Wald test = 11.7 on 1 df, p=0.000626 Score (logrank) test = 13.1 on 1 df, p=0.000290 tab14.1C <- coxph(Surv(months, abs(censor - 1))~cage) summary(tab14.1C) coef exp(coef) se(coef) z p cage -0.0681 0.934 0.0156 -4.36 1.3e-05 exp(coef) exp(-coef) lower .95 upper .95 cage 0.934 1.07 0.906 0.963 Rsquare= 0.112 (max possible= 0.994 ) Likelihood ratio test= 23.0 on 1 df, p=1.65e-06 Wald test = 19 on 1 df, p=1.31e-05 Score (logrank) test = 19.2 on 1 df, p=1.19e-05 tab14.1D <- coxph(Surv(months, abs(censor - 1))~personal + property + cage) summary(tab14.1D) coef exp(coef) se(coef) z p personal 0.5691 1.767 0.2052 2.77 0.00550 property 0.9358 2.549 0.3509 2.67 0.00770 cage -0.0667 0.935 0.0168 -3.98 0.00007 exp(coef) exp(-coef) lower .95 upper .95 personal 1.767 0.566 1.182 2.641 property 2.549 0.392 1.282 5.071 cage 0.935 1.069 0.905 0.967 Rsquare= 0.182 (max possible= 0.994 ) Likelihood ratio test= 39.0 on 3 df, p=1.77e-08 Wald test = 29 on 3 df, p=2.21e-06 Score (logrank) test = 30.3 on 3 df, p=1.20e-06
Table 14.2, page 533. To generate this table, we wrote a function risk.score that takes an ID as an argument and returns a vector containing the information for the given ID (including the risk score). We then called this function for the set of IDs that appear in the table and combined the vectors of information from each function call into a table.
risk.score <- function(ID.num){
temp <- subset(rearrest, id==ID.num)
log.score <- tab14.1D$coef[1]*temp$personal + tab14.1D$coef[2]*temp$property + tab14.1D$coef[3]*temp$cage
score <- exp(log.score)
day <- temp$months * (365/12)
table.row <- cbind(temp$id, temp$personal, temp$property, temp$cage, score, day, temp$months, temp$censor)
colnames(table.row) <- c("ID", "personal", "property", "centered.age", "risk.score", "day", "months", "censor")
rownames(table.row) <- c()
return(table.row)
}
tab.14.2 <- rbind(
risk.score(22),
risk.score(8),
risk.score(187),
risk.score(26),
risk.score(5),
risk.score(130),
risk.score(106),
risk.score(33))
tab.14.2
ID personal property centered.age risk.score day months censor
[1,] 22 0 0 0.2577249 0.9829532 51.96441 1.7084189 1
[2,] 8 1 1 22.4507434 1.0071815 18.98700 0.6242300 1
[3,] 187 1 0 -7.2001806 2.8561843 1095.00000 36.0000000 1
[4,] 26 0 1 -7.3014811 4.1491205 71.95072 2.3655031 0
[5,] 5 1 1 -7.1645886 7.2637815 8.99384 0.2956879 0
[6,] 130 0 1 22.3905107 0.5723740 485.66735 15.9671458 1
[7,] 106 0 0 16.2029679 0.3392704 355.75633 11.6960986 0
[8,] 33 1 0 27.0612841 0.2904806 84.94182 2.7926078 1
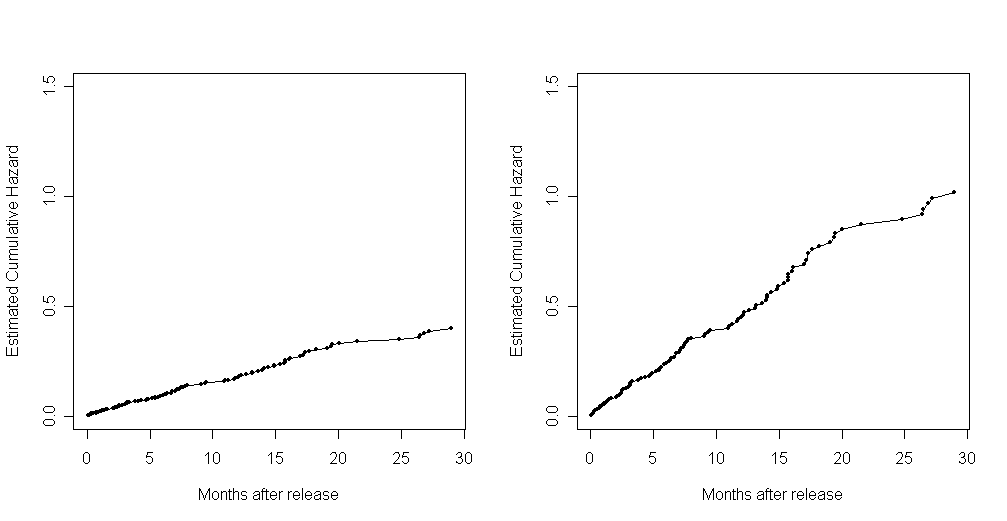
Figure 14.4, page 538. To generate these plots, we first reran the fourth model from table 14.1 and created two data frames: one representing the baseline (all predictors equal to zero) and one representing the average (all predictors equal to their sample means). We then used the model to predict survival and cumulative hazard rates for both the baseline and average case and plotted the results in the first four graphs. For the fifth and sixth graphs, we again used the smooth function described earlier in this page to generate kernel smoothed values of the hazard function.
tab14.1D <- coxph(Surv(months, abs(censor - 1))~personal + property + cage) base <- data.frame(personal=0, property=0, cage=0) ss <- survfit(tab14.1D) ss.base <- survfit(tab14.1D, newdata = base) avg <- data.frame(personal=mean(personal), property=mean(property), cage=0) ss.avg <- survfit(tab14.1D, newdata = avg) par(mfrow=c(1,2)) plot(ss.base$time, ss.base$surv, type = "l", ylim = c(0,1), xlab = "Months after release", ylab = "Estimated Survival") points(ss.base$time, ss.base$surv, pch = 20) plot(ss.avg$time, ss.avg$surv, type = "l", ylim = c(0,1), xlab = "Months after release", ylab = "Estimated Survival") points(ss.avg$time, ss.avg$surv, pch = 20)plot(ss.base$time, -log(ss.base$surv), type = "l", ylim = c(0,1.5), xlab = "Months after release", ylab = "Estimated Cumulative Hazard") points(ss.base$time, -log(ss.base$surv), pch = 20) plot(ss.avg$time, -log(ss.avg$surv), type = "l", ylim = c(0,1.5), xlab = "Months after release", ylab = "Estimated Cumulative Hazard") points(ss.avg$time, -log(ss.avg$surv), pch = 20)
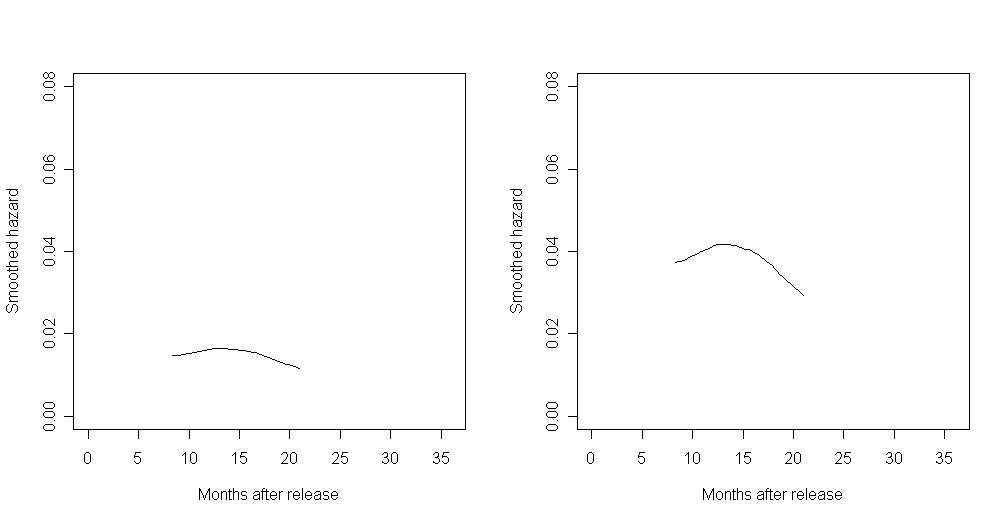
smooth.base <- smooth(8, ss.base$time, ss.base$surv) smooth.avg<- smooth(8, ss.avg$time, ss.avg$surv) plot(smooth.base$x, smooth.base$y, type = "l", xlim = c(0, 36), ylim = c(0, .08), xlab = "Months after release", ylab = "Smoothed hazard") plot(smooth.avg$x, smooth.avg$y, type = "l", xlim = c(0, 36), ylim = c(0, .08), xlab = "Months after release", ylab = "Smoothed hazard")
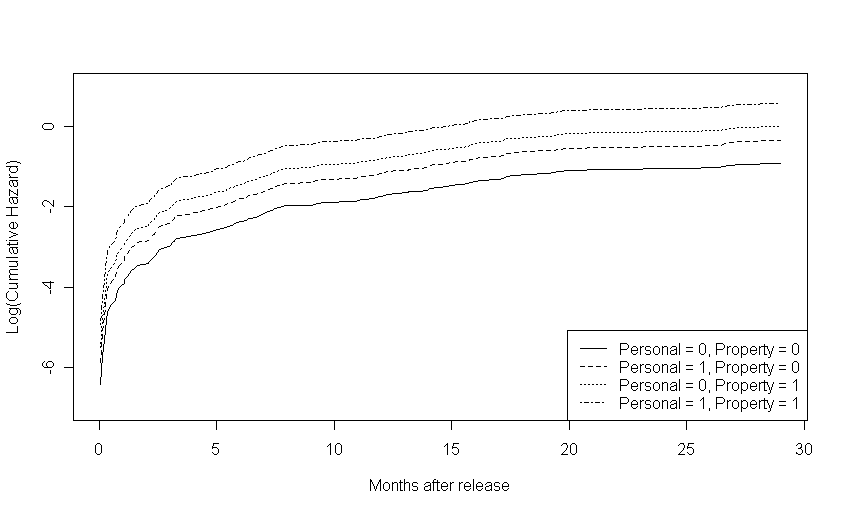
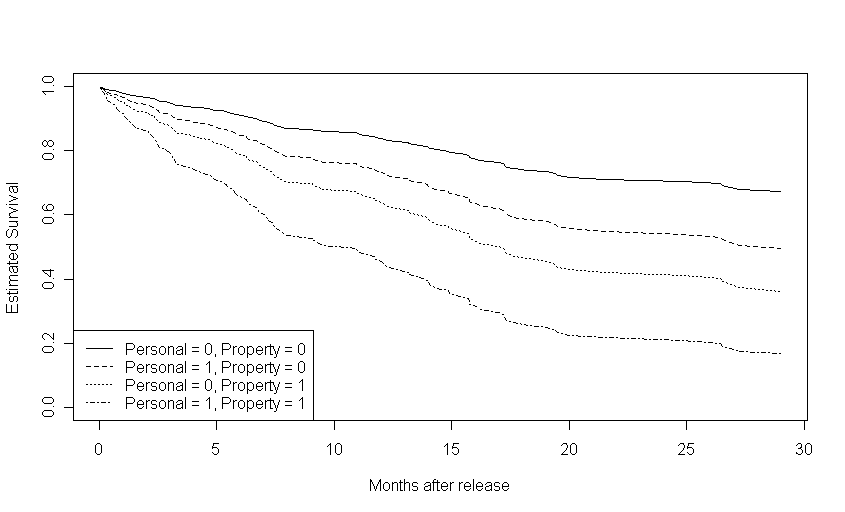
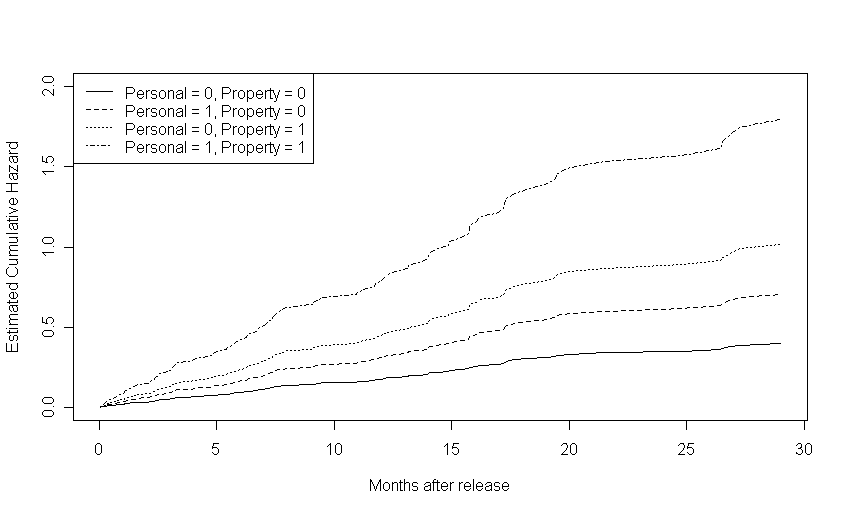
Figure 14.5, page 541.To generate these plots, we first reran the fourth model from table 14.1 and created four data frames, all with age variable set to its mean (zero, since age is centered). One data frame had personal and property values both set to 0, one data frame had personal set to 1 and property to 0, one data frame had property set to 1 and personal set to 0, and the fourth data frame had both personal and property set to zero. We then used the model to predict survival (first graph), cumulative hazard (second graph), and log cumulative hazard (third graph) for each of the four scenarios represented in a data frame and plotted each set of estimates.
tab14.1D <- coxph(Surv(months, abs(censor - 1))~personal + property + cage)
base <- data.frame(personal=0, property=0, cage=0)
personal.only <- data.frame(personal=1, property=0, cage=0)
property.only <- data.frame(personal=0, property=1, cage=0)
both <- data.frame(personal=1, property=1, cage=0)
s.base <- survfit(tab14.1D, newdata = base)
s.personal <- survfit(tab14.1D, newdata = personal.only)
s.property <- survfit(tab14.1D, newdata = property.only)
s.both <- survfit(tab14.1D, newdata = both)
par(mfrow=c(1,1))
plot(s.base$time, s.base$surv, type = "l", lty = 1, ylim = c(0,1), xlab = "Months after release", ylab = "Estimated Survival")
points(s.personal$time, s.personal$surv, type = "l", lty = 2)
points(s.property$time, s.property$surv, type = "l", lty = 3)
points(s.both$time, s.both$surv, type = "l", lty = 4)
legend("bottomleft", c("Personal = 0, Property = 0", "Personal = 1, Property = 0", "Personal = 0, Property = 1", "Personal = 1, Property = 1"), lty = c(1, 2, 3, 4))
h.base <- -log(s.base$surv)
h.personal <- -log(s.personal$surv)
h.property <- -log(s.property$surv)
h.both <- -log(s.both$surv)
plot(s.base$time, h.base, type = "l", lty = 1, ylim = c(0,2), xlab = "Months after release", ylab = "Estimated Cumulative Hazard")
points(s.personal$time, h.personal, type = "l", lty = 2)
points(s.property$time, h.property, type = "l", lty = 3)
points(s.both$time, h.both, type = "l", lty = 4)
legend("topleft", c("Personal = 0, Property = 0", "Personal = 1, Property = 0", "Personal = 0, Property = 1", "Personal = 1, Property = 1"), lty = c(1, 2, 3, 4))
l.h.base <- log(h.base)
l.h.personal <- log(h.personal)
l.h.property <- log(h.property)
l.h.both <- log(h.both)
plot(s.base$time, l.h.base, type = "l", lty = 1, ylim = c(-7,1), xlab = "Months after release", ylab = "Log(Cumulative Hazard)")
points(s.personal$time, l.h.personal, type = "l", lty = 2)
points(s.property$time, l.h.property, type = "l", lty = 3)
points(s.both$time, l.h.both, type = "l", lty = 4)
legend("bottomright", c("Personal = 0, Property = 0", "Personal = 1, Property = 0", "Personal = 0, Property = 1", "Personal = 1, Property = 1"), lty = c(1, 2, 3, 4))
