R Textbook Examples Applied Longitudinal Data Analysis: Modeling Change and Event Occurrence by Judith D. Singer and John B. Willett Chapter 2: Exploring Longitudinal Data on Change
The comma separated text files linked on the main page have capitalized variable names. On this page the variable names are all lower case. For the appropriate lower case versions use tolerance1.txt and tolerance1_pp.txt.
Fig. 2.1, p. 18.
Inputting and printing the tolerance “person-level” data
tolerance <- read.table("https://stats.idre.ucla.edu/wp-content/uploads/2016/02/tolerance1.txt", sep=",", header=T)
print(tolerance)
id tol11 tol12 tol13 tol14 tol15 male exposure
1 9 2.23 1.79 1.90 2.12 2.66 0 1.54
2 45 1.12 1.45 1.45 1.45 1.99 1 1.16
3 268 1.45 1.34 1.99 1.79 1.34 1 0.90
4 314 1.22 1.22 1.55 1.12 1.12 0 0.81
5 442 1.45 1.99 1.45 1.67 1.90 0 1.13
6 514 1.34 1.67 2.23 2.12 2.44 1 0.90
7 569 1.79 1.90 1.90 1.99 1.99 0 1.99
8 624 1.12 1.12 1.22 1.12 1.22 1 0.98
9 723 1.22 1.34 1.12 1.00 1.12 0 0.81
10 918 1.00 1.00 1.22 1.99 1.22 0 1.21
11 949 1.99 1.55 1.12 1.45 1.55 1 0.93
12 978 1.22 1.34 2.12 3.46 3.32 1 1.59
13 1105 1.34 1.90 1.99 1.90 2.12 1 1.38
14 1542 1.22 1.22 1.99 1.79 2.12 0 1.44
15 1552 1.00 1.12 2.23 1.55 1.55 0 1.04
16 1653 1.11 1.11 1.34 1.55 2.12 0 1.25
Inputting and printing the tolerance “person-level” data
tolerance.pp <- read.table("https://stats.idre.ucla.edu/wp-content/uploads/2016/02/tolerance1_pp.txt", sep=",", header=T)
attach(tolerance.pp)
print(tolerance.pp[c(1:9, 76:80), ])
id age tolerance male exposure time
1 9 11 2.23 0 1.54 0
2 9 12 1.79 0 1.54 1
3 9 13 1.90 0 1.54 2
4 9 14 2.12 0 1.54 3
5 9 15 2.66 0 1.54 4
6 45 11 1.12 1 1.16 0
7 45 12 1.45 1 1.16 1
8 45 13 1.45 1 1.16 2
9 45 14 1.45 1 1.16 3
76 1653 11 1.11 0 1.25 0
77 1653 12 1.11 0 1.25 1
78 1653 13 1.34 0 1.25 2
79 1653 14 1.55 0 1.25 3
80 1653 15 2.12 0 1.25 4
Table 2.1, p. 20. Bivariate correlation among tolerance scores assessed on five occassions.
cor(tolerance[ , 2:6])
tol11 tol12 tol13 tol14 tol15
tol11 1.00000000 0.6572937 0.06194915 0.1407631 0.2635371
tol12 0.65729370 1.0000000 0.24755116 0.2056198 0.3922781
tol13 0.06194915 0.2475512 1.00000000 0.5871742 0.5692116
tol14 0.14076312 0.2056198 0.58717422 1.0000000 0.8254566
tol15 0.26353705 0.3922781 0.56921163 0.8254566 1.0000000
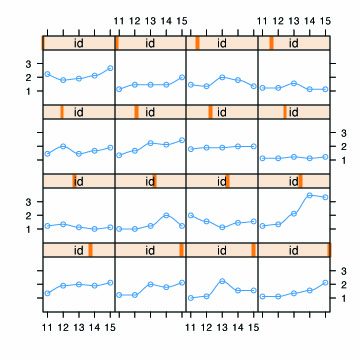
Fig. 2.2, p. 25. Empirical growth plots.
library(lattice) # load lattice library for xyplot function xyplot(tolerance ~ age | id, data=tolerance.pp, as.table=T)
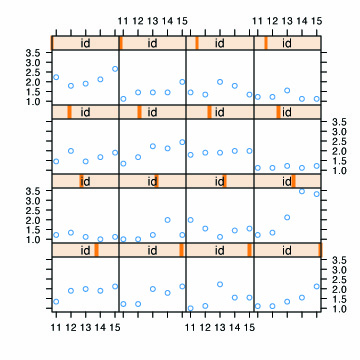
Fig. 2.3, p. 27. Smooth nonparametric trajectories superimposed on empirical growth plots.
xyplot(tolerance~age | id, data=tolerance.pp,
prepanel = function(x, y) prepanel.loess(x, y, family="gaussian"),
xlab = "Age", ylab = "Tolerance",
panel = function(x, y) {
panel.xyplot(x, y)
panel.loess(x,y, family="gaussian") },
ylim=c(0, 4), as.table=T)
Table 2.2, p. 30. Fitting separate within person OLS regression models.
by(tolerance.pp, id, function(x) summary(lm(tolerance ~ time, data=x)))
tolerance.pp$id: 9
Call:
lm(formula = tolerance ~ time, data = x)
Residuals:
1 2 3 4 5
0.328 -0.231 -0.240 -0.139 0.282
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.9020 0.2519 7.549 0.00482 **
time 0.1190 0.1029 1.157 0.33105
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.3253 on 3 degrees of freedom
Multiple R-Squared: 0.3085, Adjusted R-squared: 0.07802
F-statistic: 1.339 on 1 and 3 DF, p-value: 0.3311
------------------------------------------------------------------------------
<some output omitted>
------------------------------------------------------------------------------
tolerance.pp$id: 1653
Call:
lm(formula = tolerance ~ time, data = x)
Residuals:
76 77 78 79 80
0.156 -0.090 -0.106 -0.142 0.182
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.95400 0.13926 6.851 0.00637 **
time 0.24600 0.05685 4.327 0.02276 *
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.1798 on 3 degrees of freedom
Multiple R-Squared: 0.8619, Adjusted R-squared: 0.8159
F-statistic: 18.72 on 1 and 3 DF, p-value: 0.02276
Fig. 2.4, p. 31.
# stem plot for the intercepts
int <- by(tolerance.pp, id, function(data)
coefficients(lm(tolerance ~ time, data = data))[[1]])
int <- unlist(int)
names(int) <- NULL
summary(int)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.954 1.138 1.287 1.358 1.547 1.902
stem(int, scale=2)
Decimal point is 1 place to the left of the colon
9 : 5
10 : 03
11 : 2489
12 : 7
13 : 1
14 : 3
15 : 448
16 :
17 : 3
18 : 2
19 : 0
# stem plot for fitted rate of change
rate <- by(tolerance.pp, id, function(data)
coefficients(lm(tolerance ~ time, data = data))[[2]])
rate <- unlist(rate)
names(rate) <- NULL
summary(rate)
Min. 1st Qu. Median Mean 3rd Qu. Max.
-0.09800 0.02225 0.13100 0.13080 0.18980 0.63200
stem(rate, scale=2)
Decimal point is 1 place to the left of the colon
-1 | 0
-0 | 53
0 | 2256
1 | 24567
2 | 457
3 |
4 |
5 |
6 | 3
# stem plot for R sq
rsq <- by(tolerance.pp, id, function(data)
summary(lm(tolerance ~ time, data = data))$r.squared)
rsq <- unlist(rsq)
names(rsq) <- NULL
summary(rsq)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.01537 0.25050 0.39170 0.49100 0.79710 0.88640
stem(rsq, scale=2)
Decimal point is 1 place to the left of the colon
0 : 27
1 : 3
2 : 55
3 : 113
4 : 5
5 :
6 : 8
7 : 78
8 : 6889
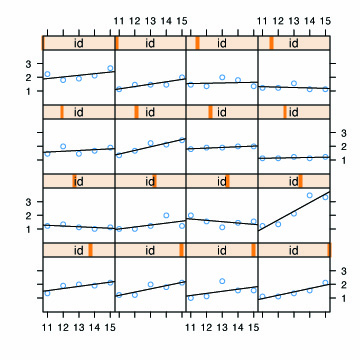
Fig. 2.5, p. 32. Fitted OLS trajectories superimposed on the empirical growth plots.
xyplot(tolerance ~ age | id, data=tolerance.pp,
panel = function(x, y){
panel.xyplot(x, y)
panel.lmline(x, y)
}, ylim=c(0, 4), as.table=T)
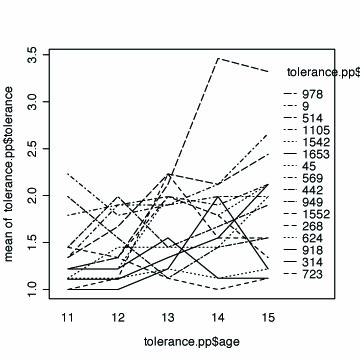
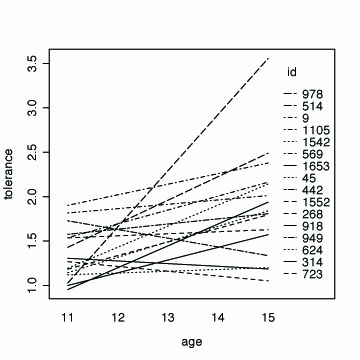
Fig. 2.6, p. 34. The collection of the trajectories of the raw data in the top panel; in the bottom panel is the collection of fitted OLS trajectories.
#plot of the raw data interaction.plot(tolerance.pp$age, tolerance.pp$id, tolerance.pp$tolerance)
# fitting the linear model by id fit <- by(tolerance.pp, id, function(bydata) fitted.values(lm(tolerance ~ time, data=bydata))) fit <- unlist(fit) # plotting the linear fit by id interaction.plot(age, id, fit, xlab="age", ylab="tolerance")
Table 2.3, p. 37 Descriptive statistics of the estimates obtained by fitting the linear model by id.
#obtaining the intercepts from linear model by id
ints <- by(tolerance.pp, tolerance.pp$id,
function(data) coefficients(lm(tolerance ~ time, data=data))[[1]])
ints1 <- unlist(ints)
names(ints1) <- NULL
mean(ints1)
[1] 1.35775
sqrt(var(ints1))
[1] 0.2977792
#obtaining the slopes from linear model by id
slopes <- by(tolerance.pp, tolerance.pp$id,
function(data) coefficients(lm(tolerance ~ time, data=data))[[2]])
slopes1 <- unlist(slopes)
names(slopes1) <- NULL
mean(slopes1)
[1] 0.1308125
sqrt(var(slopes1))
[1] 0.172296
cor( ints1, slopes1)
[1] -0.4481135
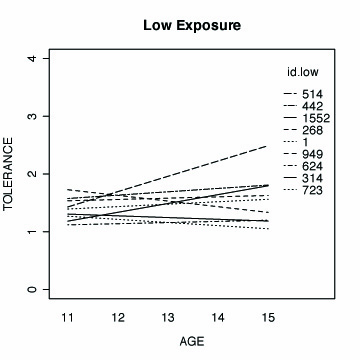
Fig. 2.7, 38 OLS fitted trajectories separated by levels of selected predictors. The two first panels are separated by gender; the two last are separated by levels of exposure.
# fitting the linear model by id, males only tolm <- tolerance.pp[male == 1 , ] fitmlist <- by(tolm, tolm$id, function(bydata) fitted.values(lm(tolerance ~ time, data=bydata))) fitm <- unlist(fitmlist) #appending the average for the whole group lm.m <- fitted( lm(tolerance ~ time, data=tolm) ) names(lm.m) <- NULL fit.m2 <- c(fitm, lm.m[1:5]) age.m <- c(tolm$age, seq(11,15)) id.m <- c(tolm$id, rep(111, 5)) #plotting the linear fit by id, males #id.m=111 denotes the average value for males interaction.plot(age.m, id.m, fit.m2, ylim=c(0, 4), xlab="AGE", ylab="TOLERANCE", lwd=1) title(main="Males")
#fitting the linear model by id, females only tol.pp.fm <- tolerance.pp[tolerance.pp$male == 0, ] fit.fm <- by(tol.pp.fm, tol.pp.fm$id, function(data) fitted.values(lm(tolerance ~ time, data=data))) fit.fm1 <- unlist(fit.fm) names(fit.fm1) <- NULL #appending the average for the whole group lm.fm <- fitted( lm(tolerance ~ time, data=tol.pp.fm) ) names(lm.fm) <- NULL fit.fm2 <- c(fit.fm1, lm.fm[1:5]) age.fm <- c(tol.pp.fm$age, seq(11,15)) id.fm <- c(tol.pp.fm$id, rep(1111, 5)) #plotting the linear fit by id, females #id.fm=1111 denotes the average for females interaction.plot(age.fm, id.fm, fit.fm2, ylim=c(0, 4), xlab="AGE", ylab="TOLERANCE", lwd=1) title(main="Females")
#We can include both plot in the same graph windows.options(width = 12, height = 5) par(mfrow = c(1, 2), mar = c(4, 4, 2, 1)) interaction.plot(age.m, id.m, fit.m2, ylim=c(0, 4), xlab="AGE", ylab="TOLERANCE", lwd=1) title(main="Males") interaction.plot(age.fm, id.fm, fit.fm2, ylim=c(0, 4), xlab="AGE", ylab="TOLERANCE", lwd=1) title(main="Females")
windows.options(reset = TRUE)
#fitting the linear model by id, low exposure
tol.pp.low <- tolerance.pp[tolerance.pp$exposure < 1.145 , ]
fit.low <- by(tol.pp.low, tol.pp.low$id,
function(data) fitted.values(lm(tolerance ~ time, data=data)))
fit.low1 <- unlist(fit.low)
names(fit.low1) <- NULL
#appending the average for the whole group
lm.low <- fitted( lm(tolerance ~ time, data=tol.pp.low) )
names(lm.low) <- NULL
fit.low2 <- c(fit.low1, lm.low[1:5])
age.low <- c(tol.pp.low$age, seq(11,15))
id.low <- c(tol.pp.low$id, rep(1, 5))
#plotting the linear fit by id, low Exposure
#id.low=1 denotes the average for group
interaction.plot(age.low, id.low, fit.low2, ylim=c(0, 4), xlab="AGE", ylab="TOLERANCE", lwd=1)
title(main="Low Exposure")
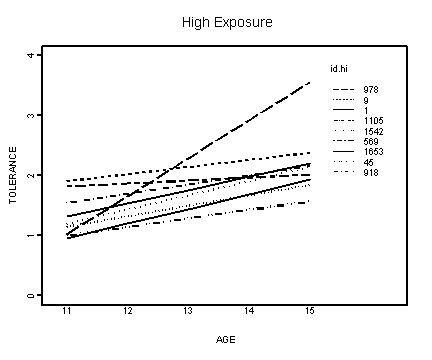
#fitting the linear model by id, high exposure
tol.pp.hi <- tolerance.pp[tolerance.pp$exposure >= 1.145 , ]
fit.hi <- by(tol.pp.hi, tol.pp.hi$id,
function(data) fitted.values(lm(tolerance ~ time, data=data)))
fit.hi1 <- unlist(fit.hi)
names(fit.hi1) <- NULL
#appending the average for the whole group
lm.hi <- fitted( lm(tolerance ~ time, data=tol.pp.hi) )
names(lm.hi) <- NULL
fit.hi2 <- c(fit.hi1, lm.hi[1:5])
age.hi <- c(tol.pp.hi$age, seq(11,15))
id.hi <- c(tol.pp.hi$id, rep(1, 5))
#plotting the linear fit by id, High Exposure
#id.hi=1 denotes the average for group
interaction.plot(age.hi, id.hi, fit.hi2, ylim=c(0, 4), xlab="AGE", ylab="TOLERANCE", lwd=1)
title(main="High Exposure")
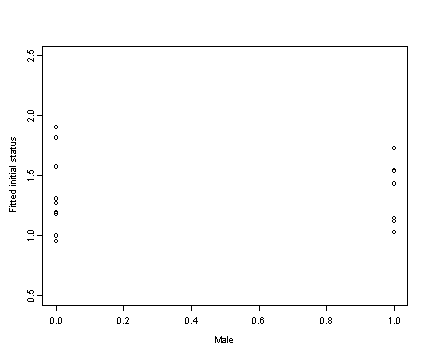
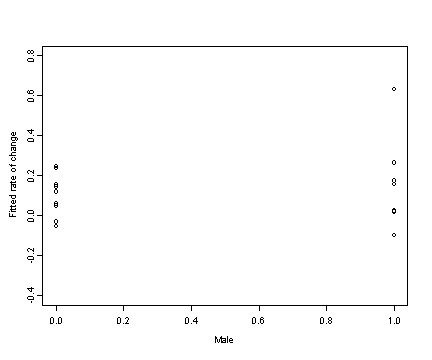
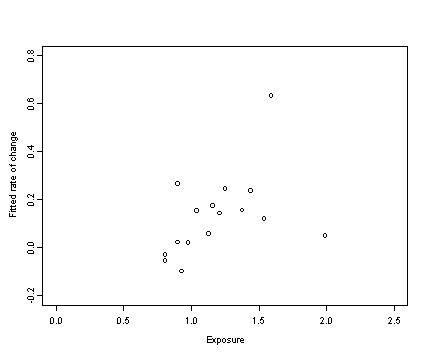
Fig. 2.8, p. 40. OLS estimates plotted against the predictors male and exposure.
#Using the slopes and intercepts from the linear model fitted by id
#generated for use in table 2.3
plot(tolerance$male, ints1, xlab="Male", ylab="Fitted initial status",
xlim=c(0, 1), ylim=c(0.5, 2.5))
cor(tolerance$male, ints1)
[1] 0.008630119
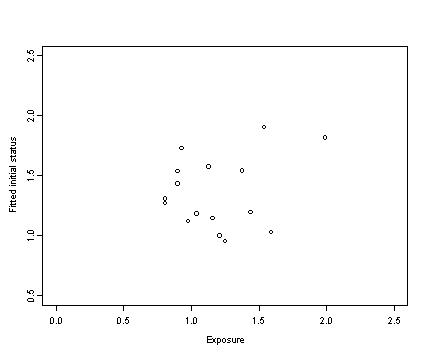
plot(tolerance$exposure, ints1, xlab="Exposure", ylab="Fitted initial status",
xlim=c(0, 2.5), ylim=c(0.5, 2.5))
cor(tolerance$exposure, ints1)
[1] 0.2324426
plot(tolerance$male, slopes1, xlab="Male", ylab="Fitted rate of change",
xlim=c(0, 1), ylim=c(-0.4, .8))
cor(tolerance$male, slopes1) [1] 0.1935703 plot(tolerance$exposure, slopes1, xlab = "Exposure", ylab = "Fitted rate of change", xlim = c(0, 2.5), ylim = c(-0.2, 0.8))
cor(tolerance$exposure, slopes1) [1] 0.4420925