Applied Longitudinal Data Analysis: Modeling Change and Event Occurrence by Judith D. Singer and John B. Willett Chapter 3: Introducing the Multilevel Model for Change
Please note that the “early_int” data file (which is used in Chapter 3) is not included among the data files. This was done at the request of the researchers who contributed this data file to ensure the privacy of the participants in the study. Although the web page shows how to obtain the results with this data file, we regret that visitors do not have access to this file to be able to replicate the results for themselves.
Inputting and printing the early intervention data set, table 3.1, p. 48.
#reading in the early.int data
early.int <- read.table("d:/earlyint_pp.txt", header=T, sep=",")
early.int1 <- early.int[c(1:12, 175:186)
#Table 3.1, p. 48
early.int1
obs id age cog program
1 1 68 1.0 103 1
2 2 68 1.5 119 1
3 3 68 2.0 96 1
4 4 70 1.0 106 1
5 5 70 1.5 107 1
6 6 70 2.0 96 1
7 7 71 1.0 112 1
8 8 71 1.5 86 1
9 9 71 2.0 73 1
10 10 72 1.0 100 1
11 11 72 1.5 93 1
12 12 72 2.0 87 1
13 175 902 1.0 119 0
14 176 902 1.5 93 0
15 177 902 2.0 99 0
16 178 904 1.0 112 0
17 179 904 1.5 98 0
18 180 904 2.0 79 0
19 181 906 1.0 89 0
20 182 906 1.5 66 0
21 183 906 2.0 81 0
22 184 908 1.0 117 0
23 185 908 1.5 90 0
24 186 908 2.0 76 0
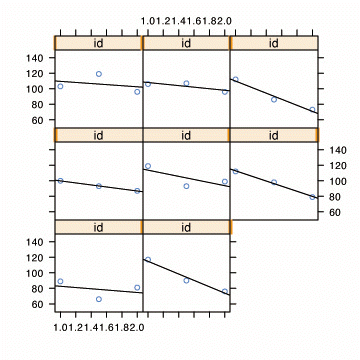
Fig. 3.1, p. 50. OLS trajectories superimposed on the empirical growth plots.
xyplot(cog~age | id, data=early.int1,
panel = function(x, y){
panel.xyplot(x, y)
panel.lmline(x, y)
}, ylim=c(50, 150), as.table=T)
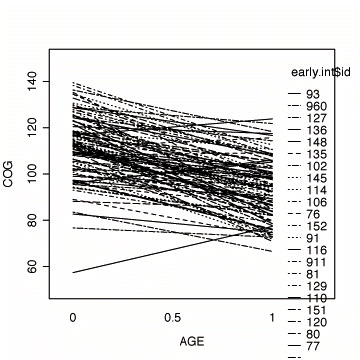
Fig. 3.3, p. 57. Fitted OLS trajectories and stem plots of fitted initial status and fitted rate of change by id.
#fitting the linear model by id fit <- by(early.int, early.int$id, function(data) fitted.values(lm(cog ~ age, data=data))) fit1 <- unlist(fit) names(fit1) <- NULL #plotting the linear fit by id interaction.plot(early.int$age, early.int$id, fit1, xlab="AGE", ylab="COG", ylim=c(50, 150))
#stem plot for fitted initial value
int <- by(early.int, early.int$id,
function(data) coefficients(lm(cog ~ age, data=data))[[1]] )
int <- unlist(int)
names(int) <- NULL
stem(int)
Decimal point is 1 place to the right of the colon
5 | 7
6 |
6 |
7 |
7 | 7
8 | 34
8 | 89
9 | 344
9 | 6666677799
10 | 0012222244
10 | 55666788999
11 | 000111112222333334444
11 | 55677777888999
12 | 12233344
12 | 5556778999
13 | 0013
13 | 55568
14 | 0
#stem plot for fitted rate of change
rate <- by(early.int, early.int$id,
function(data) coefficients(lm(cog ~ age, data=data))[[2]] )
rate <- unlist(rate)
names(rate) <- NULL
stem(rate)
Decimal point is 1 place to the right of the colon
-4 : 443111
-3 : 987
-3 : 443322100000
-2 : 9999877776655
-2 : 44322211110000
-1 : 99888877666655
-1 : 4333322211000
-0 : 99998888777765
-0 : 4444332
0 : 134
0 : 79
1 : 0
1 :
2 : 0
#stem plot for sigma.sq
sig <- by(early.int, early.int$id,
function(data) (summary(lm(cog ~ age, data=data))$sigma)^2 )
sig <- unlist(sig)
names(sig) <- NULL
stem(sig)
Decimal point is 1 place to the right of the colon
0 | 0000111111233334444444466668111113337
2 | 04444888833337778888
4 | 333844
6 | 77734
8 | 1118886666
10 | 44433
12 | 21
14 |
16 | 00011
18 | 3
20 |
22 | 8
24 | 1333
26 | 7
28 | 4
30 |
32 | 3
34 |
36 | 8
38 |
40 | 00
42 |
44 |
46 | 8
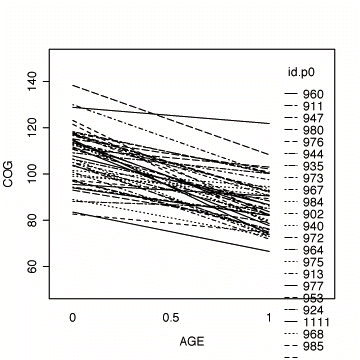
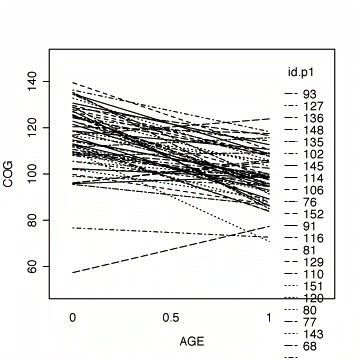
Fig. 3.4, p. 59. The top panel represents fitted OLS trajectories for program=0; the bottom panel represents fitted OLS trajectories for program=1.
#fitting the linear model by id, program=0
early.p0 <- early.int[early.int$program==0, ]
fit.p0 <- by(early.p0, early.p0$id,
function(data) fitted(lm(cog ~ age, data=data)))
fit.p0 <- unlist(fit.p0)
names(fit.p0) <- NULL
#appending the average for the whole group
lm.p0 <- fitted( lm(cog ~ age, data=early.p0) )
names(lm.p0) <- NULL
fit.p0 <- c(fit.p0, lm.p0[1:3])
age.p0 <- c(early.p0$age, c(0, .5, 1))
id.p0 <- c(early.p0$id, rep(1111, 3))
#plotting the linear fit by id
interaction.plot(age.p0, id.p0, fit.p0,
xlab="AGE", ylab="COG", ylim=c(50, 150))
#fitting the linear model by id, program=1
early.p1 <- early.int[early.int$program==1, ]
fit.p1 <- by(early.p1, early.p1$id,
function(data) fitted.values(lm(cog ~ age, data=data)))
fit.p1 <- unlist(fit.p1)
names(fit.p1) <- NULL
#appending the average for the whole group
lm.p1 <- fitted( lm(cog ~ age, data=early.p1) )
names(lm.p1) <- NULL
fit.p1 <- c(fit.p1, lm.p1[1:3])
age.p1 <- c(early.p1$age, c(1, 1.5, 2))
id.p1 <- c(early.p1$id, rep(1111, 3))
#plotting the linear fit by id
interaction.plot(age.p1, id.p1, fit.p1,
xlab="AGE", ylab="COG", ylim=c(50, 150))
Table 3.3, p. 69
library(nlme)
model1<- lme(cog~time*program, data=early.int, random= ~time | id, method="ML")
summary(model1)
AIC BIC logLik
2385.942 2415.809 -1184.971
Random effects:
Formula: ~ time | id
Structure: General positive-definite
StdDev Corr
(Intercept) 11.135975 (Inter
time 3.187612 -0.997
Residual 8.644657
Fixed effects: cog ~ time * program
Value Std.Error DF t-value p-value
(Intercept) 107.8407 2.047915 204 52.65879 <.0001
time -21.1333 1.895694 204 -11.14807 <.0001
program 6.8547 2.729082 101 2.51171 0.0136
time:program 5.2713 2.526229 204 2.08661 0.0382
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-2.347486 -0.5673839 0.02896275 0.5661698 2.330276
Number of Observations: 309
Number of Groups: 103
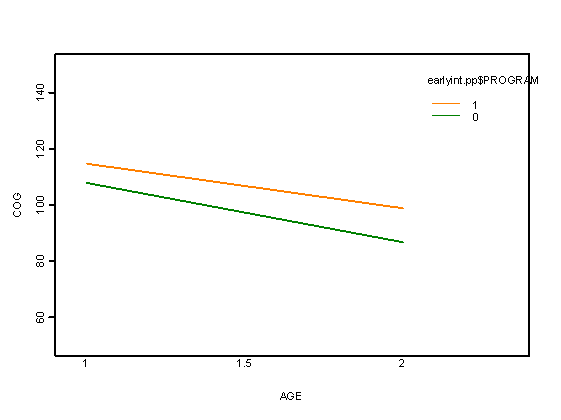
Fig. 3.5 on page 71.
a<-fitted.values(lme(cog~time*program, data=early.int, random= ~time | id, method="REML"))
a<-unlist(a)
interaction.plot(early.int$age, early.int$program, a, xlab="AGE", ylab="COG",
ylim=c(50, 150), lwd=4, lty=1, col=4:5)