Applied Longitudinal Data Analysis: Modeling Change and Event Occurrence by Judith D. Singer and John B. Willett Chapter 6: Modeling Discontinuous and Nonlinear Change
Reading in the wages data set.
wages <- read.table("https://stats.idre.ucla.edu/stat/r/examples/alda/data/wages_pp.txt", header=T, sep=","
Table 6.1, p. 192. Creating the ged*exper variable in the wages data set.
wages$ged.exper <- wages$ged*wages$exper
print(wages[wages$id %in% c(206,2365,4384),c(1:5, 16)])
id lnw exper ged postexp ged.exper
75 206 2.028 1.874 0 0.000 0.000
76 206 2.297 2.814 0 0.000 0.000
77 206 2.482 4.314 0 0.000 0.000
1264 2365 1.782 0.660 0 0.000 0.000
1265 2365 1.763 1.679 0 0.000 0.000
1266 2365 1.710 2.737 0 0.000 0.000
1267 2365 1.736 3.679 0 0.000 0.000
1268 2365 2.192 4.679 1 0.000 4.679
1269 2365 2.042 5.718 1 1.038 5.718
1270 2365 2.320 6.718 1 2.038 6.718
1271 2365 2.665 7.872 1 3.192 7.872
1272 2365 2.418 9.083 1 4.404 9.083
1273 2365 2.389 10.045 1 5.365 10.045
1274 2365 2.485 11.122 1 6.442 11.122
1275 2365 2.445 12.045 1 7.365 12.045
2206 4384 2.859 0.096 0 0.000 0.000
2207 4384 1.532 1.039 0 0.000 0.000
2208 4384 1.590 1.726 1 0.000 1.726
2209 4384 1.969 3.128 1 1.402 3.128
2210 4384 1.684 4.282 1 2.556 4.282
2211 4384 2.625 5.724 1 3.998 5.724
2212 4384 2.583 6.024 1 4.298 6.024
Table 6.2, p. 203.
model.a <- lme(lnw~exper+hgc.9+exper:black+ue.7, wages, random= ~exper | id, method="ML")
2*model.a$logLik
[1] -4830.519
model.b <- lme(lnw~exper+hgc.9+exper:black+ue.7+ged, wages, random= ~ exper+ged | id, method="ML")
2*model.b$logLik
[1] -4805.517
anova(model.a, model.b)
Model df AIC BIC logLik Test L.Ratio p-value
model.a 1 9 4848.519 4909.398 -2415.260
model.b 2 13 4831.517 4919.454 -2402.759 1 vs 2 25.00152 1e-04
model.c <- lme(lnw~exper+hgc.9+exper:black+ue.7+ged, wages, random= ~ exper | id, method="ML")
2*model.c$logLik
[1] -4818.324
anova(model.b, model.c)
Model df AIC BIC logLik Test L.Ratio p-value
model.b 1 13 4831.517 4919.454 -2402.759
model.c 2 10 4838.324 4905.968 -2409.162 1 vs 2 12.80671 0.0051
model.d <- lme(lnw~exper+hgc.9+exper:black+ue.7+postexp, wages, random= ~exper+postexp | id, method="ML")
2*model.d$logLik
[1] -4817.377
anova(model.a, model.d)
Model df AIC BIC logLik Test L.Ratio p-value
model.a 1 9 4848.519 4909.398 -2415.260
model.d 2 13 4843.377 4931.314 -2408.689 1 vs 2 13.1417 0.0106
model.e <- lme(lnw~exper+hgc.9+exper:black+ue.7+postexp, wages, random= ~exper | id, method="ML")
2*model.e$logLik
[1] -4820.706
anova(model.d, model.e)
Model df AIC BIC logLik Test L.Ratio p-value
model.d 1 13 4843.377 4931.314 -2408.689
model.e 2 10 4840.706 4908.350 -2410.353 1 vs 2 3.329158 0.3436
model.f <- lme(lnw~exper+hgc.9+exper:black+ue.7+postexp+ged, wages, random= ~exper+postexp+ged | id, method="ML")
2*model.f$logLik
[1] -4789.354
anova(model.b, model.f)
Model df AIC BIC logLik Test L.Ratio p-value
model.b 1 13 4831.517 4919.454 -2402.759
model.f 2 18 4825.354 4947.113 -2394.677 1 vs 2 16.16339 0.0064
anova(model.d, model.f)
Model df AIC BIC logLik Test L.Ratio p-value
model.d 1 13 4843.377 4931.314 -2408.689
model.f 2 18 4825.354 4947.113 -2394.677 1 vs 2 28.02321 <.0001
model.g <- lme(lnw~exper+hgc.9+exper:black+ue.7+postexp+ged, wages, random= ~exper+ged | id, method="ML")
2*model.g$logLik
[1] -4802.688
anova(model.f, model.g)
Model df AIC BIC logLik Test L.Ratio p-value
model.f 1 18 4825.354 4947.113 -2394.677
model.g 2 14 4830.688 4925.390 -2401.344 1 vs 2 13.33432 0.0098
model.h <- lme(lnw~exper+hgc.9+exper:black+ue.7+postexp+ged, wages, random= ~exper+postexp | id, method="ML")
2*model.h$logLik
[1] -4812.639
anova(model.f, model.h)
Model df AIC BIC logLik Test L.Ratio p-value
model.f 1 18 4825.354 4947.113 -2394.677
model.h 2 14 4840.639 4935.340 -2406.320 1 vs 2 23.28511 1e-04
***model.i <- lme(lnw~exper+hgc.9+exper:black+ue.7+ged+exper:ged, wages, random= ~exper+ged+exper:ged | id, method="ML")
2*model.i$logLik
[1] -4798.705
***anova(model.b, model.i)
Model df AIC BIC logLik Test L.Ratio p-value
model.b 1 13 4831.519 4919.455 -2402.759
model.i 2 18 4834.705 4956.464 -2399.353 1 vs 2 6.813514 0.2349
model.j <- lme(lnw~exper+hgc.9+exper:black+ue.7+ged+exper:ged, wages, random= ~exper+ged | id, method="ML")
2*model.j$logLik
[1] -4804.601
***anova(model.i, model.j)
Model df AIC BIC logLik Test L.Ratio p-value
model.i 1 18 4834.705 4956.464 -2399.353
model.j 2 14 4832.628 4927.329 -2402.314 1 vs 2 5.92252 0.205
Table 6.3, p. 205. Summary of model F.
summary(model.f)
Linear mixed-effects model fit by maximum likelihood
Data: wages
AIC BIC logLik
4825.354 4947.113 -2394.677
Random effects:
Formula: ~exper + postexp + ged | id
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
(Intercept) 0.20327713 (Intr) exper postxp
exper 0.03688142 -0.227
postexp 0.05785090 -0.513 -0.425
ged 0.12828189 0.457 0.616 -0.528
Residual 0.30638530
Fixed effects: lnw ~ exper + hgc.9 + exper:black + ue.7 + postexp + ged
Value Std.Error DF t-value p-value
(Intercept) 1.7385724 0.011948806 5509 145.50177 0.0000
exper 0.0414714 0.002798481 5509 14.81925 0.0000
hgc.9 0.0390263 0.006246189 886 6.24801 0.0000
ue.7 -0.0117239 0.001783798 5509 -6.57244 0.0000
postexp 0.0094225 0.005548605 5509 1.69818 0.0895
ged 0.0408782 0.022006748 5509 1.85753 0.0633
exper:black -0.0196196 0.004472637 5509 -4.38657 0.0000
Correlation:
(Intr) exper hgc.9 ue.7 postxp ged
exper -0.531
hgc.9 0.093 -0.023
ue.7 -0.368 0.255 -0.045
postexp 0.159 -0.368 -0.021 -0.012
ged -0.323 0.122 -0.020 0.055 -0.558
exper:black -0.059 -0.297 -0.018 0.067 -0.056 0.007
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-4.34624959 -0.51331005 -0.03870199 0.44566634 6.97197858
Number of Observations: 6402
Number of Groups: 888
Fig. 6.4, p. 209. We must first read in the alcohol data set and then run model e from table 4.1, p. 94.
#reading in the alcohol data
alcohol <- read.table("https://stats.idre.ucla.edu/stat/r/examples/alda/data/alcohol1_pp.txt", header=T, sep=",")
#table 4.1, model e
model.e <- lme(alcuse~coa+peer*age_14 , data=alcohol, random= ~ age_14 | id, method="ML")
#obtaining the fixed effects parameters
fixef.e <- fixef(model.e)
#obtaining the predicted values and squaring them
fit2.ec0p0 <- (fixef.e[[1]] + .655*fixef.e[[3]] +
alcohol$age_14[1:3]*fixef.e[[4]] +
.655*alcohol$age_14[1:3]*fixef.e[[5]])^2
fit2.ec0p1 <- (fixef.e[[1]] + 1.381*fixef.e[[3]] +
alcohol$age_14[1:3]*fixef.e[[4]] +
1.381*alcohol$age_14[1:3]*fixef.e[[5]] )^2
fit2.ec1p0 <- (fixef.e[[1]] + fixef.e[[2]] + .655*fixef.e[[3]] +
alcohol$age_14[1:3]*fixef.e[[4]] +
.655*alcohol$age_14[1:3]*fixef.e[[5]] )^2
fit2.ec1p1 <- (fixef.e[[1]] + fixef.e[[2]] + 1.381*fixef.e[[3]] +
alcohol$age_14[1:3]*fixef.e[[4]] +
1.381*alcohol$age_14[1:3]*fixef.e[[5]])^2
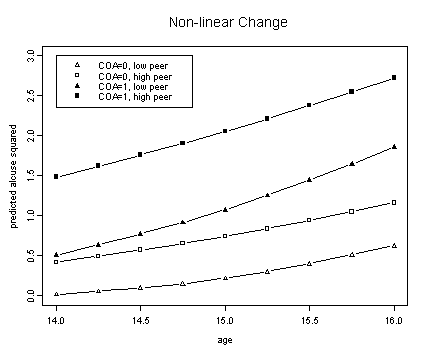
plot(alcohol$age[1:3], fit2.ec0p0, ylim=c(0, 3), type="n",
ylab="predicted alcuse squared", xlab="age")
lines(spline(alcohol$age[1:3], fit2.ec0p0), pch=2, type="b")
lines(spline(alcohol$age[1:3], fit2.ec0p1), type="b", pch=0)
lines(spline(alcohol$age[1:3], fit2.ec1p0), type="b", pch=17)
lines(spline(alcohol$age[1:3], fit2.ec1p1), type="b", pch=15)
title("Non-linear Change")
legend(14, 3, c("COA=0, low peer", "COA=0, high peer",
"COA=1, low peer", "COA=1, high peer"))
Reading in the berkeley data set and then creating the transformed variables for iq and age.
berkeley <- read.table("https://stats.idre.ucla.edu/stat/r/examples/alda/data/berkeley_pp.txt", header=T, sep=",")
berkeley$age2.3 <- berkeley$age^(1/2.3)
berkeley$iq2.3 <- berkeley$iq^2.3
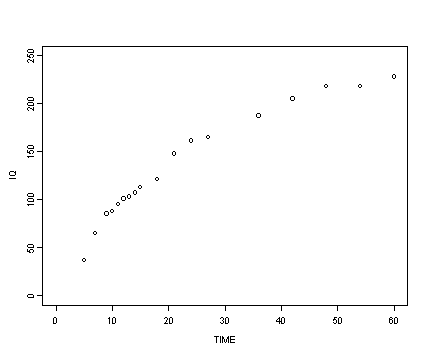
Fig. 6.6, p. 212.
plot(berkeley$age, berkeley$iq, type="p", ylim=c(0, 250), xlim=c(0, 60), ylab="IQ", xlab="TIME")
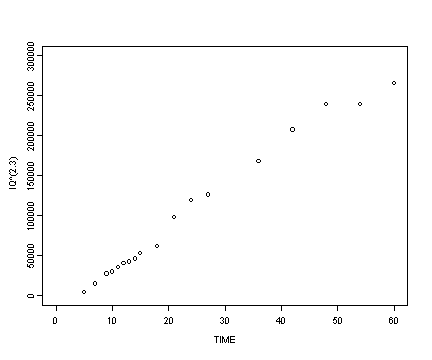
plot(berkeley$age, berkeley$iq2.3, type="p", ylim=c(0, 300000), xlim=c(0, 60), ylab="IQ^(2.3)", xlab="TIME")
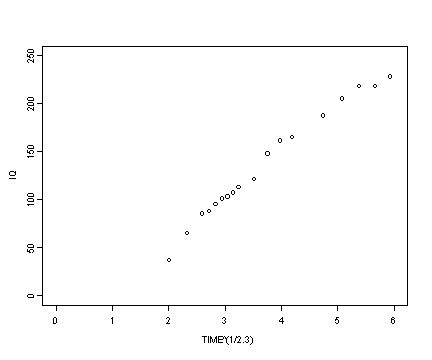
plot(berkeley$age2.3, berkeley$iq, type="p", ylim=c(0, 250), xlim=c(0, 6), ylab="IQ", xlab="TIME^(1/2.3)")
Reading in the external data set.
external <- read.table("https://stats.idre.ucla.edu/wp-content/uploads/2020/01/external_pp.txt", header=T, sep=",")
Creating the higher order variables for grade.
external$grade2 <- external$grade^2 external$grade3 <- external$grade^3 external$grade4 <- external$grade^4
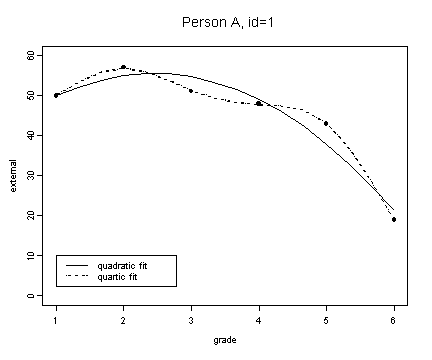
Fig. 6.7, p. 218.
fit1 <- fitted.values(lm(external~grade+grade2, external[external$id==1,]))
fit1.4 <- fitted.values(lm(external~grade+grade2+grade3+grade4, external[external$id==1,]))
plot(spline(external[external$id==1,]$grade, fit1), type="l", ylim=c(0, 60), ylab="external", xlab="grade")
lines(spline(external[external$id==1,]$grade, fit1.4), type="l", lty=3)
points(external[external$id==1,]$grade, external[external$id==1,]$external, pch=16)
title("Person A, id=1")
legend(1, 10, c("quadratic fit", "quartic fit"), lty=c(1, 3))
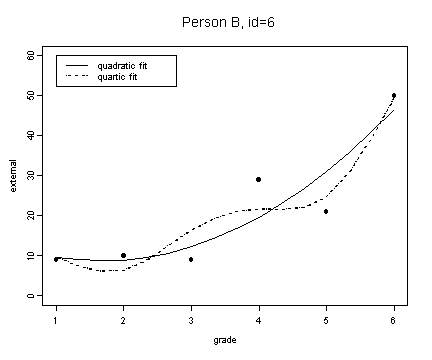
fit2 <- fitted.values(lm(external~grade+grade2, external[external$id==6,]))
fit2.4 <- fitted.values(lm(external~grade+grade2+grade3+grade4, external[external$id==6,]))
plot(spline(external[external$id==6,]$grade, fit2), type="l", ylim=c(0, 60), ylab="external", xlab="grade")
lines(spline(external[external$id==6,]$grade, fit2.4), type="l", lty=3)
points(external[external$id==6,]$grade, external[external$id==6,]$external, pch=16)
title("Person B, id=6")
legend(1, 60, c("quadratic fit", "quartic fit"), lty=c(1, 3))
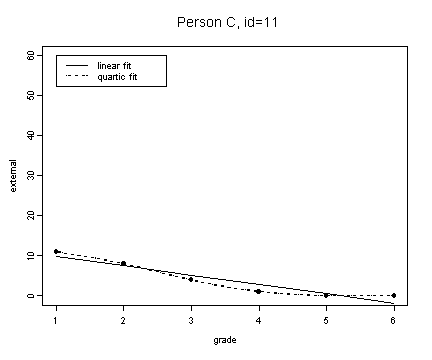
fit3 <- fitted.values(lm(external~grade, external[external$id==11,]))
fit3.4 <- fitted.values(lm(external~grade+grade2+grade3+grade4, external[external$id==11,]))
plot(external[external$id==11,]$grade, fit3, type="l", ylim=c(0, 60), ylab="external", xlab="grade")
lines(spline(external[external$id==11,]$grade, fit3.4), type="l", lty=3)
points(external[external$id==11,]$grade, external[external$id==11,]$external, pch=16)
title("Person C, id=11")
legend(1, 60, c("linear fit", "quartic fit"), lty=c(1, 3))
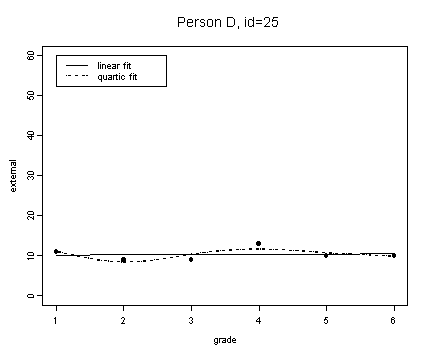
fit4 <- fitted.values(lm(external~grade, external[external$id==25,]))
fit4.4 <- fitted.values(lm(external~grade+grade2+grade3+grade4, external[external$id==25,]))
plot(external[external$id==25,]$grade, fit4, type="l", ylim=c(0, 60), ylab="external", xlab="grade")
lines(spline(external[external$id==25,]$grade, fit4.4), type="l", lty=3)
points(external[external$id==25,]$grade, external[external$id==25,]$external, pch=16)
title("Person D, id=25")
legend(1, 60, c("linear fit", "quartic fit"), lty=c(1, 3))
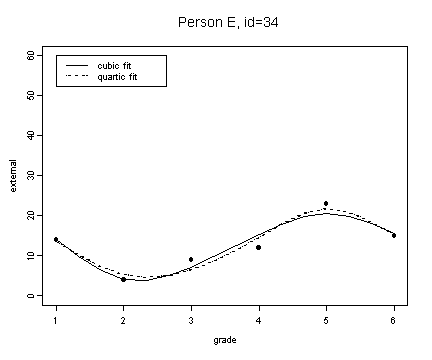
fit5 <- fitted.values(lm(external~grade+grade2+grade3, external[external$id==34,]))
fit5.4 <- fitted.values(lm(external~grade+grade2+grade3+grade4, external[external$id==34,]))
plot(spline(external[external$id==34,]$grade, fit5), type="l", ylim=c(0, 60), ylab="external", xlab="grade")
lines(spline(external[external$id==34,]$grade, fit5.4), type="l", lty=3)
points(external[external$id==34,]$grade, external[external$id==34,]$external, pch=16)
title("Person E, id=34")
legend(1, 60, c("cubic fit", "quartic fit"), lty=c(1, 3))
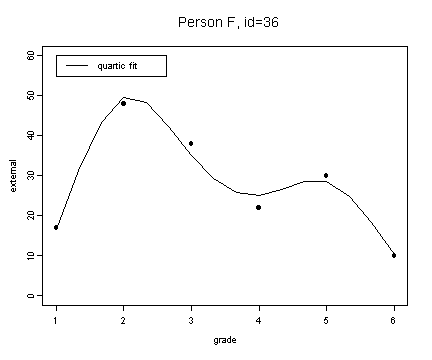
fit6.4 <- fitted.values(lm(external~grade+grade2+grade3+grade4, external[external$id==36,]))
plot(spline(external[external$id==36,]$grade, fit6.4), type="l", ylim=c(0, 60), ylab="external", xlab="grade")
points(external[external$id==36,]$grade, external[external$id==36,]$external, pch=16)
title("Person F, id=36")
legend(1, 60, c("quartic fit"), lty=1)
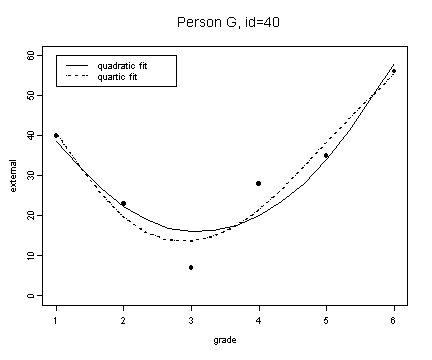
fit7 <- fitted.values(lm(external~grade+grade2, external[external$id==40,]))
fit7.4 <- fitted.values(lm(external~grade+grade2+grade3+grade4, external[external$id==40,]))
plot(spline(external[external$id==40,]$grade, fit7), type="l", ylim=c(0, 60), ylab="external", xlab="grade")
lines(spline(external[external$id==40,]$grade, fit7.4), type="l", lty=3)
points(external[external$id==40,]$grade, external[external$id==40,]$external, pch=16)
title("Person G, id=40")
legend(1, 60, c("quadratic fit", "quartic fit"), lty=c(1, 3))
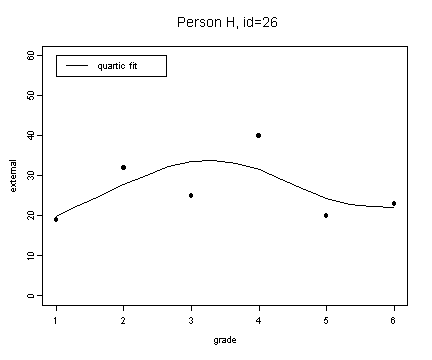
fit8.4 <- fitted.values(lm(external~grade+grade2+grade3+grade4, external[external$id==26,]))
plot(spline(external[external$id==26,]$grade, fit8.4), type="l", ylim=c(0, 60), ylab="external", xlab="grade")
points(external[external$id==26,]$grade, external[external$id==26,]$external, pch=16)
title("Person H, id=26")
legend(1, 60, c("quartic fit"), lty=1
Creating the higher order terms for time in the external data set.
external$time2 <- external$time^2 external$time3 <- external$time^3
Table 6.5, p. 221. Comparison of fitting alternative polynomial change trajectories to the external data set.
model.a <- lme(external ~ 1, random = ~ 1 | id, method = "ML", external)
summary(model.a)
Linear mixed-effects model fit by maximum likelihood
Data: external
AIC BIC logLik
2016.253 2027.048 -1005.127
Random effects:
Formula: ~1 | id
(Intercept) Residual
StdDev: 9.349753 8.378721
Fixed effects: external ~ 1
Value Std.Error DF t-value p-value
(Intercept) 12.96296 1.486882 225 8.718217 0
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-2.6629105 -0.5254597 -0.1648188 0.4803230 3.5392935
Number of Observations: 270
Number of Groups: 45
model.b <- lme(external ~ time, random = ~ time | id, method = "ML", external)
summary(model.b)
Linear mixed-effects model fit by maximum likelihood
Data: external
AIC BIC logLik
2003.744 2025.335 -995.8722
Random effects:
Formula: ~time | id
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
(Intercept) 11.114141 (Intr)
time 2.166306 -0.521
Residual 7.329261
Fixed effects: external ~ time
Value Std.Error DF t-value p-value
(Intercept) 13.289947 1.8426669 224 7.212344 0.000
time -0.130794 0.4168777 224 -0.313746 0.754
Correlation:
(Intr)
time -0.589
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-2.9551932 -0.4927453 -0.1353043 0.4206586 2.8078552
Number of Observations: 270
Number of Groups: 45
model.c <- lme(external ~ time+time2, random = ~ time+time2 | id, method = "ML", external)
summary(model.c)
Linear mixed-effects model fit by maximum likelihood
Data: external
AIC BIC logLik
1995.836 2031.821 -987.9182
Random effects:
Formula: ~time + time2 | id
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
(Intercept) 10.348277 (Intr) time
time 4.960841 -0.072
time2 1.102567 -0.119 -0.908
Residual 6.479472
Fixed effects: external ~ time + time2
Value Std.Error DF t-value p-value
(Intercept) 13.969841 1.783654 223 7.832146 0.0000
time -1.150635 1.112977 223 -1.033835 0.3023
time2 0.203968 0.229323 223 0.889436 0.3747
Correlation:
(Intr) time
time -0.322
time2 0.131 -0.932
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-2.2152282 -0.4833639 -0.1148441 0.3780750 2.6531221
Number of Observations: 270
Number of Groups: 45
***model.d <- lme(external ~ time+time2+time3, random = ~ time+time2+time3 | id, method = "ML", external)
update(model.a, formula = external ~ time + time2 + time3, random
= ~ time + time2 + time3 | id)
summary(model.d)
Linear mixed-effects model fit by maximum likelihood
Data: external
AIC BIC logLik
1997.36 2051.336 -983.6798
Random effects:
Formula: ~ time + time2 + time3 | id
Structure: General positive-definite
StdDev Corr
(Intercept) 11.3456161 (Intr) time time2
time 10.3276727 -0.472
time2 4.0747529 0.521 -0.975
time3 0.4190613 -0.672 0.940 -0.981
Residual 6.1485004
Fixed effects: external ~ time + time2 + time3
Value Std.Error DF t-value p-value
(Intercept) 13.79453 1.929355 222 7.149815 <.0001
time -0.35006 2.344248 222 -0.149327 0.8814
time2 -0.23430 1.066569 222 -0.219680 0.8263
time3 0.05844 0.130845 222 0.446605 0.6556
Reading in the fox and geese data.
fg <- read.table("https://stats.idre.ucla.edu/stat/r/examples/alda/data/foxngeese_pp.txt", header=T, sep=",")
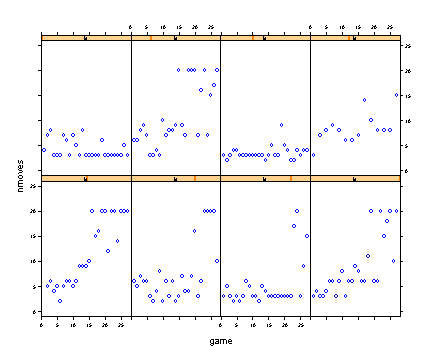
Fig. 6.8, p. 227. Empirical growth plots for 8 children in the fox and geese data.
xyplot(nmoves~game | id, data=fg[fg$id %in% c(1, 4, 6, 7, 8, 11, 12, 15), ], ylim=c(0, 25), as.table=T)
Table 6.6, p. 231. Fitting a logistic model to the fox and geese data.
Notice, this model does not correspond to equation (6.8) in the book. Instead, it corresponds to the following equation:
Yij = 1 + 19/(1 + π0*exp(- (π1+u1)*Time – u0)) + εij
model.a <- nlme(nmoves~ 1 + 19/ (1 + xmid*exp( -scal*game + u)),
fixed=scal+xmid~1, random= scal+u~1 |id,
start=c(scal=.2, xmid=12), data=fg)
summary(model.a)
Nonlinear mixed-effects model fit by maximum likelihood
Model: nmoves ~ 1 + 19/(1 + xmid * exp(-scal * game + u))
Data: fg
AIC BIC logLik
2493.691 2518.28 -1240.846
Random effects:
Formula: list(scal ~ 1, u ~ 1)
Level: id
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
scal 0.07502426 scal
u 0.67804085 0.821
Residual 3.67947375
Fixed effects: scal + xmid ~ 1
Value Std.Error DF t-value p-value
scal 0.113036 0.0201006 427 5.623499 0
xmid 10.741633 2.3508149 427 4.569323 0
Correlation:
scal
xmid 0.817
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-2.6168059 -0.5637294 -0.1259907 0.5704615 3.5385187
Number of Observations: 445
Number of Groups: 17
model.b <- nlme(nmoves~ 1 + 19/(1+xmid*exp(-scal10*game -scal01*read -scal11*read*game + u)),
fixed=scal10+scal01+scal11+xmid~1, random= scal10+u~1 |id,
start=c(scal10=.12, scal01= -.4, scal11= .04, xmid=12), data=fg)
summary(model.b)
Nonlinear mixed-effects model fit by maximum likelihood
Model: nmoves ~ 1 + 19/(1 + xmid * exp(-scal10 * game - scal01 * read - scal11 * read * game + u))
Data: fg
AIC BIC logLik
2495.652 2528.436 -1239.826
Random effects:
Formula: list(scal10 ~ 1, u ~ 1)
Level: id
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
scal10 0.06864467 scal10
u 0.61433603 0.783
Residual 3.68126652
Fixed effects: scal10 + scal01 + scal11 + xmid ~ 1
Value Std.Error DF t-value p-value
scal10 0.041173 0.051314 425 0.8023701 0.4228
scal01 -0.331583 0.272499 425 -1.2168222 0.2243
scal11 0.036792 0.024578 425 1.4969888 0.1351
xmid 5.636007 3.175306 425 1.7749494 0.0766
Correlation:
scal10 scal01 scal11
scal01 0.736
scal11 -0.931 -0.796
xmid 0.793 0.929 -0.743
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-2.5945179 -0.5869666 -0.1254558 0.5679836 3.5759761
Number of Observations: 445
Number of Groups: 17
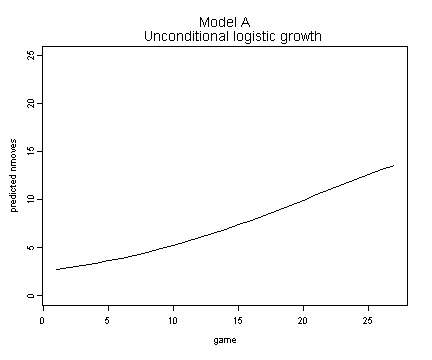
Fig. 6.10, p. 232.
fixef.a <- fixef(model.a)
fit.a <- 1 + 19/(1 + fixef.a[[2]]*exp(-fixef.a[[1]]*fg$game[1:27]))
plot(fg$game[1:27], fit.a, ylim=c(0, 25), type="l", ylab="predicted nmoves", xlab="game")
title("Model A \n Unconditional logistic growth")
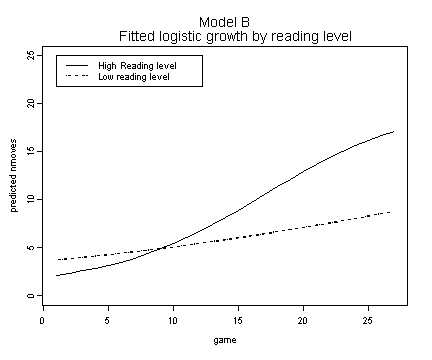
fixef.b <- fixef(model.b)
fit.b.high <- 1 + 19/(1+fixef.b[[4]]*exp(-fixef.b[[1]]*fg$game[1:27] - fixef.b[[2]]*1.58 - fixef.b[[3]]*1.58*fg$game[1:27]))
fit.b.low <- 1 + 19/(1+fixef.b[[4]]*exp(-fixef.b[[1]]*fg$game[1:27] - fixef.b[[2]]*(-1.58) - fixef.b[[3]]*(-1.58)*fg$game[1:27]))
plot(fg$game[1:27], fit.b.high, ylim=c(0, 25), type="l",
ylab="predicted nmoves", xlab="game")
lines(fg$game[1:27], fit.b.low, lty=3)
title("Model B \n Fitted logistic growth by reading level")
legend(1, 25, c("High Reading level","Low reading level"), lty=c(1, 3)