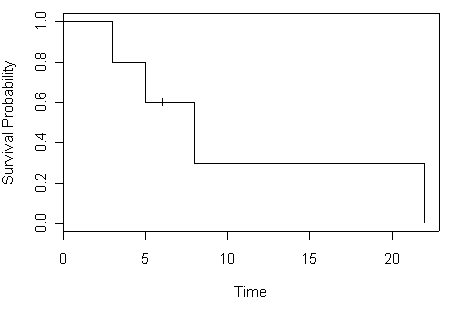The R packages needed for this chapter are the survival package and the KMsurv package. We currently use R 2.0.1 patched version. You may want to make sure that packages on your local machine are up to date. You can perform update in R using update.packages() function.
Table 2.1 using a subset of data set hmohiv.
hmohiv<-read.table("https://stats.idre.ucla.edu/stat/r/examples/asa/hmohiv.csv", sep=",", header = TRUE)
library(survival)
attach(hmohiv)
mini<-hmohiv[ID<=5,]
mini
ID time age drug censor entdate enddate
1 1 5 46 0 1 5/15/1990 10/14/1990
2 2 6 35 1 0 9/19/1989 3/20/1990
3 3 8 30 1 1 4/21/1991 12/20/1991
4 4 3 30 1 1 1/3/1991 4/4/1991
5 5 22 36 0 1 9/18/1989 7/19/1991
Table 2.2 on page 32 using data set created for Table 2.1 previously. We use the conf.type=”none” argument to specify that we do not want to include any confidence intervals for the survival function.
attach(mini) mini.surv time n.risk n.event survival std.err 3 5 1 0.8 0.179 5 4 1 0.6 0.219 8 2 1 0.3 0.239 22 1 1 0.0 NA
Figure 2.1 on page 32 based on Table 2.2.
plot(mini.surv, xlab="Time", ylab="Survival Probability")
Figure 2.2 and Table 2.3 on page 34 and 35 using the entire data set hmohiv.
detach(mini)
attach(hmohiv)
hmohiv.surv
time n.risk n.event survival std.err
1 100 15 0.8500 0.0357
2 83 5 0.7988 0.0402
3 73 10 0.6894 0.0473
...................................
53 7 1 0.0934 0.0349
54 6 1 0.0778 0.0324
57 4 1 0.0584 0.0296
58 3 1 0.0389 0.0253
plot (hmohiv.surv, xlab="Time", ylab="Survival Probability" )
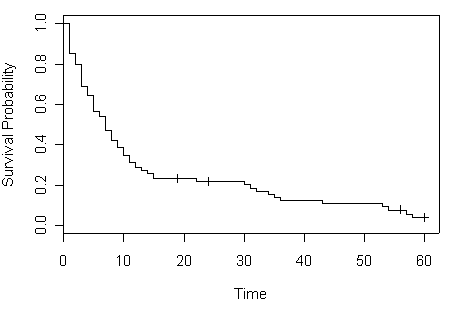
Table 2.4 on page 38 using data set hmohiv with life-table estimator. We will use lifetab function presented in package KMsurv. You can download the package from CRAN by typing from the R prompt install.packages(“KMsurv”). In order to be able to use function lifetab, we need to create a couple of variables, mainly the number of censored at each time point and the number of events at each time point. Also notice that the time intervals have been grouped. The first step is to create grouped data. We use function gsummary from package nlme here to create grouped data. Based on the grouped data, we will create a couple of new variables for lifetab. Function lifetab requires that the length of the time variable is 1 greater than other variables, such as the variable of number of events, or the variable of number of censored.
library(KMsurv) library(nlme) t6m<-floor(time/6) tall<-data.frame(t6m, censor) die<-gsummary(tall, sum, groups=t6m) total<-gsummary(tall, length, groups=t6m) rm(t6m) ltab.data<-cbind(die[,1:2], total[,2]) detach(hmohiv) attach(ltab.data) lt=length(t6m) t6m[lt+1]=NA nevent=censor nlost=total[,2] - censor mytable<-lifetab(t6m, 100, nlost, nevent) mytable[,1:5]
nsubs nlost nrisk nevent surv 0-1 100 10 95.0 41 1.00000000 1-2 49 3 47.5 21 0.56842105 2-3 25 2 24.0 6 0.31711911 3-4 17 1 16.5 1 0.23783934 4-5 15 1 14.5 0 0.22342483 5-6 14 0 14.0 5 0.22342483 6-7 9 0 9.0 1 0.14363025 7-8 8 0 8.0 1 0.12767133 8-9 7 0 7.0 1 0.11171242 9-10 6 1 5.5 3 0.09575350 10-NA 2 2 1.0 0 0.04352432
Figure 2.3 and Figure 2.4 on page 38-39 based on Table 2.4 from previous example.
plot(t6m[1:11], mytable[,5], type="s", xlab="Survival time in every 6 month",
ylab="Proportion Surviving")
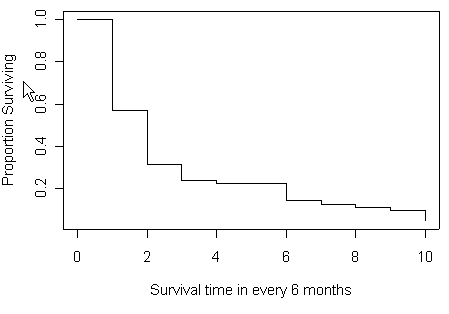
plot(t6m[1:11], mytable[,5], type="b", xlab="Survival time in every 6 month",
ylab="Proportion Surviving")
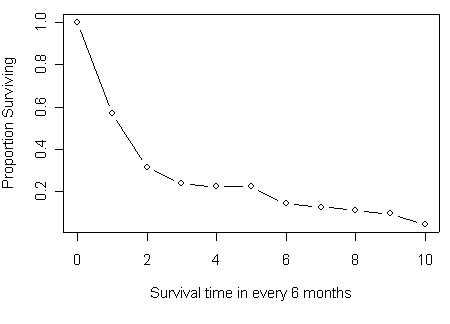
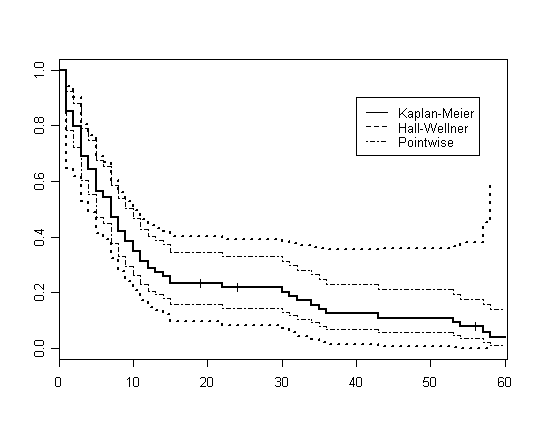
Figure 2.5 on page 46.
library(survival)
library(km.ci)
hmohiv.surv <- survfit( Surv(time, censor) ~ 1)
a<-km.ci(hmohiv.surv, conf.level=0.95, tl=NA, tu=NA, method="loghall")
par(cex=.8)
plot(a, lty=2, lwd=2)
time.conf <- survfit( Surv(time, censor)~ 1)
lines(time.conf, lwd=2, lty=1)
lines(time.conf, lwd=1, lty=4, conf.int=T)
linetype<-c(1, 2, 4)
legend(40, .9, c("Kaplan-Meier", "Hall-Wellner", "Pointwise"), lty=(linetype))
Figure 2.6 on page 48 using the mini data.
detach() attach(mini) mini.surv <- survfit(Surv(time, censor)~ 1, conf.type="none") summary(mini.surv)
time n.risk n.event survival std.err
3 5 1 0.8 0.179
5 4 1 0.6 0.219
8 2 1 0.3 0.239
22 1 1 0.0 NA
par(cex=.8) plot(mini.surv, xlab="Time", ylab="Survival Probability") lines(x=c(5,5),y=c(0,.6), lty=2) lines(x=c(8,8),y=c(0,.3), lty=2) lines(x=c(0,22),y=c(.25,.25), lty=2) lines(x=c(0,8),y=c(.5,.5), lty=2) lines(x=c(0,5),y=c(.75,.75), lty=2)
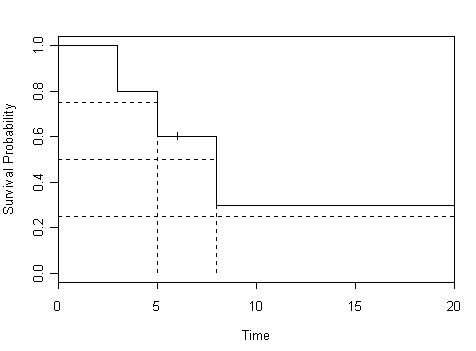
Table 2.5 on page 50, estimating quartiles using the full hmohiv data set. The confidence intervals in the book are calculated based on the standard errors. We write a function called stci for this calculation. Here is the definition of stci:
stci = function(qn, y)
{
temp<-data.frame(time=y$time, surv=y$surv, std.err=y$std.err)
temp$std.err<-temp$std.err*temp$surv
attach(temp)
q.lp<-temp[surv<= qn/100 -.05,][1,]
q<-temp[surv<=qn/100,][1,]
q.u<-temp[surv>=qn/100+.05,]
rnm<-nrow(q.u)
q.up<-q.u[rnm, ]
fp = (q.up$surv - q.lp$surv)/( q.lp$time - q.up$time)
std = (q$std.err)/fp
lower = q$time - 1.96*std
upper = q$time + 1.96*std
print(rbind(c(quantile=qn, time=q$time, std.err=std, cie.lower=lower, cie.upper=upper)))
}
Now we can create the table using this function.
rm(list=ls()) #cleaning up
hmohiv<-read.table("https://stats.idre.ucla.edu/stat/r/examples/asa/hmohiv.csv", sep=",", header = TRUE)
library(survival)
attach(hmohiv)
h.surv <- survfit(Surv(time, censor)~ 1, conf.type="log-log")
stci(75, h.surv)
quantile time std.err cie.lower cie.upper [1,] 75 3 0.5891626 1.845241 4.154759 stci(50, h.surv)
quantile time std.err cie.lower cie.upper [1,] 50 7 1.114345 4.815884 9.184116 /* Note: there is a typo error in the book for the lower value of the confidence interval */ stci(25, h.surv) quantile time std.err cie.lower cie.upper [1,] 25 15 7.451834 0.3944059 29.60559
Table 2.6 on page 52 based on the object h.surv created in previous example.
/* Note: there is a typo error for the upper confidence interval for time 4 */
summary(h.surv)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
1 100 15 0.8500 0.0357 0.76359 0.907
2 83 5 0.7988 0.0402 0.70566 0.865
3 73 10 0.6894 0.0473 0.58622 0.772
4 61 4 0.6442 0.0493 0.53868 0.731
5 56 7 0.5636 0.0517 0.45636 0.658
6 49 2 0.5406 0.0521 0.43343 0.636
7 46 6 0.4701 0.0526 0.36440 0.569
8 39 4 0.4219 0.0525 0.31832 0.522
9 35 3 0.3857 0.0520 0.28454 0.486
..................more output omitted .........................
The mean of the survivorship function, p. 57 based on h.surv created previously.
print(h.surv, show.rmean=T)
n events rmean se(rmean) median 0.95LCL 0.95UCL
100.00 80.00 14.67 1.97 7.00 5.00 9.00
Figure 2.7 on page 58 using hmohiv data set.
timestrata.surv <- survfit( Surv(time, censor)~ strata(drug), hmohiv, conf.type=”log-log”) plot(timestrata.surv, lty=c(1,3), xlab=”Time”, ylab=”Survival Probability”) legend(40, 1.0, c(“Drug – No”, “Drug – Yes”) , lty=c(1,3) )
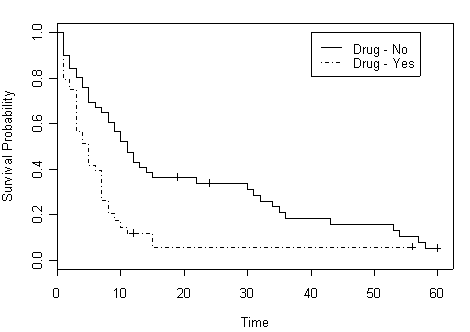
Table 2.8 on page 63, a smaller version of data set hmohiv.
rm(list=ls()) #cleaning up
minitest<-read.table("https://stats.idre.ucla.edu/stat/r/examples/asa/minitest.txt", header = TRUE)
attach(minitest)
minitest
time censor drug
1 3 1 0
2 4 0 0
3 5 1 0
4 22 1 0
5 34 1 0
6 2 1 1
7 3 1 1
8 4 0 1
9 7 1 1
10 11 1 1
Table 2.9 on page 64 using the data set created in previous example.
Table 2.10 on page 64 testing survivor curves using the minitest data set.
We will use survdiff for tests. Function survdiff is a family of tests parameterized by parameter rho. The following description is from R Documentation on survdiff: “This function implements the G-rho family of Harrington and Fleming (1982, A class of rank test procedures for censored survival data. _Biometrika_ *69*, 553-566.), with weights on each death of S(t)^rho, where S is the Kaplan-Meier estimate of survival. With ‘rho = 0’ this is the log-rank or Mantel-Haenszel test, and with ‘rho = 1’ it is equivalent to the Peto & Peto modification of the Gehan-Wilcoxon test.”
survdiff(Surv(time, censor) ~ drug, data=minitest, rho=0)
N Observed Expected (O-E)^2/E (O-E)^2/V
drug=0 5 4 5.38 0.353 1.36
drug=1 5 4 2.62 0.724 1.36
Chisq= 1.4 on 1 degrees of freedom, p= 0.243
survdiff(Surv(time, censor) ~ drug, data=minitest, rho=1)
N Observed Expected (O-E)^2/E (O-E)^2/V
drug=0 5 2.02 2.9 0.267 0.927
drug=1 5 2.88 2.0 0.387 0.927
Chisq= 0.9 on 1 degrees of freedom, p= 0.336
Table 2.11 on page 65 testing for differences between drug group.
rm(list=ls()) #cleaning up
hmohiv<-read.table("https://stats.idre.ucla.edu/stat/r/examples/asa/hmohiv.csv", sep=",", header = TRUE)
attach(hmohiv)
survdiff(Surv(time, censor) ~ drug, rho=0)
N Observed Expected (O-E)^2/E (O-E)^2/V
drug=0 51 42 54.9 3.02 11.9
drug=1 49 38 25.1 6.60 11.9
Chisq= 11.9 on 1 degrees of freedom, p= 0.000575
survdiff(Surv(time, censor) ~ drug, data=hmohiv, rho=1)
N Observed Expected (O-E)^2/E (O-E)^2/V
drug=0 51 20.0 29.3 2.94 11.7
drug=1 49 27.7 18.4 4.69 11.7
Chisq= 11.7 on 1 degrees of freedom, p= 0.000622
Table 2.12 on page 65. We will create a categorical age variable, agecat first.
agecat
n events median 0.95LCL 0.95UCL
strata(agecat)=agecat=(19.9,29] 12 8 43 5 Inf
strata(agecat)=agecat=(29,34] 34 29 9 6 12
strata(agecat)=agecat=(34,39] 25 20 7 3 9
strata(agecat)=agecat=(39,54.1] 29 23 4 2 5
Figure 2.8 on page 69 using hmohiv data set with the four age groups created in the previous example.
plot(age.surv, lty=c(6, 1, 4, 3), xlab="Time", ylab="Survival Probability")
legend(40, 1.0, c("Group 1", "Group 2", "Group 3", "Group 4"), lty=c(6, 1, 4, 3))
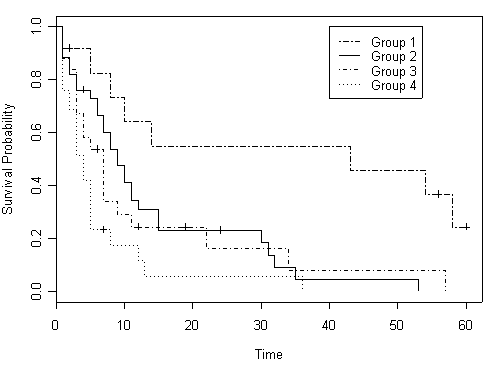
Table 2.14 on page 70, test on survivor curves.
survdiff(Surv(time, censor) ~ agecat, rho=0)
N Observed Expected (O-E)^2/E (O-E)^2/V
agecat=19.9+ thru 29.0 12 8 19.9 7.10608 12.4419
agecat=29.0+ thru 34.0 34 29 29.4 0.00641 0.0117
agecat=34.0+ thru 39.0 25 20 17.8 0.26894 0.3834
agecat=39.0+ thru 54.1 29 23 12.9 7.98170 11.1799
Chisq= 19.9 on 3 degrees of freedom, p= 0.000178
survdiff(Surv(time, censor) ~ agecat, data=hmohiv, rho=1)
N Observed Expected (O-E)^2/E (O-E)^2/V
agecat=19.9+ thru 29.0 12 3.05 8.37 3.3859 7.225
agecat=29.0+ thru 34.0 34 15.11 18.21 0.5267 1.320
agecat=34.0+ thru 39.0 25 12.48 11.48 0.0872 0.172
agecat=39.0+ thru 54.1 29 17.06 9.64 5.7134 10.355
Chisq= 15.4 on 3 degrees of freedom, p= 0.00154
Fig. 2.9 and table 2.16 are not reproduced since we don’t have the data set.
Table 2.17 on page 76 to calculate the Nelson-Aalen estimator of the survivorship function for hmohiv data. The easiest way to get Nelson-Aalen estimator is via cox regression using coxph function.
a<- survfit(coxph(Surv(time,censor)~1), type="aalen")
summary(a)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
1 100 15 0.8607 0.0333 0.7978 0.929
2 83 5 0.8104 0.0382 0.7388 0.889
3 73 10 0.7066 0.0453 0.6233 0.801
4 61 4 0.6618 0.0476 0.5747 0.762
............................................................
54 6 1 0.0897 0.0350 0.0417 0.193
57 4 1 0.0698 0.0324 0.0281 0.173
58 3 1 0.0500 0.0286 0.0163 0.153
With object a we can create Table 2.17 as follows.
h.aalen<-(-log(a$surv))
aalen.est<-cbind(time=a$time, d=a$n.event, n=a$n.risk,
h.aalen, s1=a$surv)
b<-survfit(Surv(time, censor)~1) km.est<-cbind(time=b$time, s2=b$surv) all<-merge(data.frame(aalen.est), data.frame(km.est), by="time") all
time d n h.aalen s1 s2 1 1 15 100 0.1500000 0.86070798 0.85000000 2 2 5 83 0.2102410 0.81038895 0.79879518 3 3 10 73 0.3472273 0.70664471 0.68937118 4 4 4 61 0.4128010 0.66179394 0.64416652 5 5 7 56 0.5378010 0.58403110 0.56364570 6 6 2 49 0.5786174 0.56067304 0.54063975 7 7 6 46 0.7090521 0.49211043 0.47012153 8 8 4 39 0.8116162 0.44413965 0.42190393 9 9 3 35 0.8973305 0.40765643 0.38574074 10 10 3 32 0.9910805 0.37117541 0.34957754 11 11 3 28 1.0982234 0.33346299 0.31212281 12 12 2 25 1.1782234 0.30782514 0.28715298 13 13 1 21 1.2258424 0.29351033 0.27347903 14 14 1 20 1.2758424 0.27919566 0.25980508 15 15 2 19 1.3811056 0.25130056 0.23245718 16 22 1 16 1.4436056 0.23607503 0.21792860 17 30 1 14 1.5150342 0.21980067 0.20236227 18 31 1 13 1.5919572 0.20352687 0.18679595 19 32 1 12 1.6752906 0.18725376 0.17122962 20 34 1 11 1.7661997 0.17098154 0.15566329 21 35 1 10 1.8661997 0.15471050 0.14009696 22 36 1 9 1.9773108 0.13844104 0.12453063 23 43 1 8 2.1023108 0.12217379 0.10896430 24 53 1 7 2.2451679 0.10590975 0.09339797 25 54 1 6 2.4118346 0.08965067 0.07783164 26 57 1 4 2.6618346 0.06982001 0.05837373 27 58 1 3 2.9951679 0.05002823 0.03891582
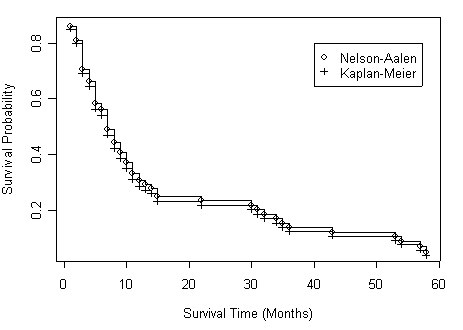
Figure 2.10 on page 77 based on the output from previous example.
plot(all$time, all$s1, type="s", xlab="Survival Time (Months)",
ylab="Survival Probability")
points(all$time, all$s1, pch=1)
lines(all$time, all$s2, type="s")
points(all$time, all$s2, pch=3)
legend(40, .8, c("Nelson-Aalen", "Kaplan-Meier"), pch=c(1, 3))
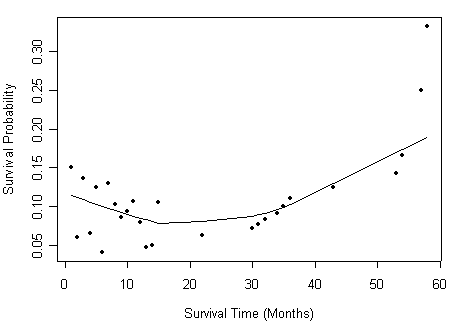
Figure 2.12 on page 82 based on the data set created from previous example.
h2<-all$d/all$n
plot.new()
plot(all$time, h2, type="p", pch=20, xlab="Survival Time (Months)",
ylab="Hazard Ratio")
lines(lowess(all$time, h2,f=.75, iter=5))