The posterior is just the prior times the likelihood.
\[ p(theta | X) = frac{p(theta)p(X|theta)}{p(X)} \]
Example Prior Distributions
Here we briefly cover some example common prior distributions. Distributions are based on a probability density function or PDF for continuous distributions and a probability mass function for discrete distributions. We also try to show what the distributions look like for different values of their parameters.
To make viewing these distributions easier, here is a little function to plot and label them.
fplot <- function(x, params, pdf) { params <- do.call(expand.grid, params) k <- nrow(params) nc <- ceiling(sqrt(k)) nr <- ceiling(k / nc) stopifnot(k <= nc * nr) labeller <- function(params) { style <- paste(paste0(names(params), "=%2.2f"), collapse = ", ") do.call(sprintf, c(fmt = style, params)) } par(mfrow = c(nr, nc)) lapply(1:k, function(i) { y <- do.call(pdf, c(list(x), params[i, ])) plot(x = x, y = y, ylab = "Density", xlab = labeller(params[i, ]), type = "l") }) return(invisible(NULL)) }
The normal distribution has two parameters, (mu) or the location parameter, and (sigma) or the scale parameter.
\[ PDF(x; mu, sigma^2) = frac{1}{sigmasqrt{2pi}}e^{-frac{1}{2}left(frac{x – mu}{sigma}right)^{2}} \]
fplot( x = seq(from = -50, to = 50, by = .1), params = list(mean = c(-10, -5, 5, 10), sd = c(.1, 1, 10, 100)), pdf = dnorm)
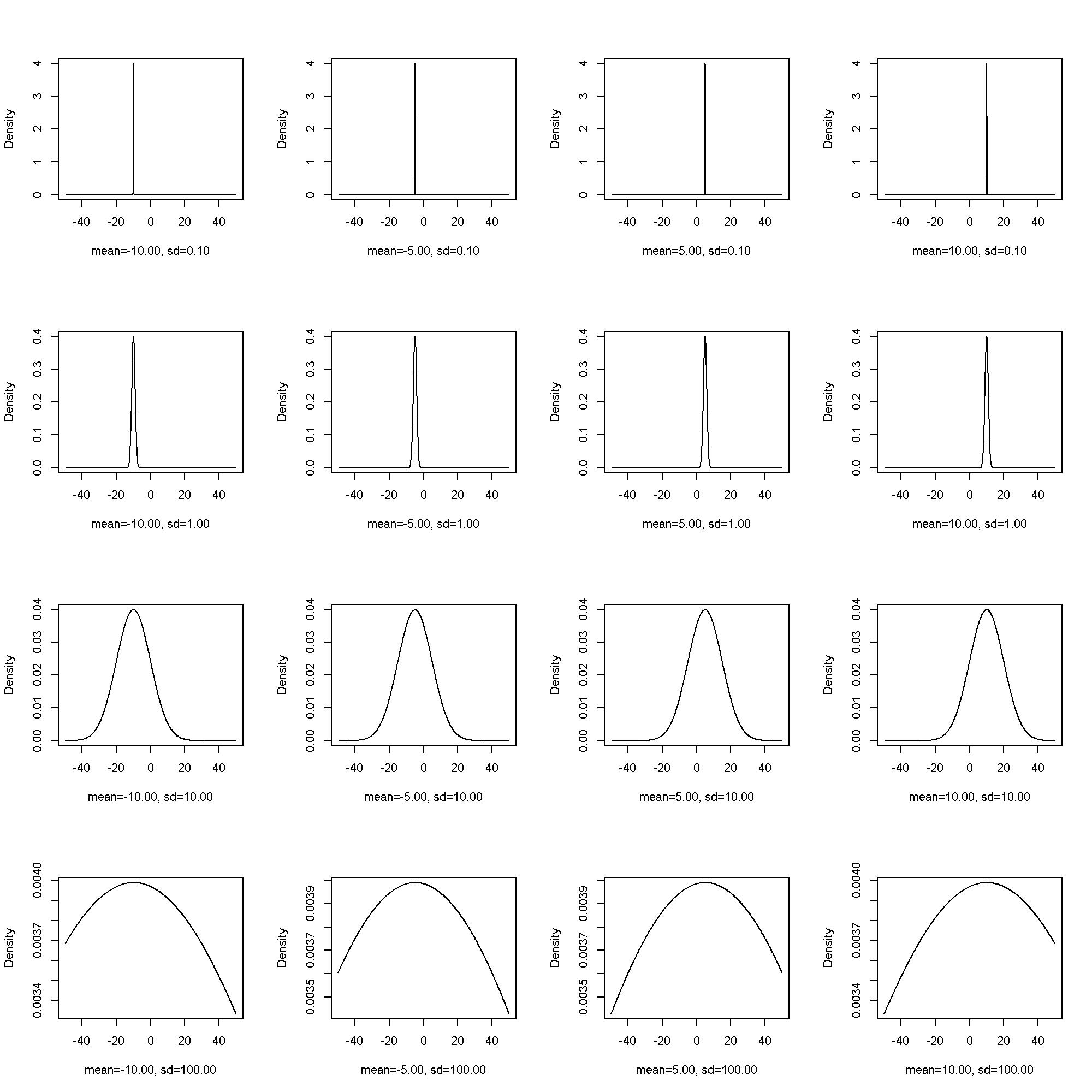
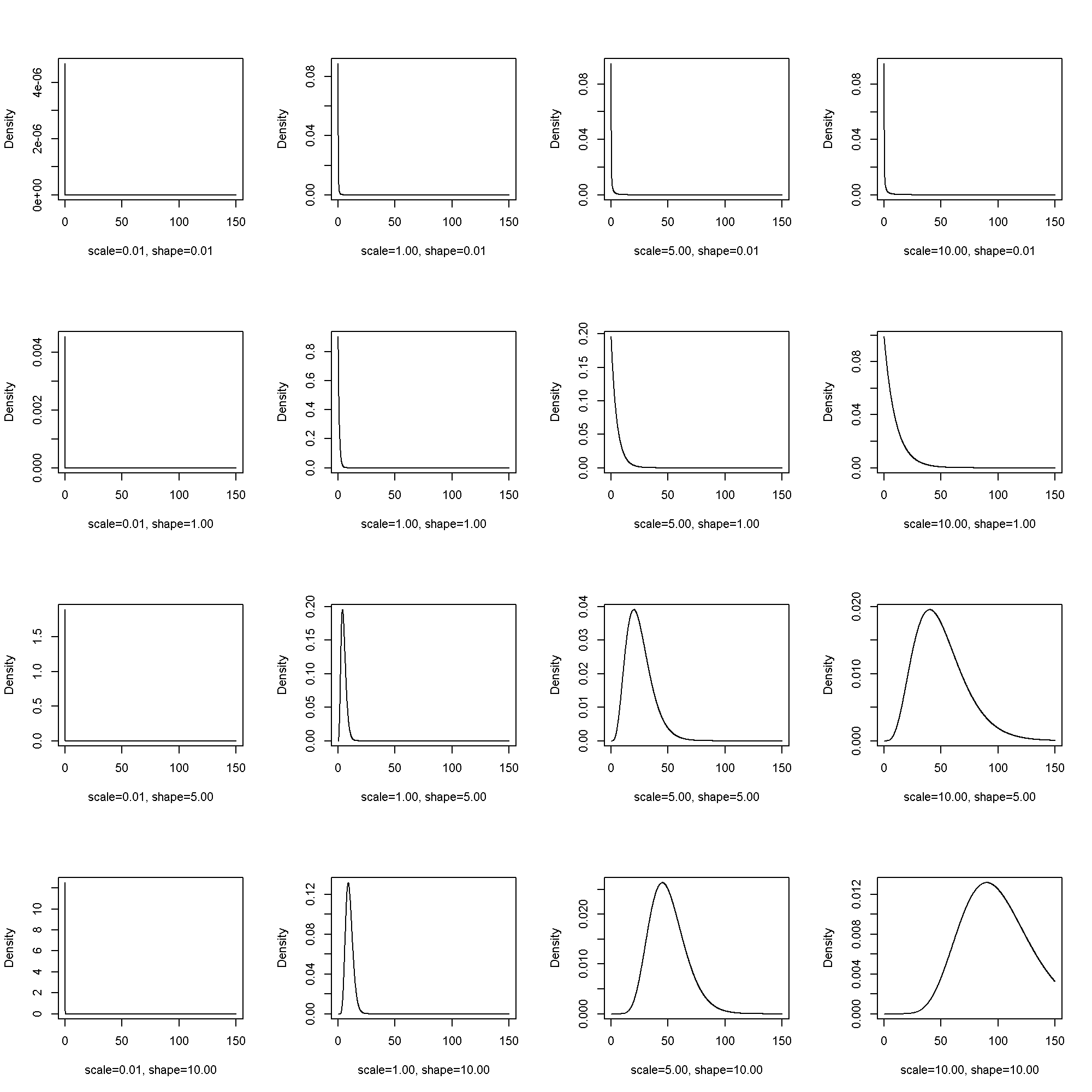
Gamma
The gamma distribution has two parameters, (theta), scale, and (k), shape.
[ PDF(x; theta, k) = frac{1}{Gamma(k)theta^{k}}x^{k – 1}e^{-frac{x}{theta}} ]
Equivalently, the model can be parameterized with (alpha) and (beta).
\[ PDF(x; alpha, beta) = frac{beta^{alpha}}{Gamma(alpha)}x^{alpha – 1}e^{-beta x} \]
fplot( x = seq(from = .1, to = 150, by = .1), params = list(scale = c(.01, 1, 5, 10), shape = c(.01, 1, 5, 10)), pdf = dgamma)
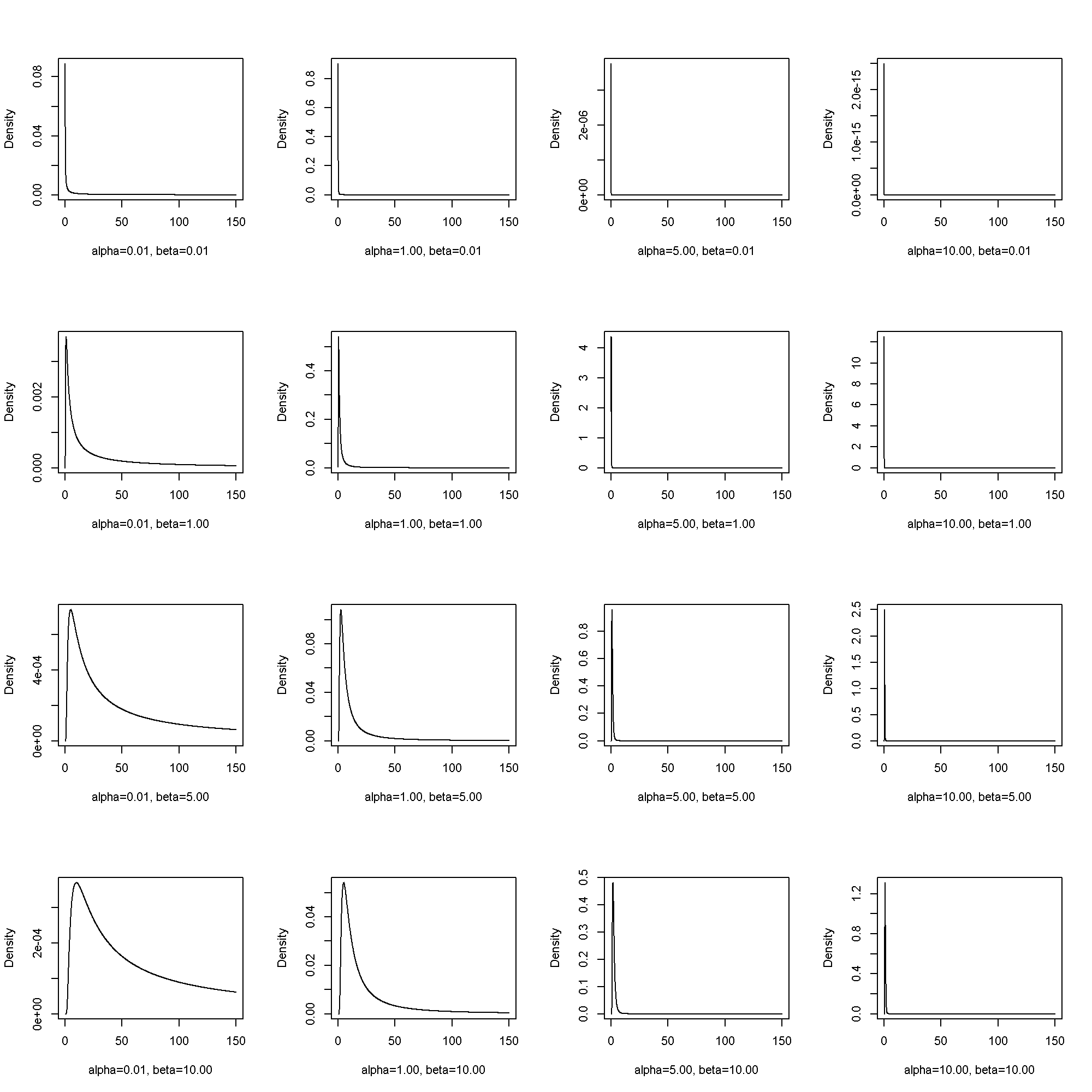
Inverse Gamma
The inverse gamma distribution has two parameters, (alpha) and (beta). [ PDF(x; alpha, beta) = frac{beta^{alpha}}{Gamma(alpha)} x^{-alpha – 1} e^{-frac{beta}{x}} ]
require(pscl)
fplot( x = seq(from = .1, to = 150, by = .1), params = list(alpha = c(.01, 1, 5, 10), beta = c(.01, 1, 5, 10)), pdf = densigamma)
Beta
Coming soon
Inverse Wishart
Coming soon
Continuous Outcomes
The first type of models we will look at have continuous outcomes that are normally distributed. That is our basic model is:
\[ hat{y} sim mathcal{N}(hat{mu}, hat{sigma^2_e}) \]
where
\[ hat{mu} = g(Xhat{beta}) \]
and (g(cdot)) is just the identity function.
Single Level Model
We use MCMCglmm to estimate
the model, which is a sort of canned Bayesian approach. It is in a Bayesian framework,
although you have relatively little control over the priors. All fixed effects use normal priors,
but you can set the mean, mu and variance, V. Here we show a relatively
uninformative prior using a normal with large variance. Thus there is low density across a large
parameter space reflecting our uncertainty or lack of prior specification of plausible parameter
values. Note that we specify the mean and variance for every fixed effect, including the intercept,
if included.
Next, we specify the prior for the residual variance, which is always inverse Wishart.
The small nu parameter again leads to a relatively uninformative prior.
require(foreign)
dat <- read.spss("http://statistics.ats.ucla.edu/stat/data/hsbdemo.sav", to.data.frame=TRUE)
## Warning: C:UsersjwileyAppDataLocalTempRtmpc53SO9filebec68002005: ## Unrecognized record type 7, subtype 18 encountered in system file
dat$cid <- factor(dat$cid) head(dat)
## id female ses schtyp prog read write math science socst ## 1 45 female low public vocation 34 35 41 29 26 ## 2 108 male middle public general 34 33 41 36 36 ## 3 15 male high public vocation 39 39 44 26 42 ## 4 67 male low public vocation 37 37 42 33 32 ## 5 153 male middle public vocation 39 31 40 39 51 ## 6 51 female high public general 42 36 42 31 39 ## honors awards cid ## 1 not enrolled 0 1 ## 2 not enrolled 0 1 ## 3 not enrolled 0 1 ## 4 not enrolled 0 1 ## 5 not enrolled 0 1 ## 6 not enrolled 0 1
require(MCMCglmm)
m1 <- MCMCglmm(write ~ read, data = dat, prior = list( B = list(mu = c(0, 0), V = diag(2) * 1e5), R = list(V = 1, nu = .002)), nitt = 11000, thin = 1, burnin = 1000, verbose=FALSE) autocorr(m1$VCV)
## , , units ## ## units ## Lag 0 1.000000 ## Lag 1 0.003919 ## Lag 5 0.014092 ## Lag 10 0.000891 ## Lag 50 0.008904
autocorr(m1$Sol)
## , , (Intercept) ## ## (Intercept) read ## Lag 0 1.00000 -0.98124 ## Lag 1 0.01039 -0.00793 ## Lag 5 -0.00963 0.00857 ## Lag 10 -0.00484 0.00512 ## Lag 50 -0.00615 0.00405 ## ## , , read ## ## (Intercept) read ## Lag 0 -0.98124 1.00000 ## Lag 1 -0.01100 0.00846 ## Lag 5 0.00931 -0.00846 ## Lag 10 0.00583 -0.00620 ## Lag 50 0.00538 -0.00365
plot(m1$Sol)
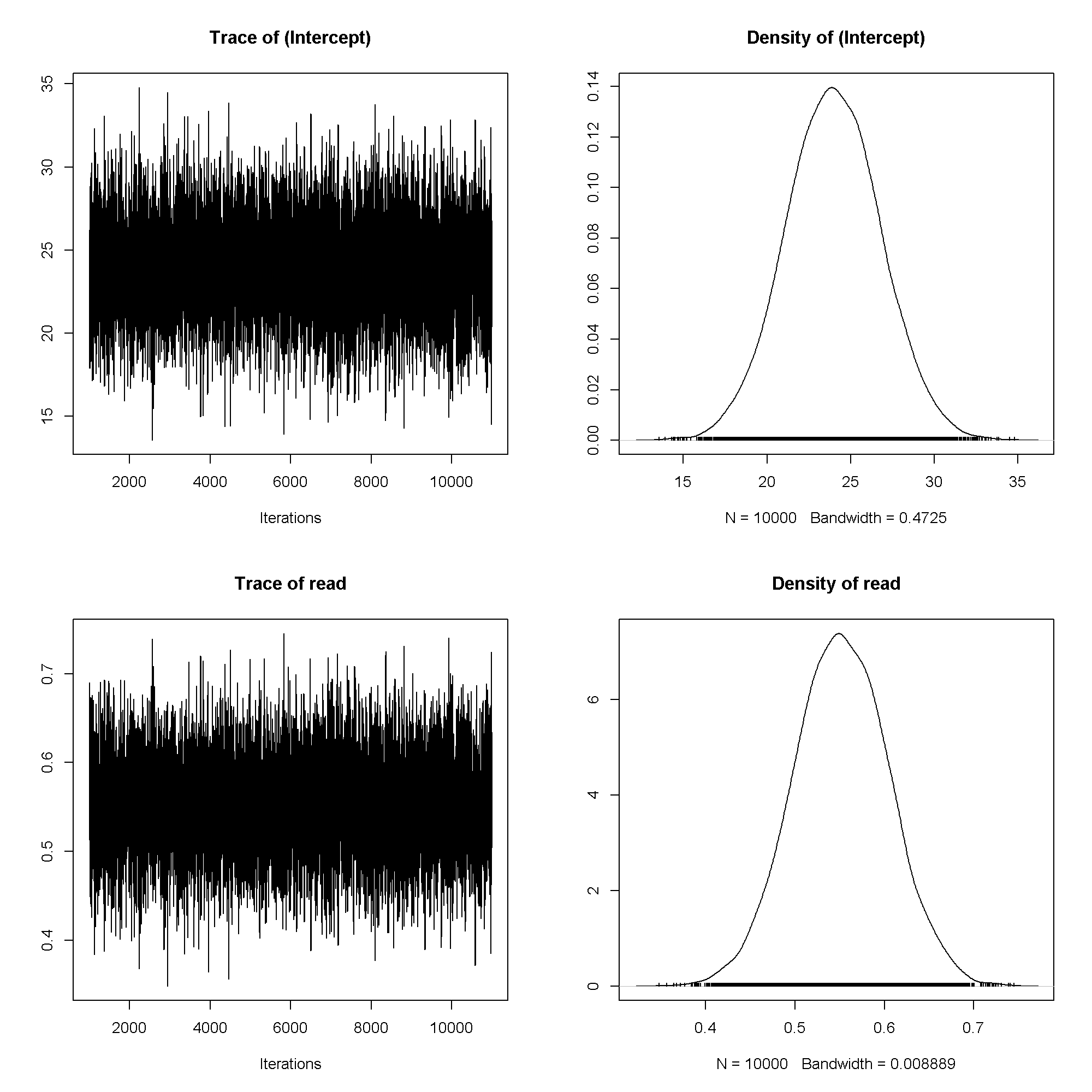
plot(m1$VCV)
summary(m1)
## ## Iterations = 1001:11000 ## Thinning interval = 1 ## Sample size = 10000 ## ## DIC: 1384 ## ## R-structure: ~units ## ## post.mean l-95% CI u-95% CI eff.samp ## units 58.7 47.4 70.7 10000 ## ## Location effects: write ~ read ## ## post.mean l-95% CI u-95% CI eff.samp pMCMC ## (Intercept) 23.963 18.677 29.709 10000
Now we will fit a model with another predictor. Note that female
is a categorical variable. R takes care of dummy coding for us.
m2 <- MCMCglmm(write ~ read + female, data = dat, prior = list( B = list(mu = c(0, 0, 0), V = diag(3) * 1e5), R = list(V = 1, nu = .002)), nitt = 11000, thin = 1, burnin = 1000, verbose=FALSE) autocorr(m2$VCV)
## , , units ## ## units ## Lag 0 1.00000 ## Lag 1 0.01502 ## Lag 5 0.00916 ## Lag 10 -0.00259 ## Lag 50 -0.00375
autocorr(m2$Sol)
## , , (Intercept) ## ## (Intercept) read femalefemale ## Lag 0 1.000000 -0.96224 -0.26010 ## Lag 1 0.003370 -0.00131 -0.00726 ## Lag 5 0.005625 -0.00953 0.01063 ## Lag 10 -0.002035 0.00145 0.01574 ## Lag 50 -0.000812 0.00434 -0.01057 ## ## , , read ## ## (Intercept) read femalefemale ## Lag 0 -0.96224 1.00000 0.06209 ## Lag 1 -0.00622 0.00432 0.00915 ## Lag 5 -0.00822 0.01068 -0.00794 ## Lag 10 0.00220 -0.00217 -0.01475 ## Lag 50 0.00283 -0.00524 0.00605 ## ## , , femalefemale ## ## (Intercept) read femalefemale ## Lag 0 -0.260098 0.062087 1.000000 ## Lag 1 0.010272 -0.011330 -0.000191 ## Lag 5 0.000731 0.003762 -0.015958 ## Lag 10 0.003838 -0.000396 -0.011112 ## Lag 50 -0.001492 0.000743 0.009723
plot(m2$Sol)
plot(m2$VCV)
summary(m2)
## ## Iterations = 1001:11000 ## Thinning interval = 1 ## Sample size = 10000 ## ## DIC: 1358 ## ## R-structure: ~units ## ## post.mean l-95% CI u-95% CI eff.samp ## units 51.4 41.8 62 9703 ## ## Location effects: write ~ read + female ## ## post.mean l-95% CI u-95% CI eff.samp pMCMC ## (Intercept) 20.210 14.895 25.598 10000
Hierarchical Models
Now we are going to fit another normal model, but this one is hierarchical. The model is simple, including only a random intercept. We use more iterations because of the random effects.
m3 <- MCMCglmm(write ~ read + female, data = dat, random = ~ cid, prior = list( B = list(mu = c(0, 0, 0), V = diag(3) * 1e5), R = list(V = 1, nu = .002), G = list( G1 = list(V = 1, nu = .002) )), nitt = 110000, thin = 10, burnin = 10000, verbose=FALSE) autocorr(m3$Sol)
## , , (Intercept) ## ## (Intercept) read femalefemale ## Lag 0 1.00000 -0.85081 -0.20234 ## Lag 10 0.00935 -0.01571 0.00811 ## Lag 50 0.01055 -0.00564 -0.01228 ## Lag 100 -0.00584 0.00133 0.00705 ## Lag 500 -0.01037 0.01408 -0.00635 ## ## , , read ## ## (Intercept) read femalefemale ## Lag 0 -0.85081 1.000000 0.135299 ## Lag 10 -0.00884 0.011146 -0.010516 ## Lag 50 -0.01576 0.013617 0.021852 ## Lag 100 0.00243 0.000506 0.000422 ## Lag 500 0.01300 -0.017286 0.000991 ## ## , , femalefemale ## ## (Intercept) read femalefemale ## Lag 0 -0.20234 0.13530 1.00000 ## Lag 10 0.01182 -0.00835 -0.00980 ## Lag 50 0.00131 -0.00405 0.00439 ## Lag 100 0.01855 -0.01393 -0.01954 ## Lag 500 -0.01508 0.00689 0.00945
autocorr(m3$VCV)
## , , cid ## ## cid units ## Lag 0 1.00000 -0.060213 ## Lag 10 0.00158 -0.004068 ## Lag 50 0.01345 -0.013582 ## Lag 100 -0.00257 -0.000831 ## Lag 500 0.00507 0.014808 ## ## , , units ## ## cid units ## Lag 0 -0.06021 1.000000 ## Lag 10 -0.00166 0.004646 ## Lag 50 -0.00989 -0.000598 ## Lag 100 0.00585 0.002254 ## Lag 500 0.00235 0.013729
plot(m3$Sol)
plot(m3$VCV)
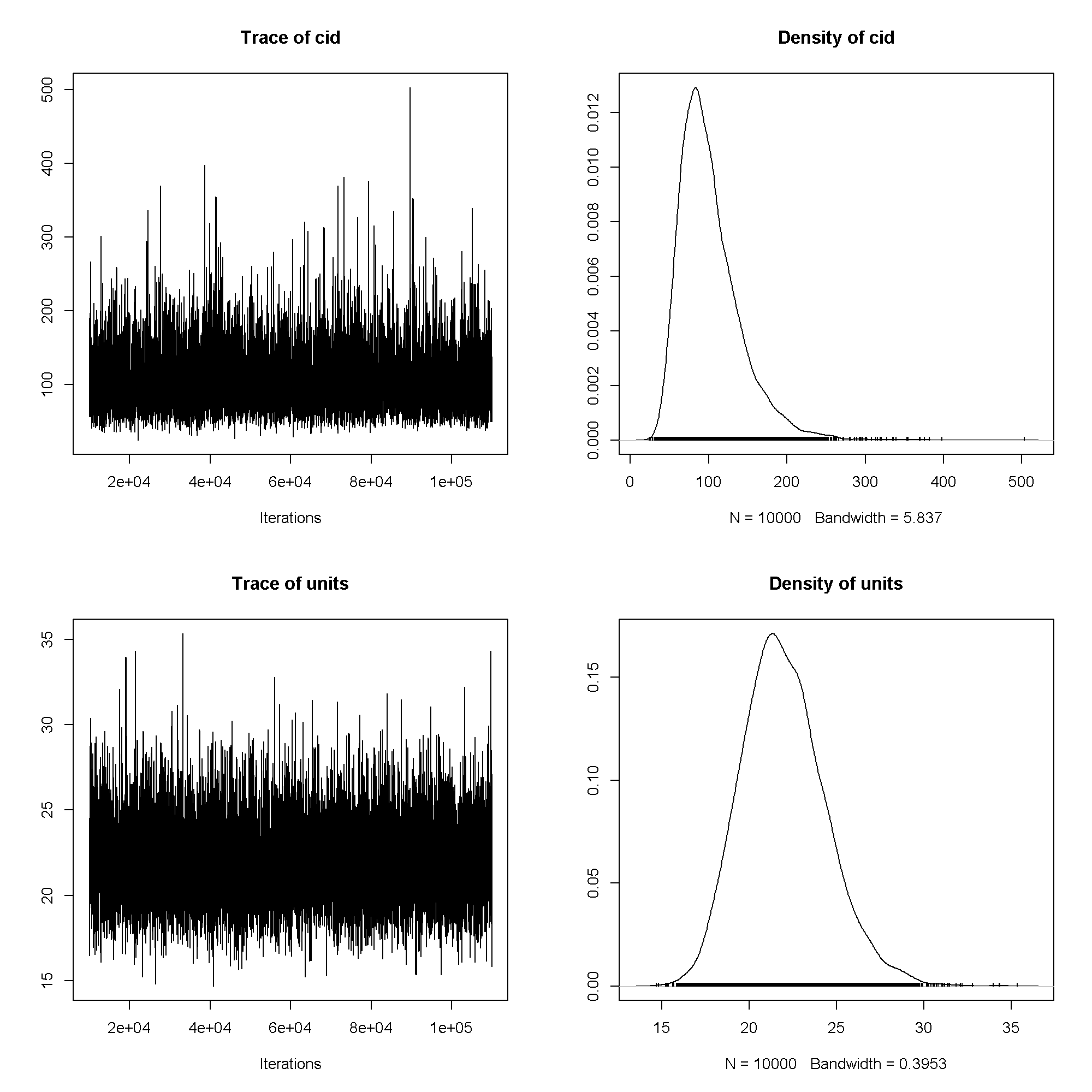
summary(m3)
## ## Iterations = 10001:109991 ## Thinning interval = 10 ## Sample size = 10000 ## ## DIC: 1207 ## ## G-structure: ~cid ## ## post.mean l-95% CI u-95% CI eff.samp ## cid 102 40 179 10000 ## ## R-structure: ~units ## ## post.mean l-95% CI u-95% CI eff.samp ## units 22 17.6 26.8 10000 ## ## Location effects: write ~ read + female ## ## post.mean l-95% CI u-95% CI eff.samp pMCMC ## (Intercept) 60.5278 52.1184 69.1116 10000
Binary Outcomes
For these we fit essentially the same model, but the family is different (binomial) and the link funciton is the logit.
Single Level Model
Because MCMCglmm does not allow you to set zero residual variance
because it makes the MCMC sampling easier. However, to put this on the scale of
typical logistic regressions, we need to use a scaling factor.
# residual variance sigma2 <- 1 # scaling factor k <- sqrt(1 + (((16 * sqrt(3))/(15 * pi))^2) * sigma2) # fit the model m4 <- MCMCglmm(honors ~ read + female, data = dat, family = "categorical", prior = list( B = list(mu = c(0, 0, 0), V = diag(3) * c(1e6, 10, 10)), R = list(V = sigma2, fix = 1)), nitt = 500*2500 + 5000, thin = 500, burnin = 5000, verbose=FALSE) m4$Sol <- m4$Sol/k m4$VCV <- m4$VCV/(k^2) autocorr(m4$Sol)
## , , (Intercept) ## ## (Intercept) read femalefemale ## Lag 0 1.00000 -0.973809 -0.3887 ## Lag 500 0.01087 -0.017710 0.0322 ## Lag 2500 -0.00361 0.000725 0.0122 ## Lag 5000 0.00927 -0.003536 -0.0470 ## Lag 25000 -0.00171 0.009756 -0.0233 ## ## , , read ## ## (Intercept) read femalefemale ## Lag 0 -0.973809 1.00000 0.22484 ## Lag 500 -0.014289 0.02214 -0.03361 ## Lag 2500 -0.000844 0.00160 -0.00286 ## Lag 5000 -0.010716 0.00649 0.04143 ## Lag 25000 0.009233 -0.01377 0.01403 ## ## , , femalefemale ## ## (Intercept) read femalefemale ## Lag 0 -0.388652 0.224845 1.0000 ## Lag 500 0.016230 -0.019627 -0.0152 ## Lag 2500 0.000133 0.004723 -0.0166 ## Lag 5000 -0.000486 -0.005471 0.0312 ## Lag 25000 -0.013980 0.000951 0.0355
plot(m4$Sol)
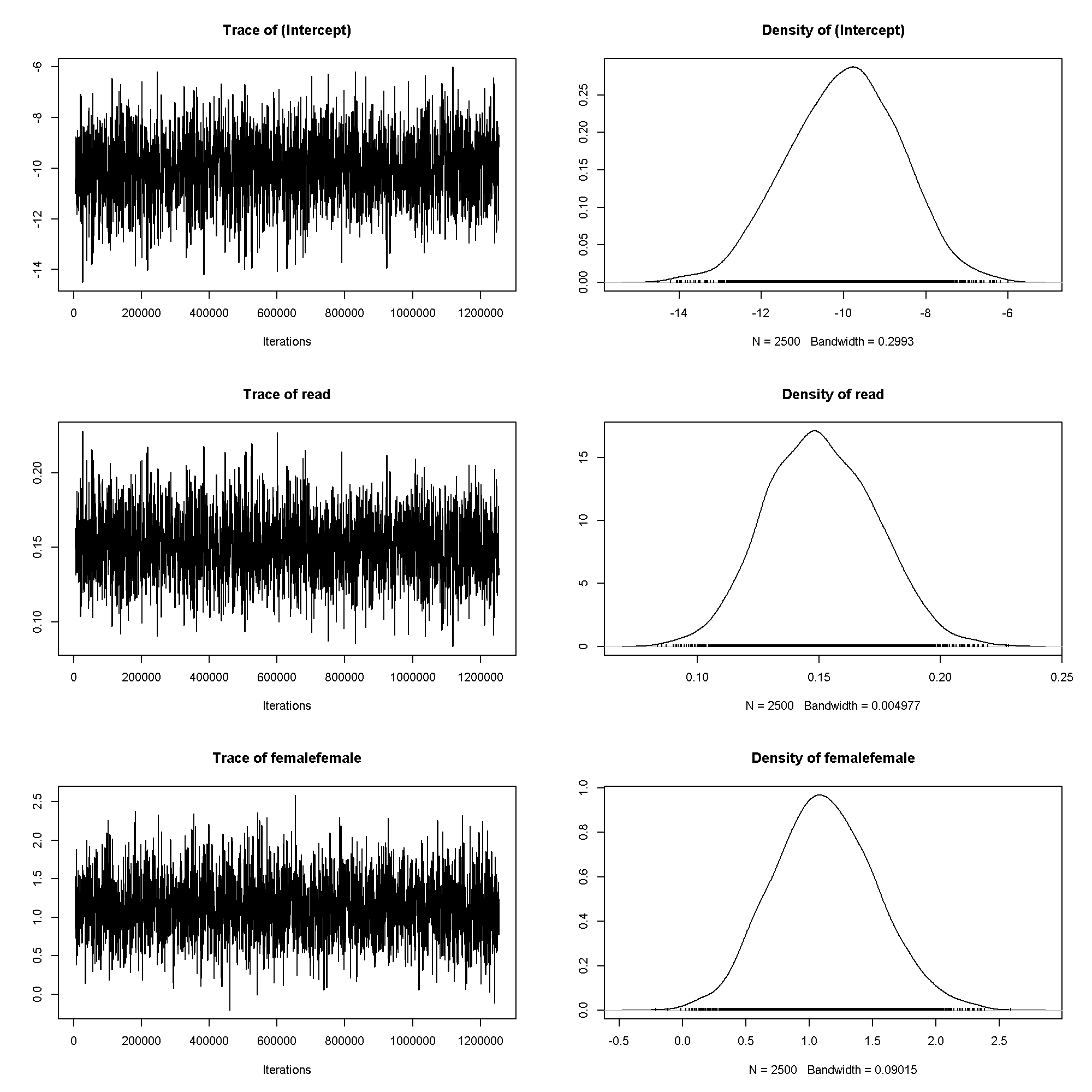
summary(m4)
## ## Iterations = 5001:1254501 ## Thinning interval = 500 ## Sample size = 2500 ## ## DIC: 174 ## ## R-structure: ~units ## ## post.mean l-95% CI u-95% CI eff.samp ## units 0.743 0.743 0.743 0 ## ## Location effects: honors ~ read + female ## ## post.mean l-95% CI u-95% CI eff.samp pMCMC ## (Intercept) -9.990 -12.600 -7.448 2500
Hierarchical Models
start <- proc.time() m5 <- MCMCglmm(honors ~ read + female, data = dat, family = "categorical", random = ~ cid, prior = list( B = list(mu = c(0, 0, 0), V = diag(3) * c(1e6, 10, 10)), R = list(V = sigma2, fix = 1), G = list( G1 = list(V = 1, nu = .002) )), pr=TRUE, pl=TRUE, nitt = 500*5000 + 10000, thin = 500, burnin = 10000, verbose=FALSE) end <- proc.time() # time in minutes (end - start)/60
## user system elapsed ## 7.8442 0.0005 7.8458
m5$Sol <- m5$Sol/k
m5$VCV <- m5$VCV/(k^2)
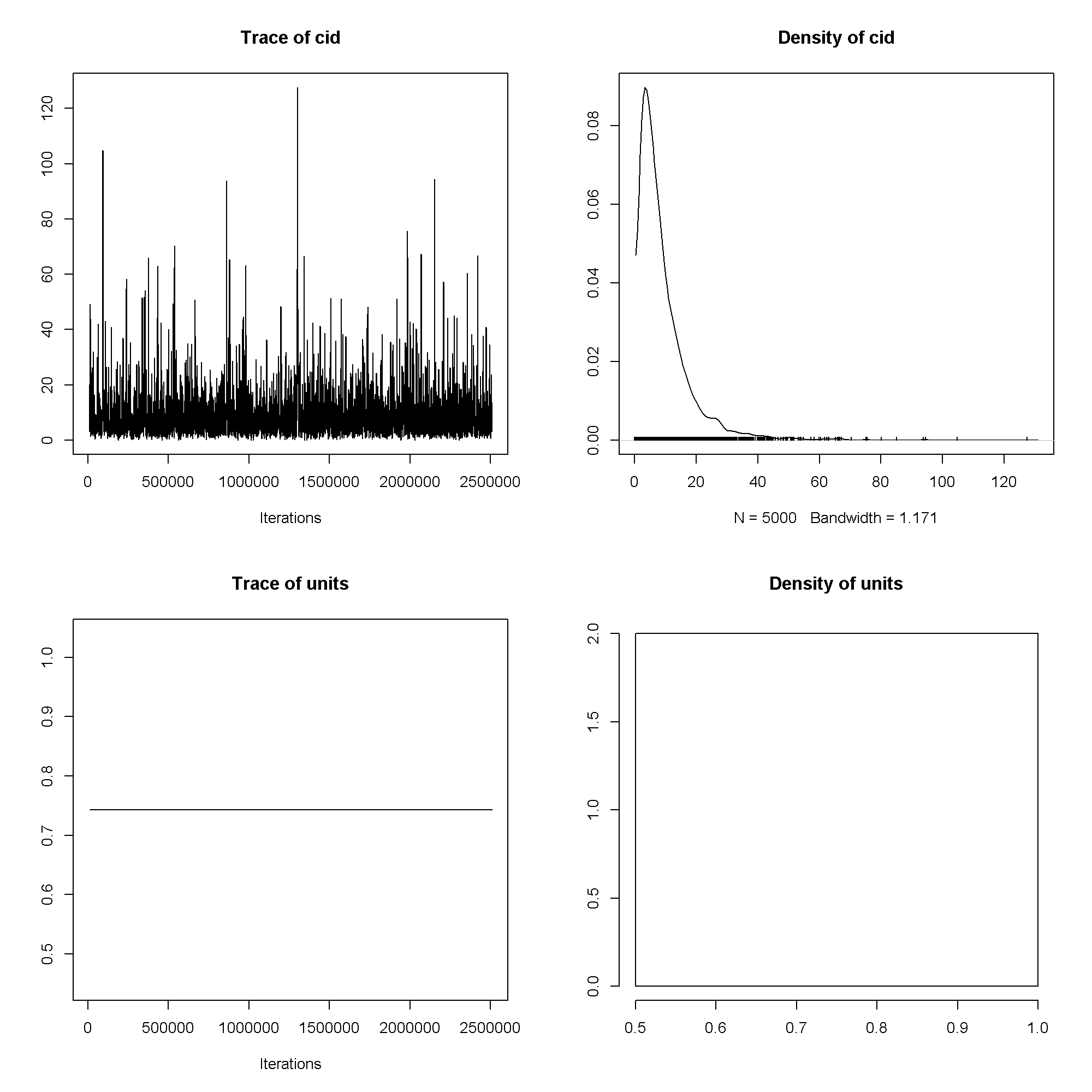
plot(m5$VCV)
plot(m5$Sol[, 1:3])
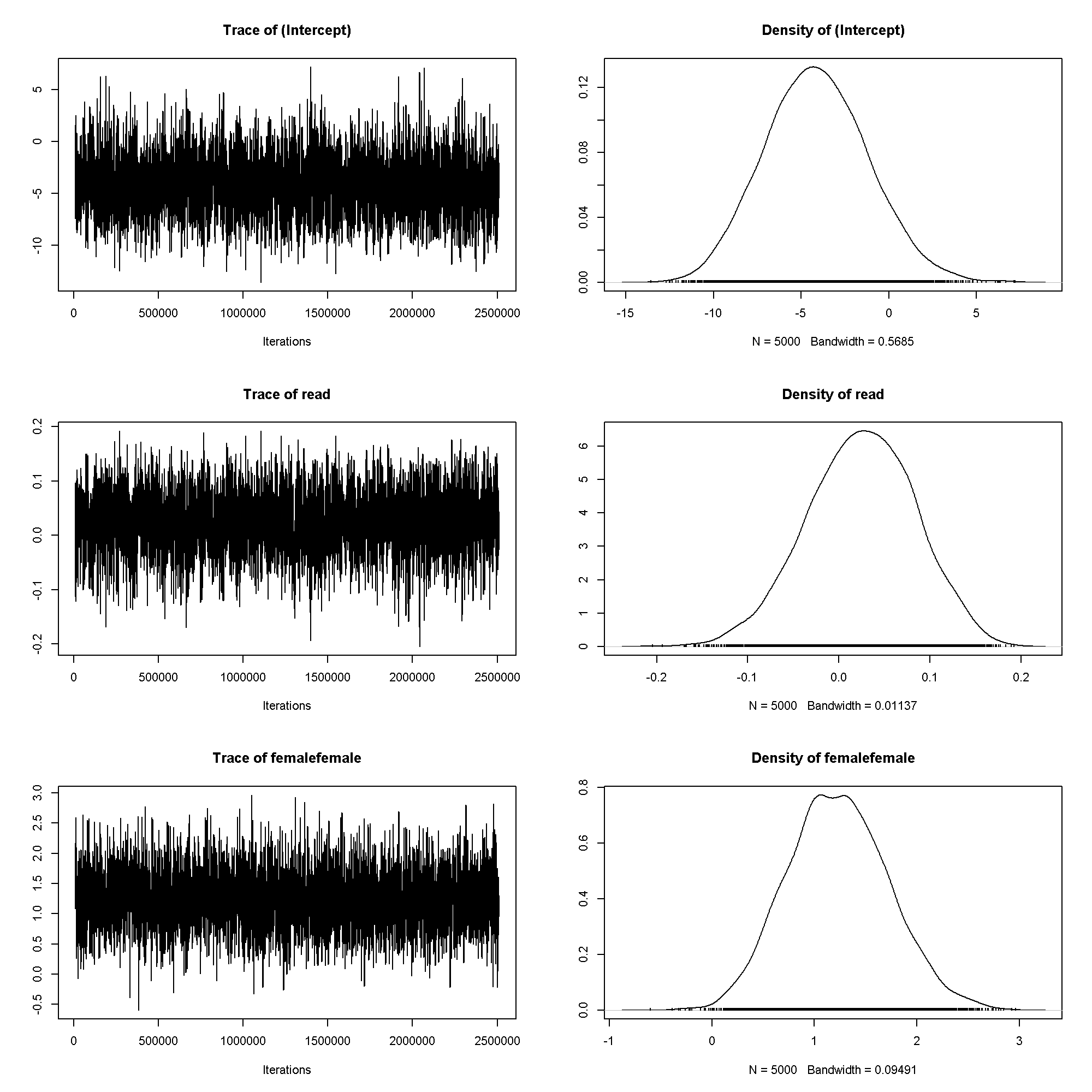
summary(m5)
## ## Iterations = 10001:2509501 ## Thinning interval = 500 ## Sample size = 5000 ## ## DIC: 143 ## ## G-structure: ~cid ## ## post.mean l-95% CI u-95% CI eff.samp ## cid 9.18 0.00244 25.9 1516 ## ## R-structure: ~units ## ## post.mean l-95% CI u-95% CI eff.samp ## units 0.743 0.743 0.743 0 ## ## Location effects: honors ~ read + female ## ## post.mean l-95% CI u-95% CI eff.samp pMCMC ## (Intercept) -4.1265 -10.1146 1.3013 3805 0.1680 ## read 0.0242 -0.0858 0.1420 3045 0.6736 ## femalefemale 1.2305 0.2780 2.1819 4800 0.0068 ** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
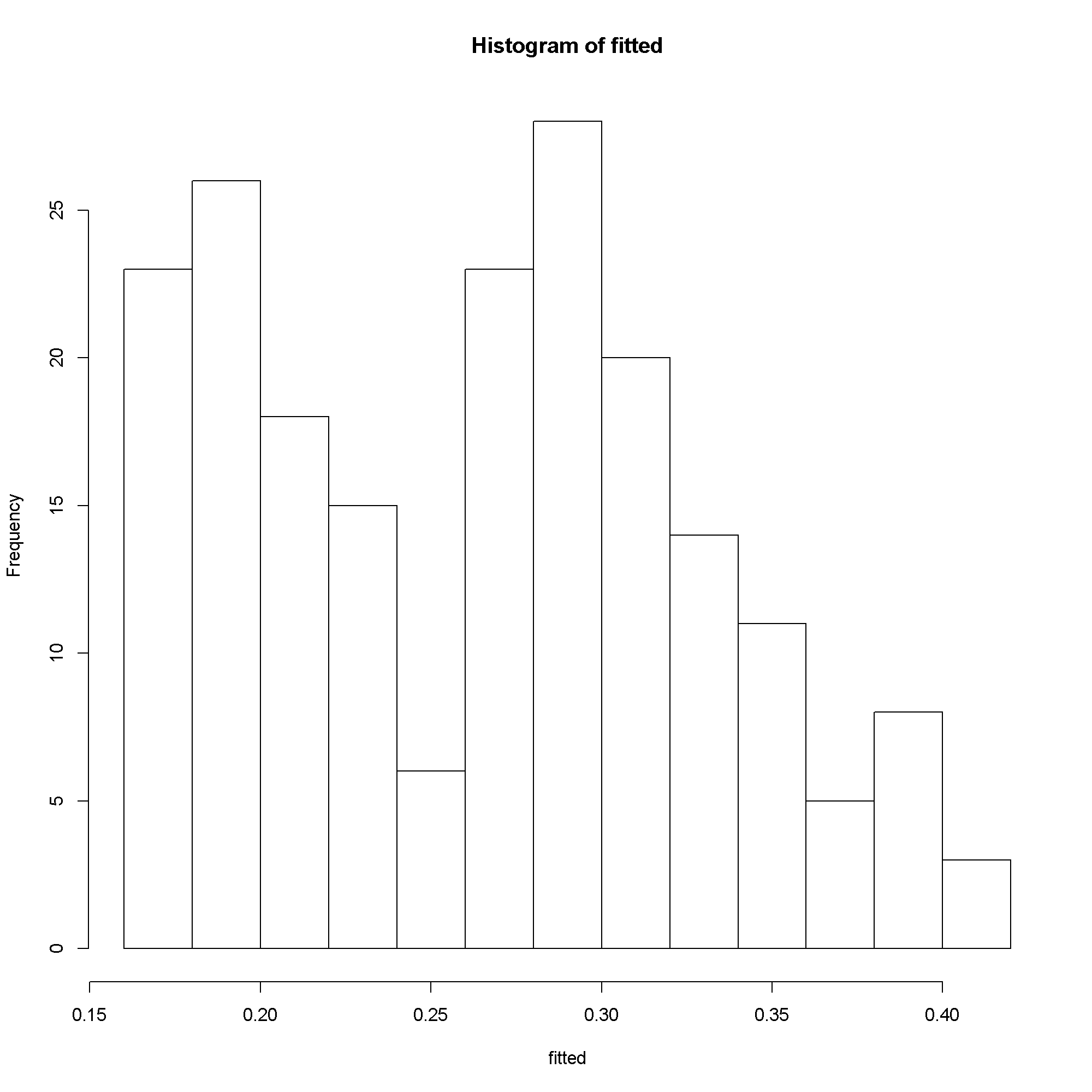
# predicted probabilities fitted <- predict(m5) hist(fitted)
# example using a frequentist approach lme4:::glmer(honors ~ read + female + (1 | cid), data = dat, family = "binomial", nAGQ = 20)
## Generalized linear mixed model fit by the adaptive Gaussian Hermite approximation ## Formula: honors ~ read + female + (1 | cid) ## Data: dat ## AIC BIC logLik deviance ## 167 181 -79.7 159 ## Random effects: ## Groups Name Variance Std.Dev. ## cid (Intercept) 4.44 2.11 ## Number of obs: 200, groups: cid, 20 ## ## Fixed effects: ## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -4.8057 2.1187 -2.27 0.023 * ## read 0.0422 0.0367 1.15 0.251 ## femalefemale 1.2044 0.4894 2.46 0.014 * ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Correlation of Fixed Effects: ## (Intr) read ## read -0.955 ## femalefemal -0.285 0.147
Count Outcomes
m6 <- MCMCglmm(awards ~ read, data = dat, family = "poisson", prior = list( B = list(mu = c(0, 0), V = diag(2) * c(1e8, 1e8)), R = list(V = sigma2, nu = .002)), nitt = 500*2500 + 5000, thin = 500, burnin = 5000, verbose=FALSE) autocorr(m6$Sol)
## , , (Intercept) ## ## (Intercept) read ## Lag 0 1.000000 -0.98186 ## Lag 500 0.000592 0.00699 ## Lag 2500 -0.018182 0.01213 ## Lag 5000 0.003021 -0.00752 ## Lag 25000 -0.001521 0.00619 ## ## , , read ## ## (Intercept) read ## Lag 0 -0.98186 1.000000 ## Lag 500 0.00382 -0.011260 ## Lag 2500 0.02018 -0.014407 ## Lag 5000 0.00498 -0.000221 ## Lag 25000 0.00577 -0.010563
plot(m6$Sol)
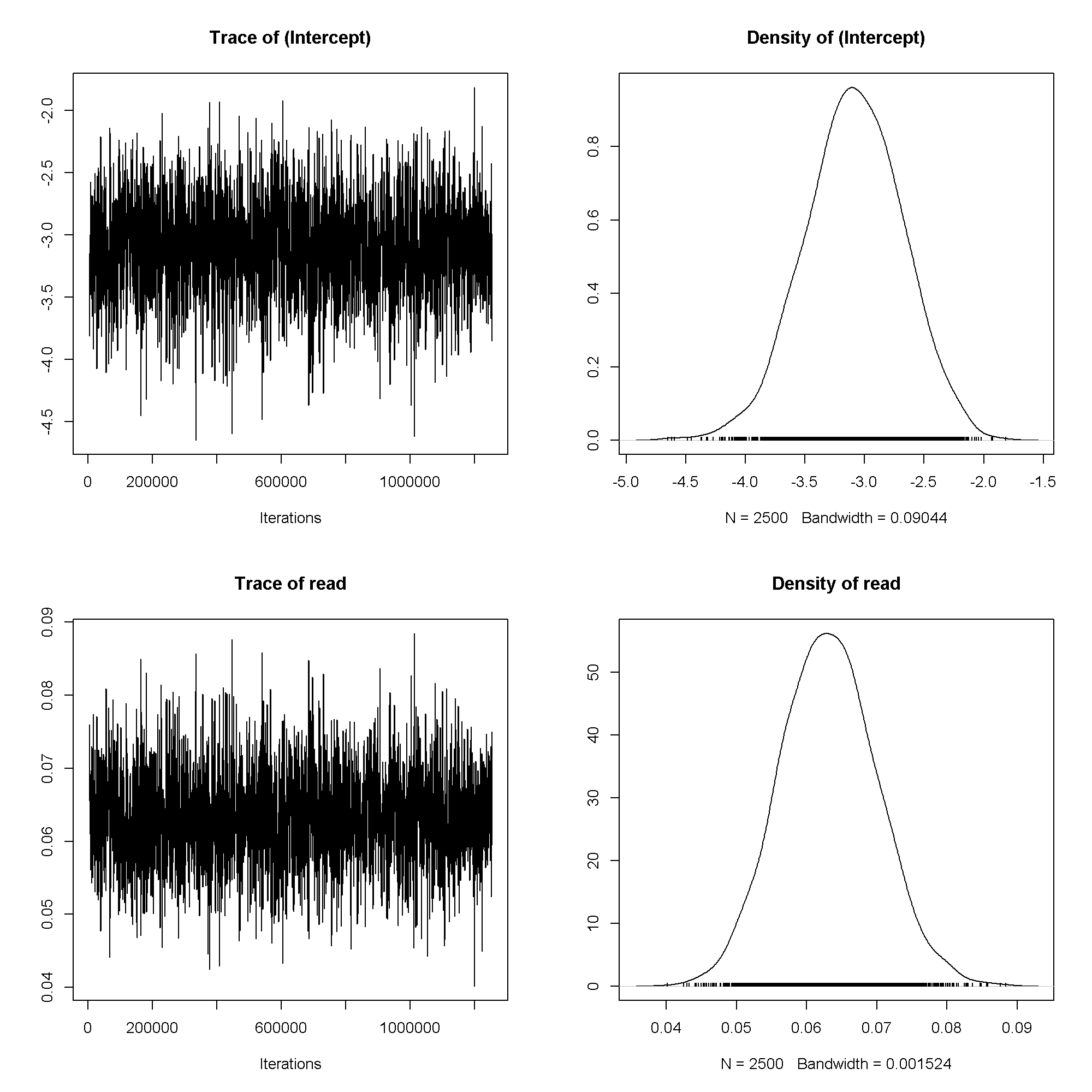
summary(m6)
## ## Iterations = 5001:1254501 ## Thinning interval = 500 ## Sample size = 2500 ## ## DIC: 625 ## ## R-structure: ~units ## ## post.mean l-95% CI u-95% CI eff.samp ## units 0.219 0.0393 0.407 2132 ## ## Location effects: awards ~ read ## ## post.mean l-95% CI u-95% CI eff.samp pMCMC ## (Intercept) -3.0900 -3.8709 -2.2905 2500
