Purpose
This seminar is the third and final part in a series of workshops on latent variable models. The first seminar introduces the confirmatory factor analysis model, and discusses model identification, degrees of freedom and model fit.
Confirmatory Factor Analysis (CFA) in R with lavaan
The second seminar explores structural equation models which is an umbrella term that encompass linear regression, multivariate regression, path analysis, CFA and structural regression.
Introduction to Structural Equation Modeling (SEM) in R with lavaan
The purpose of this third seminar is to introduce 1) latent growth modeling and 2) measurement invariance in CFA. It is best to familiarize yourself with the two previous seminars before proceeding. A rudimentary knowledge of linear regression and hierarchical linear models is helpful to understanding some of the material in this seminar. The assumption is that all variables are continuous and normally distributed.
- This seminar focuses on extensions of confirmatory factor analysis. For exploratory factor analysis (EFA), please refer to A Practical Introduction to Factor Analysis: Exploratory Factor Analysis.
Outline
Proceed through the seminar in order or click on the hyperlinks below to go to a particular section:
- Specifying the latent growth model in lavaan
- Interpreting the parameters in an LGM
- Ordinal versus measured time in an LGM
- Equivalence of the LGM to the hierarchical linear model (HLM)
- Adding a predictor to the latent growth model (LGM)
- Technical notes about LGMs with a predictor
- Understanding the LGM with a predictor
- Equivalence of the LGM to an HLM with a time predictor
- Single group CFA
- Multigroup CFA
- Configural invariance
- Metric (Weak) invariance
- Variance standardization in metric invariance
- Scalar (Strong) invariance
- Residual (Strict) invariance
- Model fit comparisons of invariance models
- Partial invariance
Requirements
Before beginning the seminar, please make sure you have R and RStudio installed. Also install the following R packages:
install.packages("lavaan", dependencies=TRUE)
install.packages("lme4", dependencies=TRUE)
Once you’ve installed the two packages, you can load them via the following commands:
library(lavaan) library(lme4)
Download the complete R code and data files
You may download the complete R code here: lgm20210818.r
After clicking on the link, you can copy and paste the entire code into R or RStudio.
PowerPoint slides for the seminar on August 16, 2021 are available for download lgm_20210816d.pptx
The seminar uses the following data sets available for download
- Hox Chapter 5 GPA dataset in wide (multivariate) format gpa_wide.csv
- Hox Chapter 5 GPA dataset in long (univariate) format gpa_long.csv
- High School and Beyond sample dataset hsbdemo.csv
Introduction
From reading the first two seminars Confirmatory Factor Analysis (CFA) in R with lavaan and Introduction to Structural Equation Modeling (SEM) in R with lavaan, you are familiar with the fundamental mechanics of a CFA. The goal of the seminar is to introduce two intermediate topics in CFA/SEM, most notably a) latent growth modeling and b) measurement invariance. These topics extend the capacities of a simple CFA models to allow researchers to investigate longitudinal trends or group differences in measurement.
The latent growth model (LGM) extends CFA to the analysis of items across time. LGMs are used in longitudinal studies where the researcher is interested in modeling and assessing growth trajectories. For example, suppose the researcher wants to model the trajectory of depressive symptoms among a cohort of breast cancer patients post-mastectomy. The hope is that this trajectory goes down over time, as the patient learns to recover and heal from the trauma of their breast cancer diagnosis.
A second distinctive topic in CFA centers around multigroup CFA and measurement invariance. The purpose of measurement invariance is to assess the plausibility of stratifying the CFA model into distinctive units of analysis. For example, suppose we are again measuring the construct of depression (in a cross-section of time) among breast cancer patients, but stratified by those who received surgery versus those who did not. To be able to compare the severity of depression across these two groups of patients, depression must be measured similarly for surgery and non-surgery patients. Measurement similarity, or more precisely, measurement invariance must be achieved before depression can be compared between or among groups.
Finally, beyond a simple understanding of the concepts of LGM and measurement invariance, the primary learning objective of this seminar is to be able to implement these models in lavaan with a modicum of technical rigor. For both LGM and measurement invariance models, we will introduce its
- matrix formulation
- path diagram
lavaansyntax- interpretation of parameters and output
By the end of this seminar, you should be able to 1) implement a latent growth model (LGM) and identify its parallels to hierarchical linear models (HLM), and 2) assess the measurement invariance of a simple CFA model.
Loading the dataset
The dataset can be loaded directly from our servers from within R, provided there is an internet connection:
widedat <- read.csv("https://stats.idre.ucla.edu/wp-content/uploads/2021/08/gpa_wide.csv")
longdat <- read.csv("https://stats.idre.ucla.edu/wp-content/uploads/2021/08/gpa_long.csv")
hsbdemo <- read.csv("https://stats.idre.ucla.edu/wp-content/uploads/2021/07/hsbdemo.csv", stringsAsFactors=TRUE)
For the hsbdemo dataset, make sure to specify the stringsAsFactors=TRUE option to make sure that the variables are imported as numeric factors rather than as character variables.
lavaan syntax cheatsheet
Before diving into the content, let us remind ourselves some of the most frequently used sets of syntax in lavaan
~predict, used for regression of observed outcome to observed predictors=~indicator, used for latent variable to observed indicator in factor analysis measurement models~~covariance~1intercept or mean (e.g.,q01 ~ 1estimates the mean of variableq01)1*fixes parameter or loading to oneNA*frees parameter or loading (useful to override default marker method)a*labels the parameter ‘a’, used for model constraintsc(a,b)*specifically for multigroup models, see note below
Special mention of c(a,b)* is warranted, which is specifically used for multigroup CFA or SEM models that is unique to lavaan. The c(a,b) specifies a two-group model with labels a for the first group and b for the second group. For three groups, the syntax c(a,b,c) is an equivalent specification. If the parameters are free to begin with, different labels signify different free parameters, and the same label specifies a free parameters that is constrained to be the same across groups. For example, supposing we are estimating a free parameter, c(a,a)*x1 labels the loading for the item corresponding to $x_1$ ‘a’, and the repeated ‘a’ means to constrain the loadings to be equal across the two groups. However, this is not true if the loadings are constrained to begin with (e.g., constrained by marker method), as we will see in the section Partial invariance. For any parameter, specifying a numeric value means to fix the parameters at that value. For example c(1,1)*x1 means to fix the loadings of $x_1$ on that factor to be 1.
Quiz
True or false. c(2,2,2,2)*x1 fixes the loadings of the item x1 to be 2 for all four groups.
Answer: True.
True or false. c(a,a,1)*x1 fixes the loadings of the two groups to 1.
Answer: False. There are three groups specified, the first two groups are constrained to have equal loadings
The latent growth model (LGM)
Latent growth models (LGMs) are a special class of confirmatory factor analysis models used specifically to model trajectories over time. These trajectories in most cases are linear, but can encompass other trajectories such as a quadratic slope or even slopes that are freely varying. Since this is an introductory seminar we will only explore linear trajectories. For those familiar with the more modern hierarchical linear model, we will emphasize the equivalence of these LGM and HLM through some slight modifications to the dataset and parameter constraints.
To motivate the LGM, we introduce a modified dataset from Chapter 5 of Hox’s Multilevel Analysis: Techniques and Applications, which measures student gender and GPA across five semesters. The goal of our current LGM is to assess the linear trajectory of GPA, with the question being, does the average student GPA in a particular school go up or down over time?
You can think of LGMs as an extension of the CFA model a mean structure, meaning the intercepts ($\tau$’s) are freely estimated. The inclusion of mean structure implies that we cannot supply only the sample variance-covariance matrix, but instead need observation (student) level data. Another stipulation of LGMs is that the dataset be structured in wide format, which means that each column represents the outcome or dependent variable at a specific timepoint. An assumption is that each observation or row must be independent of another, however columns indicating outcomes are time dependent. This is unlike HLMs which are structured long, where a single subject can have multiple observations down the rows, and there is only one column for the dependent variable (in univariate HLMs). Another name for this data setup is called the multivariate approach, in contrast to the univariate approach. Now that we know what the dataset should look like, our first task is to import the dataset gpa_wide.csv. The first three students in the dataset are shown below. Note that females are coded sex=1 and males are coded sex=0.
student gpa0 gpa1 gpa2 gpa3 gpa4 sex 1 2.3 2.1 3 3 3 1 2 2.2 2.5 2.6 2.6 3 0 3 2.4 2.9 3 2.8 3.3 1
As we can see, the first female student’s GPA is recorded to be 2.3, 2.1, 3.0, 3.0, 3.0 across 5 semesters; which suggests this student is has a positive trajectory. The goal of the LGM is to see the average trajectory across all students.
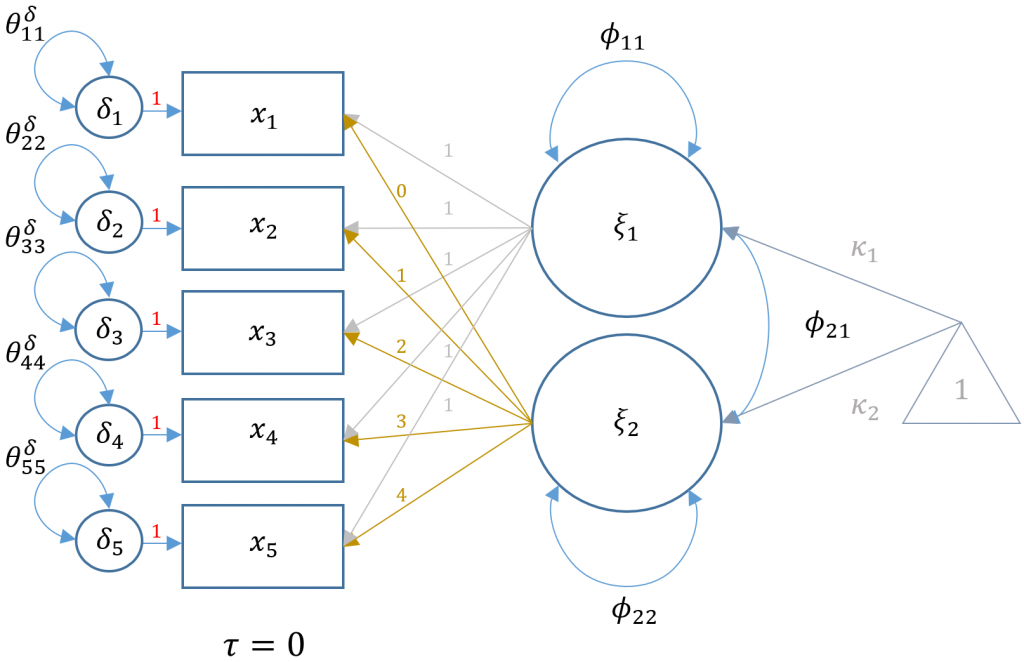
We mentioned previously that LGMs are a special case of CFA, and more specifically it is a two-factor CFA where the loadings are fixed to particular values. First, $t$ number of outcomes make up the x-side indicators for both the intercept and linear slope factor. Second, the loadings for the intercept factor are all fixed to 1 and the loadings for the linear slope factor can be any ordered progression. Most commonly, the first loading of the slope factor is fixed to 0 and the progression proceeds ordinally in increments of 1. More rigorously,
$\lambda_{t} = i$ for $i = 0, 1, 2,…$.
The benefit of starting at $0$ is that the mean of the intercept factor is interpreted as the mean of the first timepoint. A one-unit increase in time is interpreted as an increase in the predicted outcome for a fixed time interval increase. For example, if time is measured at 0, 3, 6, 9, and 12 months (the length of a semester), an ordinal increase of one unit leads to an increase of 3 months. The LGM can be described in CFA matrix notation as:
$$ x_i = \Lambda \xi + \delta_i $$
where in our case $\Lambda$ is a $5 \times 2$ matrix of fixed loadings for the intercept and slope, $\xi$ is a $2 \times 1$ vector of the latent intercept and slope with latent means $\kappa_{1}$ and $\kappa_{2}$. The $5 \times 1$ vector of residuals is defined by $\delta$. Recall from the seminar Introduction to Structural Equation Modeling (SEM) in R with lavaan that these are x-side indicators since the latent factor to which it belongs is exogenous. Unlike traditional CFA however, the $\Lambda$ matrix is completely fixed and for this particular model:
$$ \Lambda = \begin{pmatrix} 1 & 0 \\ 1 & 1 \\ 1 & 2 \\ 1 & 3 \\ 1 & 4 \\ \end{pmatrix} $$
Here is a path diagram representing our particular LGM:
Multiplying out the equation above, the five equations for each time point defined for a person $i$ and timepoint $t$ is:
$$ x_{it} = \tau_i + (1)\xi_1 + (t)\xi_2 + \delta_{it} $$
for \(t={0,1,2,3,4}\). Note that the observed intercepts are constrained to be zero, so that $\tau_i = 0$.
Equivalently, the equation above can be spelled out with the corresponding five equations (dropping the index for subject $i$ for simplicity):
$$\begin{eqnarray} x_{1} & = & 0 + (1)\xi_{1} + (0)\xi_{2} + \delta_{1} \\ x_{2} & = & 0 + (1)\xi_{1} + (1)\xi_{2} + \delta_{2} \\ x_{3} & = & 0 + (1)\xi_{1} + (2)\xi_{2} + \delta_{3} \\ x_{4} & = & 0 + (1)\xi_{1} + (3)\xi_{2} + \delta_{4} \\ x_{5} & = & 0 + (1)\xi_{1} + (4)\xi_{2} + \delta_{5} \end{eqnarray} $$
where the (symmetric) variance covariance matrix of the latent intercept and slope is defined as:
$$ \mathbf{\Phi} = \begin{bmatrix} \phi_{11} & \\ \phi_{21} & \phi_{22} \end{bmatrix} $$
where $\phi_{11}$ is the variance of the latent intercept, $\phi_{22}$ is the variance of the latent slope and $\phi_{21}$ is the covariance of the intercept and slope. Although not specified in the model, another requirement is that the latent means or $\kappa_1, \kappa_2$ be freely estimated.
Unlike traditional CFA models where the interpretation focuses on the loadings (i.e., $\lambda$’s), the loadings are fixed in latent growth models which implies that the focus is on the latent intercept and linear slope factors. First, note that the indicators are the outcomes measured at each timepoint and that the arrows from the factors point leftwards. In traditional LISREL SEM convention (see Introduction to Structural Equation Modeling (SEM) in R with lavaan), this implies that this is an x-side model. As shown in the path diagram above, the population parameters $\kappa_1,\kappa_2$ correspond to the latent intercept and linear slope means, and $\phi_{11},\phi_{22}$ and $\phi_{12}$ are their respective variances and covariance. Since we are estimating these parameters with sample data, the output from lavaan will have corresponding hat symbols to denote sample estimates (e.g., $\hat{\kappa}_1$).
Specifying the latent growth model in lavaan
The easiest way to specify an LGM in lavaan is to use the growth() function, which is a wrapper function for the lavaan() function that automatically specifies fixed and free parameters for the latent growth model. This avoids having to manually a) constrain the observed intercepts to zero ($\tau_i = 0$ for all $i=0,1,…,T$ where $T$ is the final timepoint) and b) freely estimate the latent means $\kappa_1, \kappa_2$.
m1 <- 'i =~ 1*gpa0 + 1*gpa1 + 1*gpa2 + 1*gpa3 + 1*gpa4
s =~ 0*gpa0 + 1*gpa1 + 2*gpa2 + 3*gpa3 + 4*gpa4'
fit_m1 <- growth(m1, data=widedat)
summary(fit_m1)
The output is as follows
lavaan 0.6-8 ended normally after 62 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 10
Number of observations 200
Model Test User Model:
Test statistic 12.202
Degrees of freedom 10
P-value (Chi-square) 0.272
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
i =~
gpa0 1.000
gpa1 1.000
gpa2 1.000
gpa3 1.000
gpa4 1.000
s =~
gpa0 0.000
gpa1 1.000
gpa2 2.000
gpa3 3.000
gpa4 4.000
Covariances:
Estimate Std.Err z-value P(>|z|)
i ~~
s -0.000 0.002 -0.073 0.942
Intercepts:
Estimate Std.Err z-value P(>|z|)
.gpa0 0.000
.gpa1 0.000
.gpa2 0.000
.gpa3 0.000
.gpa4 0.000
i 2.602 0.018 140.832 0.000
s 0.104 0.006 16.444 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.gpa0 0.069 0.009 7.263 0.000
.gpa1 0.068 0.008 8.628 0.000
.gpa2 0.056 0.006 9.195 0.000
.gpa3 0.036 0.005 7.997 0.000
.gpa4 -0.001 0.005 -0.121 0.903
i 0.034 0.007 4.577 0.000
s 0.006 0.001 5.880 0.000
When you run this model you will notice the following warning.
Warning message: In lav_object_post_check(object) : lavaan WARNING: some estimated ov variances are negative
This is due to the fact that one of the residual variances .gpa4 is negative (i.e., $\hat{\theta}^{\delta}_{44}=-0.001$); a condition known as a Heywood case. Recall that variances involve the sum of squares, which can never be negative. Although there are many causes and solutions to the Heywood case which we will not cover, in the sections below, we will discover a method of removing this warning. In the following section we will interpret the estimated parameters from the output.
Interpreting the parameters in an LGM
Looking at the output above, $\hat{\kappa}_1=2.602$, $\hat{\kappa}_2=0.104$ which means that the predicted GPA in the first semester (i.e., $t=0$) is $2.6$ and for every sequential semester GPA is expected to go up by $0.1$ points. The parameters $\hat{\phi}_{11}=0.034$ and $\hat{\phi}_{22}=0.006$ represents the variances of the intercept and slope across students respectively. Taking the square root of the variance gives us the standard deviation and assuming normality, a 95% plausible value ranges (not confidence intervals, see p.78 of Raudenbush and Bryk) for mean GPA across students is $2.602 \pm 1.96*\sqrt{0.034} = (2.24, 2.96)$ and for the slope is $0.104 \pm 1.96*\sqrt{0.006}=(-0.048,0.256)$ (see Raudenbush and Bryk, p.77-78 for more information). Finally, the estimated covariance or $\hat{\phi}_{21}=0$ which implies that there is no covariance between the intercept and slope. If the effect were positive, we could say that there is a positive relationship between the intercept and slope – the higher the starting value of GPA, the stronger the increase in GPA over time. A negative covariance of intercept and slope would imply that the higher the starting GPA, the weaker the increase in GPA.
Quiz
True or false. In a latent growth model, the observed intercepts are constrained to be zero but the latent intercepts are unconstrained to be free.
Answer: True.
True or false. Suppose the mean of the slope were positive. A positive covariance between the intercept and slope means that for lower values of the starting GPA, the weaker the linear increase in GPA over time.
Answer: True. For positive slopes, a positive covariance means that higher values of the intercept correspond with higher (more positive) slopes and lower values of the intercept correspond with weaker (less positive) slopes.
Ordinal versus measured time in an LGM
There are many ways to specify the fixed loadings for the slope factor depending on how time is modeled. The preceding specification assumed that time is measured ordinally (in increments of semester), regardless of the actual measured time. In other situations, it may be more beneficial to use measured time, such as for a study design where assessments are implemented at baseline, 3-, 6-, 9-, and 12-month follow-up. In this case, the loadings may be fixed at 0, 3, 6, 9 and 12, corresponding to the actual time of assessment. The choice of using ordinal versus measured time does not change the Number of model parameters or the Degrees of freedom, however the mean of the intercept and slope factors may differ and the interpretation of these terms will change as a result.
m2 <- 'i =~ 1*gpa0 + 1*gpa1 + 1*gpa2 + 1*gpa3 + 1*gpa4
s =~ 0*gpa0 + 3*gpa1 + 6*gpa2 + 9*gpa3 + 12*gpa4'
fit_m2 <- growth(m2, data=widedat)
summary(fit_m2)
The output is now different from our original latent growth model:
lavaan 0.6-8 ended normally after 81 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 10
Number of observations 200
Model Test User Model:
Test statistic 12.202
Degrees of freedom 10
P-value (Chi-square) 0.272
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
i =~
gpa0 1.000
gpa1 1.000
gpa2 1.000
gpa3 1.000
gpa4 1.000
s =~
gpa0 0.000
gpa1 3.000
gpa2 6.000
gpa3 9.000
gpa4 12.000
Covariances:
Estimate Std.Err z-value P(>|z|)
i ~~
s -0.000 0.001 -0.073 0.942
Intercepts:
Estimate Std.Err z-value P(>|z|)
.gpa0 0.000
.gpa1 0.000
.gpa2 0.000
.gpa3 0.000
.gpa4 0.000
i 2.602 0.018 140.832 0.000
s 0.035 0.002 16.444 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.gpa0 0.069 0.009 7.263 0.000
.gpa1 0.068 0.008 8.628 0.000
.gpa2 0.056 0.006 9.195 0.000
.gpa3 0.036 0.005 7.997 0.000
.gpa4 -0.001 0.005 -0.121 0.903
i 0.034 0.007 4.577 0.000
s 0.001 0.000 5.880 0.000
In the output above, even though $\chi^2=12.202$ and $df=10$ is the same between the two specifications, the mean of the slopes is different ($0.104$ vs. $0.035$). For the model where we specified ordinal time (loadings of $0,1,2,3,4$) the interpretation of the mean slope parameter is, for every semester (i.e., one-unit increase) in time, average GPA goes up by $0.104$ points. In contrast for the model with measured time (i.e., loadings of $0, 3, 6, 9, 12$), the interpretation becomes for every one month increase in time, average GPA would increase by $0.035$ points (note $0.035*3=.105$ which is roughly equal to the $0.104$ we obtained before). Not surprisingly, the mean of the intercept factor is the same between both parameterizations ($2.602$) since we specified baseline to be $0$ for both. If we had specified $-1$ for one of the parameterizations then the mean intercept would also differ. For more information about fixed and free parameters see Confirmatory Factor Analysis (CFA) in R with lavaan. Finally, note again the Heywood case where the residual variance of .gpa4 was estimated to be negative. In the following section we will discover a way to resolve the warning by equating the LGM to the hierarchical linear model (HLM).
Quiz
True or false. Suppose the last semester was four months long instead of three. If we continue to use ordinal time (i.e., 0,1,2,3,4), the mean of the slope factor would still be interpreted as the increase in GPA for every one semester increase in time.
Answer: False. Ordinal time assumes that the distance between orders are equivalent. If the distances are different from one time to another, then the interpretation of the mean slope would not be accurate.
True or false. Suppose the last semester was four months long instead of three. Using measured time would be more representative.
Answer: True. We would use loadings of (0, 3, 6, 9, 13) and the interpretation of the mean slope would then still be for every one month increase.
From the quiz above, we realize that if time intervals are unequal it may be better to use measured time. The only precaution is that unequal time intervals must not be truly continuous. For example, if you had time measured intermittently at $1.25, 1.26, 1.28$ seconds and organized the outcome in multivariate format, the data would contain many sparse columns (missing data) since few participants would be measured at exactly the same time. In such a case, it may be better to use ordinal time, sacrificing the interpretation of the mean slope parameter in favor of the more general one-unit increase in time (where the definition of unit may differ from participant to participant).
Equivalence of the LGM to the hierarchical linear model (HLM)
As mentioned previously, with some slight modifications LGMs can be re-specified as an equivalent hierarchical linear model (HLM). The first modification is the format of the dataset. First, we must ensure that the dataset is in long format which means that repeated observations of time span multiple rows of data for every subject. An example is:
student gpa time sex 1 2.3 0 1 1 2.1 1 1 1 3 2 1 1 3 3 1 1 3 4 1
Here the first student is a male student with time that spans five semesters, with the GPA listed for each semester. Note that time is listed ordinally, starting at $0$ and ending at $4$, such that time can be interpreted as a semester increase. The student’s gender is listed as female (sex = 1) and is time-invariant (same value repeated down the rows). In our study, the HLM consists of repeated observations at Level 1 nested within students at Level 2; where $i$ is the index for the timepoint and $j$ is the index for the student:
$$ \begin{matrix} y_{ij} = \beta_{0j} + \beta_{1j}*TIME_{ij} + r_{ij} \\ \beta_{0j} = \gamma_{00} + u_{0j} \\ \beta_{1j} = \gamma_{10} + u_{1j} \end{matrix} $$
or in combined form as
$$ \begin{matrix} y_{ij} = \gamma_{00} +\gamma_{10} *TIME_{ij} + u_{0j} + u_{1j}*TIME_{ij} + r_{ij} \end{matrix} $$
where $r_{ij} \sim N(0,\sigma^2)$ and $$\begin{pmatrix} u_{0j} \\ u_{1j} \end{pmatrix} \sim N \begin{bmatrix} \begin{pmatrix} 0 \\ 0 \end{pmatrix} , \begin{pmatrix} \tau_{00} & \\ \tau_{10} & \tau_{11} \end{pmatrix} \end{bmatrix} $$
The LGM model is equivalent to an HLM model with time nested within students with the following specifications: a) the inclusion of a fixed effect of time at Level 1 and b) the addition of a random intercept clustered by student and a random slope of time. In lmer, the syntax gpa ~ indicates that GPA is the univariate dependent variable, time is the fixed effect of time, and + (time|student) indicates random intercept and time slope. If we only wanted the random intercept term, we would use + (1|student).
m3 <- lmer(gpa ~ time + (time|student),dat=longdat) summary(m3)
The truncated output appears as:
Random effects:
Groups Name Variance Std.Dev. Corr
student (Intercept) 0.043903 0.2095
time 0.006083 0.0780 -0.15
Residual 0.047025 0.2169
Number of obs: 1000, groups: student, 200
Fixed effects:
Estimate Std. Error t value
(Intercept) 2.600500 0.018989 136.95
time 0.105350 0.007344 14.35
Correlation of Fixed Effects:
(Intr)
time -0.423
The output in lmer gives the variance of the intercept ($\hat{\tau}_{00} = 0.0451$), slope ($\hat{\tau}_{11} = 0.0451$) and the correlation of the two but not the covariance. To obtain the covariance, the easiest method is to use the function VarCorr() which takes in an lmer object and then pass the result into as.data.frame() to generate a table as shown below:
> as.data.frame(VarCorr(m3))
grp var1 var2 vcov sdcor
1 student (Intercept) <NA> 0.043903051 0.20953055
2 student time <NA> 0.006083382 0.07799604
3 student (Intercept) time -0.002395832 -0.14660086
4 Residual <NA> <NA> 0.047025026 0.21685255
All output above are either variances or covariances; the inclusion of the <NA> term in the var2 column indicates that the Level 2 parameter refers to a variance and not covariance. The first row indicates the variance of the random intercept $\hat{\tau}_{00} = 0.04$ and the second row the variance of the random slope of time $\hat{\tau}_{11} = 0.006$. These two terms have been reported previously from the lmer summary. The third row is the new row indicating the covariance of the intercept and slope $\hat{\tau}_{10}=-0.0014$. However, you will notice that this estimate (along with $\hat{\tau}_{00}$) and are not the same between the latent growth and HLM specifications. Finally in the fourth row, the <NA> term appears in both var1 and var2 columns suggesting that this is a Level 1 variance of the residuals, $\hat{\sigma}=0.047$.
The important difference between the default LGM and HLM is that the residual variances of the LGM $\theta_{\delta}$ are unconstrained across timepoints but are constrained to be the same across time in an HLM ($\sigma$) by default. In order to constrain the residual variances in an LGM, we can use the a* notation as discussed in the lavaan syntax cheatsheet section above.
m4 <- 'i =~ 1*gpa0 + 1*gpa1 + 1*gpa2 + 1*gpa3 + 1*gpa4
s =~ 0*gpa0 + 1*gpa1 + 2*gpa2 + 3*gpa3 + 4*gpa4
gpa0 ~~ a*gpa0
gpa1 ~~ a*gpa1
gpa2 ~~ a*gpa2
gpa3 ~~ a*gpa3
gpa4 ~~ a*gpa4'
fit_m4 <- growth(m4, data=widedat)
summary(fit_m4)
The truncated output is as follows
Covariances:
Estimate Std.Err z-value P(>|z|)
i ~~
s -0.002 0.002 -1.063 0.288
Intercepts:
Estimate Std.Err z-value P(>|z|)
.gpa0 0.000
.gpa1 0.000
.gpa2 0.000
.gpa3 0.000
.gpa4 0.000
i 2.600 0.019 137.290 0.000
s 0.105 0.007 14.382 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.gpa0 (a) 0.047 0.003 17.321 0.000
.gpa1 (a) 0.047 0.003 17.321 0.000
.gpa2 (a) 0.047 0.003 17.321 0.000
.gpa3 (a) 0.047 0.003 17.321 0.000
.gpa4 (a) 0.047 0.003 17.321 0.000
i 0.044 0.007 5.917 0.000
s 0.006 0.001 5.447 0.000
You will see now that the residual variances (i.e., $\hat{\theta}_{\delta}$) are constrained to be equal across all four timepoints. We can confirm that the covariance of the intercept and slope is $\hat{\phi}_{21}=-0.002$ and $\hat{\theta}_{\delta}=0.047$ from lavaan matches the output from lmer, showing (without mathematical proof) the equivalence of the latent growth and HLM models. The interpretation of the output is thus exactly the same for the LGM as it is for the HLM.
Summary of the relationship between LGM and HLM parameters
As we have seen, the latent growth model in its basic form (i.e., intercept and linear slope) is equivalent to the hierarchical linear model (HLM) with random intercept and slope on the condition that the residual variances or $\theta_{\delta}$ terms in the latent growth model are constrained to be equivalent across time. The table below shows the equivalence of the HLM parameter on the left and the corresponding latent growth parameter on the right.
- $\gamma_{00} \equiv \kappa_{1}$ intercept fixed effect
- $\gamma_{10} \equiv \kappa_{2}$ slope fixed effect
- $\tau_{00} \equiv \phi_{11}$ variance of the random intercept
- $\tau_{11} \equiv \phi_{22}$ variance of the random slope
- $\tau_{10} \equiv \phi_{21}$ covariance of the random intercept and slope
- $\sigma \equiv \theta_{\delta}$ (homogenous) residual variance
Quiz
True or false. In Raudenbush and Bryk notation, $\tau_{00}$ is the variance of the random intercept, $\tau_{11}$ is the variance of the random slope and $\tau_{10}$ is the correlation of the random intercept and slope.
Answer: False. $\tau_{10}$ is the covariance of the random intercept and slope not the correlation. By default, lmer() gives the correlation, which is why we needed to use as.data.frame(VarCorr(m3)) to obtain the covariance.
Adding a predictor to the latent growth model (LGM)
The prior section introduced the fundamental latent growth model with an intercept and linear growth factor. This model sufficiently addresses the question of whether the linear trajectory is increasing, decreasing or flat over time. In our example, we found that GPA increases by $0.105$ on average for every one semester increase in time. Other researchers may be interested in finding casual (using the word loosely) predictors of this linear trajectory. For example, we found that the trajectory of GPA increases over time, but does gender predict this trend? More specifically, are there gender differences in either the starting GPA (intercept factor) or the growth trajectory (slope factor)? To find out, we would need to include an observed predictor of the latent mean and slope terms.
Technical notes about LGMs with a predictor
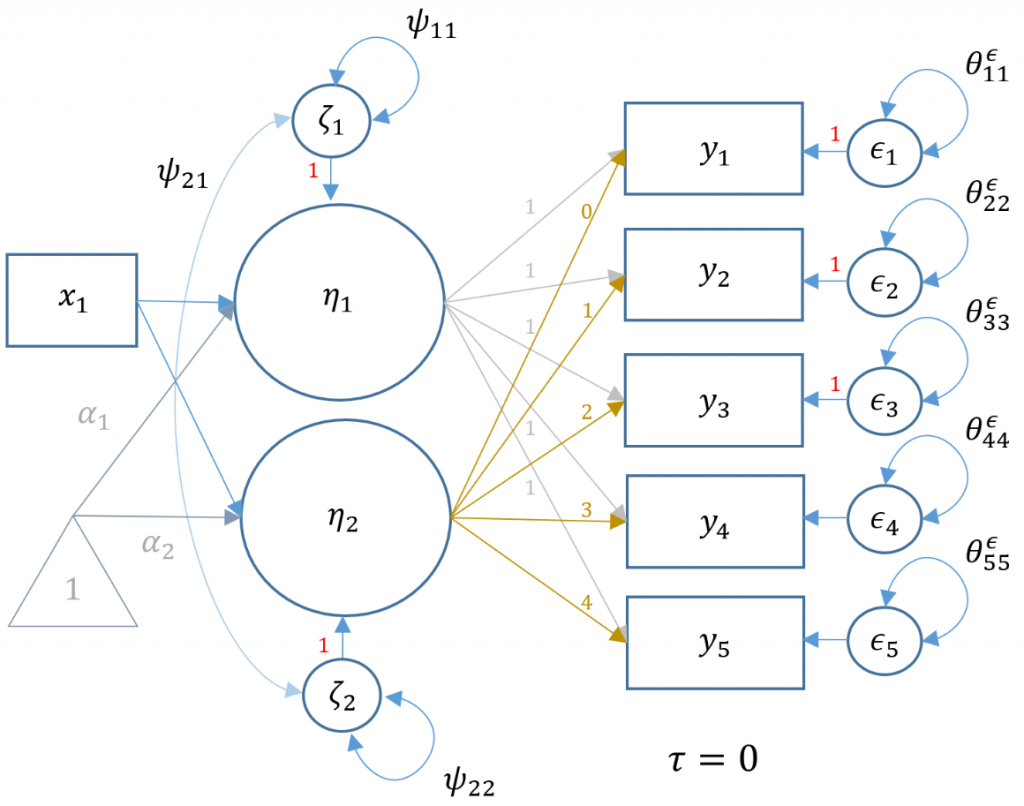
Although not necessary for full comprehension of this model, some technical understanding will aid the researcher in interpreting the output. First, since the latent factors now have a predictor, the latent intercept and slope factors become endogenous y-side variables. As such, the direction of the arrows switch from left-pointing to right-pointing. The matrix notation thus changes from $\xi, \phi,$ and $\delta$ to $\eta, \psi,$ and $\epsilon$ for the latent factor, factor variance and observed residuals respectively. Since the factor $\eta$ is now endogenous, there is a residual term $\zeta$ which was not in the exogenous model. However, the researcher can simply replace the variance of factor in the first model with the residual factor term $\psi$ in the current model. Second, in traditional LISREL notation, it is not possible to use an exogenous observed indicator (in this case gender) to predict the latent factor. The solution would be to create an artificial factor with a single item, where the loading would be constrained to $1$ and the item residual variance to $0$ (see Model 6C (Manual Specification) in Introduction to Structural Equation Modeling (SEM) in R with lavaan for more information). In modern languages like lavaan and Mplus however, the matrix formulations have been broadened to encompass paths from x-side indicators to latent factors.
Understanding the LGM with a predictor
If the reader skipped the preceding technical note, then just know that some of the parameters from the lavaan output will appear different from the previous model. The path diagram below represents the same latent growth model of GPA measured at five time points, but with gender an the exogenous predictor (i.e., $x_1$ which is a dummy variable of 1=female, 0=male).
The following syntax shows how to model the representation of the path diagram above, where gender is labeled sex. The fixed loadings of the intercept and slope factors are the same between the two models. Recall that we constrain the residual variance of GPA to be the same across timepoints to show equivalency with HLM. In order to specify gender as a predictor of the intercept use syntax i ~ sex and slope use s ~ sex to denote regression rather than measurement paths.
m5 <- 'i =~ 1*gpa0 + 1*gpa1 + 1*gpa2 + 1*gpa3 + 1*gpa4
s =~ 0*gpa0 + 1*gpa1 + 2*gpa2 + 3*gpa3 + 4*gpa4
i ~ sex
s ~ sex
gpa0 ~~ a*gpa0
gpa1 ~~ a*gpa1
gpa2 ~~ a*gpa2
gpa3 ~~ a*gpa3
gpa4 ~~ a*gpa4'
fit_m5 <- growth(m5, data=widedat)
summary(fit_m5)
The lavaan output is as follows:
lavaan 0.6-8 ended normally after 55 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 12
Number of equality constraints 4
Number of observations 200
Model Test User Model:
Test statistic 107.504
Degrees of freedom 17
P-value (Chi-square) 0.000
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|)
i =~
gpa0 1.000
gpa1 1.000
gpa2 1.000
gpa3 1.000
gpa4 1.000
s =~
gpa0 0.000
gpa1 1.000
gpa2 2.000
gpa3 3.000
gpa4 4.000
Regressions:
Estimate Std.Err z-value P(>|z|)
i ~
sex 0.068 0.038 1.805 0.071
s ~
sex 0.035 0.014 2.396 0.017
Covariances:
Estimate Std.Err z-value P(>|z|)
.i ~~
.s -0.003 0.002 -1.343 0.179
Intercepts:
Estimate Std.Err z-value P(>|z|)
.gpa0 0.000
.gpa1 0.000
.gpa2 0.000
.gpa3 0.000
.gpa4 0.000
.i 2.565 0.027 94.080 0.000
.s 0.087 0.010 8.317 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.gpa0 (a) 0.047 0.003 17.321 0.000
.gpa1 (a) 0.047 0.003 17.321 0.000
.gpa2 (a) 0.047 0.003 17.321 0.000
.gpa3 (a) 0.047 0.003 17.321 0.000
.gpa4 (a) 0.047 0.003 17.321 0.000
.i 0.042 0.007 5.850 0.000
.s 0.006 0.001 5.315 0.000
From the output we can see that gender does not significantly predict the intercept ($p = 0.071$), but gender predicts the linear slope ($p < 0.05$). This implies that female and male students do not differ in their starting GPA’s in the first semester of school (females have an estimated $0.068$ higher GPA compared to males but the standard error does not warrant statistical significance). However, gender predicts the slope so that female students have a linear growth trajectory that is $0.035$ GPA units higher than male students across these five semesters.
Exercise 1 (Challenge)
Recall that LGMs are a special type of CFA model. Try to match m5 with cfa() instead of growth(). What is wrong with this output? Look at the path diagram to see what manual specification is needed.
m6 <- 'i =~ 1*gpa0 + 1*gpa1 + 1*gpa2 + 1*gpa3 + 1*gpa4
s =~ 0*gpa0 + 1*gpa1 + 2*gpa2 + 3*gpa3 + 4*gpa4
i ~ sex
s ~ sex
#constrain the residual variances
gpa0 ~~ a*gpa0
gpa1 ~~ a*gpa1
gpa2 ~~ a*gpa2
gpa3 ~~ a*gpa3
gpa4 ~~ a*gpa4'
fit_m6 <- cfa(m6, data=widedat,meanstructure=TRUE)
summary(fit_m6)
Notice in the output below that the observed means for GPA are all freely estimated and which makes the latent means zero.
Intercepts:
Estimate Std.Err z-value P(>|z|)
.gpa0 2.558 0.029 88.402 0.000
.gpa1 2.662 0.028 96.681 0.000
.gpa2 2.738 0.029 93.840 0.000
.gpa3 2.828 0.033 84.596 0.000
.gpa4 2.911 0.039 73.785 0.000
.i 0.000
.s 0.000
Instead, we want to identify the latent means by constraining the observed intercepts to zero using gpa0 ~ 0 (other GPAs not shown). Additionally, we use i ~ 1 and s ~ 1 to freely estimate the mean of the latent intercept and slope. Check that the syntax below recreates the output from m5.
m7 <- 'i =~ 1*gpa0 + 1*gpa1 + 1*gpa2 + 1*gpa3 + 1*gpa4
s =~ 0*gpa0 + 1*gpa1 + 2*gpa2 + 3*gpa3 + 4*gpa4
#observed intercepts constrained to 0
gpa0 ~ 0
gpa1 ~ 0
gpa2 ~ 0
gpa3 ~ 0
gpa4 ~ 0
#constrain the residual variances
gpa0 ~~ a*gpa0
gpa1 ~~ a*gpa1
gpa2 ~~ a*gpa2
gpa3 ~~ a*gpa3
gpa4 ~~ a*gpa4
#estimate intercept and slope means, add gender as a predictor
i ~ 1 + sex
s ~ 1 + sex'
fit_m7 <- cfa(m7, data=widedat, meanstructure=TRUE)
summary(fit_m7)
Equivalence of the LGM to an HLM with a time predictor
Adding a predictor of the intercept and slope can be specified equivalently in HLM. Again we are working with repeated observations $i$ nested within students $j$:
$$ \begin{matrix} y_{ij} = \beta_{0j} + \beta_{1j}*TIME_{ij} + r_{ij} \\ \beta_{0j} = \gamma_{00} + \gamma_{01}*GENDER_{j} + u_{0j} \\ \beta_{1j} = \gamma_{10} +\gamma_{11}* GENDER_{j} + u_{1j} \end{matrix} $$
Here in the multilevel formulation, GENDER is a predictor of the intercept $\beta_{0j}$ as well as the slope $beta_{1j}$. However, in combined form which is an algebraic manipulation of the multilevel formulation above, the prediction of GENDER on the intercept now becomes the simple effect of gender and the prediction of GENDER on the slope now because the TIME*GENDER interaction:
$$ \begin{matrix} y_{ij} = \gamma_{00} + \gamma_{01}*GENDER_{j} + \gamma_{10} *TIME_{ij} + \gamma_{11}*GENDER_{j}*TIME_{ij} + u_{0j} + u_{1j}*TIME_{ij} + r_{ij} \end{matrix} $$
where $r_{ij} \sim N(0,\sigma^2)$ and
$$\begin{pmatrix} u_{0j} \\ u_{1j} \end{pmatrix} \sim N \begin{bmatrix} \begin{pmatrix} 0 \\ 0 \end{pmatrix} , \begin{pmatrix} \tau_{00} & \\ \tau_{10} & \tau_{11} \end{pmatrix} \end{bmatrix} $$
The formulations above suggest that our LGM with a single predictor of the intercept and slope is equivalent to an HLM of repeated observations nested within students given the following specifications: a) inclusion of the fixed effects of time, gender and the interaction of time and gender, and b) specification of the random intercept clustered by student with a random slope of time. In lmer, the syntax gpa ~ indicates that GPA is the dependent variable, time + sex are the simple fixed effects, and time:sex is the interaction of time and gender. The addition of + (time|student) indicates that we want the random intercept to be clustered by student, with a random slope for time. If we wanted only random intercept by student we would use + (1|student) with the 1 indicating the intercept.
m8 <- lmer(gpa ~ time + sex + time:sex + (time|student),dat=longdat) summary(m8)
The output is as follows:
Random effects:
Groups Name Variance Std.Dev. Corr
student (Intercept) 0.043105 0.20762
time 0.005835 0.07639 -0.19
Residual 0.047025 0.21685
Number of obs: 1000, groups: student, 200
Fixed effects:
Estimate Std. Error t value
(Intercept) 2.56484 0.02740 93.609
time 0.08716 0.01053 8.276
sex 0.06792 0.03782 1.796
time:sex 0.03465 0.01454 2.384
Correlation of Fixed Effects:
(Intr) time sex
time -0.454
sex -0.725 0.329
time:sex 0.329 -0.725 -0.454
To obtain the variances and covariances:
> as.data.frame(VarCorr(m8))
grp var1 var2 vcov sdcor
1 student (Intercept) <NA> 0.043105253 0.20761805
2 student time <NA> 0.005835224 0.07638864
3 student (Intercept) time -0.003048018 -0.19218685
4 Residual <NA> <NA> 0.047025167 0.21685287
We can see from the output that the variance terms match that of the LGM. Most notably, we note that the covariance of the intercept and slope is the same as the LGM, where $\hat{\tau}_{10} = \hat{\phi}_{21} = -.003$. Sample output is shown below.
Covariances:
Estimate Std.Err z-value P(>|z|)
.i ~~
.s -0.003 0.002 -1.343 0.179
Refer the to section Summary of the relationship between LGM and HLM parameters and verify that indeed all the parameters estimated in the HLM are equivalent to the LGM.
Quiz
True or false. A predictor with a path to the intercept and slope in an LGM is equivalent to the simple effect of that predictor, the simple effect of time, and the interaction of the predictor with time in the combined form of the HLM.
Answer: True.
True or false. One difference between the LGMs and the HLMs is that in the former, the residual variances are (by default) unconstrained but in the latter they are homogeneous (constrained to be equal).
Answer: True.
True or false. The LGM requires that the data be long whereas the HLM requires that the data be wide.
Answer: False. LGM requires wide or multivariate data and HLM requires long or univariate data.
Measurement Invariance
We now proceed into an entirely different topic which involves how to run CFAs for subgroups of the participants. Suppose we were no longer interested in the gender differences in the trajectory of growth, but rather we want to see whether achievement measured as a construct is measured similarly between genders. The first step in addressing this research question is to stratify your CFA in what is known as a multigroup CFA. Much like adding gender as a predictor in our HLM model above, multigroup CFA is akin to a regression with a categorical variable (see Decomposing, Probing, and Plotting Interactions in R). However, unlike linear regression models which assume outcomes are measured perfectly, CFA models are based on the premise that there is measurement error, which must be modeled. When speaking of multiple groups, measurement error may manifest itself differently. The logic is then, if the measurement itself differs between groups, then it is not possible to compare latent constructs. In our example, suppose student achievement is measured differently for males and females, comparing achievement between genders can lead to to incorrect conclusions. This situation is common in standardized testing, whereby certain items may be more biased towards boys’ experiences (e.g., items related to team sports or technology) and not a true measure of underlying student achievement. In the literature, this is known as differential item functioning, which is typically not desirable as it leads to implications of testing bias. Measurement invariance is thus desired and must be established as the first step in the comparison of constructs across groups. However, in terms of model fit, measurement invariance models as a nested model of the measurement variant or configural model must necessarily be worse. To achieve measurement invariance the model fit should be no worse than the configural model. As such, we want to fail to reject the null hypothesis that the models are different.
Measurement invariance is a very important requisite in multigroup CFA/SEM. Establishment of measurement invariance verifies the underlying latent construct (e.g., student achievement or depression) is measured consistently across groups. However, the establishment of measurement (weak) invariance is not sufficient. Arguably scalar (strong) invariance is more desirable as it allows for comparisons in the latent construct across groups. Without the establishment of scalar invariance, even if the construct is measured similarly across groups, the researcher cannot make comparative claims about the latent construct. Residual invariance makes an even stronger claim than scalar invariance, in that any variance not attributed to the construct is also equivalent across groups. This claim is often times unachievable in practice, and may not make theoretical sense if the residual variance is thought to stem from unsystematic rather than systematic sources. Finally, all these models are simply claims about the construct, and its veracity must be assessed through model fit comparisons (a.k.a chi-square difference testing). For example, even if the researcher were to fit a scalar invariant model which claims that males perform better than females in terms of academic achievement and yet model fit comparisons suggest departure from the metric invariance model, the claim would actually be inconclusive. More details are discussed in the section on Model fit comparisons of invariance models.
Single group CFA
The High School and Beyond dataset is a survey of academic performance of representative US high schools. The hsbdemo is a modified version of this survey reduced down to only 200 students for the purposes of this seminar (download hsbdemo.csv). Students are assessed in four content areas, reading, writing, mathematics and science. Our goal is to create a single construct (i.e., factor) of academic performance based on these four item types. The ultimate goal of this particular study is to see whether there are gender differences in academic performance among this particular group of high school students.
To construct this academic performance factor, we need to fit a CFA model. As we already know from the seminars Confirmatory Factor Analysis (CFA) in R with lavaan and Introduction to Structural Equation Modeling (SEM) in R with lavaan, fitting a this model involves specifying a latent exogenous measurement model with four x-side indicators ($x_1, x_2, x_3, x_4$) corresponding to reading, writing, mathematics and science, measured by the factor $\xi_1$. The un-identified measurement model for this exogenous factor with four indicators is:
$$ \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{pmatrix} = \begin{pmatrix} \tau_{1} \\ \tau_{2} \\ \tau_{3} \\ \tau_{4} \end{pmatrix} + \begin{pmatrix} \lambda_{11} \\ \lambda_{21} \\ \lambda_{31} \\ \lambda_{41} \end{pmatrix} \xi_{1} + \begin{pmatrix} \delta_{1} \\ \delta_{2} \\ \delta_{3} \\ \delta_{4} \end{pmatrix} $$
This one-factor CFA will be used in all subsequent measurement models.
Multigroup CFA
Suppose we wanted to assess males and females separately in terms of academic achievement. The multigroup CFA simply means a CFA model stratified by two or more groups, in this case gender. First let’s split the dataset into two strata, one for males and the other for females. Using the function subset, we can subset our original data and store them into their corresponding objects, femaledat and maledat.
femaledat<- subset(hsbdemo,female=="female") maledat<- subset(hsbdemo,female=="male") > dim(femaledat) [1] 109 13 > dim(maledat) [1] 91 13
From an inspection of the dimension of the data (first element is the number of rows in the dataset and the second is the number of columns), we see that there are 109 females and 91 males in our sample each with 13 variables. We then run a separate CFA for each of the two datasets separately, making sure to request meanstructure = TRUE so that we can estimate the intercepts for each indicator. Some elements of the output have been omitted for brevity. [FIX] The first thing we have to do is specify the CFA model.
#separate cfa models
onefac <- 'f1 =~ read + write + math + science'
#equivalent meanstructure
onefac_b <- 'f1 =~ read + write + math + science
read ~ 1
write ~ 1
math ~ 1
science ~ 1'
We can then fit separate CFA models for males and females. First, split the hsbdemo dataset into two parts.
femaledat<- subset(hsbdemo,female=="female") maledat<- subset(hsbdemo,female=="male")
Using the function dim() we can see the number of rows of students and the number of column of variables.
> dim(femaledat) [1] 109 13 > dim(maledat) [1] 91 13
We see that there are 109 females and 91 males in our dataset which totals to 200 students, each with 13 variables. Now for each gender, we fit a separate CFA model as if we had two datasets, femaledat and maledat.
fitfemale <- cfa(onefac, data = femaledat, meanstructure = TRUE)
> summary(fitfemale, standardized=TRUE)
lavaan 0.6-8 ended normally after 46 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 12
Number of observations 109
Model Test User Model:
Test statistic 1.903
Degrees of freedom 2
P-value (Chi-square) 0.386
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~
read 1.000 8.006 0.800
write 0.801 0.091 8.769 0.000 6.414 0.792
math 0.985 0.102 9.621 0.000 7.889 0.866
science 0.863 0.102 8.453 0.000 6.912 0.768
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 51.734 0.959 53.949 0.000 51.734 5.167
.write 54.991 0.775 70.911 0.000 54.991 6.792
.math 52.394 0.872 60.052 0.000 52.394 5.752
.science 50.697 0.862 58.830 0.000 50.697 5.635
f1 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 36.133 6.426 5.623 0.000 36.133 0.360
.write 24.410 4.271 5.716 0.000 24.410 0.372
.math 20.736 4.693 4.419 0.000 20.736 0.250
.science 33.165 5.555 5.971 0.000 33.165 0.410
f1 64.099 13.331 4.808 0.000 1.000 1.000
fitmale <- cfa(onefac, data = maledat, meanstructure = TRUE)
> summary(fitmale, standardized=TRUE)
lavaan 0.6-8 ended normally after 44 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 12
Number of observations 91
Model Test User Model:
Test statistic 0.719
Degrees of freedom 2
P-value (Chi-square) 0.698
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~
read 1.000 8.531 0.816
write 0.954 0.119 7.983 0.000 8.137 0.794
math 0.863 0.113 7.663 0.000 7.361 0.766
science 0.999 0.124 8.031 0.000 8.521 0.798
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 52.824 1.095 48.227 0.000 52.824 5.056
.write 50.121 1.074 46.653 0.000 50.121 4.891
.math 52.945 1.008 52.548 0.000 52.945 5.508
.science 53.231 1.119 47.577 0.000 53.231 4.987
f1 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 36.404 7.769 4.686 0.000 36.404 0.333
.write 38.825 7.775 4.993 0.000 38.825 0.370
.math 38.197 7.210 5.298 0.000 38.197 0.413
.science 41.300 8.365 4.937 0.000 41.300 0.363
f1 72.774 16.251 4.478 0.000 1.000 1.000
Note that the model parameters are the same because we did not change the factor structure, but the loadings, intercepts and variances are different across groups. At this point the researcher can make a qualitative observation of whether the measurement model differs between males and females. For example, the loadings for the factor appear to range between $.80$ to $.99$ given the marker method fixed at the first loading (reading). It appears that the measurement of the achievement construct is similar between male and female students. However to make statistical claims about measurement invariance, we must first understand its four fundamental models, 1) configural, 2) metric, 3) scalar and 4) residual invariance.
Configural invariance
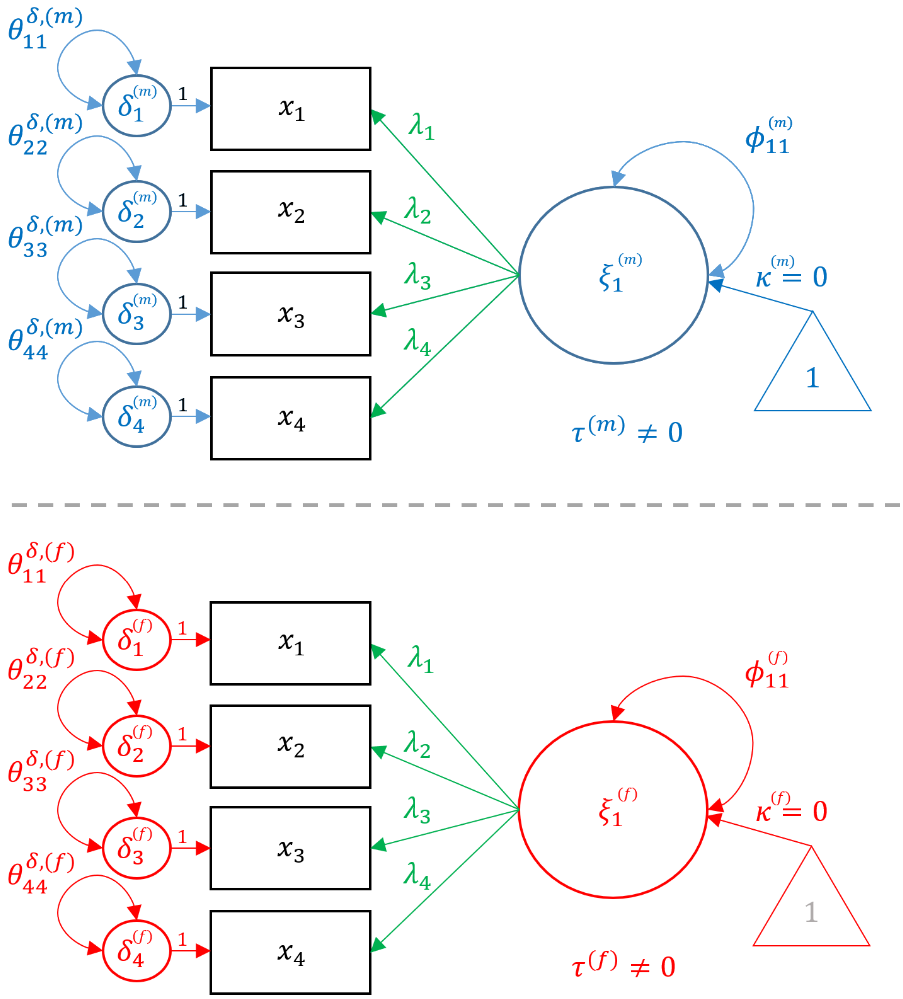
Now that we have fit two separate CFA’s for males and females, we should understand the configural invariant model, which is defined as a multigroup CFA model with the same number of items loaded onto the same number of factors, but no constraints across groups other than for identification (i.e., marker method or variance standardization method). Among the four fundamental models, the configural invariant model is the best model achievable. This is because allowing the intercepts, loadings and variances to differ across groups is the model that fits the existing data most closely. Any other nested model (i.e., metric, strong, residual invariance) will be only as good as the configural invariance model. The reason for the name configural invariance is that the configuration of the factor structure remains the same (i.e., four x-side indicators loaded onto one factor)
The configural model looks exactly like the single group CFA model except parameters are indexed by the grouping variable (i.e., gender). Notice the indicators ($x_i$) stay the same across genders because the data comes from the same source but just that the parameters are stratified. Although not shown for generality, the constraints of $1$ for the first factor loading (marker method) or $1$ for the variance (variance standardization) must be applied and hold independently of measurement invariance (see Confirmatory Factor Analysis (CFA) in R with lavaan). These factor identification rules apply to the current model (Configural) and all subsequently constrained models (Metric, Scalar and Residual).
For males the CFA model is described in equation form as:
$$ \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{pmatrix} = \begin{pmatrix} \tau^{(m)}_{1} \\ \tau^{(m)}_{2} \\ \tau^{(m)}_{3} \\ \tau^{(m)}_{4} \end{pmatrix} + \begin{pmatrix} \lambda^{(m)}_{11} \\ \lambda^{(m)}_{21} \\ \lambda^{(m)}_{31} \\ \lambda^{(m)}_{41} \end{pmatrix} \xi_{1} + \begin{pmatrix} \delta^{(m)}_{1} \\ \delta^{(m)}_{2} \\ \delta^{(m)}_{3} \\ \delta^{(m)}_{4} \end{pmatrix} $$
For females,
$$ \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{4} \end{pmatrix} = \begin{pmatrix} \tau^{(f)}_{1} \\ \tau^{(f)}_{2} \\ \tau^{(f)}_{3} \\ \tau^{(f)}_{4} \end{pmatrix} + \begin{pmatrix} \lambda^{(f)}_{11} \\ \lambda^{(f)}_{21} \\ \lambda^{(f)}_{31} \\ \lambda^{(f)}_{41} \end{pmatrix} \xi_{1} + \begin{pmatrix} \delta^{(f)}_{1} \\ \delta^{(f)}_{2} \\ \delta^{(f)}_{3} \\ \delta^{(f)}_{4} \end{pmatrix} $$
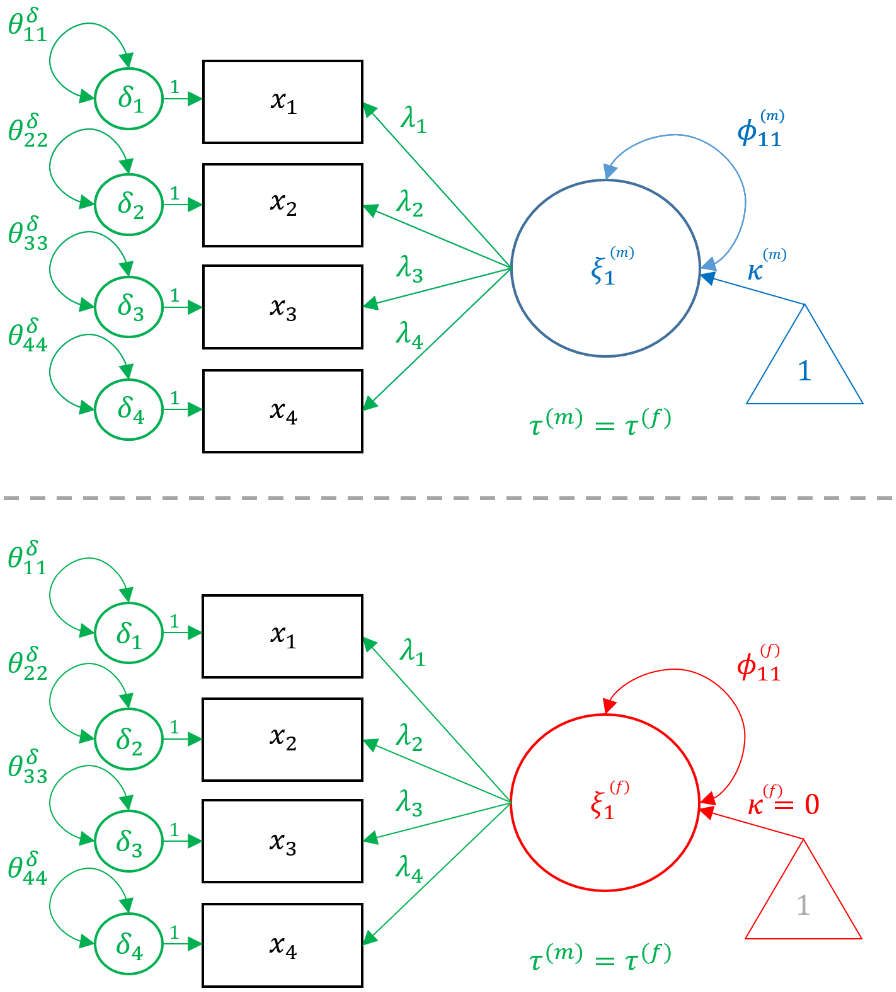
Notice that the loadings $\lambda$’s, item intercepts $\tau$’s, and residual variances $\delta$’s vary across genders but the indices (e.g., $\lambda_{21}$) remain the same. This is because the configural invariance implies that the configuration of the factor model remains the same across genders, and is essentially the same as running two identical CFA models. In the following sections, we will show how constraining each of these three parameters to be the same across groups corresponds to a specific type of invariant model. In the path diagram below, the items are in black because it is shared across groups and parameters unique to males are in blue, whereas parameters unique to females are in red.
 In order to fit the Configural model in
In order to fit the Configural model in lavaan, pass in the same onefac model as defined for the single group CFA and specify group = "female" which request the multigroup configural invariance model. Note that the dataset here is the entire dataset not just a subset of males or females, and we continue to request meanstructure = TRUE to estimate the intercepts ($\tau$’s).
fit.Configural <- cfa(onefac, data = hsbdemo, group = "female", meanstructure = TRUE) summary(fit.Configural, standardized=TRUE)
The output is presented below:
lavaan 0.6-8 ended normally after 81 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 24
Number of observations per group:
female 109
male 91
Model Test User Model:
Test statistic 2.622
Degrees of freedom 4
P-value (Chi-square) 0.623
Test statistic for each group:
female 1.903
male 0.719
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Group 1 [female]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~
read 1.000 8.006 0.800
write 0.801 0.091 8.769 0.000 6.414 0.792
math 0.985 0.102 9.621 0.000 7.889 0.866
science 0.863 0.102 8.453 0.000 6.912 0.768
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 51.734 0.959 53.949 0.000 51.734 5.167
.write 54.991 0.775 70.911 0.000 54.991 6.792
.math 52.394 0.872 60.052 0.000 52.394 5.752
.science 50.697 0.862 58.830 0.000 50.697 5.635
f1 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 36.133 6.426 5.623 0.000 36.133 0.360
.write 24.410 4.271 5.716 0.000 24.410 0.372
.math 20.736 4.693 4.419 0.000 20.736 0.250
.science 33.165 5.555 5.971 0.000 33.165 0.410
f1 64.099 13.331 4.808 0.000 1.000 1.000
Group 2 [male]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~
read 1.000 8.531 0.816
write 0.954 0.119 7.983 0.000 8.137 0.794
math 0.863 0.113 7.663 0.000 7.361 0.766
science 0.999 0.124 8.031 0.000 8.521 0.798
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 52.824 1.095 48.227 0.000 52.824 5.056
.write 50.121 1.074 46.653 0.000 50.121 4.891
.math 52.945 1.008 52.548 0.000 52.945 5.508
.science 53.231 1.119 47.577 0.000 53.231 4.987
f1 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 36.404 7.769 4.686 0.000 36.404 0.333
.write 38.825 7.775 4.993 0.000 38.825 0.370
.math 38.197 7.210 5.298 0.000 38.197 0.413
.science 41.300 8.365 4.937 0.000 41.300 0.363
f1 72.774 16.251 4.478 0.000 1.000 1.000
Notice that we have the exactly same estimates for the loadings, intercepts and variances as running the CFA’s separately for males and females. Additionally, the chi-square and degrees of freedom is exactly the sum of the two chi-squares ($1.903+0.719=2.622$) with $2+2=4$ degrees of freedom.
Quiz
True or false. Any two group model where the intercepts, loadings and variances are set to be free across groups can be called a configural invariance model.
Answer: False. If the factor structure is different across groups, configural variance would never be achieved.
True or false. Configural invariance can never be achieved in a two group model if one group has three items and the second group has four items.
Answer: True. The two groups must have exactly the same number of items loaded onto the same number of factors for configural variance.
Metric (Weak) invariance
Although configural invariance is the best model in terms of model fit, metric invariance is the more desirable model. The premise is that for a true comparison of a construct such as student achievement, the construct must be measured the same way for all groups. For example, it would not be desirable if the math and science items loaded more highly for male students and reading and writing items loaded more highly for female students. If this were the case, then student achievement would be defined more as STEM achievement for male students and verbal achievement for female students rather than an overall measure of student achievement. As such, all items should load similarly for both males and females so that educational evaluators can more confidently compare the performance of males with females. If certain items load more highly for a particular group, this is known as differential item functioning (DIF) which is undesirable in assessment. The desired property as that all items load equally across groups, a property known as metric invariance.
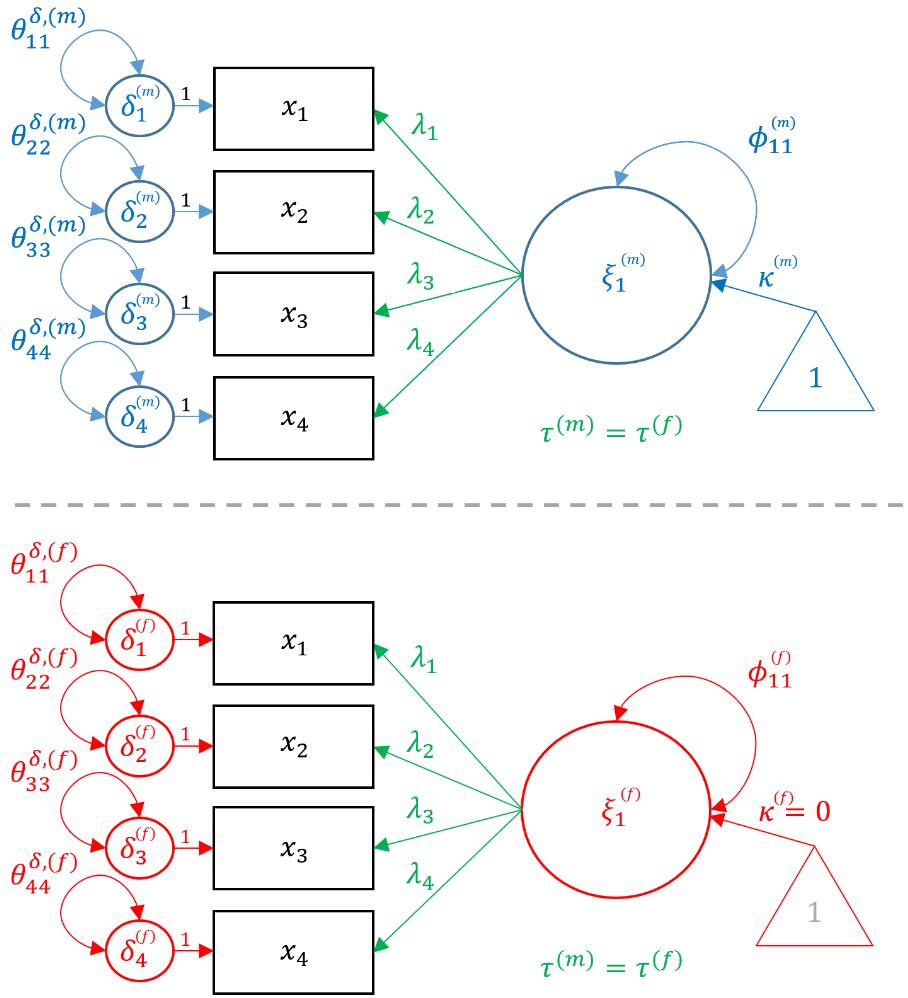
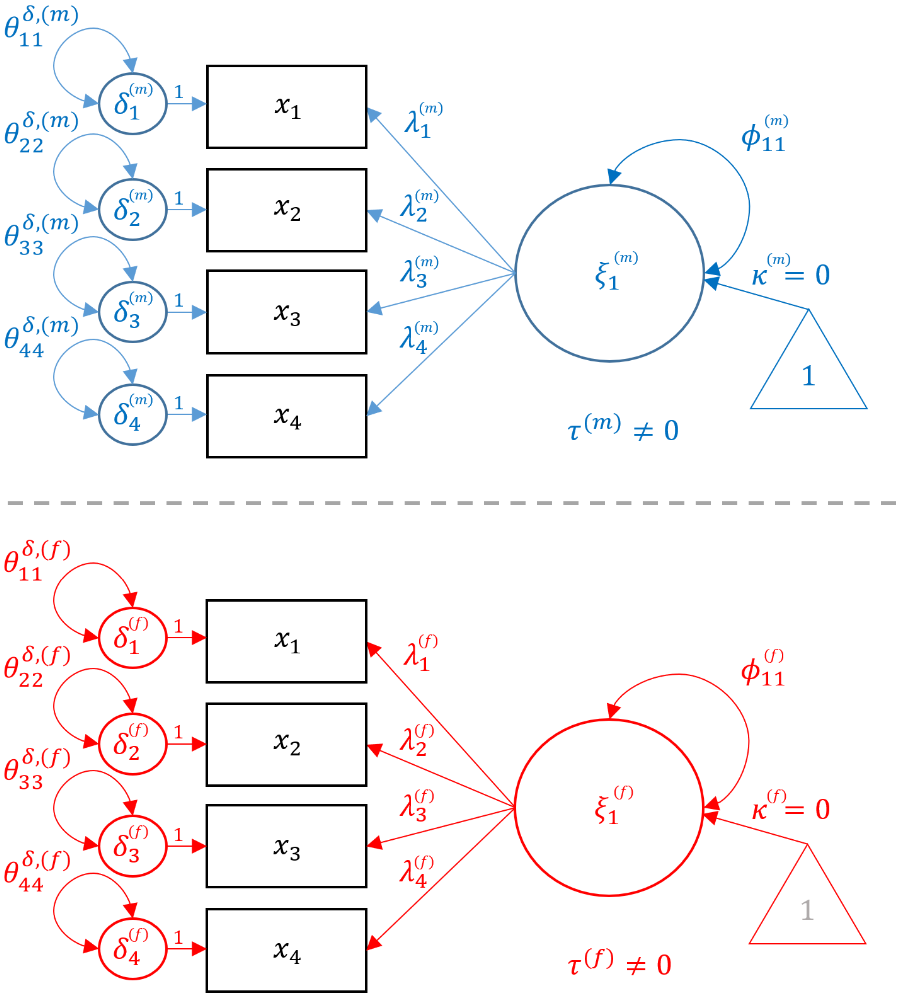
In order to fit the Metric model, first start with Configural Model, but add the constraint that $$ \lambda^{(m)}_{ij} = \lambda^{(f)}_{ij}$$ for all $i,j$. The path diagram below represents the Metric model, notice that common parameters (loadings) are in green, parameters unique to males are in blue and females in red.
In order to fit the Metric model in lavaan, recycle the same syntax as for the Configural model and add group.equal = c("loadings"). As the syntax states, this allows for the loadings $\lambda$’s to be the same across genders.
fit.Metric <- cfa(onefac, data = hsbdemo, group = "female",
group.equal = c("loadings"), meanstructure = TRUE)
summary(fit.Metric, standardized=TRUE)
The output is presented below:
lavaan 0.6-8 ended normally after 74 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 24
Number of equality constraints 3
Number of observations per group:
female 109
male 91
Model Test User Model:
Test statistic 6.801
Degrees of freedom 7
P-value (Chi-square) 0.450
Test statistic for each group:
female 3.692
male 3.109
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Group 1 [female]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~
read 1.000 7.844 0.790
write (.p2.) 0.866 0.074 11.744 0.000 6.789 0.816
math (.p3.) 0.939 0.077 12.214 0.000 7.365 0.836
science (.p4.) 0.928 0.080 11.590 0.000 7.277 0.790
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 51.734 0.951 54.410 0.000 51.734 5.212
.write 54.991 0.797 69.011 0.000 54.991 6.610
.math 52.394 0.843 62.128 0.000 52.394 5.951
.science 50.697 0.882 57.472 0.000 50.697 5.505
f1 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 37.013 6.379 5.802 0.000 37.013 0.376
.write 23.119 4.238 5.455 0.000 23.119 0.334
.math 23.282 4.536 5.133 0.000 23.282 0.300
.science 31.858 5.499 5.794 0.000 31.858 0.376
f1 61.530 11.526 5.338 0.000 1.000 1.000
Group 2 [male]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~
read 1.000 8.664 0.822
write (.p2.) 0.866 0.074 11.744 0.000 7.498 0.760
math (.p3.) 0.939 0.077 12.214 0.000 8.134 0.803
science (.p4.) 0.928 0.080 11.590 0.000 8.037 0.775
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 52.824 1.105 47.796 0.000 52.824 5.010
.write 50.121 1.034 48.484 0.000 50.121 5.082
.math 52.945 1.062 49.862 0.000 52.945 5.227
.science 53.231 1.088 48.942 0.000 53.231 5.130
f1 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 36.095 7.641 4.724 0.000 36.095 0.325
.write 41.025 7.538 5.442 0.000 41.025 0.422
.math 36.439 7.293 4.996 0.000 36.439 0.355
.science 43.048 8.114 5.305 0.000 43.048 0.400
f1 75.057 14.697 5.107 0.000 1.000 1.000
The first output to note is the addition of the labels (.p2.), (.p3.) and (.p4.) corresponding to the four loadings. This verifies that lavaan has indeed labeled the parameters (p for parameter), and equated them between genders to be $0.866$, $0.939$ and $0.928$ respectively. Before proceeding with the next model, we must keep two concepts in mind. 1) just because we constrained the loadings to be equal does not necessarily make it statistically justifiable as we must test this assumption as we will discuss under Model fit comparisons of invariance models. 2) Equating the loadings across genders pertains only to unstandardized loadings under the Estimate column. Notice that Std.all shows that the standardized loadings for writing are $0.816$ for females and $0.760$ for females even though their unstandardized loadings are the same. This is because Std.all standardizes also by the standard deviation of the x-side indicators, which may differ slightly between males and females. For more information, refer to Lesa Hoffman’s slides on Confirmatory Factor Models.
Quiz
True or false. If the chi-square of the configural invariant model is 2.62, then the chi-square of the metric invariance model must be at least 2.62 (it cannot be smaller).
Answer: True. The closest the metric invariant model can get is as good as the configural invariant model. A larger chi-square is poorer fitting so it must be at least 2.62.
Variance standardization in metric invariance
By default, lavaan uses marker method to establish model identification in multigroup CFA/SEM models, where the first loading of each item is fixed to one. Model identification is independent of the constraints placed on the loadings for metric invariance. Theoretically, this should imply that variance standardization, (another method of model identification) should provide the same fit in terms of chi-square and degrees of freedom when compared to marker method. As we will demonstrate in the following exercise, special care must be take to equate the two methods of model identification in metric invariance.
Exercise 2A
Use variance standardization method to identify the metric invariance model by un-constraining the first loading to 1 and setting the variance of the factor in both groups to 1 . Use the same one factor, 4-item configuration as before. Note the degrees of freedom and compare it to the Metric model where we used marker method. If it’s not the same, can you conjecture why this is happening?
Answer:
As we have seen in the seminar Confirmatory Factor Analysis (CFA) in R with lavaan, since lavaan uses marker method by default, we must first unconstrain the first loading. The reason we can use NA*read instead of c(NA,NA)*read is because lavaan will recycle the same syntax for the other groups if only one group is specified.
#one factor model (WRONG) variance std method
onefac_varstd <- 'f1 =~ NA*read + write + math + science
f1 ~~ c(1,1)*f1'
fit.MetricWRONG <- cfa(onefac_varstd2 , data = hsbdemo, group = "female", meanstructure = TRUE)
summary(fit.MetricWRONG)
In the following abbreviated output you will see that compared to the original (marker method version) of the Metric model, the $\chi^2_{\mbox{original}}=6.801$ with $df_{\mbox{original}}=7$ whereas for the incorrect model it is $\chi^2_{\mbox{wrong}}=7.542$ with $df_{\mbox{wrong}}=8$, where we obtained an extra degree of freedom.
Model Test User Model (ORIGINAL):
Test statistic 6.801
Degrees of freedom 7
P-value (Chi-square) 0.450
Test statistic for each group:
female 3.692
male 3.109
Model Test User Model (WRONG):
Test statistic 7.542
Degrees of freedom 8
P-value (Chi-square) 0.479
Test statistic for each group:
female 3.902
male 3.640
The extra degree of freedom in the “wrong” model stems from the fact that we fixed factor variance to one for both males and females, when we should be fixing the variance to one for females and allow the variance to be free (or unconstrained) for males; see Lesa Hoffman’s slides on Measurement Invariance for more information. In the modified (correct) version of the variance standardization, we achieve this using the syntax f1 ~~ c(1,NA)*f1; the full lavaan syntax is shown below.
#one factor, variance std method (CORRECT)
onefac_varstd <- 'f1 =~ NA*read + write + math + science
f1 ~~ c(1,NA)*f1'
# metric invariance (CORRECT)
fit.MetricCORRECT <- cfa(onefac_varstd , data = hsbdemo, group = "female",
group.equal=c("loadings"),meanstructure = TRUE)
summary(fit.MetricCORRECT)
In the truncated output below, you can see that the $\chi^2_{\mbox{correct}}=6.801$ has $df_{\mbox{correct}}=7$ which matches that of the original. Notice that the factor variance for females is fixed at one but is estimated at $1.22$ for males.
Model Test User Model:
Test statistic 6.801
Degrees of freedom 7
P-value (Chi-square) 0.450
Test statistic for each group:
female 3.692
male 3.109
Group 1 [female]:
Variances:
Estimate Std.Err z-value P(>|z|)
f1 1.000
Group 2 [male]:
Variances:
Estimate Std.Err z-value P(>|z|)
f1 1.220 0.280 4.350 0.000
Exercise 2B (Challenging)
Instead of using group.equal = c("loadings"), manually specify the Metric model from Exercise 2A using constraints.
Hint: lavaan allows for multiple modifiers. For example, if you want to free one of the loadings and label it ‘a’, you can do the following: NA*x1 + a*x1.
Answer:
The hint tells us that we can specify multiple modifiers in lavaan. First, we unconstrain the first loading in each group using c(NA,NA)*read. Second, we fix the variance of the factor for females to one, and unconstrain the factor variance for males using f1 ~~ c(1,NA)*f1. Finally, since we want to constrain the loadings to be the same across groups for all items, we add the second modifier to the reading item using c(a,a)*read and single modifiers (e.g., c(b,b)*write) to the remaining items.
onefac_varstd2 <- 'f1 =~ c(NA,NA)*read + c(a,a)*read + c(b,b)*write + c(c,c)*math + c(d,d)*science
f1 ~~ c(1,NA)*f1'
Now proceed with fitting the Metric model as before but taking out group.equal = c("loadings").
fit.MetricVS <- cfa(onefac_varstd2 , data = hsbdemo, group = "female", meanstructure = TRUE) summary(fit.MetricVS)
Check that the manual metric invariance method gives the same chi-square value and degrees of freedom as before.
From these two exercises, we have learned that variance identification requires an additional (unexpected) free parameter, but once the correct identification is established, changing the model identification from marker method to variance standardization method does not change the fit of the Metric model.
Scalar (Strong) invariance
The establishment of metric invariance allows us to more confidently state that the construct of academic achievement is measured equivalently across genders but does not allow us. However, only scalar invariance allows us to compare achievement between genders. For scalar invariance in a CFA, a reference group must be chosen such that its factor mean is set to zero and all other groups are either lower or higher relative to that group. In our analysis, we choose females to be the reference group which constrains their achievement mean to be zero. To allow us to fix the latent mean of one group, the observed intercepts ($\tau$’s) of all items can be freely estimated within the reference group but each corresponding intercept must be constrained to be equal across groups (i.e., $\tau^{(m)}=\tau^{(f)}$) . In our example, we freely estimates the intercepts for reading, writing, math and science for females but constrain males to have the same corresponding intercepts. We can think of scalar (strong) invariance as one that adds an additional constraint to the Metric Model, such that $$ \lambda^{(m)}_{ij} = \lambda^{(f)}_{ij}, \tau^{(m)}_{ij} = \tau^{(f)}_{ij}$$ for all $i,j$. Finally, since females are chosen to be the anchor, $\kappa^{(f)}=0$ and $\kappa^{(m)}$ is set free.
In order to fit the Scalar model in lavaan, recycle the same syntax as for the Metric model and add group.equal = c("loadings","intercepts"). As the syntax states, this allows for the loadings $\lambda$’s and the $\tau$’s to be the same across genders.
fit.Scalar <- cfa(onefac, data = hsbdemo, group = "female",
group.equal = c("loadings","intercepts"), meanstructure = TRUE)
summary(fit.Scalar , standardized=TRUE)
The output is presented below:
lavaan 0.6-8 ended normally after 108 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 25
Number of equality constraints 7
Number of observations per group:
female 109
male 91
Model Test User Model:
Test statistic 47.779
Degrees of freedom 10
P-value (Chi-square) 0.000
Test statistic for each group:
female 14.313
male 33.466
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Group 1 [female]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~
read 1.000 7.961 0.797
write (.p2.) 0.828 0.076 10.884 0.000 6.592 0.788
math (.p3.) 0.940 0.077 12.151 0.000 7.479 0.846
science (.p4.) 0.915 0.081 11.318 0.000 7.288 0.784
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read (.10.) 52.164 0.898 58.065 0.000 52.164 5.224
.write (.11.) 53.633 0.766 70.021 0.000 53.633 6.412
.math (.12.) 52.534 0.818 64.187 0.000 52.534 5.941
.science (.13.) 51.595 0.839 61.520 0.000 51.595 5.552
f1 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 36.315 6.399 5.675 0.000 36.315 0.364
.write 26.507 4.602 5.759 0.000 26.507 0.379
.math 22.251 4.545 4.896 0.000 22.251 0.285
.science 33.247 5.715 5.818 0.000 33.247 0.385
f1 63.376 11.894 5.328 0.000 1.000 1.000
Group 2 [male]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~
read 1.000 8.640 0.822
write (.p2.) 0.828 0.076 10.884 0.000 7.155 0.681
math (.p3.) 0.940 0.077 12.151 0.000 8.117 0.804
science (.p4.) 0.915 0.081 11.318 0.000 7.910 0.758
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read (.10.) 52.164 0.898 58.065 0.000 52.164 4.964
.write (.11.) 53.633 0.766 70.021 0.000 53.633 5.103
.math (.12.) 52.534 0.818 64.187 0.000 52.534 5.206
.science (.13.) 51.595 0.839 61.520 0.000 51.595 4.945
f1 0.152 1.272 0.119 0.905 0.018 0.018
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 35.798 7.935 4.512 0.000 35.798 0.324
.write 59.273 10.111 5.862 0.000 59.273 0.537
.math 35.924 7.495 4.793 0.000 35.924 0.353
.science 46.310 8.702 5.322 0.000 46.310 0.425
f1 74.649 14.704 5.077 0.000 1.000 1.000
Note now the addition of the labels (.10.), (.11.), (.12.), and (.13.) These parameters correspond to the observed intercepts for reading, writing, math and science respectively, constrained to be equal for both males and females ($52.1, 53.6, 52.3,$ and $51.6$). Just as we saw with the standardized loadings, the standardized intercepts under Std.all differ between genders due to the difference in standard deviations of the indicators. Finally, note the latent means, $\hat{\kappa}^{(f)}=0$ and $\hat{\kappa}^{(m)}=0.152$. If the Scalar model holds, then this implies that males have higher achievement than females. Since we have yet to test this assumption, this statement is yet to be verified.
Quiz
True or false. Scalar invariance is the first of the four fundamental models that allows comparisons in the latent construct across groups.
Answer: True.
True or false. In strong invariance, all observed intercepts must be constrained to be equal within a particular group.
Answer: False. The observed intercepts can be freely estimated and different from other intercepts within the reference group but respective intercepts must be constrained to be the same as that of the reference group for the other groups.
Residual (Strict) invariance
Scalar invariance constrains observed intercepts to be equal across groups and as the name implies, residual invariance further constrains the residual variances to be the same across groups. Residual or strict invariance is an assumption that is difficult to achieve in practice because it assumes that any unexplained variance not to due the factor is also equivalent across groups. Unexplained variance is by assumption unsystematic. For example, student performance on a particular day may be affected by situations such as student mood, the weather, or the test environment itself. These variables are not assumed to be equivalent across groups. The exception to this assumption is when systematic variance remains unexplained. For example, suppose the assessment was a mobile-based assessment and a secondary factor that explains performance may be familiarity of the student with mobile technology, but was unmeasured at the time of assessment. In such a case, the residual variance for each item may be an indirect measure of the systematic variance.
In formal notation, residual (strict) invariance further constrains the Scalar Model, such that
$$\lambda^{(m)}_{ij} = \lambda^{(f)}_{ij}, \tau^{(m)}_{ij} = \tau^{(f)}_{ij}, \theta^{\delta,(m)}_{ij} = \theta^{\delta,(f)}_{ij}$$
for all $i,j$. Just as females were chosen as the reference group in the Scalar model, we continue to set $\kappa^{(f)}=0$ and $\kappa^{(m)}$ to be free.
In order to fit the Residual model in lavaan, recycle the same syntax as for the Scalar model and add group.equal = c("loadings","intercepts","residuals"). As the syntax states, this allows for the loadings $\lambda$’s, $\tau$’s and $\theta_{\delta}$’s to be the same across genders.
fit.Residual <- cfa(onefac, data = hsbdemo, group = "female",
group.equal = c("loadings","intercepts","residuals"), meanstructure = TRUE)
summary(fit.Residual, standardized=TRUE)
The output is as follows:
lavaan 0.6-8 ended normally after 63 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 25
Number of equality constraints 11
Number of observations per group:
female 109
male 91
Model Test User Model:
Test statistic 61.218
Degrees of freedom 14
P-value (Chi-square) 0.000
Test statistic for each group:
female 34.340
male 26.878
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Group 1 [female]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~
read 1.000 7.824 0.792
write (.p2.) 0.853 0.079 10.828 0.000 6.672 0.727
math (.p3.) 0.928 0.077 11.988 0.000 7.258 0.805
science (.p4.) 0.924 0.082 11.293 0.000 7.233 0.756
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read (.10.) 52.215 0.887 58.889 0.000 52.215 5.286
.write (.11.) 52.762 0.799 66.038 0.000 52.762 5.747
.math (.12.) 52.631 0.814 64.629 0.000 52.631 5.837
.science (.13.) 51.836 0.844 61.405 0.000 51.836 5.418
f1 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read (.p5.) 36.370 5.172 7.033 0.000 36.370 0.373
.write (.p6.) 39.784 4.937 8.058 0.000 39.784 0.472
.math (.p7.) 28.606 4.235 6.754 0.000 28.606 0.352
.science (.p8.) 39.224 5.116 7.668 0.000 39.224 0.428
f1 61.213 11.511 5.318 0.000 1.000 1.000
Group 2 [male]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~
read 1.000 8.754 0.823
write (.p2.) 0.853 0.079 10.828 0.000 7.465 0.764
math (.p3.) 0.928 0.077 11.988 0.000 8.121 0.835
science (.p4.) 0.924 0.082 11.293 0.000 8.093 0.791
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read (.10.) 52.215 0.887 58.889 0.000 52.215 4.912
.write (.11.) 52.762 0.799 66.038 0.000 52.762 5.399
.math (.12.) 52.631 0.814 64.629 0.000 52.631 5.412
.science (.13.) 51.836 0.844 61.405 0.000 51.836 5.066
f1 0.032 1.269 0.026 0.980 0.004 0.004
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read (.p5.) 36.370 5.172 7.033 0.000 36.370 0.322
.write (.p6.) 39.784 4.937 8.058 0.000 39.784 0.417
.math (.p7.) 28.606 4.235 6.754 0.000 28.606 0.303
.science (.p8.) 39.224 5.116 7.668 0.000 39.224 0.375
f1 76.629 15.048 5.092 0.000 1.000 1.000
Note now the addition of the labels (.p5.), (.p6.), (.p7.), and (.p8.) These parameters correspond to the residual variances for reading, writing, math and science respectively, constrained to be equal for both males and females ($36.4, 39.8, 28.6,$ and $39.2$). Again, the standardized residual variances under Std.all differ between genders due to the difference in standard deviations of the indicators. Finally, the results show that holding the residual intercepts to be the same across groups, the additional increase in male student performance compared to females is now only $\hat{\kappa}^{(m)}=0.032$. But can we trust the results? Looking at the CFI below, we see that it is only $0.88$.
> fitMeasures(fit.Residual, "cfi") cfi 0.88
A recommended threshold for CFI is $0.95$ or higher, and compared to the CFI of $0.904$ for the Scalar model as shown below, the results suggest that residual invariance may not be a valid assumption for this particular set of data.
> fitMeasures(fit.Scalar, "cfi") cfi 0.904
Looking at the approximate fit indices gives us a clue about the plausibility of each of the four fundamental models, however an absolute test is needed to compare models to each other. In the following section we will show how to perform model comparisons using the chi-square difference test.
Quiz
True or false. The maximum CFI the scalar invariant model can achieve is the CFI of the metric invariant model.
Answer: True. Recall that the fit of subsequent models is at most no worse than the first model. Check this yourself using fitMeasures(fit.Metric, "cfi") where we get CFI=1.00 for the metric invariant model and compare to fitMeasures(fit.Scalar, "cfi") where we get CFI = 0.904 for the scalar invariant model.
True or false. Residual invariance is also called strict invariance because it constrains loadings, observed intercepts, residual variances, factor means and factor variances to be the same across groups.
Answer: False. Residual invariance allows factor means and variances to differ across groups.
Model fit comparisons of invariance models
The CFI can be a good way to quickly assess relative model fit comparisons. Some researchers (Cheung and Rensvold, 2002; Putnick and Bornstein, 2016) suggest that a CFI difference of 0.01 between two models is the threshold for claiming model deviations. In our example above, the CFI difference of the strong invariance and residual invariance model is $0.904-0.88=0.024$ which is above the threshold and suggests that there is a difference in the fit of these two models. However, since we do not know the true distribution of the CFI, we cannot make any inferential claims about statistical significance. Alternatively we may use chi-square difference testing, which allows us to make sample based inferences about the population. Recall the the null hypothesis in a typical CFA model is
$$H_0: \Sigma{(\theta)}=\Sigma$$
which means that the covariance matrix reproduced by the parameters equals the population covariance matrix (see Introduction to Structural Equation Modeling (SEM) in R with lavaan). Then the maximum likelihood fit function is described (Jöreskog; 1969, 2016)
$$F_{ML} = \log |\hat{\Sigma}(\theta)| + tr(S {\hat{\Sigma}}^{-1}(\theta))-\log|S|-(p+q)$$
where $|\cdot|$ is the determinant of the matrix, $tr$ indicates the trace or the sum of the diagonal elements, $\log$ is the natural log, $p$ is the number of exogenous variables, and $q$ is the number of endogenous variables. Under the null hypothesis, it can be assumed that
$$(N-1) F_{ML} \sim \chi^2(df)$$
which means that as sample size increases towards infinity, a function of the sample size times the fit function is chi-square distributed. The $(N-1) F_{ML}$ is also known as the Test Statistic under the Model Test User Model in lavaan summary output. In the case where there are two models where one model is nested in the other (BOLLEN, p.292), under regularity conditions described in Steiger (1985),
$$(N-1) F_{1} – (N-1) F_{0} = (N-1) (F_{1} – F_{0}) \sim \chi^2(df_1 – df_0)=\chi^2_{D}$$
A model in CFA is nested in a more unrestricted model if you can constrain parameters from the unrestricted model to obtain the more restricted one. Then the equation above means that for a sufficiently large sample, the difference of the two test statistics ($(N-1)F_{1}$ for the nested model and $(N-1)F_{0}$ for the more unrestricted) is distributed as a chi-square statistic with $df_1 – df_0$ degrees of freedom where $df_1$ is the number of free parameters in the nested model and $df_0$ is the number of free parameters in the more unrestricted model. The two models together are known as a hierarchical model.
Much like chi-square fit testing, chi-square difference testing for hierarchical models in CFA/SEM is an accept-support test (Bollen, 2016); which means that the desired hypothesis is the null rather than the alternative. For a test of the difference of two models, the null hypothesis is that the unrestricted model and the nested model are the same, known as the equal fit hypothesis. A rejection of the equal fit hypothesis means that the unrestricted and nested models are different, which means that the unrestricted model is preferred. The goal is to achieve a nested model that is just as good as the unrestricted one, but one with more parsimony and larger degrees of freedom.
To conduct a chi-square difference test in lavaan, use the function lavTestLRT() where the parameters are two or more lavaan model objects. If more than two parameters are supplied, the output will report sequential tests of the current model against the more unrestricted one. Let’s look at an example where we test all models (configural, metric, scalar, and residual) invariance simultaneously, corresponding to fit.Configural, fit.Metric, fit.Scalar, and fit.Residual.
> lavTestLRT(fit.Configural, fit.Metric, fit.Scalar, fit.Residual)
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
fit.Configural 4 5526.0 5605.2 2.622
fit.Metric 7 5524.2 5593.5 6.801 4.179 3 0.24277
fit.Scalar 10 5559.2 5618.6 47.779 40.978 3 6.609e-09 ***
fit.Residual 14 5564.6 5610.8 61.218 13.439 4 0.00932 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
The output reports sequential chi-square difference tests of the current model against the preceding more unrestricted model. Since fit.Configural is the most unrestricted model, the first row only reports the Model chi-square under Chisq and nothing under Chisq diff. You can verify that indeed it is the same as the overall (not split by each group) Test statistic for the Configural Model.
Model Test User Model:
Test statistic 2.622
Degrees of freedom 4
P-value (Chi-square) 0.623
Test statistic for each group:
female 1.903
male 0.719
The row fit.Metric is the first proper chi-square difference test, taking the difference of the chi-square for Metric model and that of the Configural model, $6.801 – 2.622 = 4.179$. As shown in the Df diff column, the difference in degrees of freedom is $7-4=3$. The p-value is $0.243$ which means we fail to reject the null hypothesis and verify the equal fit hypothesis that the Metric model is no worse than the Configural model. To manually verify the p-value, use the pchisq() function in R, which obtains the cumulative probability $P(X \le x)$ of the quantile $x=4.179$ for the chi-square distribution with $3$ degrees of freedom. However, since our rejection rejection is $x > 4.179$ we specify lower.tail=FALSE.
> pchisq(q=4.179,df=3,lower.tail=FALSE) [1] 0.2427728
The next sequential test is comparing the more unrestricted Metric model to the nested Scalar model. Note here that the p-value is less than $0.05$ (given our $\alpha=0.05$), so we reject the null hypothesis and fail to verify the equal fit hypothesis. This suggests that the Scalar model and Metric models are different, and therefore Scalar invariance fails and we cannot make the claim that male students have higher achievement than females. Finally, since Scalar invariance failed we cannot proceed further and we also cannot claim Residual invariance. In conclusion, we can make claims that the two tests measure the same latent construct of achievement between male and female students (supported metric invariance), but we have not obtained sufficient evidence that we can compare the levels of achievement between the two genders (failed scalar and residual invariance).
Quiz
True or false. The row fit.Scalar in the output above compares the Scalar model to the Configural model.
Answer: False. Chi-square difference testing in measurement invariance should be sequential, so that the more unrestricted model (Metric) should be compared to the more restricted model (Scalar). You can verify that the degrees of freedom difference under the Df diff column is 10-7=3 and not 10-4=6.
True or false. The unrestricted model has less degrees of freedom compared to the nested model.
Answer: True. The unrestricted model has more free parameters to estimate so less degrees of freedom compared to the nested model. You can verify that the degrees of freedom for the Configural model is 4 whereas it is 7 for the Metric model. See the section on Known values, parameters, and degrees of freedom in the Confirmatory Factor Analysis (CFA) in R with lavaan seminar for more information about the relationship of free parameters and degrees of freedom.
Partial invariance
In theory, once configural variance is established, measurement invariance implies that all loadings in a given factor are equal across groups. In practice however, this may be difficult to achieve especially if the ratio of items to factors is high. The more items in a particular factor, the more likely at least one of the items will not satisfy metric invariance. A more realistic situation is to expect that most of the loadings are equal across groups with exception of a few that may deviate; this is known as partial invariance. Partial invariance can be established for metric, scalar or residual invariance, but is most commonly seen in metric invariance.
In our example, although we previously established metric invariance across gender, suppose we assume partial invariance where reading scores are expected to deviate between male and female students. As we have in the section lavaan syntax cheatsheet, in order to specify a different parameters across two groups we need to specify c(a,b)* in front of the item we wish to unconstrain across groups. The first letter a indicates a free parameter labeled ‘a’ in the first group, and second letter b indicates that the paramater that is different from ‘a’ but also freely estimated. We continue to estimate the observed intercepts of each item with ~1 and group.equal = c("loadings") tells lavaan that we want to model metric invariance.
onefac_d <- 'f1 =~ read + write + c(a,b)*math + science
read ~ 1
write ~ 1
math ~ 1
science ~ 1'
fit.Partial <- cfa(onefac_d, data = hsbdemo, group = "female",
group.equal = c("loadings"), meanstructure = TRUE)
summary(fit.Partial, standardized=TRUE)
The output is as follows:
lavaan 0.6-8 ended normally after 82 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 24
Number of equality constraints 2
Number of observations per group:
female 109
male 91
Model Test User Model:
Test statistic 3.833
Degrees of freedom 6
P-value (Chi-square) 0.699
Test statistic for each group:
female 2.512
male 1.321
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Group 1 [female]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~
read 1.000 7.589 0.778
write (.p2.) 0.872 0.074 11.750 0.000 6.614 0.805
math (a) 1.037 0.100 10.363 0.000 7.869 0.864
science (.p4.) 0.932 0.080 11.613 0.000 7.070 0.778
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 51.734 0.934 55.367 0.000 51.734 5.303
.write 54.991 0.787 69.846 0.000 54.991 6.690
.math 52.394 0.872 60.052 0.000 52.394 5.752
.science 50.697 0.870 58.244 0.000 50.697 5.579
f1 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 37.568 6.329 5.936 0.000 37.568 0.395
.write 23.818 4.240 5.617 0.000 23.818 0.353
.math 21.045 4.722 4.457 0.000 21.045 0.254
.science 32.595 5.495 5.932 0.000 32.595 0.395
f1 57.595 11.107 5.185 0.000 1.000 1.000
Group 2 [male]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~
read 1.000 8.950 0.835
write (.p2.) 0.872 0.074 11.750 0.000 7.800 0.776
math (b) 0.820 0.098 8.331 0.000 7.340 0.764
science (.p4.) 0.932 0.080 11.613 0.000 8.338 0.790
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 52.824 1.123 47.034 0.000 52.824 4.931
.write 50.121 1.053 47.584 0.000 50.121 4.988
.math 52.945 1.008 52.548 0.000 52.945 5.508
.science 53.231 1.106 48.113 0.000 53.231 5.044
f1 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.read 34.682 7.698 4.505 0.000 34.682 0.302
.write 40.120 7.568 5.302 0.000 40.120 0.397
.math 38.503 7.246 5.313 0.000 38.503 0.417
.science 41.868 8.129 5.150 0.000 41.868 0.376
f1 80.101 15.766 5.081 0.000 1.000 1.000
We can see in the output above as expected that the loadings for writing (.p2.) and science (.p4.) are constrained to be the same across genders, whereas for the loading for math, (a), (b) differs between genders. [FINISH adding standardized loadings]
> lavTestLRT(fit.Configural, fit.Partial)
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
fit.Configural 4 5526.0 5605.2 2.6220
fit.Partial 6 5523.3 5595.8 3.8335 1.2115 2 0.5457
Exercise 3A
Suppose that the researcher was interested in establishing partial invariance removing the constraint of reading across genders instead of math. Look at the output and see if the constraints are correctly specified. If not, explain why.
Answer:
As we know from Confirmatory Factor Analysis (CFA) in R with lavaan, by default lavaan uses marker method for identification. The marker method is independent of the constraints for metric invariance, but in this case they are conflated, leading the output to constrain the loadings for reading when the researcher wanted to have them unconstrained.
Without too much thought into identification, the (incorrect) lavaan code would be:
onefac_c <- 'f1 =~ c(a,b)*read + write + math + science
read ~ 1
write ~ 1
math ~ 1
science ~ 1'
fit.Partial2 <- cfa(onefac_c, data = hsbdemo, group = "female",
group.equal = c("loadings"), meanstructure = TRUE)
summary(fit.Partial2, standardized=TRUE)
The abbreviated output looks like:
Group 1 [female]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~
read (a) 1.000 7.844 0.790
write (.p2.) 0.866 0.074 11.744 0.000 6.789 0.816
math (.p3.) 0.939 0.077 12.214 0.000 7.365 0.836
science (.p4.) 0.928 0.080 11.590 0.000 7.277 0.790
Group 2 [male]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~
read (b) 1.000 8.664 0.822
write (.p2.) 0.866 0.074 11.744 0.000 7.498 0.760
math (.p3.) 0.939 0.077 12.214 0.000 8.134 0.803
science (.p4.) 0.928 0.080 11.590 0.000 8.037 0.775
Exercise 3B (Challenge)
Try to rewrite the lavaan syntax above to solve the marker method problem. Pick another item such as writing to serve as the marker instead. Also, what is an alternative solution to the marker method problem?
Hint: use NA and auto.fix.first = FALSE
Answer:
The specification we used above c(c,d)*read does not work in this case because the first item (reading) by default is set to 1. First, we need to turn off the default in the cfa() function using auto.fix.first = FALSE. Second, we need to play around with the model syntax for multigroup models. Recall that NA* frees the parameter if it was previously fixed. Since we need to free the same parameter across both groups the solution is thus c(NA,NA)*read. Finally, although we correctly specified partial invariance, we need to still identify the CFA model itself using marker method. We choose the writing item, and specify c(1,1)*write which tells lavaan that we want to constrain the loading of the writing item at 1 for both males and females.
onefac_e <- 'f1 =~ c(NA,NA)*read + c(1,1)*write + math + science
read ~ 1
write ~ 1
math ~ 1
science ~ 1'
fit.Partial3 <- cfa(onefac_e, data = hsbdemo, group = "female",
group.equal = c("loadings"), meanstructure = TRUE, auto.fix.first = FALSE)
summary(fit.Partial3, standardized=TRUE)
You will notice in the output below that the writing item now serves as the marker, and reading is now unconstrained across genders, which is what we expect.
Group 1 [female]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~
read (.p1.) 1.155 0.098 11.744 0.000 7.844 0.790
write 1.000 6.789 0.816
math (.p3.) 1.085 0.090 12.073 0.000 7.365 0.836
science (.p4.) 1.072 0.094 11.452 0.000 7.277 0.790
Group 2 [male]:
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~
read (.p1.) 1.155 0.098 11.744 0.000 8.664 0.822
write 1.000 7.498 0.760
math (.p3.) 1.085 0.090 12.073 0.000 8.134 0.803
science (.p4.) 1.072 0.094 11.452 0.000 8.037 0.775
Alternatively, instead of identification through marker method, we can identify the CFA model through variance standardization, which would eliminate the conflated identification problem. The variance standardization method is left as an exercise for the reader. Refer to the section Variance standardization in metric invariance for more information.
References
Acock, A. C. (2013). Discovering structural equation modeling using Stata. Stata Press Books.
Bollen, K. A. (1989). Structural equations with latent variables (Vol. 210). John Wiley & Sons.
Cheung, G. W., & Rensvold, R. B. (2002). Evaluating goodness-of-fit indexes for testing measurement invariance. Structural equation modeling, 9(2), 233-255.
Gregorich, S. E. (2006). Do self-report instruments allow meaningful comparisons across diverse population groups? Testing measurement invariance using the confirmatory factor analysis framework. Medical care, 44(11 Suppl 3), S78.
Hox, J. J., Moerbeek, M., & Van de Schoot, R. (2017). Multilevel analysis: Techniques and applications. Routledge.
Joreskog, K. G. (1969). A general approach to confirmatory maximum likelihood factor analysis. Psychometrika.
Jöreskog, K. G., Olsson, U. H., & Wallentin, F. Y. (2016). Multivariate analysis with LISREL. Basel, Switzerland: Springer.
Kline, R. B. (2016). Principles and practice of structural equation modeling (4th ed.). Guilford publications.
Pavlov, G., Shi, D., & Maydeu-Olivares, A. (2020). Chi-square difference tests for comparing nested models: An evaluation with non-normal data. Structural Equation Modeling: A Multidisciplinary Journal, 27(6), 908-917.
Putnick, D. L., & Bornstein, M. H. (2016). Measurement invariance conventions and reporting: The state of the art and future directions for psychological research. Developmental review, 41, 71-90.
Raudenbush, S. W., & Bryk, A. S. (2002). Hierarchical linear models: Applications and data analysis methods (Vol. 1). Sage.
Singer, J. D. (1998). Using SAS PROC MIXED to fit multilevel models, hierarchical models, and individual growth models. Journal of educational and behavioral statistics, 23(4), 323-355.
Steiger, J. H., Shapiro, A., & Browne, M. W. (1985). On the multivariate asymptotic distribution of sequential chi-square statistics. Psychometrika, 50(3), 253-263.
Yves Rosseel (2012). lavaan: An R Package for Structural Equation Modeling. Journal of Statistical Software, 48(2), 1-36. URL http://www.jstatsoft.org/v48/i02/.
Links direct from the authors of lavaan
lavaan‘s multipgroup page https://lavaan.ugent.be/tutorial/groups.htmllavaan‘s growth model page https://lavaan.ugent.be/tutorial/growth.html
Mplus discussion board on standardized loadings not being equal across measurement invariance models
Lesa Hoffman’s excellent slides on CFA and measurement invariance (she uses variance standardization method instead of marker method)