Version info: Code for this page was tested in SAS 9.3
Zero-truncated poisson regression is used to model count data for which the value zero cannot occur.
Please Note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and verification, verification of assumptions, model diagnostics and potential follow-up analyses.
Examples of zero-truncated Poisson regression
Example 1.
A study of length of hospital stay, in days, as a function of age, kind of health insurance and whether or not the patient died while in the hospital. Length of hospital stay is recorded as a minimum of at least one day.
Example 2.
A study of the number of journal articles published by tenured faculty as a function of discipline (fine arts, science, social science, humanities, medical, etc). To get tenure faculty must publish, therefore, there are no tenured faculty with zero publications.
Example 3.
A study by the county traffic court on the number of tickets received by teenagers as predicted by school performance, amount of driver training and gender. Only individuals who have received at least one citation are in the traffic court files.
Description of the data
Let’s pursue Example 1 from above.
We have a hypothetical data file, ztp, with 1,493 observations available: ztp . The length of hospital stay variable is stay. The variable age gives the age group from 1 to 9 which will be treated as interval in this example. The variables hmo and died are binary indicator variables for HMO insured patients and patients who died while in the hospital, respectively.
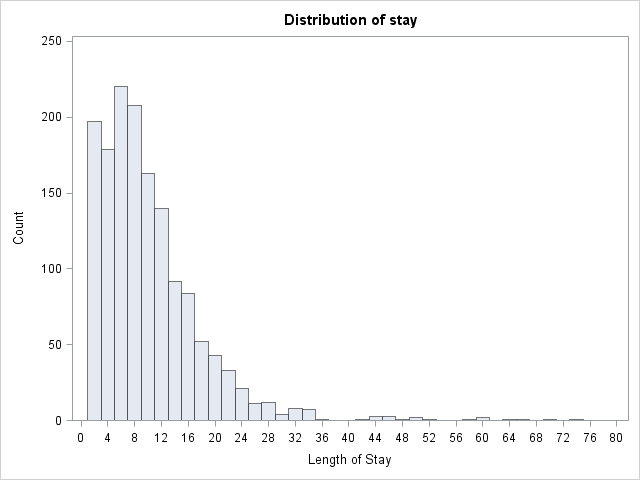
Let’s look at the data.
proc means data=mylib.ztp;
var stay;
run;
The MEANS Procedure
Analysis Variable : stay Length of Stay
N Mean Std Dev Minimum Maximum
--------------------------------------------------------------------
1493 9.7287341 8.1329081 1.0000000 74.0000000
--------------------------------------------------------------------
proc univariate data=mylib.ztp noprint;
histogram stay / midpoints = 0 to 80 by 2 vscale = count;
run;
proc freq data=mylib.ztp;
tables age hmo died;
run;
The FREQ Procedure
Age Group
Cumulative Cumulative
age Frequency Percent Frequency Percent
--------------------------------------------------------
1 6 0.40 6 0.40
2 60 4.02 66 4.42
3 163 10.92 229 15.34
4 291 19.49 520 34.83
5 317 21.23 837 56.06
6 327 21.90 1164 77.96
7 190 12.73 1354 90.69
8 93 6.23 1447 96.92
9 46 3.08 1493 100.00
hmo
Cumulative Cumulative
hmo Frequency Percent Frequency Percent
--------------------------------------------------------
0 1254 83.99 1254 83.99
1 239 16.01 1493 100.00
died
Cumulative Cumulative
died Frequency Percent Frequency Percent
---------------------------------------------------------
0 981 65.71 981 65.71
1 512 34.29 1493 100.00
Analysis methods you might consider
Below is a list of some analysis methods you may have encountered. Some of the methods listed are quite reasonable while others have either fallen out of favor or have limitations.
- Zero-truncated Poisson Regression – The focus of this web page.
- Zero-truncated Negative Binomial Regression – If you have overdispersion in addition to zero truncation. See the Data Analysis Example for ztnb.
- Poisson Regression – Ordinary Poisson regression will have difficulty with zero-truncated data. It will try to predict zero counts even though there are no zero values.
- Negative Binomial Regression – Ordinary Negative Binomial regression will have difficulty with zero-truncated data. It will try to predict zero counts even though there are no zero values.
- OLS Regression – You could try to analyze these data using OLS regression. However, count data are highly non-normal and are not well estimated by OLS regression.
Zero-truncated Poisson regression using proc nlmixed
In order to use proc nlmixed to perform truncated Poisson regression, we must supply it with a likelihood function.
The probability that an observation has count \(y\) under the Poisson distribution (without zero truncation) is given by the equation: $$P(Y=y) = \frac{\lambda^y e^{-\lambda}}{y!}$$
With zero truncation, we calculate the probability that \(Y=y\) conditional on \(Y>0\), that is, that \(Y\) is observed as 0 values are not observed. Thus: $$P(Y=y|Y>0) = \frac{P(Y=y)}{P(Y>0)} = \frac{P(Y=y)}{1-P(Y=0)} = \frac{\lambda^y e^{-\lambda}}{y!(1-e^{-\lambda})}$$
The log-likelihood function for the zero-truncated Poisson distribution is then:
$$\mathcal{L}=\sum\limits_{i=1}^n[y_ilog(\lambda) – \lambda – log(1 – e^{-\lambda}) – log(y_i!)]$$
In Poisson regression, we model (log(lambda)), the log of the expected counts, as a linear combination of a set of predictors:
$$log(\lambda) = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3$$
We supply the last two equations to proc nlmixed to model our data using a zero truncated Poisson distribution. Additionally, proc nlmixed does not support a class statement, so categorical variables should be dummy-coded before running the analysis.
proc nlmixed data = mylib.ztp;
log_lambda = intercept + b_age*age + b_died*died + b_hmo*hmo;
lambda = exp(log_lambda);
ll = stay*log_lambda - lambda - log(1-exp(-lambda)) - lgamma(stay+1);
model stay ~ general(ll);
run;
The NLMIXED Procedure
Specifications
Data Set MYLIB.ZTP
Dependent Variable stay
Distribution for Dependent Variable General
Optimization Technique Dual Quasi-Newton
Integration Method None
Dimensions
Observations Used 1493
Observations Not Used 0
Total Observations 1493
Parameters 4
Parameters
intercept b_age b_died b_hmo NegLogLike
1 1 1 1 6176595.73
Iteration History
Iter Calls NegLogLike Diff MaxGrad Slope
1 9 21118.0877 6155478 145098.1 -2.38E13
2 12 18578.3704 2539.717 137452.3 -436416
3 14 18437.2943 141.0761 120107 -13864.4
4 16 18394.0864 43.20793 118005.9 -3700.37
5 18 17809.511 584.5754 126017.3 -788.358
6 20 12597.6045 5211.906 71574.7 -383.804
7 21 7312.74337 5284.861 7488.696 -3740.01
8 23 7029.45115 283.2922 684.374 -459.944
9 25 6943.66162 85.78953 2049.627 -98.7188
10 27 6911.69968 31.96194 1391.058 -53.8698
11 29 6909.12237 2.577317 98.24019 -4.28966
12 31 6908.81335 0.309012 23.25771 -0.33228
13 33 6908.80066 0.012691 29.08574 -0.01855
14 35 6908.79908 0.001588 0.573832 -0.00203
15 37 6908.79907 3.373E-6 0.019132 -6.95E-6
NOTE: GCONV convergence criterion satisfied.
The SAS System 09:40 Tuesday, May 29, 2012 2
The NLMIXED Procedure
Fit Statistics
-2 Log Likelihood 13818
AIC (smaller is better) 13826
AICC (smaller is better) 13826
BIC (smaller is better) 13847
Parameter Estimates
Standard
Parameter Estimate Error DF t Value Pr > |t| Alpha Lower Upper Gradient
intercept 2.4358 0.02733 1493 89.12 <.0001 0.05 2.3822 2.4894 0.003988
b_age -0.01444 0.005035 1493 -2.87 0.0042 0.05 -0.02432 -0.00457 0.019132
b_died -0.2038 0.01837 1493 -11.09 <.0001 0.05 -0.2398 -0.1677 0.000506
b_hmo -0.1359 0.02374 1493 -5.72 <.0001 0.05 -0.1825 -0.08933 -0.00231
The output looks very much like the output from an OLS regression:
- Towards the top is the iteration history, giving the values of the log pseudolikelihoods.
- The last value in the log (-6908.7990731) is the final value of the log pseudolikelihood for the full model.
- Next comes a number of fit statistics, which can be used to compare the fit of nested models.
- Below the fit statistics are the zero-truncated poisson coefficients for each of the variables along with standard errors, t-scores, and p-values.
Looking through the results we see the following:
- The value of the coefficient for age, -.01444, suggests that the log count of stay decreases by .01444 for each year increase in age. This coefficient is statistically significant.
- The coefficient for hmo, -.1359, is significant and indicates that the log count of stay for HMO patient is .1359 less than for non-HMO patients.
- The log count of stay for patients who died while in the hospital was .20377 less than those of patients who did not die.
- Finally, the value of the constant (intercept), 2..4358 is log count of the stay when age = 0, hmo = 0, and died = 0.
We can also use estimate statments to help understand our model. For example we can predict the expected number of days spent at the hospital across age groups for the two hmo statuses for patients who died. The estimate statement for proc nlmixed works slightly differently from how it works within other procs. Here, each parameter must be explicitly multiplied by the value at which is to be held for that estimate statment. Additionally, because we would like to predict actual number of days rather than log number of days, we need to exponentiate the estimate.
proc nlmixed data = mylib.ztp;
log_lambda = intercept + b_age*age + b_died*died + b_hmo*hmo;
lambda = exp(log_lambda);
ll = stay*log_lambda - lambda - log(1-exp(-lambda)) - lgamma(stay+1);
model stay ~ general(ll);
estimate 'age 1 died 1 hmo 0' exp(intercept * 1 + b_age * 1 + b_died * 1 + b_hmo * 0);
estimate 'age 1 died 1 hmo 1' exp(intercept * 1 + b_age * 1 + b_died * 1 + b_hmo * 1);
estimate 'age 3 died 1 hmo 0' exp(intercept * 1 + b_age * 3 + b_died * 1 + b_hmo * 0);
estimate 'age 3 died 1 hmo 1' exp(intercept * 1 + b_age * 3 + b_died * 1 + b_hmo * 1);
estimate 'age 5 died 1 hmo 0' exp(intercept * 1 + b_age * 5 + b_died * 1 + b_hmo * 0);
estimate 'age 5 died 1 hmo 1' exp(intercept * 1 + b_age * 5 + b_died * 1 + b_hmo * 1);
estimate 'age 7 died 1 hmo 0' exp(intercept * 1 + b_age * 7 + b_died * 1 + b_hmo * 0);
estimate 'age 7 died 1 hmo 1' exp(intercept * 1 + b_age * 7 + b_died * 1 + b_hmo * 1);
estimate 'age 9 died 1 hmo 0' exp(intercept * 1 + b_age * 9 + b_died * 1 + b_hmo * 0);
estimate 'age 9 died 1 hmo 1' exp(intercept * 1 + b_age * 9 + b_died * 1 + b_hmo * 1);
run;
<**SOME OUTPUT OMITTED**>
Additional Estimates
Standard
Label Estimate Error DF t Value Pr > |t| Alpha Lower Upper
age 1 died 1 hmo 0 9.1852 0.2548 1493 36.05
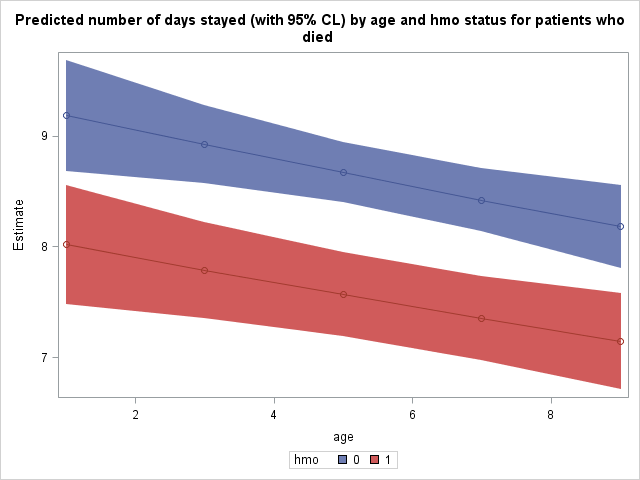
We can see that the number of days spent tends to decrease as we move up age groups and that patients enrolled in an hmo (hmo = 1) tend to spend fewer days at the hospital as well than those not in hmos. For example, we expect that a non-hmo patient who died in age group 1 to stay for 9.1852 days whereas an hmo patient who died in age group 1 is expected to stay 8.0180 days.
It may be illustrative for us to plot the predicted number of days stayed as a function of age and hmo status. To do this, we must tell SAS to save this table of predicted values as a dataset. Tables and graphics produced by procedures are given names upon creation. We will need the name of this prediction table to tell SAS to save it. Place ods trace on and ods trace off statements around the procedure which produced this table to obtain its name. Output from the ods trace statements is located in the log, not the output.
ods trace on;
proc nlmixed data = mylib.ztp;
log_lambda = intercept + b_age*age + b_died*died + b_hmo*hmo;
lambda = exp(log_lambda);
ll = stay*log_lambda - lambda - log(1-exp(-lambda)) - lgamma(stay+1);
model stay ~ general(ll);
estimate 'age 1 died 1 hmo 0' exp(intercept * 1 + b_age * 1 + b_died * 1 + b_hmo * 0);
estimate 'age 1 died 1 hmo 1' exp(intercept * 1 + b_age * 1 + b_died * 1 + b_hmo * 1);
estimate 'age 3 died 1 hmo 0' exp(intercept * 1 + b_age * 3 + b_died * 1 + b_hmo * 0);
estimate 'age 3 died 1 hmo 1' exp(intercept * 1 + b_age * 3 + b_died * 1 + b_hmo * 1);
estimate 'age 5 died 1 hmo 0' exp(intercept * 1 + b_age * 5 + b_died * 1 + b_hmo * 0);
estimate 'age 5 died 1 hmo 1' exp(intercept * 1 + b_age * 5 + b_died * 1 + b_hmo * 1);
estimate 'age 7 died 1 hmo 0' exp(intercept * 1 + b_age * 7 + b_died * 1 + b_hmo * 0);
estimate 'age 7 died 1 hmo 1' exp(intercept * 1 + b_age * 7 + b_died * 1 + b_hmo * 1);
estimate 'age 9 died 1 hmo 0' exp(intercept * 1 + b_age * 9 + b_died * 1 + b_hmo * 0);
estimate 'age 9 died 1 hmo 1' exp(intercept * 1 + b_age * 9 + b_died * 1 + b_hmo * 1);
run;
ods trace off;
<***SOME OF THE LOG OMITTED***>
Output Added:
-------------
Name: AdditionalEstimates
Label: Additional Estimates
Template: Stat.NLM.AdditionalEstimates
Path: Nlmixed.AdditionalEstimates
-------------
NOTE: PROCEDURE NLMIXED used (Total process time):
real time 0.20 seconds
cpu time 0.12 seconds
140 ods trace off;
Towards the end of the log we find the name of this table, which as expected by its heading in the output above, is “AdditionalEstimates”. We can now tell SAS to save this output table as the dataset “mylib.addest” using an ods output statement.
ods output AdditionalEstimates = mylib.addest;
proc nlmixed data = mylib.ztp;
log_lambda = intercept + b_age*age + b_died*died + b_hmo*hmo;
lambda = exp(log_lambda);
ll = stay*log_lambda - lambda - log(1-exp(-lambda)) - lgamma(stay+1);
model stay ~ general(ll);
estimate 'age 1 died 1 hmo 0' exp(intercept * 1 + b_age * 1 + b_died * 1 + b_hmo * 0);
estimate 'age 1 died 1 hmo 1' exp(intercept * 1 + b_age * 1 + b_died * 1 + b_hmo * 1);
estimate 'age 3 died 1 hmo 0' exp(intercept * 1 + b_age * 3 + b_died * 1 + b_hmo * 0);
estimate 'age 3 died 1 hmo 1' exp(intercept * 1 + b_age * 3 + b_died * 1 + b_hmo * 1);
estimate 'age 5 died 1 hmo 0' exp(intercept * 1 + b_age * 5 + b_died * 1 + b_hmo * 0);
estimate 'age 5 died 1 hmo 1' exp(intercept * 1 + b_age * 5 + b_died * 1 + b_hmo * 1);
estimate 'age 7 died 1 hmo 0' exp(intercept * 1 + b_age * 7 + b_died * 1 + b_hmo * 0);
estimate 'age 7 died 1 hmo 1' exp(intercept * 1 + b_age * 7 + b_died * 1 + b_hmo * 1);
estimate 'age 9 died 1 hmo 0' exp(intercept * 1 + b_age * 9 + b_died * 1 + b_hmo * 0);
estimate 'age 9 died 1 hmo 1' exp(intercept * 1 + b_age * 9 + b_died * 1 + b_hmo * 1);
run;
Now we can use this predicted values for plotting. We need to add actual values of age and hmo to the dataset for plotting as well.
data mylib.addest; set mylib.addest; input age hmo; datalines; 1 0 1 1 3 0 3 1 5 0 5 1 7 0 7 1 9 0 9 1 ; run;
Finally, we use proc sgplot to plot our predicted number of days stayed as well as 95% confidence interval bands. The predicted values, lines connecting them, and confidence interval bands are all specified separately within the same proc sgplot. The group option will produce separate points, lines, and bands by the grouping variable.
proc sgplot data = mylib.addest; title 'Predicted number of days stayed (with 95% CL) by age and hmo status for patients who died'; band x = age lower = lower upper = upper / group=hmo; scatter x= age y = estimate / group = hmo; series x = age y = estimate / group = hmo; run;
Zero-truncated Poisson regression using proc fmm
As of SAS 9.3, you can use proc fmm to fit zero-truncated Poisson models. You simply specify “dist = truncpoisson” in the model statement.
Although compared to proc nlmixed, proc fmm provides a much easier way to specify a zero-truncated poisson regression, it has much more limited postestimation options. For example, estimate and predict statements are not available with proc fmm. Additionally, proc fmm like most other SAS procs, uses the last group within a categorical variable as the reference group.
proc fmm data = mylib.ztp;
class hmo died;
model stay = age hmo died / dist = truncpoisson;
run;
The FMM Procedure
Model Information
Data Set MYLIB.ZTP
Response Variable stay
Type of Model Homogeneous Regression Mixture
Distribution Truncated Poisson
Components 1
Link Function Log
Estimation Method Maximum Likelihood
Class Level Information
Class Levels Values
hmo 2 0 1
died 2 0 1
Number of Observations Read 1493
Number of Observations Used 1493
Optimization Information
Optimization Technique Dual Quasi-Newton
Parameters in Optimization 4
Mean Function Parameters 4
Scale Parameters 0
Number of Threads 4
Iteration History
Objective Max
Iteration Evaluations Function Change Gradient
0 5 7444.776354 . 4192.321
1 4 6918.2708098 526.50554412 359.7548
2 4 6913.2026998 5.06811003 327.6266
3 4 6913.0538752 0.14882461 320.7117
4 4 6910.8911491 2.16272613 145.0423
5 3 6908.8042839 2.08686512 9.443069
6 3 6908.7990735 0.00521050 0.07041
7 3 6908.7990731 0.00000040 0.000569
Convergence criterion (GCONV=1E-8) satisfied.
The SAS System 09:48 Thursday, May 24, 2012 14
The FMM Procedure
Fit Statistics
-2 Log Likelihood 13817.6
AIC (smaller is better) 13825.6
AICC (smaller is better) 13825.6
BIC (smaller is better) 13846.8
Pearson Statistic 9968.8
Parameter Estimates for 'Truncated Poisson' Model
Standard
Effect hmo died Estimate Error z Value Pr > |z|
Intercept 2.0961 0.03766 55.65
Things to consider
- Count data often use exposure variable to indicate the number of times the event could have happened. You can incorporate exposure into your model by including a log-linear term for exposure in the log-likehood function specification.
- It is not recommended that zero-truncated poisson models be applied to small samples. What constitutes a small sample does not seem to be clearly defined in the literature.
- Pseudo-R-squared values differ from OLS R-squareds, please see FAQ: What are pseudo R-squareds? for a discussion on this issue.
References
- Cameron, A. Colin and Trivedi, P.K. (2009) Microeconometrics using stata. College Station, TX: Stata Press.
- Long, J. Scott, & Freese, Jeremy (2006). Regression Models for Categorical Dependent Variables Using Stata (Second Edition). College Station, TX: Stata Press.
- Long, J. Scott (1997). Regression Models for Categorical and Limited Dependent Variables. Thousand Oaks, CA: Sage Publications.