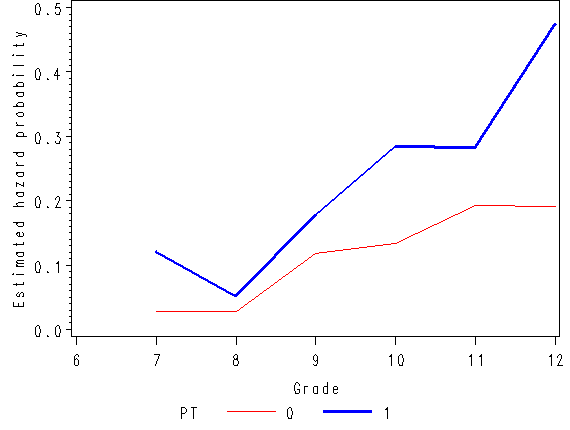
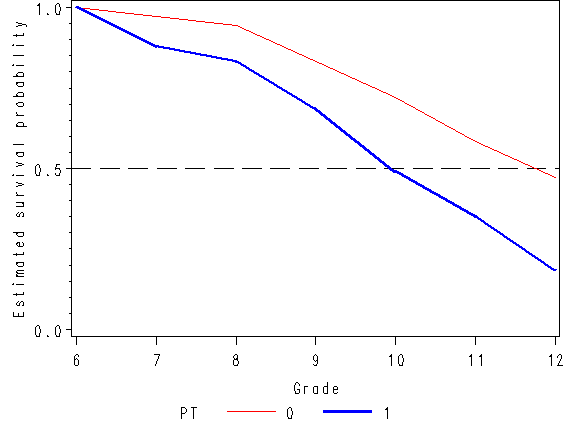
Figure 11.1, page 359
proc sort data = 'c:\alda\firstsex';
by pt;
run;
proc lifetest data = 'c:\alda\firstsex';
time time*censor(1);
by pt;
ods output ProductLimitEstimates = tsex;
run;
data fig11_1b;
set tsex (where = (survival~=.));
if time = 0 then time = 6;
lags = lag(survival);
by pt;
if ~ first.pt then do;
hazard = 1 - survival/lags;
end;
keep survival hazard time pt;
run;
goptions reset=all device=gif570;
symbol1 c=red i=join;
symbol2 c=blue i=join width=2;
axis1 order=(0 to .5 by 0.1) label=(a=90 'Estimated hazard probability');
axis2 order = (0 to 1 by .5) label=(a=90 'Estimated survival probability');
axis3 order = (6 to 12 by 1) minor = none label=('Grade');
proc gplot data=fig11_1b;
format time 2.0 survival hazard 3.1;
plot hazard*time = pt / vaxis=axis1 haxis=axis3;
plot survival*time = pt / vaxis=axis2 haxis=axis3 vref=0.5 lvref=21;
run;
quit;
Table 11.1, page 360. We will do create the table in two parts. The first part is based on the result from previous example. The data set tsex came from proc lifetest from previous example.
options nocenter nodate; data table11_1by_pt; set tsex (where = (survival~=.)); format left 4.0; myleft = lag(left); myfail = lag(failed); if time = 0 then time = 6; lags = lag(survival); by pt; if ~ first.pt then do; failed = failed - myfail; hazard = 1 - survival/lags; end; keep survival hazard time pt myleft failed; run;
proc print data = table11_1by_pt noobs; where hazard ~=.; format time 3.0; var time myleft failed hazard survival; run;
TIME myleft Failed hazard Survival
7 72 2 0.02778 0.9722 8 70 2 0.02857 0.9444 9 68 8 0.11765 0.8333 10 60 8 0.13333 0.7222 11 52 10 0.19231 0.5833 12 42 8 0.19048 0.4722 7 108 13 0.12037 0.8796 8 95 5 0.05263 0.8333 9 90 16 0.17778 0.6852 10 74 21 0.28378 0.4907 11 53 15 0.28302 0.3519 12 38 18 0.47368 0.1852
Now, we will create the part of Table 11.1 for overall survival regardless the parenting transitions.
proc lifetest data = alda.firstsex; time time*censor(1); ods output ProductLimitEstimates = tall; run; data table11_1all; set tall (where = (survival~=.)); format left 4.0; myleft = lag(left); myfail = lag(failed); if time = 0 then time = 6; lags = lag(survival); failed = failed - myfail; hazard = 1 - survival/lags; keep survival hazard time pt myleft failed; run; proc print data = table11_1all noobs; where hazard ~=.; format time 3.0; var time myleft failed hazard survival; run;
TIME myleft Failed hazard Survival
7 180 15 0.08333 0.9167 8 165 7 0.04242 0.8778 9 158 24 0.15190 0.7444 10 134 29 0.21642 0.5833 11 105 25 0.23810 0.4444 12 80 26 0.32500 0.3000
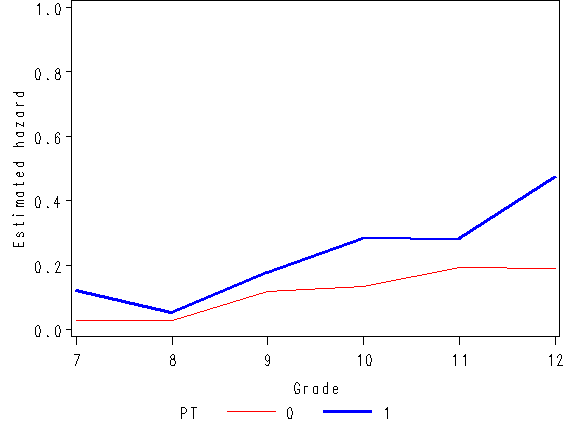
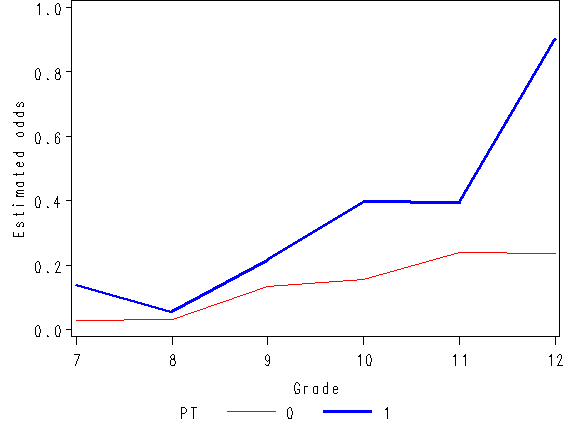
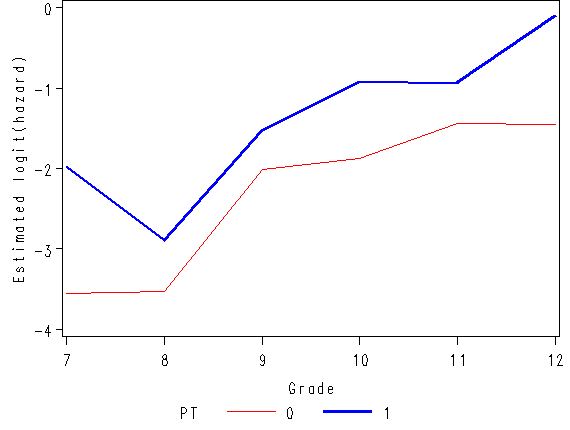
Figure 11.2, page 363
Manipulate the data set fig11_1b containing the hazard function created for Figure 11.1 in order to create the estimated odds and the estimated logit(hazard).
data fig11_2;
set fig11_1b;
odds = hazard/(1-hazard);
logith = log(odds);
run;
goptions reset=all ;
symbol1 c=red i=join;
symbol2 c=blue i=join width=2;
axis1 order=(0 to 1 by 0.2) minor = none label=(a=90 'Estimated hazard');
axis2 order=(0 to 1 by 0.2) minor = none label=(a=90 'Estimated odds');
axis3 order=(-4 to 0 by 1) minor = none label=(a=90 'Estimated logit(hazard)');
axis4 order =(7 to 12 by 1) minor = none label=('Grade');
proc gplot data=fig11_2;
format time 3.0;
plot hazard*time = pt / vaxis=axis1 haxis=axis4;
plot odds*time = pt / vaxis=axis2 haxis = axis4;
plot logith*time = pt / vaxis=axis3 haxis = axis4;
run;
quit;
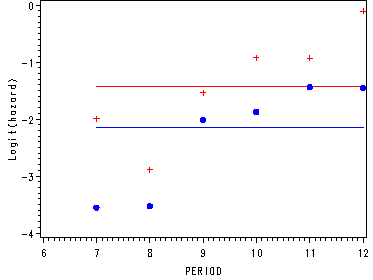
Figure 11.3, page 366
Producing the empirical logits–the dots and pluses in the graphs.
proc sort data=datasets.firstsex_pp out=sort; by period pt event; run; proc means data=sort1 noprint; by period pt; var id; output out=test n=c1; run; proc sort data=test; by period pt; run; data m1; merge first test; by period pt; run; proc means data=sort noprint; by period pt event; var id; output out=test1 n=c2; run; proc sort data=m1; by period pt event; run; proc sort data=test1; by period pt event; run; data m2; merge m1 test1; by period pt event; run; proc sort data=m2; by c1 c2; run; data small; set m2; by c1 c2; if first.c1 or first.c2; keep period pt event c1 c2; if event=1; run; data small; set small; prob = c2/c1 ; if pt=0 then pt0 = log(prob/(1-prob)); if pt=1 then pt1 = log(prob/(1-prob)); run; proc sort data=small out=period; by period; run;
Fitting the constant model and graphing the predicted model and the empirical logits.
ods listing close;
ods output parameterestimates=est_c;
proc logistic data=datasets.firstsex_pp descending;
model event= pt ;
run;
ods listing;
data _null_;
set est_c;
if variable='PT' then call symput('PT', estimate);
if variable='Intercept' then call symput('int', estimate);
run;
data constant;
set period;
c0 = &int ;
c1 = &int + &pt;
run;
goptions reset=all;
symbol1 c=blue i=j;
symbol2 c=red i=j;
symbol3 c=blue v=dot;
symbol4 c=red v=plus;
axis1 order=(-4 to 0 by 1) label=(a=90 'Logit(hazard)');
axis2 order=(6 to 12 by 1);
proc gplot data=constant;
plot (c0 c1 pt0 pt1)*period / overlay vaxis=axis1 haxis=axis2;
run;
quit;
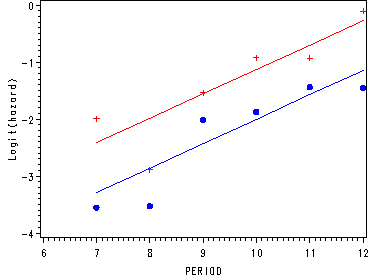
Fitting the linear model and graphing the predicted model and the empirical logits.
ods output parameterestimates=est_l;
ods listing close;
proc logistic data=datasets.firstsex_pp descending;
model event=period pt ;
run;
ods listing;
data _null_;
set est_l;
if variable='PT' then call symput('PT', estimate);
if variable='PERIOD' then call symput('per', estimate);
if variable='Intercept' then call symput('int', estimate);
run;
data linear;
set period;
lin0 = &int + &per*period;
lin1 = &int + &pt + &per*period;
run;
goptions reset=all;
symbol1 c=blue i=j;
symbol2 c=red i=j;
symbol3 c=blue v=dot;
symbol4 c=red v=plus;
axis1 order=(-4 to 0 by 1) label=(a=90 'Logit(hazard)');
axis2 order=(6 to 12 by 1);
proc gplot data=linear;
plot (lin0 lin1 pt0 pt1)*period / overlay vaxis=axis1 haxis=axis2;
run;
quit;
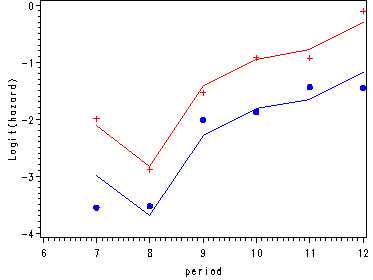
Fitting the non-linear model and graphing the predicted model and the empirical logits.
ods output parameterestimates=est;
ods listing close;
proc logistic data=datasets.firstsex_pp descending;
model event=D7-D12 pt / noint;
run;
ods listing;
*computing the logit(hazard) for pt=1 as well as the odds and hazard estimates ;
* for each level of pt.;
data _null_;
set est;
if variable='PT' then call symput('PT', estimate);
run;
data nlin;
set est;
keep estimate estimate1 period;
period = substr(variable, 2, 2) + 0;
estimate1 = estimate + &pt;
if variable = "PT" then delete;
run;
data nlingraph;
merge nlin period;
by period;
run;
goptions reset=all;
symbol1 c=blue i=j;
symbol2 c=red i=j;
symbol2 c=red i=j;
symbol3 c=blue v=dot;
axis1 order=(-4 to 0 by 1) label=(a=90 'Logit(hazard)');
axis2 order=(6 to 12 by 1);
proc gplot data=nlingraph;
format estimate 2.;
plot (estimate estimate1 pt0 pt1)*period / overlay vaxis=axis1 haxis=axis2;
run;
quit;
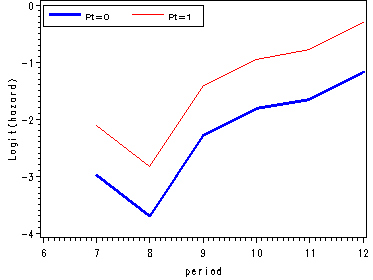
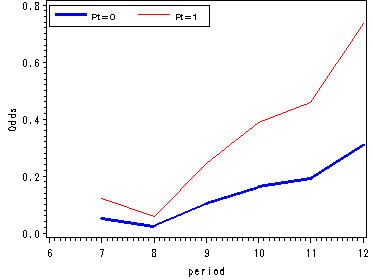
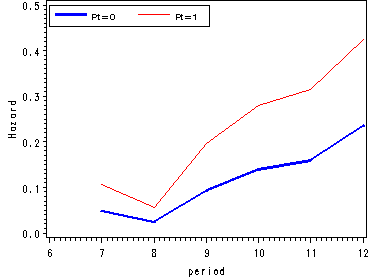
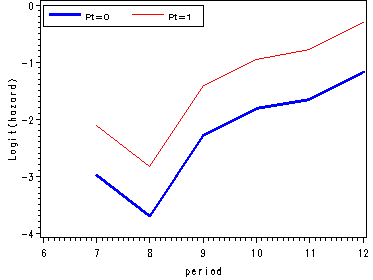
Figure 11.4, page 374
We fit a logit model to firstsex data using dummy variables for time and output the estimates from proc logistic in a data set called est. Since we are not focusing on the logistic output we have suppressed it using the ods listing close statement.
ods output parameterestimates=est; ods listing close; proc logistic data=datasets.firstsex_pp descending; model event=D7-D12 pt / noint; run; ods listing;
Using the macro variable syntax we save the value of the parameter estimate for pt in a macro variable called pt. In the next data step we are computing the logit(hazard) for pt=1 as well as the odds and hazard estimates for each level of pt.
data _null_;
set est;
if variable='PT' then call symput('PT', estimate);
run;
data fig3_4;
set est;
keep estimate estimate1 period hazard0 hazard1 odds0 odds1 beta;
period = substr(variable, 2, 2) + 0;
estimate1 = estimate + &pt;
if variable = "PT" then delete;
odds0 = exp(estimate);
odds1 = exp(estimate1);
hazard0 = odds0/(1+odds0);
hazard1 = odds1/(1+odds1);
beta = &pt;
run;
goptions reset=all;
symbol1 c=blue i=j width=2;
symbol2 c=red i=join;
axis1 order=(-4 to 0 by 1) label=(a=90 'Logit(hazard)');
axis2 order=(0 to 0.8 by 0.2) label=(a=90 'Odds');
axis3 order=(0 to 0.5 by 0.1) label=(a=90 'Hazard');
axis4 order=(6 to 12 by 1);
legend label=none value=(height=1 font=swiss 'Pt=0' 'Pt=1' )
position=(top left inside) mode=share cborder=black;
proc gplot data=fig3_4;
format estimate 2.;
plot (estimate estimate1)*period / overlay vaxis=axis1 haxis=axis4 legend=legend;
plot (odds0 odds1)*period / overlay vaxis=axis2 haxis=axis4 legend=legend;
plot (hazard0 hazard1)*period / overlay vaxis=axis3 haxis=axis4 legend=legend;
run;
quit;
Table 11.3, page 386
* Model A ; proc logistic data="c:\alda\firstsex_pp" descending ; model event = d7 d8 d9 d10 d11 d12 / noint ; run;
Model Fit Statistics
Without With
Criterion Covariates Covariates
AIC 1139.534 663.955
SC 1139.534 692.226
-2 Log L 1139.534 651.955
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 487.5786 6 <.0001
Score 421.4842 6 <.0001
Wald 277.1388 6 <.0001
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
D7 1 -2.3979 0.2697 79.0611 <.0001
D8 1 -3.1167 0.3862 65.1115 <.0001
D9 1 -1.7198 0.2217 60.2016 <.0001
D10 1 -1.2867 0.2098 37.6195 <.0001
D11 1 -1.1632 0.2291 25.7699 <.0001
D12 1 -0.7309 0.2387 9.3751 0.0022
* Model B ;
proc logistic data="c:\alda\firstsex_pp" descending ;
model event = d7 d8 d9 d10 d11 d12 pt / noint ;
pt: test pt;
run;
Model Fit Statistics
Without With
Criterion Covariates Covariates
AIC 1139.534 648.662
SC 1139.534 681.644
-2 Log L 1139.534 634.662
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 504.8722 7 <.0001
Score 429.6738 7 <.0001
Wald 271.0944 7 <.0001
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
D7 1 -2.9943 0.3175 88.9379 <.0001
D8 1 -3.7001 0.4206 77.4055 <.0001
D9 1 -2.2811 0.2724 70.1309 <.0001
D10 1 -1.8226 0.2585 49.7268 <.0001
D11 1 -1.6542 0.2691 37.7872 <.0001
D12 1 -1.1791 0.2716 18.8484 <.0001
PT 1 0.8736 0.2174 16.1471 <.0001
Linear Hypotheses Testing Results
Wald
Label Chi-Square DF Pr > ChiSq
pt 16.1471 1 <.0001
* Model C ; proc logistic data="c:\alda\firstsex_pp" descending ; model event = d7 d8 d9 d10 d11 d12 pas / noint ; pas: test pas; run;
Model Fit Statistics
Without With
Criterion Covariates Covariates
AIC 1139.534 651.169
SC 1139.534 684.151
-2 Log L 1139.534 637.169
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 502.3654 7 <.0001
Score 428.8665 7 <.0001
Wald 272.9013 7 <.0001
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
D7 1 -2.4646 0.2741 80.8416 <.0001
D8 1 -3.1591 0.3890 65.9498 <.0001
D9 1 -1.7297 0.2245 59.3638 <.0001
D10 1 -1.2851 0.2127 36.5178 <.0001
D11 1 -1.1360 0.2324 23.8998 <.0001
D12 1 -0.6421 0.2428 6.9921 0.0082
PAS 1 0.4428 0.1140 15.0984 0.0001
Linear Hypotheses Testing Results
Wald
Label Chi-Square DF Pr > ChiSq
pas 15.0984 1 0.0001
* Model D ; proc logistic data="c:\alda\firstsex_pp" descending ; model event = d7 d8 d9 d10 d11 d12 pt pas / noint ; pt: test pt; pas: test pas; run;
Model Fit Statistics
Without With
Criterion Covariates Covariates
AIC 1139.534 645.147
SC 1139.534 682.841
-2 Log L 1139.534 629.147
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 510.3870 8 <.0001
Score 432.4782 8 <.0001
Wald 269.8099 8 <.0001
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
D7 1 -2.8932 0.3206 81.4252 <.0001
D8 1 -3.5847 0.4231 71.7689 <.0001
D9 1 -2.1502 0.2775 60.0588 <.0001
D10 1 -1.6932 0.2647 40.9314 <.0001
D11 1 -1.5177 0.2757 30.2938 <.0001
D12 1 -1.0099 0.2811 12.9040 0.0003
PT 1 0.6605 0.2367 7.7855 0.0053
PAS 1 0.2964 0.1254 5.5872 0.0181
Linear Hypotheses Testing Results
Wald
Label Chi-Square DF Pr > ChiSq
pt 7.7855 1 0.0053
pas 5.5872 1 0.0181
Table 11.4, page 388
Interpreting the results of fitting an initial discrete-time hazard model including the main effect of time. Expressing parameter estimates as fitted odds and fitted hazard probabilities. Note that SAS, by default, will produce the parameter estimate and fitted odds without any extra effort. However, you can use the steps below to capture the output using ODS and then manipulate it to create the table below like Table 14.1 which includes the Fitted Hazard.
* Model A, repeated but capturing parameter estimates in file parest ; ods output ParameterEstimates=parest ; proc logistic data="c:\alda\firstsex_pp" descending ; model event = d7 d8 d9 d10 d11 d12 / noint ; run; ods output close;
<Output suppressed to save space>
* Computing odds and hazard;
data table11_4;
set parest;
FittedOdds = exp(Estimate);
Hazard = 1 / (1 + exp(-Estimate)) ;
run;
proc print data=table11_4;
var Variable Estimate FittedOdds Hazard ;
run;
Fitted
Obs Variable Estimate Odds Hazard
1 D7 -2.3979 0.09091 0.08333
2 D8 -3.1167 0.04430 0.04242
3 D9 -1.7198 0.17910 0.15190
4 D10 -1.2867 0.27619 0.21642
5 D11 -1.1632 0.31250 0.23810
6 D12 -0.7309 0.48148 0.32500
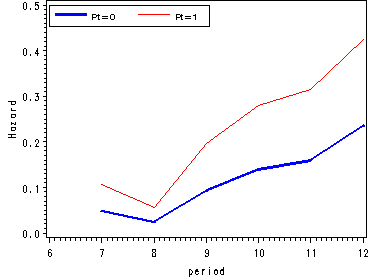
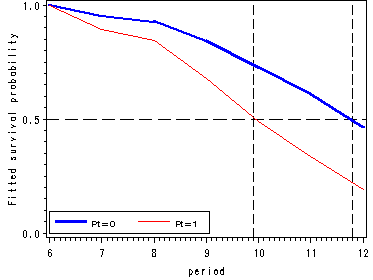
Figure 11.6, page 393
goptions reset=all;
symbol1 c=blue i=j width=2;
symbol2 c=red i=join;
axis1 order=(-4 to 0 by 1) label=(a=90 'Logit(hazard)');
axis2 order=(0 to 0.5 by 0.1) label=(a=90 'Hazard');
axis3 order=(0 to 1 by 0.5) label=(a=90 'Fitted survival probability');
axis4 order=(6 to 12 by 1);
legend1 label=none value=(height=1 font=swiss 'Pt=0' 'Pt=1' )
position=(top left inside) mode=share cborder=black;
legend2 label=none value=(height=1 font=swiss 'Pt=0' 'Pt=1' )
position=(bottom left inside) mode=share cborder=black;
proc gplot data=fig3_6;
format estimate 2.;
plot (estimate estimate1)*period / overlay vaxis=axis1 haxis=axis4 legend=legend1;
plot (odds0 odds1)*period / overlay vaxis=axis2 haxis=axis4 legend=legend1;
plot (survivor0 survivor1)*period / overlay vaxis=axis3 haxis=axis4 legend=legend2
vref=.5 lvref=21 href=9.9 11.8 lhref=21;
run;
quit;
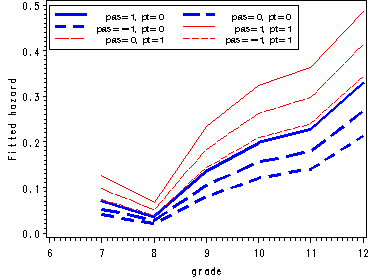
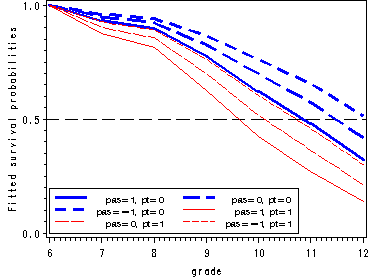
Figure 11.7, page 395
Presents the prototypical hazard and survivor functions for model D in Table 11.3.
Fitting the logistic model with main effects pt and pas and outputting the parameter estimates to the data set estimate.
proc logistic data=datasets.firstsex_pp descending out=estimate noprint; model event = d7-d12 PT PAS/noint; run;
Reconstructing fitted hazard and survivor functions.
data estimate (replace=yes);
set estimate;
array time[6] d7-d12;
do group = 0 to 1;
do antisocial = -1 to 1;
survivor = 1;
do period = 1 to 6;
grade = period + 6;
x = time[period] + group*PT +antisocial*PAS;
hazard = 1/(1 + exp(-x));
survivor = (1 - hazard)*survivor;
output;
end;
end;
end;
keep group antisocial grade x hazard survivor;
run;
Adding initial observations where grade=6 for each combination of pt and pas; generating a variable called ag for each combination of levels for pt and pas for graphing purposes and finally sorting the data.
data temp;
input survivor antisocial group grade;
cards;
1 1 0 6
1 0 0 6
1 -1 0 6
1 1 1 6
1 0 1 6
1 -1 1 6
;
run;
data estimate;
set temp estimate;
if antisocial=1 and group=0 then ag = 1;
if antisocial=0 and group=0 then ag = 2;
if antisocial=-1 and group=0 then ag = 3;
if antisocial=1 and group=1 then ag = 4;
if antisocial=0 and group=1 then ag = 5;
if antisocial=-1 and group=1 then ag = 6;
run;
proc sort data=estimate;
by group antisocial;
run;
goptions reset=all;
symbol1 c=blue i=j width=2;
symbol2 c=blue i=j width=2 l=4;
symbol3 c=blue i=j width=2 l=3;
symbol4 c=red i=j;
symbol5 c=red i=j l=4;
symbol6 c=red i=j l=3;
axis1 order=(0 to 0.5 by 0.1) label=(a=90 'Fitted hazard');
axis2 order=(0 0.5 1.0) label=(a=90 'Fitted survival probabilities');
legend1 label=none value=(height=1 font=swiss
'pas=1, pt=0' 'pas=0, pt=0' 'pas=-1, pt=0' 'pas=1, pt=1' 'pas=0, pt=1' 'pas=-1, pt=1')
position=(top left inside) mode=share cborder=black;
legend2 label=none value=(height=1 font=swiss
'pas=1, pt=0' 'pas=0, pt=0' 'pas=-1, pt=0' 'pas=1, pt=1' 'pas=0, pt=1' 'pas=-1, pt=1')
position=(bottom left inside) mode=share cborder=black;
proc gplot data=estimate;
plot hazard*grade=ag / overlay vaxis=axis1 legend=legend1;
plot survivor*grade=ag / overlay vaxis=axis2 legend=legend2 vref=0.5 lvref=21;
run;
quit;