Table 15.1, page 548
Including the effects of time-varying predictors in a Cox regression model.
Model A: Predictors include birthyr and the time-invariant predictors earlymj and earlyod.
proc phreg data='c:aldafirstcocaine';
model cokeage*censor(1)= birthyr earlymj earlyod/ties = efron;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 5525.059 5277.228
AIC 5525.059 5283.228
SBC 5525.059 5295.064
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
BIRTHYR 1 0.15508 0.01993 60.5637 <.0001 1.168
EARLYMJ 1 1.21707 0.16403 55.0532 <.0001 3.377
EARLYOD 1 0.79121 0.19620 16.2626 <.0001 2.206
Model B: Predictors include birthyr and the time-varying predictors usedmj and usedod.
proc phreg data='c:aldafirstcocaine';
model cokeage*censor(1)= birthyr usedmj usedod/ties = efron;
if mjyes = 1 and mjage < cokeage then usedmj = 1;
else usedmj = 0;
if odyes = 1 and odage < cokeage then usedod = 1;
else usedod = 0;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 5525.059 4669.096
AIC 5525.059 4675.096
SBC 5525.059 4686.932
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
BIRTHYR 1 0.10741 0.02145 25.0797 <.0001 1.113
usedmj 1 2.55177 0.28095 82.4918 <.0001 12.830
usedod 1 1.85386 0.12921 205.8483 <.0001 6.384
Model C: Includes predictor birthyr and the time-varying predictors usedmj, soldmj, usedod and moreod.
proc phreg data='c:aldafirstcocaine';
model cokeage*censor(1)= birthyr usedmj soldmj usedod moreod/ties = efron;
if mjyes = 1 and mjage < cokeage then usedmj = 1;
else usedmj = 0;
if sellmjyes = 1 and sellmjage < cokeage then soldmj = 1;
else soldmj = 0;
if odyes = 1 and odage < cokeage then usedod = 1;
else usedod = 0;
if sdyes = 1 and sdage < cokeage then moreod = 1;
else moreod = 0;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 5525.059 4580.537
AIC 5525.059 4590.537
SBC 5525.059 4610.264
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
BIRTHYR 1 0.08493 0.02183 15.1321 0.0001 1.089
usedmj 1 2.45920 0.28357 75.2073 <.0001 11.695
soldmj 1 0.68989 0.12263 31.6518 <.0001 1.993
usedod 1 1.25110 0.15656 63.8587 <.0001 3.494
moreod 1 0.76037 0.13066 33.8656 <.0001 2.139
Model D: Includes predictors birthyr and the time-invariant predictors earlymj and earlyod as well as the time-varying predictors usedmj, soldmj, usedod and moreod.
proc phreg data='c:aldafirstcocaine';
model cokeage*censor(1)= birthyr earlymj usedmj soldmj earlyod usedod moreod/ties = efron;
if mjyes = 1 and mjage < cokeage then usedmj = 1;
else usedmj = 0;
if sellmjyes = 1 and sellmjage < cokeage then soldmj = 1;
else soldmj = 0;
if odyes = 1 and odage < cokeage then usedod = 1;
else usedod = 0;
if sdyes = 1 and sdage < cokeage then moreod = 1;
else moreod = 0;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 5525.059 4580.311
AIC 5525.059 4594.311
SBC 5525.059 4621.929
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
BIRTHYR 1 0.08350 0.02257 13.6855 0.0002 1.087
EARLYMJ 1 0.07527 0.17090 0.1940 0.6596 1.078
usedmj 1 2.45222 0.28425 74.4230 <.0001 11.614
soldmj 1 0.67887 0.12496 29.5160 <.0001 1.972
EARLYOD 1 -0.08028 0.20325 0.1560 0.6929 0.923
usedod 1 1.25429 0.15723 63.6377 <.0001 3.505
moreod 1 0.76378 0.13219 33.3838 <.0001 2.146
Table 15.2, page 555
Comparing alternative imputation strategies for time-varying predictors.
Model A: Predictors include needle and basemood.
proc phreg data='c:aldarelapse_days';
model days*censor(1)= nasal basemood/ties = efron;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 528.186 515.680
AIC 528.186 519.680
SBC 528.186 523.935
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard Variable
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio Label
NASAL 1 1.02073 0.31407 10.5627 0.0012 2.775 NEEDLE
BASEMOOD 1 -0.00375 0.01471 0.0649 0.7989 0.996
Model B: Predictors include needle and weekmood (the value in the immediate prior week).
proc phreg data='c:aldarelapse_days';
model days*censor(1)=nasal weekmood /ties=efron;
array mood[12] weekmood1-weekmood12;
do i=1 to days;
if (int(days/7)+1)=i then weekmood=mood[i];
end;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 528.186 509.576
AIC 528.186 513.576
SBC 528.186 517.831
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard Variable
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio Label
NASAL 1 1.07958 0.31574 11.6912 0.0006 2.943 NEEDLE
weekmood 1 -0.03490 0.01387 6.3359 0.0118 0.966
Model C: Predictors include needle and daymood (a linearly interpolated estimates of the person's mood on the immediately prior day).
proc phreg data='c:aldarelapse_days';
model days*censor(1)=nasal intmood/ties=efron;
array avemood[13] avermood00-avermood12;
do i=1 to days;
thisweek = 1+int((i-1)/7);
thisday = i - ((thisweek-1)*7);
intmood=((8-thisday)/7)*avemood[thisweek]+((thisday-1)/7)*avemood[thisweek+1];
end;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 528.186 502.664
AIC 528.186 506.664
SBC 528.186 510.918
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard Variable
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio Label
NASAL 1 1.12075 0.31700 12.5000 0.0004 3.067 NEEDLE
intmood 1 -0.05438 0.01489 13.3307 0.0003 0.947
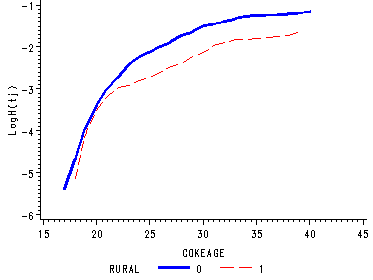
Figure 15.2, page 559
The graphs represent the sample functions of the log cumulative hazard functions for each level of rural.
proc phreg data='c:aldafirstcocaine' noprint; model cokeage*censor(1) = ; strata rural; baseline out=rural loglogs=logh ; run; goptions reset=all; symbol1 c=blue i=j line=1 width=2; symbol2 c=red i=j line=21; axis1 label=(a=90 'LogH(tj)'); axis2 order=(15 to 45 by 5); proc gplot data=rural; format cokeage 2.0; plot logh*cokeage = rural / vaxis=axis1 haxis=axis2 noframe; run; quit;
Table 15.3, page 560
Fitting a stratified Cox regression model
The unstratified model which corresponds to the first column of the table.
proc phreg data='c:aldafirstcocaine';
model cokeage*censor(1)= birthyr usedmj soldmj usedod moreod/ties = efron;
if mjyes = 1 and mjage < cokeage then usedmj = 1;
else usedmj = 0;
if sellmjyes = 1 and sellmjage < cokeage then soldmj = 1;
else soldmj = 0;
if odyes = 1 and odage < cokeage then usedod = 1;
else usedod = 0;
if sdyes = 1 and sdage < cokeage then moreod = 1;
else moreod = 0;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 5525.059 4580.537
AIC 5525.059 4590.537
SBC 5525.059 4610.264
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
BIRTHYR 1 0.08493 0.02183 15.1321 0.0001 1.089
usedmj 1 2.45920 0.28357 75.2073 <.0001 11.695
soldmj 1 0.68989 0.12263 31.6518 <.0001 1.993
usedod 1 1.25110 0.15656 63.8587 <.0001 3.494
moreod 1 0.76037 0.13066 33.8656 <.0001 2.139
The stratified model corresponding to the second column in the table.
proc phreg data='c:aldafirstcocaine';
model cokeage*censor(1)= birthyr usedmj soldmj usedod moreod/ties = efron;
strata rural;
if mjyes = 1 and mjage < cokeage then usedmj = 1;
else usedmj = 0;
if sellmjyes = 1 and sellmjage < cokeage then soldmj = 1;
else soldmj = 0;
if odyes = 1 and odage < cokeage then usedod = 1;
else usedod = 0;
if sdyes = 1 and sdage < cokeage then moreod = 1;
else moreod = 0;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 5200.202 4271.899
AIC 5200.202 4281.899
SBC 5200.202 4301.626
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
BIRTHYR 1 0.08537 0.02187 15.2318 <.0001 1.089
usedmj 1 2.45805 0.28371 75.0643 <.0001 11.682
soldmj 1 0.68486 0.12284 31.0826 <.0001 1.984
usedod 1 1.25185 0.15665 63.8600 <.0001 3.497
moreod 1 0.74679 0.13126 32.3691 <.0001 2.110
Fitting the model separately for each level of rural.
proc sort data='c:aldafirstcocaine' out=sorted;
by rural;
run;
proc phreg data=sorted;
model cokeage*censor(1)= birthyr usedmj soldmj usedod moreod/ties = efron;
by rural;
if mjyes = 1 and mjage < cokeage then usedmj = 1;
else usedmj = 0;
if sellmjyes = 1 and sellmjage < cokeage then soldmj = 1;
else soldmj = 0;
if odyes = 1 and odage < cokeage then usedod = 1;
else usedod = 0;
if sdyes = 1 and sdage < cokeage then moreod = 1;
else moreod = 0;
run;
<output omitted>
RURAL=0
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 4586.246 3809.358
AIC 4586.246 3819.358
SBC 4586.246 3838.323
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
BIRTHYR 1 0.08127 0.02358 11.8814 0.0006 1.085
usedmj 1 2.43696 0.31545 59.6804 <.0001 11.438
soldmj 1 0.71514 0.13127 29.6793 <.0001 2.044
usedod 1 1.27272 0.17157 55.0304 <.0001 3.571
moreod 1 0.69249 0.14102 24.1143 <.0001 1.999
RURAL=1
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 613.956 460.957
AIC 613.956 470.957
SBC 613.956 480.901
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
BIRTHYR 1 0.10977 0.05843 3.5296 0.0603 1.116
usedmj 1 2.51818 0.64874 15.0671 0.0001 12.406
soldmj 1 0.45410 0.35296 1.6552 0.1983 1.575
usedod 1 1.14528 0.38424 8.8840 0.0029 3.143
moreod 1 1.10510 0.35232 9.8383 0.0017 3.020
Table 15.4, page 566
Fitting a non-proportional hazards Cox regression model.
Model A: Predictors include the main effect of treat.
proc phreg data='c:aldalengthofstay';
model days*censor(1)=treat/ties=efron;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 1437.520 1436.628
AIC 1437.520 1438.628
SBC 1437.520 1441.775
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
TREAT 1 0.14570 0.15415 0.8934 0.3446 1.157
Model B: The effects of treat varies linearly over time.
proc phreg data='c:aldalengthofstay';
model days*censor(1)=treat treattime/ties=efron;
treattime=treat*(days-1);
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 1437.520 1431.374
AIC 1437.520 1435.374
SBC 1437.520 1441.669
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
TREAT 1 0.70613 0.29240 5.8321 0.0157 2.026
treattime 1 -0.02082 0.00921 5.1143 0.0237 0.979
Model C: The effects of treat differ week by week.
proc phreg data='c:aldalengthofstay';
model days*censor(1)=treat1-treat6/ties=efron;
array dummy[5] treat1-treat5;
do i=1 to 5;
if ceil(days/7) = i then dummy[i]=treat;
else dummy[i]=0;
end;
if days >= 35 then treat6=treat; else treat6=0;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 1437.520 1417.730
AIC 1437.520 1429.730
SBC 1437.520 1448.615
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
treat1 1 1.57109 0.64060 6.0149 0.0142 4.812
treat2 1 0.56779 0.49285 1.3272 0.2493 1.764
treat3 1 0.84970 0.36207 5.5075 0.0189 2.339
treat4 1 -0.34986 0.36415 0.9231 0.3367 0.705
treat5 1 -0.76597 0.41608 3.3890 0.0656 0.465
treat6 1 -0.09929 0.31105 0.1019 0.7496 0.905
Model D: The effect of treat varies linearly with the logarithm (to base 2) of time.
proc phreg data='c:aldalengthofstay';
model days*censor(1)=treat treatlt/ties=efron;
treatlt=treat*log2(days);
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 1437.520 1423.062
AIC 1437.520 1427.062
SBC 1437.520 1433.357
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
TREAT 1 2.53337 0.76031 11.1023 0.0009 12.596
treatlt 1 -0.53009 0.16188 10.7230 0.0011 0.589
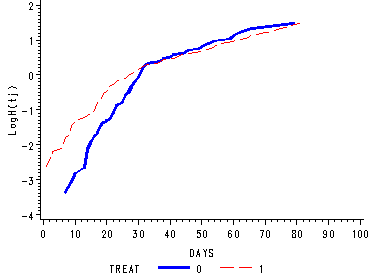
Figure 15.3, page 567
Figure 15.3--top panel
Depicts the log cumulative hazard functions for each level of treat when there is an interaction with time.
proc phreg data='c:aldalengthofstay' noprint; model days*censor(1)= /ties=efron; strata treat; baseline out=treat loglogs=logh; run; goptions reset=all; symbol1 c=blue i=j line=1 width=2; symbol2 c=red i=j line=21; axis1 label=(a=90 'LogH(tj)'); proc gplot data=treat; plot logh*days=treat /vaxis=axis1 noframe ; run; quit;
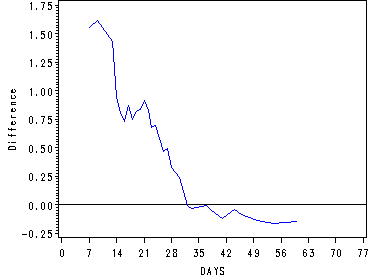
Figure 15.3--bottom panel
The difference in sample log cumulative hazard functions for each level of treat.
data treat0 (where=(treat=0) rename=(logh=logh0))
treat1 (where=(treat=1) rename=(logh=logh1));
set treat;
run;
data graph;
merge treat0 treat1;
by days;
difflogh=logh1-logh0;
drop treat;
run;
goptions reset=all;
symbol1 c=blue i=j;
axis1 label=(a=90 'Difference') order=(-0.25 to 1.75 by 0.25);
axis2 order=(0 to 77 by 7);
proc gplot data=graph;
plot difflogh*days /vaxis=axis1 haxis=axis2 vref=0;
run;
quit;
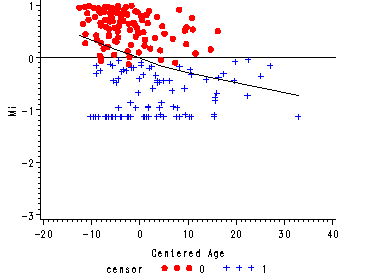
Figure 15.4, page 573
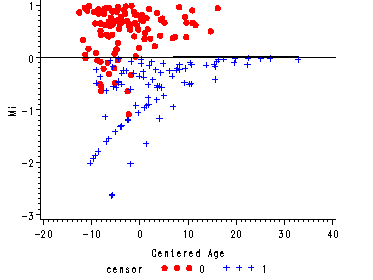
Figure 15.4--top panel
The martingale residual versus the predictor age from the null model with a lowess curve overlaid.
** Computing the martingale residuals for the Null Model **;
proc phreg data='c:aldarearrest' noprint;
model months*censor(1)= /ties=efron;
id id;
output out=nullres resmart=nullmart /method=pl;
run;
proc sort data=nullres;
by id;
run;
data combo_null;
merge 'c:aldarearrest' nullres;
drop personal property;
run;
ods output OutputStatistics=nullsm;
ods listing close;
proc loess data=combo_null;
model nullmart=cage;
id id;
run;
ods listing;
data nullsm;
set nullsm;
Nsmooth = pred;
keep id Nsmooth;
run;
proc sort data=nullsm;
by id;
run;
data graph_null;
merge nullsm combo_null;
by id;
run;
proc sort data=graph_null;
by cage;
run;
goptions reset=all;
axis1 order=(-3 to 1 by 1) label=(a=90 'Mi');
axis2 order=(-20 to 40 by 10) label=('Centered Age');
symbol1 color=red value=dot i=none;
symbol2 color=blue value=plus i=none;
symbol3 color=black value=none i=join;
proc gplot data=graph_null;
plot1 nullmart*cage=censor/haxis=axis2 vaxis=axis1 vref=0 noframe;
plot2 Nsmooth *cage=3 / haxis=axis2 vaxis=axis1 noaxis;
run;
quit;
Figure 15.4--bottom panel
The martingale residual versus age for a model that includes age, personal and property (model D of Table 15.1)
proc phreg data='c:aldarearrest' noprint;
model months*censor(1)=cage personal property/ties=efron;
id id;
output out=Dres resdev=Ddev resmart=Dmart/method=pl;
run;
proc sort data=Dres;
by id;
run;
data comboD;
merge 'c:aldarearrest' Dres;
drop personal property;
run;
ods output OutputStatistics=Dsm;
ods listing close;
proc loess data=comboD;
model Dmart=cage;
id id;
run;
ods listing;
data Dsm;
set Dsm;
Dsmooth = pred;
keep id Dsmooth;
run;
proc sort data=Dsm;
by id;
run;
data graphD;
merge Dsm comboD;
by id;
run;
proc sort data=graphD;
by cage;
run;
goptions reset=all;
axis1 order=(-3 to 1 by 1) label=(a=90 'Mi');
axis2 order=(-20 to 40 by 10) label=('Centered Age');
symbol1 color=red value=dot i=none;
symbol2 color=blue value=plus i=none;
symbol3 color=black value=none i=join;
proc gplot data=graphD;
plot1 Dmart*cage=censor/ haxis=axis2 vaxis=axis1 vref=0 noframe;
plot2 Dsmooth*cage=3 / haxis=axis2 vaxis=axis1 noaxis;
run;
quit;
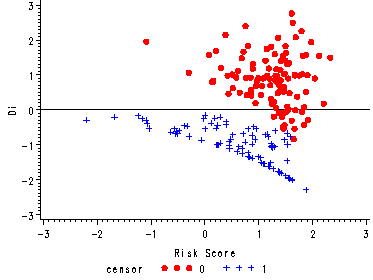
Figure 15.5, page 576
Stem-and-leaf plot, boxplot and scatter plot of the deviance residuals. In the scatter plot the residuals are plotted versus the risk score.
proc phreg data='c:aldarearrest' noprint;
model months*censor(1)=cage personal property/ties=efron;
id id;
output out=Dres resdev=Ddev resmart=Dmart xbeta=risk/method=pl;
run;
proc univariate data=Dres plot;
var Ddev;
run;
<output omitted>
Stem Leaf # Boxplot
26 7 1 |
24 00 2 |
22 6 1 |
20 785 3 |
18 23356 5 |
16 04795 5 |
14 1228055578 10 |
12 0115 4 |
10 022335725789 12 |
8 1135690001233889999 19 +-----+
6 2588919 7 | |
4 123678802337 12 | |
2 0318 4 | |
0 268978 6 | + |
-0 97597551 8 *-----*
-2 850099554110 12 | |
-4 444443332877644210 18 | |
-6 876321098874400 15 | |
-8 99852176443 11 +-----+
-10 208776542110 12 |
-12 87654741 8 |
-14 54216 5 |
-16 969221 6 |
-18 6491 4 |
-20 21 2 |
-22 09 2 |
----+----+----+----+
Multiply Stem.Leaf by 10**-1
goptions reset=all;
axis1 order=(-3 to 3 by 1) label=(a=90 'Di');
axis2 label=('Risk Score');
symbol1 color=red value=dot;
symbol2 color=blue value=plus;
proc gplot data=one;
plot Ddev*risk=censor/ haxis=axis2 vaxis=axis1 vref=0 noframe;
run;
quit;
Figure 15.6, page 580
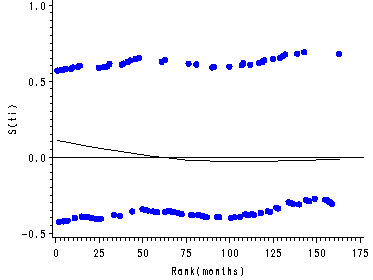
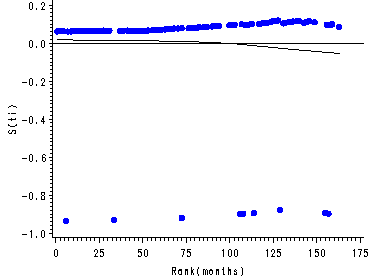
The Schoenfeld residuals from Model D versus ranked event time for the predictors personal, property and age. Each graph includes a lowess curve.
proc rank data='c:aldarearrest' out=one;
var months;
ranks ranktime;
run;
proc phreg data='c:aldarearrest' noprint;
model months*censor(1)=cage property personal/ties=efron;
id id;
output out=fitres ressch=schage schprop schpers /method=pl;
run;
proc sort data=fitres;
by id;
run;
data combo;
merge one fitres;
by id;
if censor = 0; *only keeping observed observations*;
run;
*Lowess smoothing for AGE *;
ods output OutputStatistics=agesm;
ods listing close;
proc loess data=combo;
model schage=ranktime;
id id;
run;
ods listing;
data agesm;
set agesm;
lowage = pred;
keep id lowage;
run;
proc sort data=agesm;
by id;
run;
* Lowess smoothing for PROPERTY *;
ods output OutputStatistics=propsm;
ods listing close;
proc loess data=combo;
model schprop=ranktime;
id id;
run;
ods listing;
data propsm;
set propsm;
lowprop = pred;
keep id lowprop;
run;
proc sort data=propsm;
by id;
run;
* Lowess smoothing for PERSON *;
ods output OutputStatistics=perssm;
ods listing close;
proc loess data=combo;
model schpers=ranktime;
id id;
run;
ods listing;
data perssm;
set perssm;
lowpers = pred;
keep id lowpers;
run;
proc sort data=perssm;
by id;
run;
* Merging the Schoenfeld residuals and lowess smooths together *;
data all;
merge combo agesm propsm perssm;
by id;
run;
proc corr data=all;
with schpers schprop schage;
var months ranktime;
run;
<output omitted>
Pearson Correlation Coefficients, N = 106
Prob > |r| under H0: Rho=0
months ranktime
schpers -0.07564 -0.08711
Schoenfeld Residual for personal 0.4409 0.3746
schprop -0.09639 -0.06769
Schoenfeld Residual for property 0.3256 0.4906
schage 0.25906 0.28199
Schoenfeld Residual for cage 0.0073 0.0034
proc sort data=all;
by ranktime;
run;
goptions reset=all;
symbol1 color=blue value=dot;
symbol2 i=join;
axis1 label=('Rank(months)') order=(0 to 175 by 25);
axis2 label=(a=90 'S(ti)') order=(-0.5 to 1.0 by 0.5);
axis3 label=(a=90 'S(ti)') order=(-1 to 0.20 by 0.2);
axis4 label=(a=90 'S(ti)') order=(-10 to 20.0 by 10);
proc gplot data=all;
plot (schpers lowpers)*ranktime/ overlay haxis=axis1 vaxis=axis2 noframe;
plot (schprop lowprop)*ranktime/ overlay haxis=axis1 vaxis=axis3 noframe;
plot (schage lowage)*ranktime/ overlay haxis=axis1 vaxis=axis4 noframe;
run;
quit;
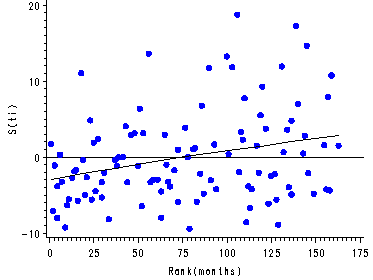
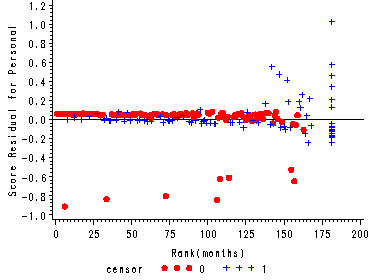
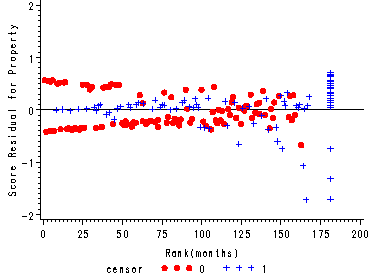
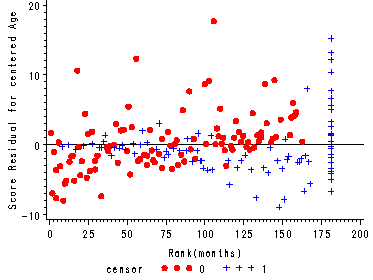
Figure 15.7, page 583
The score residuals versus the ranked event times for each predictor in the three predictor model which includes personal, property and age.
*using the same rank data from fig. 7.6;
proc phreg data='c:aldarearrest' noprint;
model months*censor(1)=cage personal property/ties=efron;
id id;
output out=scores ressco=scoage scoprop scopers/method=pl;
run;
proc sort data=scores;
by id;
run;
data combo;
merge one scores;
by id;
run;
goptions reset=all;
symbol1 color=red value=dot;
symbol2 color=blue value=plus;
axis1 label=('Rank(months)') order=(0 to 200 by 25);
axis2 label=(a=90 'Score Residual for Personal') order=(-1 to 1.2 by 0.2);
axis3 label=(a=90 'Score Residual for Property') order=(-2 to 2 by 1);
axis4 label=(a=90 'Score Residual for centered Age') order=(-10 to 20.0 by 10);
proc gplot data=combo;
plot scopers*ranktime=censor/ vref=0 haxis=axis1 vaxis=axis2 noframe;
plot scoprop*ranktime=censor/ vref=0 haxis=axis1 vaxis=axis3 noframe;
plot scoage*ranktime=censor/ vref=0 haxis=axis1 vaxis=axis4 noframe;
run;
quit;
Table 15.6, page 587
Illustrates the structure of the Supreme Court data set by displaying the data for three individual judges.
data judges; set 'c:aldajudges'; yearleft = .; if leave=1 then yearleft = year + tenure; left = 0; if dead = 1 then left = 1; if retire = 1 then left = 2; run; proc format; value left 0='censored' 1='dead' 2='retired'; run; proc print data=judges noobs; format left left.; where id=2 or id=13 or id=107; var id year yearleft left tenure dead retire leave; run; id year yearleft left tenure dead retire leave 2 1789 1795 retired 6 0 1 1 13 1801 1835 dead 34 1 0 1 107 1991 . censored 8 0 0 0
Table 15.7, page 592
Competing-risk survival analysis.
Model A: Fitting the model for the event of death only.
proc phreg data=judges;
model tenure*left(0 2) = age year / ties=efron;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 351.053 331.447
AIC 351.053 335.447
SBC 351.053 339.147
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
age 1 0.06711 0.02386 7.9096 0.0049 1.069
year 1 -0.01160 0.00289 16.0675 <.0001 0.988
Model B: Fitting the model for the event of retirement only.
proc phreg data=judges;
model tenure*left(0 1) = age year / ties=efron;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 395.406 373.497
AIC 395.406 377.497
SBC 395.406 381.437
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
age 1 0.10611 0.02579 16.9329 <.0001 1.112
year 1 0.0007141 0.00264 0.0730 0.7870 1.001
Model C: Fitting the model for the combined events of death or retirement.
proc phreg data=judges;
model tenure*left(0) = age year / ties=efron;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 739.620 711.765
AIC 739.620 715.765
SBC 739.620 720.975
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
age 1 0.08606 0.01766 23.7585 <.0001 1.090
year 1 -0.00522 0.00188 7.7118 0.0055 0.995
Table 15.8, page 601
Accounting for late entry into the risk set.
Model A: Appropriately including the late entrants.
proc phreg data='c:aldadoctors';
model exit*censor(1)= parttime age yrage / entry=entry ties=efron;
yrage = exit*age;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 4264.335 4214.515
AIC 4264.335 4220.515
SBC 4264.335 4232.459
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard Variable
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio Label
parttime 1 -1.34730 0.27638 23.7641 <.0001 0.260
age 1 0.04781 0.02421 3.8999 0.0483 1.049 Age at start
yrage 1 -0.02867 0.00906 10.0130 0.0016 0.972
Model B: Fitting the model only to those physicians hired during the measurement window.
proc phreg data='c:aldadoctors';
where entry=0;
model exit*censor(1)= parttime age yrage / ties=efron;
yrage = exit*age;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 560.760 558.391
AIC 560.760 564.391
SBC 560.760 570.521
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard Variable
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio Label
parttime 1 -0.17055 0.52080 0.1072 0.7433 0.843
age 1 0.03981 0.04553 0.7647 0.3819 1.041 Age at start
yrage 1 -0.00388 0.04458 0.0076 0.9306 0.996
Model C: Ignoring the presence of late entrants--shown for pedagogical purposes only since it an INCORRECT MODEL.
proc phreg data='c:aldadoctors';
model exit*censor(1)= parttime age yrage / ties=efron;
yrage = exit*age;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 4539.431 4482.988
AIC 4539.431 4488.988
SBC 4539.431 4500.932
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard Variable
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio Label
parttime 1 -1.33938 0.27649 23.4671 <.0001 0.262
age 1 0.09768 0.01918 25.9326 <.0001 1.103 Age at start
yrage 1 -0.03705 0.00779 22.6284 <.0001 0.964
Table 15.9, page 604
Empirically comparing alternative metrics for clocking time in Cox regression analysis.
Model A: Clocks time using session number.
proc phreg data='c:aldamonkeys';
model sessions*censor(1) = female bodywt initial_age / ties=efron;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 944.449 919.898
AIC 944.449 925.898
SBC 944.449 934.310
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
FEMALE 1 0.37197 0.19024 3.8229 0.0506 1.451
BODYWT 1 0.11632 0.02804 17.2124 <.0001 1.123
INITIAL_AGE 1 0.10636 0.03386 9.8698 0.0017 1.112
Model B: Clocks time using age but not accounting for late entry into the risk set.
proc phreg data='c:aldamonkeys';
model end_age*censor(1) = female bodywt initial_age / ties=efron;
run;
<output omitted>
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 944.449 915.073
AIC 944.449 921.073
SBC 944.449 929.485
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
FEMALE 1 0.29077 0.18876 2.3727 0.1235 1.337
BODYWT 1 0.10209 0.02770 13.5841 0.0002 1.107
INITIAL_AGE 1 -0.09391 0.03014 9.7064 0.0018 0.910
Model C: Clocks time using age and appropriately accounts for late entry.
proc phreg data='c:aldamonkeys';
model end_age*censor(1) = female bodywt initial_age / ties=efron entry=initial_age;
run;
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 914.654 896.822
AIC 914.654 902.822
SBC 914.654 911.234
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
FEMALE 1 0.31176 0.18785 2.7543 0.0970 1.366
BODYWT 1 0.10255 0.02771 13.6994 0.0002 1.108
INITIAL_AGE 1 -0.01891 0.03493 0.2931 0.5883 0.981