Note: This page has been updated for SAS 9.3 and is based on SAS 9.2 code provided by Raymond R. Balise of Stanford University. We thank Raymond R. Balise for sharing his SAS 9.2 code with us.
Figure 4.1, page 77
title "Figure 4.1 'Identifying a suitable functional form'";
proc sgpanel data = alcohol1_pp (where = (id in (4, 14, 23, 32, 41, 56, 65, 82)))
noautolegend ;
panelby id / columns = 4 rows = 2;
colaxis values = (13, 14, 15, 16, 17) ;
rowaxis min = 0 max = 4;
reg x = age y = alcuse;
run;
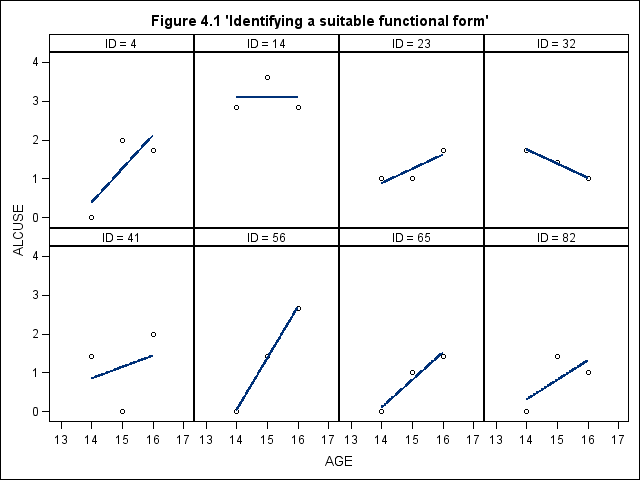
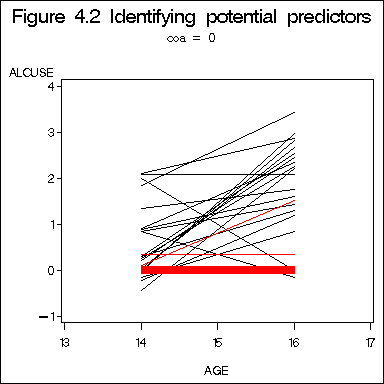
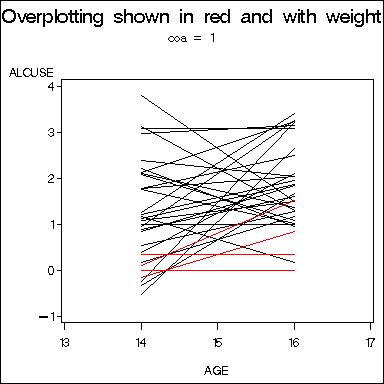
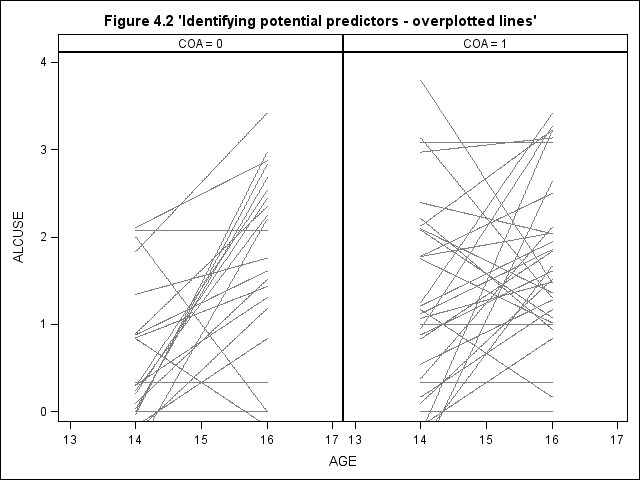
Figure 4.2, page 79. We will first present a simple-minded approach: no sub-sampling and no thickening the lines for coincident trajectories. The very much more complicated approach for sampling and adjusting the thickness of lines based on the number of coincidence of trajectories is presented afterwards.
title "Figure 4.2 'Identifying potential predictors - overplotted lines'"; proc sgpanel data = alcohol1_pp noautolegend ; panelby coa / columns = 2 rows = 1; colaxis values = (13 14, 15, 16, 17) ; rowaxis min = 0 max = 4 ; reg x = age y = alcuse / group = id nomarkers LINEATTRS = (COLOR= gray PATTERN = 1 THICKNESS = 1); run;
proc sql; select mean(peer) into :mpeer from alcohol1_pp; quit; proc format; value peer low -< &mpeer = "Low PEER" &mpeer - high = "High PEER"; run; title "Figure 4.2 'Identifying potential predictors - overplotted lines'"; proc sgpanel data = alcohol1_pp noautolegend; panelby peer / columns = 2 rows = 1 spacing = 5 novarname; format peer peer.; colaxis values = (13, 14, 15, 16, 17) ; rowaxis min = 0 max = 4 ; reg x = age y = alcuse / group = id nomarkers LINEATTRS = (COLOR= gray PATTERN = 1 THICKNESS = 1); run;
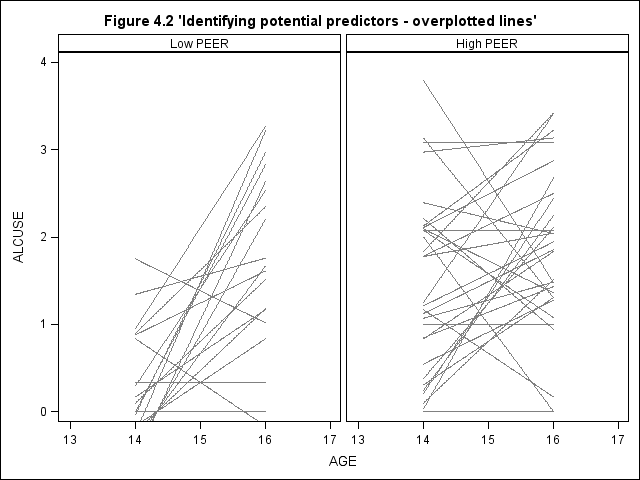
Now let us try to incorporate the idea of adjusting the thickness of the lines based on the number of coincidence of trajectories.
proc sort data = alcohol1_pp;
by id coa;
run;
proc reg data = alcohol1_pp outest = parameters noprint;
model alcuse = age_14;
by id coa;
run;
proc sql;
create table counts as
select coa, intercept as b_int, age_14 as b_age, count(id) as weight
from parameters
group by coa, intercept, age_14
order by weight;
quit;
data coa0 coa1 ;
set counts;
length function color $8;
retain xsys ysys hsys '2';
count = _N_;
function = "move";
size = weight/10;
if weight > 1 then color = "red";
else color = "black";
x = 14; y = b_int;
if coa = 0 then output coa0;
else output coa1;
function = "draw";
x = 16; y = b_int + 2 * b_age;
if coa = 0 then output coa0;
else output coa1;
run;
goptions reset = all ftext = swiss htitle = 5 htext = 3 gunit = pct
border cback = white hsize = 4in vsize = 4in;
filename outgraph 'c:\temp\mygraph1.gif';
goptions gsfname = outgraph dev = gif570;
axis1 order = (13 to 17 by 1) minor = none label=("AGE");
axis2 order = (-1 to 4 by 1) minor = none label=("ALCUSE");
symbol1 v= none;
title "Figure 4.2 Identifying potential predictors";
title2 "coa = 0";
proc gplot data = coa0 (where = (coa = 0));
plot y * x / anno = coa0 haxis = axis1 vaxis=axis2;
run;
quit;
filename outgraph 'c:temphttps://stats.idre.ucla.edu/wp-content/uploads/2016/02/mygraph2.gif';
goptions gsfname = outgraph dev = gif570;
title "Overplotting shown in red and with weight";
title2 "coa = 1";
proc gplot data = coa1 (where = (coa = 1));
plot y * x / anno = coa1 haxis = axis1 vaxis=axis2;
run;
quit;
Table 4.1, pages 94-95
* Table 4.1 ;
title1 "Table 4.1: Alcohol use data (alcohol1_pp): Fitted multilevel models for change";
proc mixed data="c:\alda\alcohol1_pp" method=ml noclprint noinfo covtest;
title2 "Model A";
class id;
model alcuse = /solution notest;
random intercept/sub=id;
proc mixed data="c:\alda\alcohol1_pp" method=ml noclprint noinfo covtest;
title2 "Model B";
class id;
model alcuse = age_14/solution notest;
random intercept age_14/type=un sub=id;
proc mixed data="c:\alda\alcohol1_pp" method=ml noclprint noinfo covtest;
title2 "Model C";
class id;
model alcuse = coa age_14 coa*age_14/solution notest;
random intercept age_14/type=un sub=id;
proc mixed data="c:\alda\alcohol1_pp" method=ml noclprint noinfo covtest;
title2 "Model D";
class id;
model alcuse = coa peer age_14 coa*age_14 peer*age_14 /solution notest;
random intercept age_14/type=un sub=id;
proc mixed data="c:\alda\alcohol1_pp" method=ml noclprint noinfo covtest;
title2 "Model E";
class id;
model alcuse = coa peer age_14 peer*age_14 /solution notest;
random intercept age_14/type=un sub=id;
proc mixed data="c:\alda\alcohol1_pp" method=ml noclprint noinfo covtest;
title2 "Model F";
class id;
model alcuse = coa cpeer age_14 cpeer*age_14 /solution notest;
random intercept age_14/type=un sub=id;
proc mixed data="c:\alda\alcohol1_pp" method=ml noclprint noinfo covtest;
title2 "Model G";
class id;
model alcuse = ccoa cpeer age_14 cpeer*age_14 /solution notest;
random intercept age_14/type=un sub=id;
run;
Table 4.1: Alcohol use data (alcohol1_pp): Fitted multilevel models for change
Model A
Covariance Parameter Estimates
Standard Z
Cov Parm Subject Estimate Error Value Pr Z
Intercept ID 0.5639 0.1191 4.73 <.0001
Residual 0.5617 0.06203 9.06 <.0001
Fit Statistics
-2 Log Likelihood 670.2
AIC (smaller is better) 676.2
AICC (smaller is better) 676.3
BIC (smaller is better) 683.4
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 0.9220 0.09571 81 9.63 <.0001
Table 4.1: Alcohol use data (alcohol1_pp): Fitted multilevel models for change
Model B
Covariance Parameter Estimates
Standard Z
Cov Parm Subject Estimate Error Value Pr Z
UN(1,1) ID 0.6244 0.1481 4.22 <.0001
UN(2,1) ID -0.06844 0.07008 -0.98 0.3288
UN(2,2) ID 0.1512 0.05647 2.68 0.0037
Residual 0.3373 0.05268 6.40 <.0001
Fit Statistics
-2 Log Likelihood 636.6
AIC (smaller is better) 648.6
AICC (smaller is better) 649.0
BIC (smaller is better) 663.1
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 79.70 <.0001
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 0.6513 0.1051 81 6.20 <.0001
AGE_14 0.2707 0.06245 81 4.33 <.0001
Table 4.1: Alcohol use data (alcohol1_pp): Fitted multilevel models for change
Model C
Covariance Parameter Estimates
Standard Z
Cov Parm Subject Estimate Error Value Pr Z
UN(1,1) ID 0.4876 0.1278 3.81 <.0001
UN(2,1) ID -0.05934 0.06573 -0.90 0.3666
UN(2,2) ID 0.1506 0.05639 2.67 0.0038
Residual 0.3373 0.05268 6.40 <.0001
Fit Statistics
-2 Log Likelihood 621.2
AIC (smaller is better) 637.2
AICC (smaller is better) 637.8
BIC (smaller is better) 656.5
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 66.15 <.0001
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 0.3160 0.1307 80 2.42 0.0179
COA 0.7432 0.1946 82 3.82 0.0003
AGE_14 0.2930 0.08423 80 3.48 0.0008
COA*AGE_14 -0.04943 0.1254 82 -0.39 0.6944
Table 4.1: Alcohol use data (alcohol1_pp): Fitted multilevel models for change
Model D
Covariance Parameter Estimates
Standard Z
Cov Parm Subject Estimate Error Value Pr Z
UN(1,1) ID 0.2409 0.09259 2.60 0.0046
UN(2,1) ID -0.00612 0.05500 -0.11 0.9115
UN(2,2) ID 0.1391 0.05481 2.54 0.0056
Residual 0.3373 0.05268 6.40 <.0001
Fit Statistics
-2 Log Likelihood 588.7
AIC (smaller is better) 608.7
AICC (smaller is better) 609.6
BIC (smaller is better) 632.8
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 53.86 <.0001
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept -0.3165 0.1481 79 -2.14 0.0356
COA 0.5792 0.1625 82 3.56 0.0006
PEER 0.6943 0.1115 82 6.23 <.0001
AGE_14 0.4294 0.1137 79 3.78 0.0003
COA*AGE_14 -0.01403 0.1248 82 -0.11 0.9107
PEER*AGE_14 -0.1498 0.08564 82 -1.75 0.0840
Table 4.1: Alcohol use data (alcohol1_pp): Fitted multilevel models for change
Model E
Covariance Parameter Estimates
Standard Z
Cov Parm Subject Estimate Error Value Pr Z
UN(1,1) ID 0.2409 0.09259 2.60 0.0046
UN(2,1) ID -0.00614 0.05501 -0.11 0.9111
UN(2,2) ID 0.1392 0.05481 2.54 0.0056
Residual 0.3373 0.05268 6.40 <.0001
Fit Statistics
-2 Log Likelihood 588.7
AIC (smaller is better) 606.7
AICC (smaller is better) 607.5
BIC (smaller is better) 628.4
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 53.86 <.0001
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept -0.3138 0.1461 79 -2.15 0.0348
COA 0.5712 0.1462 82 3.91 0.0002
PEER 0.6952 0.1113 82 6.25 <.0001
AGE_14 0.4247 0.1056 80 4.02 0.0001
PEER*AGE_14 -0.1514 0.08451 82 -1.79 0.0770
Table 4.1: Alcohol use data (alcohol1_pp): Fitted multilevel models for change
Model F
Covariance Parameter Estimates
Standard Z
Cov Parm Subject Estimate Error Value Pr Z
UN(1,1) ID 0.2409 0.09259 2.60 0.0046
UN(2,1) ID -0.00614 0.05501 -0.11 0.9111
UN(2,2) ID 0.1392 0.05481 2.54 0.0056
Residual 0.3373 0.05268 6.40 <.0001
Fit Statistics
-2 Log Likelihood 588.7
AIC (smaller is better) 606.7
AICC (smaller is better) 607.5
BIC (smaller is better) 628.4
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 53.86 <.0001
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 0.3939 0.1035 79 3.80 0.0003
COA 0.5712 0.1462 82 3.91 0.0002
CPEER 0.6952 0.1113 82 6.25 <.0001
AGE_14 0.2706 0.06127 80 4.42 <.0001
CPEER*AGE_14 -0.1514 0.08451 82 -1.79 0.0770
Table 4.1: Alcohol use data (alcohol1_pp): Fitted multilevel models for change
Model G
Covariance Parameter Estimates
Standard Z
Cov Parm Subject Estimate Error Value Pr Z
UN(1,1) ID 0.2409 0.09259 2.60 0.0046
UN(2,1) ID -0.00614 0.05501 -0.11 0.9111
UN(2,2) ID 0.1392 0.05481 2.54 0.0056
Residual 0.3373 0.05268 6.40 <.0001
Fit Statistics
-2 Log Likelihood 588.7
AIC (smaller is better) 606.7
AICC (smaller is better) 607.5
BIC (smaller is better) 628.4
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 53.86 <.0001
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 0.6515 0.07979 79 8.17 <.0001
CCOA 0.5712 0.1462 82 3.91 0.0002
CPEER 0.6952 0.1113 82 6.25 <.0001
AGE_14 0.2706 0.06127 80 4.42 <.0001
CPEER*AGE_14 -0.1514 0.08451 82 -1.79 0.0770
Table 4.1 (part 2), producing the output for pseudo R-squares which are described in Section 4.4.3 (page 102-104). We only show the code for Model D and the code can be applied for other models in this table.
1. An overall summary of total outcome variability explained
proc mixed data=alcohol1_pp method=ml ; title2 "Model D"; class id; model alcuse = coa peer age_14 coa*age_14 peer*age_14 /outpm=modeld; random intercept age_14/type=un sub=id; run; ods select fitstatistics; proc reg data = modeld; model alcuse = pred; run; quit;Root MSE 0.89686 R-Square 0.2912 Dependent Mean 0.92195 Adj R-Sq 0.2883 Coeff Var 97.278202. Pseudo R-squares computed from the variance components
*unconditional mean model; ods output CovParms =m0; proc mixed data=alcohol1_pp method=ml ; class id; unconditional: model alcuse = ; random intercept / sub=id; run; * unconditional growth model; ods output covparms = m1; proc mixed data=alcohol1_pp method=ml ; class id; growth: model alcuse = age_14 ; random intercept age_14/type=un sub=id; run; ods output covparms = m2; *subsequent model; proc mixed data=alcohol1_pp method=ml ; title2 "Model D"; class id; model alcuse = coa peer age_14 coa*age_14 peer*age_14; random intercept age_14/type=un sub=id; run; data _null_; set m0; if covparm="Residual" then call symput('sigma0', estimate); run; data _null_; set m1; if covparm="Residual" then call symput('sigma1', estimate); if covparm="UN(1,1)" then call symput('xi01', estimate); if covparm="UN(2,2)" then call symput('xi02', estimate); run; data _null_; set m2; if covparm="UN(1,1)" then call symput('xi1', estimate); if covparm="UN(2,2)" then call symput('xi2', estimate); run; data r2; r2_e = (&sigma0-&sigma1)/&sigma0; r2_0 = (&xi01 - &xi1)/&xi01; r2_1 = (&xi02 - &xi2)/&xi02; run; proc print data = r2; run;Obs r2_e r2_0 r2_1 1 0.39957 0.61415 0.079962
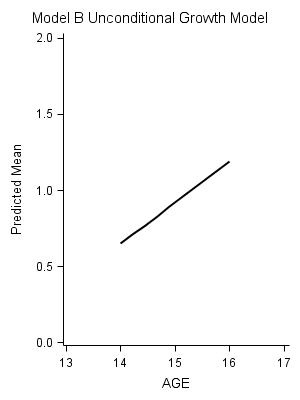
Figure 4.3 on page 99. The first two plots are based on the output data sets created by proc mixed using the outpm option after the model statement. The most right panel has to be created manually, since we have to create a new variable indicating the level of PEER.
ods graphics on /width=3in height=4in border=off;
proc mixed data=alcohol1_pp method=ml ;
class id;
model alcuse = age_14/outpm = mb;
random intercept age_14/type=un sub=id;
run;
proc template;
define style styles.alcohol;
parent=styles.default;
style GraphData1 from _self_/
"LineStyle" = shortdash;
style GraphData2 from _self_/
"LineStyle" = mediumdash;
style GraphData3 from _self_/
"LineStyle" = mediumdashshortdash;
style GraphData4 from _self_/
"LineStyle" = mediumdashshortdash;
end;
run;
ods html style = styles.alcohol;
title "Model B Unconditional Growth Model";
proc sgplot data=mb noautolegend;
xaxis min = 13 max = 17;
yaxis min = 0 max = 2;
reg x=age y=pred /nomarkers lineattrs=(color=black);
run;
proc mixed data=alcohol1_pp method=ml noclprint noinfo covtest;
class id;
model alcuse = coa age_14 coa*age_14/solution notest outpm = mc;
random intercept age_14/type=un sub=id;
run;
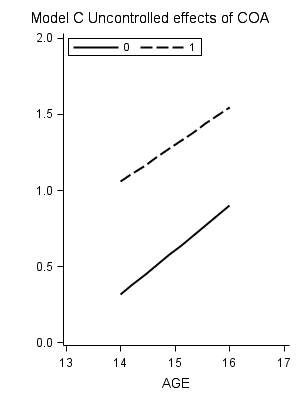
title "Model C Uncontrolled effects of COA";
proc sgplot data=mc ;
xaxis min = 13 max = 17;
yaxis min = 0 max = 2 label=" ";
reg x=age y=pred /group=coa name="s1" nomarkers lineattrs=(color=black) ;
keylegend "s1" / across= 2 location=inside ;
run;
data fig43r;
do age = 14 to 16;
do p = 0 to 1;
do coa = 0 to 1;
if p = 0 then peer = .655;
if P = 1 then peer = 1.381;
alcusehat = -.314 + .571*coa + .695*peer + .425*(age-14) + -.151*(age-14)*peer;
if coa = 0 and p = 0 then coapeer = "L-P, C=0";
if coa = 0 and p = 1 then coapeer = "H-P, C=0";
if coa = 1 and p = 0 then coapeer = "L-P, C=1";
if coa = 1 and p = 1 then coapeer = "H-P, C=1";
output;
end;
end;
end;
run;
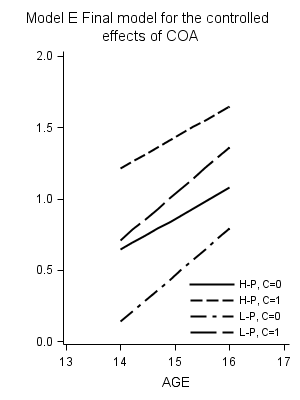
Title "Model E Final model for the controlled effects of COA";
proc sgplot data=fig43r ;
xaxis min = 13 max = 17 label="AGE";
yaxis min = 0 max = 2 label =" ";
reg x=age y=alcusehat / group = coapeer nomarkers name="s1" lineattrs=(color=black);
keylegend "s1" /across=1 location=inside position=bottomright noborder;
run;
Table on the bottom of page 112.
proc sort data = fig43r (where=(age<=15)) out=page112; by p coa age; run;
data page112a; retain initial slope; set page112; lagp = lag(alcusehat); if age=14 then initial = alcusehat; if age = 15 then slope = alcusehat - lagp; drop lagp age; if age = 15; run; proc sort data = page112a; by p coa; proc print data = page112a ; id coapeer; var initial slope; run;
coapeer initial slope
Low Peer , COA=0 0.14123 0.32610 Low Peer , COA=1 0.71223 0.32610 High Peer, COA=0 0.64580 0.21647 High Peer, COA=1 1.21680 0.21647
Test of equation 4.18 on page 123 using model F.
proc mixed data=alcohol1_pp; method=ml; title2 "Model F"; class id; model alcuse = coa cpeer age_14 cpeer*age_14 /solution chisq ; random intercept age_14/type=un sub=id; contrast 'Equation 4.18' intercept 1, age_14 1/ chisq ; run;
The Mixed Procedure
Contrasts
Num Den
Label DF DF Chi-Square F Value Pr > ChiSq Pr > F
Equation 4.18 2 80 51.03 25.51 <.0001 <.0001
Figure 4.4 on page 130.
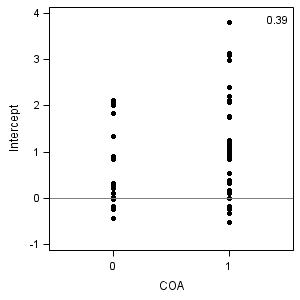
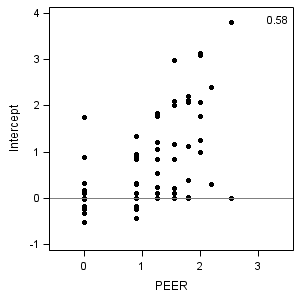
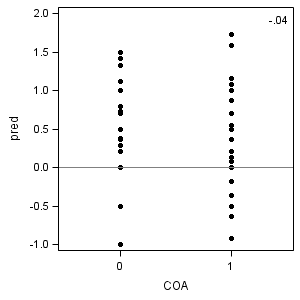
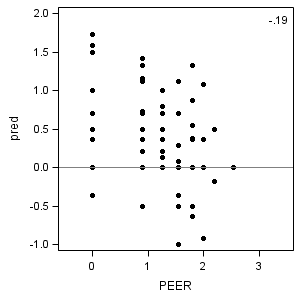
proc sort data = alcohol1_pp out=fig4_4; by id; run; proc reg data = fig4_4 outest=est plots=none noprint; by id; model alcuse = age_14; run; quit; data fig4_4l; merge est(rename=(age_14=pred)) fig4_4; by id; run; ods output PearsonCorr = corr; proc corr data = fig4_4l nosimple noprob; var coa peer; with intercept pred; run;
COA PEER Intercept 0.38867 0.57808 pred -0.04349 -0.19404
data _null_;
set corr;
if _n_ = 1 then do;
call symput('int_coa', put(coa, 4.2));
call symput('int_peer', put(peer, 4.2));
end;
if _n_ = 2 then do;
call symput('pred_coa', put(coa, 4.2));
call symput('pred_peer', put(peer, 4.2));
end;
run;
ods html style=journal2;
ods graphics on /width=3in height=3in border=off;
title;
proc sgplot data = fig4_4l;
xaxis min = -.5 max = 1.5 values=(0,1) VALUESHINT;
yaxis min = -1 max = 4 label="Intercept";
format estimate 3.0;
scatter x = coa y = intercept /markerattrs = (symbol=circlefilled);
refline 0 /axis=y;
inset "&int_coa" /noborder position=topright;
run;
proc sgplot data = fig4_4l;
xaxis min = -.5 max = 1.5 values=(0,1) VALUESHINT;
yaxis min = -1 max = 2 label="pred";
format estimate 3.0;
scatter x = coa y = pred /markerattrs = (symbol=circlefilled);
refline 0 /axis=y;
inset "&pred_coa" /noborder position=topright;
run;
proc sgplot data = fig4_4l;
xaxis min = -.5 max = 3.5 values=(0,1,2,3) VALUESHINT;
yaxis min = -1 max = 4 label="Intercept";
format estimate 3.0;
scatter x = peer y = intercept /markerattrs = (symbol=circlefilled);
refline 0 /axis=y;
inset "&int_peer" /noborder position=topright;
run;
proc sgplot data = fig4_4l ;
xaxis min = -.5 max = 3.5 values=(0,1,2,3) VALUESHINT;
yaxis min = -1 max = 2 label="pred";
format estimate 3.0;
scatter x = peer y = pred /markerattrs = (symbol=circlefilled);
refline 0 /axis=y;
inset "&pred_peer" /noborder position=topright;
run;
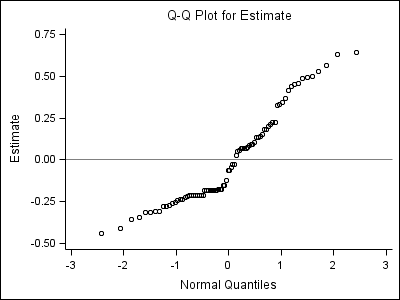
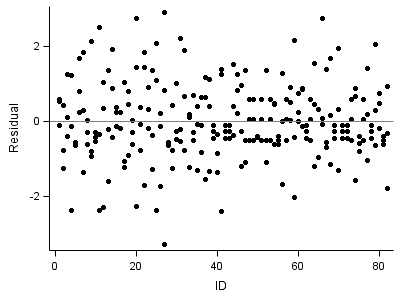
Figure 4.5 on page 131.
proc template; define style MyStyleDefault; parent=Styles.journal2; style Graph from Graph /OutputWidth = 4in OutputHeight=3in ; style GraphWalls from GraphWalls /FrameBorder = off; end; run; ods html style=MystyleDefault;
proc mixed data="c:aldaalcohol1_pp" covtest method=ml; title2 "Model F"; class id; model alcuse = coa cpeer age_14 cpeer*age_14 / outp=fig4_5 solution chisq ; random intercept age_14/type=un sub=id solution; ods output SolutionR = fig4_5a; run;
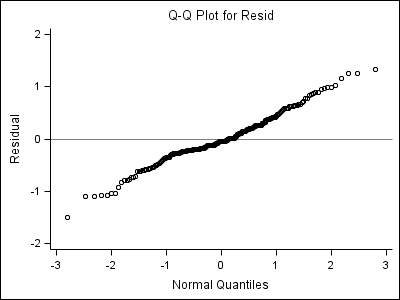
Part 1: Left upper one:
proc univariate data = fig4_5 noprint; var resid; qqplot /vref=0 ; run;
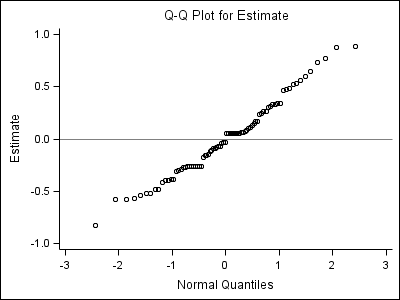
Part 2: Left middle one:
proc univariate data = fig4_5a noprint; where effect = "Intercept"; var estimate; qqplot /vref=0 normal; run;
Part 3: Left lower one:
proc univariate data = fig4_5a noprint; where effect = "AGE_14"; var estimate; qqplot /vref=0 ; run;
Part 4: Right upper one:
proc stdize data = fig4_5 out=fig4_5r; var resid; run; title; proc sgplot data = fig4_5r; scatter x = id y = resid /markerattrs = (symbol=circlefilled); refline 0 /axis=y; run; quit;
Part 5: Right middle one:
proc stdize data = fig4_5a out=fig4_5rm (rename=(estimate = int)); where effect = "Intercept"; var estimate; run;
proc sgplot data = fig4_5rm; format int 3.0; scatter x = id y = int /markerattrs = (symbol=circlefilled); refline 0 /axis=y; run;
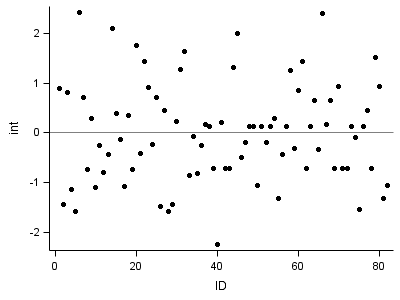
Part 6: Right lower one:
proc stdize data = fig4_5a out=fig4_5rm (rename=(estimate=age)); where effect = "AGE_14"; var estimate; run; proc sgplot data = fig4_5rm; format age 3.0; scatter x = id y= age /markerattrs = (symbol=circlefilled); refline 0 /axis=y; run; quit;
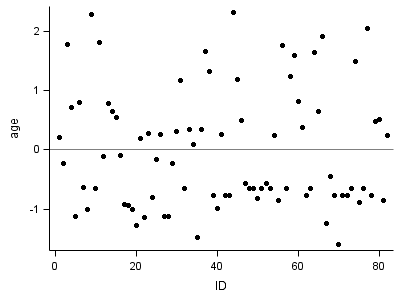
Figure 4.6 on page 133.
Part 1: Left upper plot:
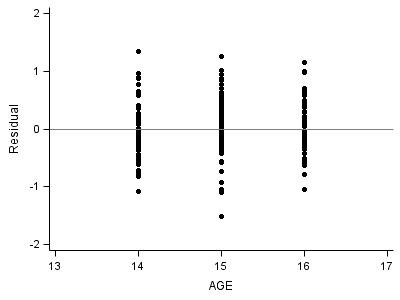
proc sgplot data = fig4_5 ; xaxis min = 13 max = 17; yaxis min = -2 max = 2; scatter x = age y = resid /markerattrs = (symbol=circlefilled); refline 0 /axis=y; run; quit;
Part 2: Left middle plot:
proc sort data = fig4_a;
by id;
proc sort data = alcohol1_pp;
by id;
run;
data fig4_6int;
merge fig4_5a (where=(effect="Intercept"))
alcohol1_pp;
by id;
run;
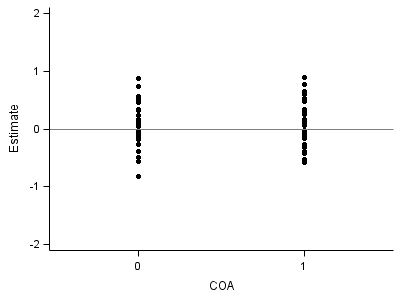
proc sgplot data = fig4_6int;
xaxis min = -.5 max = 1.5 values=(0,1) VALUESHINT;
yaxis min = -2 max = 2;
format estimate 3.0;
scatter x = coa y = estimate /markerattrs = (symbol=circlefilled);
refline 0 /axis=y;
run;
quit;
Part 3: Left lower plot:
data fig4_6age;
merge fig4_5a (where=(effect="AGE_14"))
alcohol1_pp;
by id;
run;
proc sgplot data = fig4_6age;
xaxis min = -.5 max = 1.5 values=(0,1) VALUESHINT;
yaxis min = -2 max = 2 label="AGE_14";
format estimate 3.0;
scatter x = coa y = estimate /markerattrs = (symbol=circlefilled);
refline 0 /axis=y;
run;
quit;
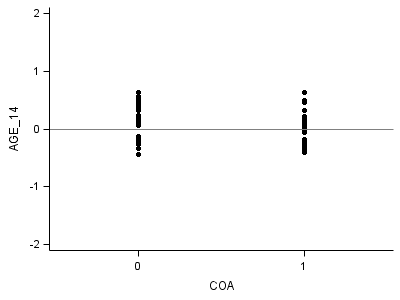
Part 4: Right middle plot:
proc sgplot data = fig4_6int; xaxis min = -.5 max = 3.5 values=(0,1, 2, 3) VALUESHINT; yaxis min = -1 max = 1 ; format estimate 3.0; scatter x = peer y = estimate /markerattrs = (symbol=circlefilled); refline 0 /axis=y; run; quit;
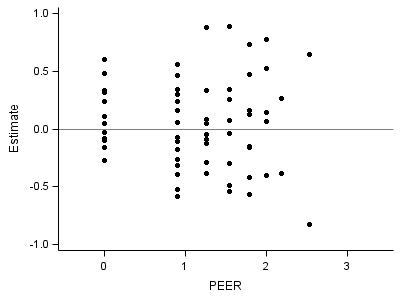
Part 5: Right lower plot:
proc sgplot data = fig4_6age; xaxis min = -.5 max = 3.5 values=(0,1, 2, 3) VALUESHINT; yaxis min = -1 max = 1 ; format estimate 3.0; scatter x = peer y = estimate /markerattrs = (symbol=circlefilled); refline 0 /axis=y; run; quit;
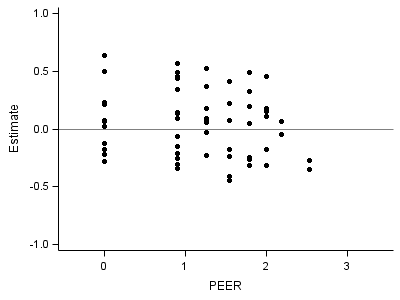
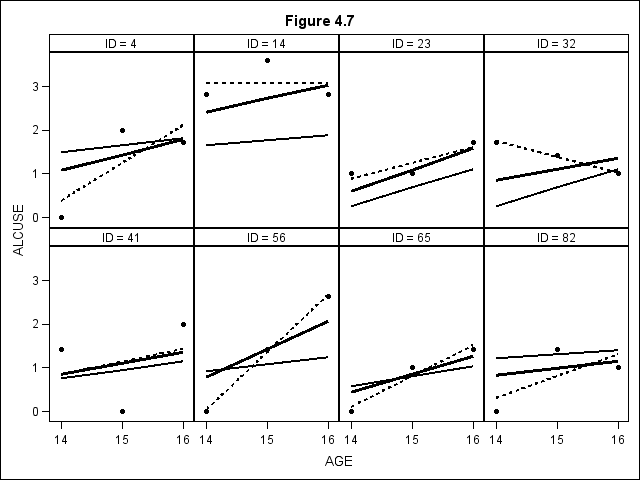
Figure 4.7 on page 136.
proc mixed data=alcohol1_pp covtest method=ml; title2 "Model F"; class id; model alcuse = coa cpeer age_14 cpeer*age_14 /outp=fig4_7p outpm = fig4_7pm solution chisq ; random intercept age_14/type=un sub=id solution; run; proc sort data = fig4_7p; by id; proc sort data = fig4_7pm; by id; run; data fig4_7; merge fig4_7p (rename = (pred=p)) fig4_7pm (rename=(pred=pm)); by id; keep age id p pm alcuse; where id in (4,14,23,32,41,56,65,82); run; proc sort data = fig4_7; by id age; run;
ods graphics on /reset = all; title "Figure 4.7"; proc sgpanel data = fig4_7 noautolegend; panelby id /rows=2 columns=4; reg x = age y = alcuse / markerattrs= (symbol=circlefilled) LINEATTRS = (pattern = 2 COLOR= black); series x = age y = p / LINEATTRS = (pattern = 1 COLOR= black thickness=3); series x = age y = pm / LINEATTRS = (pattern = 1 COLOR= black thickness=2); run;