Note: This page is done using SAS 9.3 and is partly based on SAS code provided by Raymond R. Balise of Stanford University. We thank Raymond R. Balise for sharing his SAS 9.2 code with us.
Table 5.1 on page141.
title1 'Table 5.1 NLSY Reading study: 89 African American children'; proc print data='c:\alda\reading_pp'; where id in (04,27,31,33,41,49,69,77,87); id id; var wave agegrp age piat; run; Table 5.1 NLSY Reading study: 89 African American children ID WAVE AGEGRP AGE PIAT 4 1 6.5 6.0000 18 4 2 8.5 8.5000 31 4 3 10.5 10.6667 50 27 1 6.5 6.2500 19 27 2 8.5 9.1667 36 27 3 10.5 10.9167 57 31 1 6.5 6.3333 18 31 2 8.5 8.8333 31 31 3 10.5 10.9167 51 33 1 6.5 6.3333 18 33 2 8.5 8.9167 34 33 3 10.5 10.7500 29 41 1 6.5 6.3333 18 41 2 8.5 8.7500 28 41 3 10.5 10.8333 36 49 1 6.5 6.5000 19 49 2 8.5 8.7500 32 49 3 10.5 10.6667 48 69 1 6.5 6.6667 26 69 2 8.5 9.1667 47 69 3 10.5 11.3333 45 77 1 6.5 6.8333 17 77 2 8.5 8.0833 19 77 3 10.5 10.0000 28 87 1 6.5 6.9167 22 87 2 8.5 9.4167 49 87 3 10.5 11.5000 64
Figure 5.1 on page 143.
data fig5_1;
set "c:\alda\reading_pp";
if id in (04,27,31,33,41,49,69,77,87);
run;
ods graphics /reset = all;
proc sgpanel data = fig5_1;
panelby id /rows=3 columns=3 ;
colaxis label="Age or age group";
reg x = age y = piat / markerattrs = (symbol = circlefilled color = black)
lineattrs = (color = black pattern = 2) legendlabel = "Age";;
reg x = agegrp y = piat /markerattrs = (symbol = plus color = black)
lineattrs = (color = black pattern = 1) legendlabel = "Age Group";;
run;
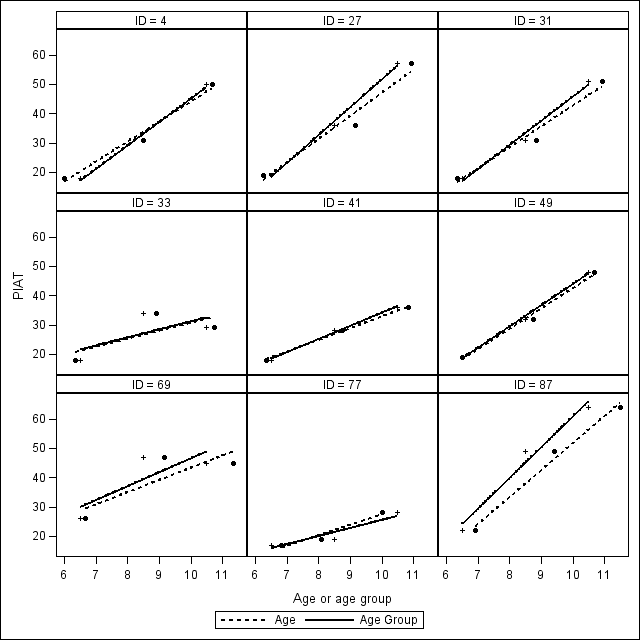
Table 5.2, page 145
data reading1; set 'c:\alda\reading_pp'; cage=age-6.5; cagegrp=agegrp-6.5; run; proc mixed data=reading1 covtest noclprint noinfo noitprint method=ml; title1 'Table 5.2: Alternative representations for the main effect of TIME'; title2 'Unconditional growth model'; title3 'Using AGEGRP-6.5 as a temporal predictor'; class id; model piat=cagegrp / solution notest ddfm=bw; random intercept cagegrp / subject=id type=un; run; proc mixed data=reading1 covtest noclprint noinfo noitprint method=ml; title3 'Using AGE-6.5 as a temporal predictor'; class id; model piat=cage / solution notest ddfm=bw; random intercept cage / subject=id type=un; run;
Table 5.2: Alternative representations for the main effect of TIME Unconditional growth model Using AGEGRP-6.5 as a temporal predictor
The Mixed Procedure
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z
UN(1,1) ID 11.0459 6.0626 1.82 0.0342 UN(2,1) ID 1.6467 2.0630 0.80 0.4248 UN(2,2) ID 4.3975 1.2713 3.46 0.0003 Residual 27.0431 4.0539 6.67 <.0001
Fit Statistics
-2 Log Likelihood 1819.9 AIC (smaller is better) 1831.9 AICC (smaller is better) 1832.3 BIC (smaller is better) 1846.9
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 86.92 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t|
Intercept 21.1629 0.6143 88 34.45 <.0001 cagegrp 5.0309 0.2956 177 17.02 <.0001
Table 5.2: Alternative representations for the main effect of TIME Unconditional growth model Using AGE-6.5 as a temporal predictor
The Mixed Procedure
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z
UN(1,1) ID 5.1064 6.0299 0.85 0.1985 UN(2,1) ID 2.3667 1.8022 1.31 0.1891 UN(2,2) ID 3.3011 1.0145 3.25 0.0006 Residual 27.4476 4.3720 6.28 <.0001
Fit Statistics
-2 Log Likelihood 1803.9 AIC (smaller is better) 1815.9 AICC (smaller is better) 1816.2 BIC (smaller is better) 1830.8
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 88.91 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t|
Intercept 21.0608 0.5593 88 37.65 <.0001 cage 4.5400 0.2606 177 17.42 <.0001
Table 5.3 on page 147.
title1 'Table 5.3: Excerpts from the person-period data set for the high school dropout study'; proc print data='c:\alda\wages_pp'; where id in (206,332,1028); id id; var exper lnw black hgc uerate; run; Table 5.3: Excerpts from the person-period data set for the high school dropout ID EXPER LNW BLACK HGC UERATE 206 1.874 2.028 0 10 9.200 206 2.814 2.297 0 10 11.000 206 4.314 2.482 0 10 6.295 332 0.125 1.630 0 8 7.100 332 1.625 1.476 0 8 9.600 332 2.413 1.804 0 8 7.200 332 3.393 1.439 0 8 6.195 332 4.470 1.748 0 8 5.595 332 5.178 1.526 0 8 4.595 332 6.082 2.044 0 8 4.295 332 7.043 2.179 0 8 3.395 332 8.197 2.186 0 8 4.395 332 9.092 4.035 0 8 6.695 1028 0.004 0.872 1 8 9.300 1028 0.035 0.903 1 8 7.400 1028 0.515 1.389 1 8 7.300 1028 1.483 2.324 1 8 7.400 1028 2.141 1.484 1 8 6.295 1028 3.161 1.705 1 8 5.895 1028 4.103 2.343 1 8 6.900
Table 5.4 on page 149.
title1 'Table 5.4: Taxonomy of growth models to high school dropout wage data--Full ML'; proc mixed data='c:\alda\wages_pp' method=ml covtest noclprint noinfo; title2 'Model A: Unconditional growth model'; class id; model lnw=exper / solution notest; random intercept exper / subject=id type=un; run; proc mixed data='c:\alda\wages_pp' method=ml covtest noclprint noinfo; title2 'Model B: Conditional growth model'; title3 'effects of Black and HGC on both initial status and growth rate'; class id; model lnw=exper hgc_9 hgc_9*exper black black*exper/solution notest; random intercept exper/subject=id type=un; run; proc mixed data='c:\alda\wages_pp' method=ml covtest noclprint noinfo; title2 'Model C: conditional growth model'; title3 'HGC predicts initial status/BLACK predicts growth rate'; class id; model lnw=exper hgc_9 black*exper /solution notest; random intercept exper/subject=id type=un; run; Table 5.4: Taxonomy of growth models to high school dropout wage data--Full ML Model A: Unconditional growth model
The Mixed Procedure
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z
UN(1,1) ID 0.05427 0.005001 10.85 <.0001 UN(2,1) ID -0.00291 0.000869 -3.35 0.0008 UN(2,2) ID 0.001726 0.000220 7.84 <.0001 Residual 0.09511 0.001944 48.92 <.0001
Fit Statistics -2 Log Likelihood 4921.4 AIC (smaller is better) 4933.4 AICC (smaller is better) 4933.4 BIC (smaller is better) 4962.1
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 1580.05 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t| Intercept 1.7156 0.01080 887 158.90 <.0001 EXPER 0.04568 0.002341 850 19.51 <.0001
Table 5.4: Taxonomy of growth models to high school dropout wage data--Full ML Model B: Conditional growth model effects of Black and HGC on both initial status and growth rate
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z UN(1,1) ID 0.05175 0.004868 10.63 <.0001 UN(2,1) ID -0.00285 0.000844 -3.38 0.0007 UN(2,2) ID 0.001635 0.000214 7.65 <.0001 Residual 0.09520 0.001946 48.91 <.0001
Fit Statistics -2 Log Likelihood 4873.8 AIC (smaller is better) 4893.8 AICC (smaller is better) 4893.8 BIC (smaller is better) 4941.6
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 1465.80 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t| Intercept 1.7171 0.01254 885 136.91 <.0001 EXPER 0.04934 0.002631 847 18.75 <.0001 HGC_9 0.03492 0.007881 4664 4.43 <.0001 EXPER*HGC_9 0.001280 0.001723 4664 0.74 0.4576 BLACK 0.01540 0.02393 4664 0.64 0.5200 EXPER*BLACK -0.01821 0.005498 4664 -3.31 0.0009
Table 5.4: Taxonomy of growth models to high school dropout wage data--Full ML Model C: conditional growth model HGC predicts initial status/BLACK predicts growth rate
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z UN(1,1) ID 0.05183 0.004873 10.64 <.0001 UN(2,1) ID -0.00288 0.000845 -3.41 0.0007 UN(2,2) ID 0.001646 0.000214 7.69 <.0001 Residual 0.09518 0.001945 48.92 <.0001
Fit Statistics -2 Log Likelihood 4874.7 AIC (smaller is better) 4890.7 AICC (smaller is better) 4890.7 BIC (smaller is better) 4929.0
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 1474.50 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t| Intercept 1.7215 0.01070 886 160.93 <.0001 EXPER 0.04885 0.002513 849 19.44 <.0001 HGC_9 0.03836 0.006433 4663 5.96 <.0001 EXPER*BLACK -0.01612 0.004511 4663 -3.57 0.0004
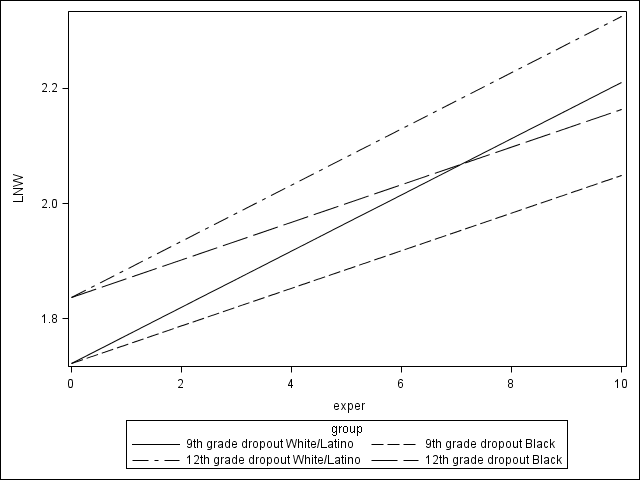
Figure 5.2 on page 150.
data fig5_2s; input exper hgc_9 black group $8-40; datalines; 0 0 0 9th grade dropout White/Latino 10 0 0 9th grade dropout White/Latino 0 0 1 9th grade dropout Black 10 0 1 9th grade dropout Black 0 3 0 12th grade dropout White/Latino 10 3 0 12th grade dropout White/Latino 0 3 1 12th grade dropout Black 10 3 1 12th grade dropout Black ; run; data fig5_2sa; set fig5_2s; model1 = 1.7215 + 0.04885* exper + 0.03836*hgc_9 + -0.01612*exper*black; run;
proc sgplot data= fig5_2sa; label model1 = "LNW"; series x = exper y = model1 /group=group; run;
Table 5.5 on page 154.
title1 'Table 5.5: Severely unbalanced data: Alternative approaches to model fitting'; title2 'Model C of Table 5.4'; proc mixed data='c:\alda\wages_small_pp' method=ml covtest noclprint noinfo; title3 'Approach A: Default method'; class id; model lnw=exper hgc_9 black*exper /solution notest; random intercept exper/subject=id type=un; run; proc mixed data='c:\alda\wages_small_pp' method=ml covtest noclprint noinfo nobound; title3 'Approach B: Removing boundary constraints to allow negative variances'; class id; model lnw=exper hgc_9 black*exper /solution notest; random intercept exper/subject=id type=un; run; proc mixed data='c:\alda\wages_small_pp' method=ml covtest noclprint noinfo; title3 'Approach C: Fixing rates of change'; class id; model lnw=exper hgc_9 black*exper /solution notest; random intercept /subject=id type=un; run; Table 5.5: Severely unbalanced data: Alternative approaches to model fitting Model C of Table 5.4 Approach A: Default method
The Mixed Procedure
Iteration History
Iteration Evaluations -2 Log Like Criterion
0 1 307.58403963
1 4 285.02372722 .
2 1 283.93857489 0.00070544
3 1 283.86897267 0.00000402
4 1 283.86859250 0.00000000
Convergence criteria met.
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z UN(1,1) ID 0.08182 0.03344 2.45 0.0072 UN(2,1) ID 0.000627 0.006792 0.09 0.9264 UN(2,2) ID 7.54E-35 . . . Residual 0.1150 0.01475 7.80 <.0001
Fit Statistics -2 Log Likelihood 283.9 AIC (smaller is better) 297.9 AICC (smaller is better) 298.3 BIC (smaller is better) 317.6
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
2 23.72 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t| Intercept 1.7373 0.04758 122 36.52 <.0001 EXPER 0.05159 0.02110 84 2.45 0.0165 HGC_9 0.04616 0.02447 47 1.89 0.0654 EXPER*BLACK -0.05963 0.03479 47 -1.71 0.0932
Table 5.5: Severely unbalanced data: Alternative approaches to model fitting Model C of Table 5.4 Approach B: Removing boundary constraints to allow negative variances
The Mixed Procedure
Iteration History
Iteration Evaluations -2 Log Like Criterion
0 1 307.58403963
1 2 284.56884709 5.60876702
2 1 284.25194563 35.06944214
3 1 283.92785064 5019.4659324
4 1 283.52412688 42196.186854
5 1 282.74158921 497747.83733
6 1 281.41649752 10711506.626
7 1 279.61403087 437866210.81
8 1 277.62479582 23604297296
9 1 275.60074420 1.3418459E12
10 1 273.57182583 7.6858612E13
11 1 271.54226352 4.4071347E15
12 1 269.51261608 2.527673E17
13 1 267.48295914 1.4498933E19
14 1 265.45328889 8.3175546E20
15 1 263.42383149 4.771923E22
16 1 261.39794939 2.7390031E24
17 1 260.81549327 8.5330494E24
18 1 260.24522738 2.6613477E25
19 1 259.67583657 8.2813409E25
20 0 259.67583657 8.2813409E25
21 0 259.67583657 8.2813409E25
22 0 259.67583657 8.2813409E25
23 0 259.67583657 8.2813409E25
WARNING: Did not converge.
Covariance Parameter Values
At Last Iteration
Cov Parm Subject Estimate
UN(1,1) ID 0.02665 UN(2,1) ID 0.01954 UN(2,2) ID -0.00718 Residual 0.1374
Table 5.5: Severely unbalanced data: Alternative approaches to model fitting Model C of Table 5.4 Approach C: Fixing rates of change
The Mixed Procedure
Iteration History
Iteration Evaluations -2 Log Like Criterion 0 1 307.58403963 1 2 283.98842625 0.00110656 2 1 283.87813973 0.00000977 3 1 283.87721345 0.00000000
Convergence criteria met.
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z UN(1,1) ID 0.08424 0.02119 3.98 <.0001 Residual 0.1148 0.01455 7.89 <.0001
Fit Statistics -2 Log Likelihood 283.9 AIC (smaller is better) 295.9 AICC (smaller is better) 296.2 BIC (smaller is better) 312.8
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
1 23.71 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t| Intercept 1.7373 0.04775 122 36.38 <.0001 EXPER 0.05178 0.02093 131 2.47 0.0147 HGC_9 0.04576 0.02450 131 1.87 0.0640 EXPER*BLACK -0.06007 0.03458 131 -1.74 0.0847
Table 5.6 on page 161.
title1 'Table 5.6: Excerpts from the person-period data set for the unemployment study'; proc print data='c:\alda\unemployment_pp'; where id in (7589,55697,67641,65441,53782); id id; var months cesd unemp; run;
Table 5.6: Excerpts from the person-period data set for the unemployment study
ID MONTHS CESD UNEMP 7589 1.3142 36 1 7589 5.0924 40 1 7589 11.7947 39 1 53782 0.4271 22 1 53782 4.2382 15 0 53782 11.0719 21 1 55697 1.3470 7 1 55697 5.7823 4 1 65441 1.0842 27 1 65441 4.6982 15 1 65441 11.2690 7 0 67641 0.3285 32 1 67641 4.1068 9 0 67641 10.9405 10 0
Table 5.7 on page 163.
title1 'Table 5.7: Taxonomy of models of unemployment data'; proc mixed data='c:\alda\unemployment_pp' covtest noclprint noitprint noinfo method=ml; Title2 'Model A: Initial growth model'; class id; model cesd=months / solution notest; random intercept months / subject=id type=un; run; proc mixed data='c:\alda\unemployment_pp' covtest noclprint noitprint noinfo method=ml; Title2 'Model B: Main effect of unemployment'; class id; model cesd=months unemp / solution notest; random intercept months / subject=id type=un; run; proc mixed data='c:\alda\unemployment_pp' covtest noclprint noitprint noinfo method=ml; Title2 'Model C: Effect of unemployment on initial status and growth rate'; class id; model cesd=months unemp unemp*months / solution notest; random intercept months / subject=id type=un; run; proc mixed data='c:\alda\unemployment_pp' covtest noclprint noitprint noinfo method=ml; Title2 'Model D: Allowing unemp to have both fix and random effects'; class id; model cesd=unemp unemp*months / solution notest; random intercept unemp unemp*months / subject=id type=un; run; Table 5.7: Taxonomy of models of unemployment data Model A: Initial growth model
The Mixed Procedure
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z UN(1,1) ID 86.8483 14.9631 5.80 <.0001 UN(2,1) ID -3.0572 1.3846 -2.21 0.0272 UN(2,2) ID 0.3550 0.1845 1.92 0.0272 Residual 68.8502 6.6027 10.43 <.0001
Fit Statistics -2 Log Likelihood 5133.1 AIC (smaller is better) 5145.1 AICC (smaller is better) 5145.3 BIC (smaller is better) 5166.4
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 106.52 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t| Intercept 17.6694 0.7756 253 22.78 <.0001 MONTHS -0.4220 0.08298 226 -5.09 <.0001
Table 5.7: Taxonomy of models of unemployment data Model B: Main effect of unemployment
The Mixed Procedure
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z UN(1,1) ID 93.5189 14.8202 6.31 <.0001 UN(2,1) ID -3.8941 1.3703 -2.84 0.0045 UN(2,2) ID 0.4647 0.1798 2.58 0.0049 Residual 62.3875 6.0132 10.38 <.0001
Fit Statistics -2 Log Likelihood 5107.6 AIC (smaller is better) 5121.6 AICC (smaller is better) 5121.8 BIC (smaller is better) 5146.4
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 114.84 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t| Intercept 12.6656 1.2421 253 10.20 <.0001 MONTHS -0.2020 0.09332 226 -2.16 0.0315 UNEMP 5.1113 0.9888 192 5.17 <.0001
Table 5.7: Taxonomy of models of unemployment data Model C: Effect of unemployment on initial status and growth rate
The Mixed Procedure
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z UN(1,1) ID 93.7132 14.7771 6.34 <.0001 UN(2,1) ID -3.8732 1.3588 -2.85 0.0044 UN(2,2) ID 0.4512 0.1773 2.54 0.0055 Residual 62.0312 5.9655 10.40 <.0001
Fit Statistics -2 Log Likelihood 5103.0 AIC (smaller is better) 5119.0 AICC (smaller is better) 5119.3 BIC (smaller is better) 5147.3
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 116.31 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t| Intercept 9.6167 1.8893 253 5.09 <.0001 MONTHS 0.1620 0.1937 226 0.84 0.4036 UNEMP 8.5291 1.8779 191 4.54 <.0001 MONTHS*UNEMP -0.4652 0.2172 191 -2.14 0.0335
Table 5.7: Taxonomy of models of unemployment data Model D: Allowing unemp to have both fix and random effects
The Mixed Procedure
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z UN(1,1) ID 41.5205 12.0291 3.45 0.0003 UN(2,1) ID 9.1551 11.0161 0.83 0.4059 UN(2,2) ID 40.4542 20.4989 1.97 0.0242 UN(3,1) ID 2.3548 1.6302 1.44 0.1486 UN(3,2) ID -7.2074 2.1530 -3.35 0.0008 UN(3,3) ID 0.7063 0.2593 2.72 0.0032 Residual 62.4345 6.5923 9.47 <.0001
Fit Statistics -2 Log Likelihood 5093.6 AIC (smaller is better) 5113.6 AICC (smaller is better) 5113.9 BIC (smaller is better) 5149.0
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
6 126.32 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t| Intercept 11.2666 0.7690 253 14.65 <.0001 UNEMP 6.8795 0.9133 121 7.53 <.0001 UNEMP*MONTHS -0.3254 0.1105 164 -2.94 0.0037
Figure 5.3 on page 165. The plot is based on the main effect model: Model B in the previous example.
proc mixed data = unemployment_pp method = ml;
class id;
model cesd = months unemp/ solution;
random intercept months / subject = id type = un;
store out = unemp_plm;
run;
proc format ;
value plot 1 = "Remains unemployed"
2 = "Reemployed at 5 months"
3 = "Reemployed at 10 months"
4 = "Reemployed at 5, unemped at 10";
run;
data preddata;
input months unemp plot;
format plot plot.;
datalines;
0 1 1
5 1 1
10 1 1
13 1 1
0 1 2
5 1 2
5 0 2
10 0 2
13 0 2
0 1 3
5 1 3
10 1 3
10 0 3
13 0 3
0 1 4
5 1 4
5 0 4
10 0 4
10 1 4
13 1 4
;
run;
proc plm source = unemp_plm;
score data = preddata out = plotdata;
run;
proc sgpanel data = plotdata;
panelby plot;
series x = months y = Predicted;
rowaxis max = 20 min = 5;
colaxis min = -1 max = 15;
run;
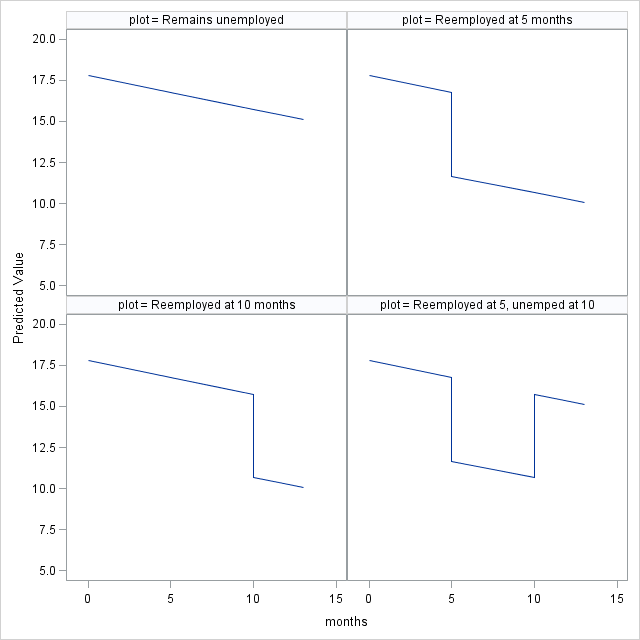
Figure 5.4 on page 167. Based on Model B, Model C and Model D, we generate predicted values for unemp = 0 and unemp =1 cases. The rest is to set up the options to plot each one of them against the time variable. A lot of the code is for setting up the titles, legend and combining the three plots into one.
title;
proc format ;
value plot 1 = "Model B: Main effects"
2 = "Model C: Interaction"
3 = "Model D: Constraint";
run;
data preddata;
do i = 0 to 14;
months = i;
unemp = 0;
output;
end;
do i = 0 to 14;
months = i;
unemp = 1;
output;
end;
run;
*model B;
proc mixed data = unemployment_pp method = ml;
class id;
model cesd = months unemp/ solution;
random intercept months / subject = id type = un;
store out = bplm;
run;
proc plm source = bplm;
score data = preddata out = bplot;
run;
data bplot;
set bplot;
plot = 1;
run;
*model C;
proc mixed data = unemployment_pp method = ml;
class id;
model cesd = months|unemp / solution;
random intercept months / subject = id type = un;
store out = cplm;
run;
proc plm source = cplm;
score data = preddata out = cplot;
run;
data cplot;
set cplot;
plot = 2;
run;
*model D;
proc mixed data = unemployment_pp method = ml;
class id;
model cesd = unemp unemp*months / solution;
random intercept unemp months*unemp / subject = id type = un;
store out = dplm;
run;
proc plm source = dplm;
score data = preddata out = dplot;
run;
*plot;
data dplot;
set dplot;
plot = 3;
run;
data fig53;
set bplot cplot dplot;
format plot plot.;
run;
proc sgpanel data = fig53;
panelby plot / layout = columnlattice;
series x = months y = Predicted / group = unemp;
rowaxis max = 20 min = 5 label = "CES-D";
colaxis min = -1 max = 15 label = "Months since job loss";
run;
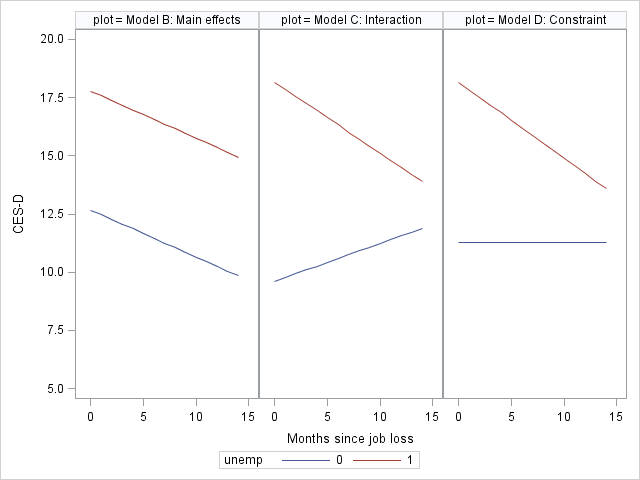
Table 5.8 on page 175.
title1 'Table 5.8: High school dropout wage data--Effects of time-varying unemployment rate'; proc mixed data='c:\alda\wages_pp' method=ml covtest noclprint noinfo; title2 'Model A: Unemployment rate centered around 7'; class id; model lnw=hgc_9 ue_7 exper black*exper / solution notest; random intercept exper/subject=id type=un; run; proc mixed data='c:\alda\wages_pp' method=ml covtest noclprint noinfo; title2 'Model B: Within context centering'; class id; model lnw=hgc_9 ue_mean ue_person_centered exper black*exper / solution notest; random intercept exper/subject=id type=un; run; proc mixed data='c:\alda\wages_pp' method=ml covtest noclprint noinfo; title2 'Model C: Centering on time-1'; class id; model lnw=hgc_9 ue1 ue_centert1 exper black*exper / solution notest; random intercept exper / subject=id type=un; run;
Table 5.8: High school dropout wage data--Effects of time-varying unemployment rate Model A: Unemployment rate centered around 7
The Mixed Procedure
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z UN(1,1) ID 0.05064 0.004808 10.53 <.0001 UN(2,1) ID -0.00291 0.000838 -3.47 0.0005 UN(2,2) ID 0.001631 0.000213 7.68 <.0001 Residual 0.09480 0.001938 48.91 <.0001
Fit Statistics -2 Log Likelihood 4830.5 AIC (smaller is better) 4848.5 AICC (smaller is better) 4848.5 BIC (smaller is better) 4891.6
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 1423.34 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t| Intercept 1.7490 0.01140 886 153.43 <.0001 HGC_9 0.04001 0.006363 4662 6.29 <.0001 UE_7 -0.01195 0.001792 4662 -6.67 <.0001 EXPER 0.04405 0.002603 849 16.92 <.0001 EXPER*BLACK -0.01818 0.004483 4662 -4.06 <.0001
Table 5.8: High school dropout wage data--Effects of time-varying unemployment r Model B: Within context centering
The Mixed Procedure
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z UN(1,1) ID 0.05101 0.004841 10.54 <.0001 UN(2,1) ID -0.00302 0.000843 -3.59 0.0003 UN(2,2) ID 0.001628 0.000212 7.67 <.0001 Residual 0.09480 0.001938 48.91 <.0001
Fit Statistics -2 Log Likelihood 4827.0 AIC (smaller is better) 4847.0 AICC (smaller is better) 4847.0 BIC (smaller is better) 4894.9
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 1407.18 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t| Intercept 1.8743 0.02952 885 63.48 <.0001 HGC_9 0.04017 0.006351 4662 6.33 <.0001 UE_MEAN -0.01771 0.003520 4662 -5.03 <.0001 UE_PERSON_CENTERED -0.00990 0.002097 4662 -4.72 <.0001 EXPER 0.04506 0.002650 849 17.00 <.0001 EXPER*BLACK -0.01887 0.004477 4662 -4.22 <.0001
Table 5.8: High school dropout wage data--Effects of time-varying unemployment r Model C: Centering on time-1
The Mixed Procedure
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z UN(1,1) ID 0.05028 0.004789 10.50 <.0001 UN(2,1) ID -0.00290 0.000838 -3.46 0.0005 UN(2,2) ID 0.001635 0.000213 7.68 <.0001 Residual 0.09477 0.001937 48.92 <.0001
Fit Statistics -2 Log Likelihood 4825.8 AIC (smaller is better) 4845.8 AICC (smaller is better) 4845.9 BIC (smaller is better) 4893.7
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 1423.82 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t| Intercept 1.8693 0.02603 886 71.81 <.0001 HGC_9 0.03993 0.006349 4661 6.29 <.0001 UE1 -0.01618 0.002648 4661 -6.11 <.0001 UE_CENTERT1 -0.01031 0.001944 4661 -5.30 <.0001 EXPER 0.04476 0.002625 849 17.06 <.0001 EXPER*BLACK -0.01832 0.004484 4661 -4.09 <.0001
Table 5.10 on page 184.
title1 'Table 5.10: Alternative parameterizations for the main effect
of TIME in the antidepressant trial';
proc mixed data='c:\alda\medication_pp' noclprint noinfo method=ml covtest;
title2 'Model A: TIME';
class id;
model pos = treat time treat*time / solution ddfm=bw notest;
random intercept time / subject=id type=un;
run;
proc mixed data='c:\alda\medication_pp' noclprint noinfo Method=ml covtest;
title2 'Model B: TIME-3.33';
class id;
model pos = treat time333 treat*time333 / solution ddfm=bw notest;
random intercept time333 / subject=id type=un;
run;
proc mixed data='c:\alda\medication_pp' noclprint noinfo Method=ml covtest;
title2 'Model C: TIME-6.67';
class id;
model pos = treat time667 treat*time667 / solution ddfm=bw notest;
random intercept time667 / subject=id type=un;
run;
Table 5.10: Alternative parameterizations for the main effect of TIME in the ant
Model A: TIME
Covariance Parameter Estimates
Standard Z
Cov Parm Subject Estimate Error Value Pr Z
UN(1,1) ID 2111.33 420.19 5.02 <.0001
UN(2,1) ID -121.62 59.0314 -2.06 0.0394
UN(2,2) ID 63.7351 14.2712 4.47 <.0001
Residual 1229.93 52.0915 23.61 <.0001
Fit Statistics -2 Log Likelihood 12680.5 AIC (smaller is better) 12696.5 AICC (smaller is better) 12696.6 BIC (smaller is better) 12713.7
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 971.31 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t| Intercept 167.46 9.3261 62 17.96 <.0001 TREAT -3.1093 12.3324 62 -0.25 0.8018 TIME -2.4181 1.7308 1176 -1.40 0.1627 TREAT*TIME 5.5368 2.2778 1176 2.43 0.0152
Table 5.10: Alternative parameterizations for the main effect of TIME in the ant Model B: TIME-3.33
The Mixed Procedure
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z UN(1,1) ID 2008.72 367.24 5.47 <.0001 UN(2,1) ID 90.8341 52.4581 1.73 0.0834 UN(2,2) ID 63.7351 14.2712 4.47 <.0001 Residual 1229.93 52.0915 23.61 <.0001
Fit Statistics -2 Log Likelihood 12680.5 AIC (smaller is better) 12696.5 AICC (smaller is better) 12696.6 BIC (smaller is better) 12713.7
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 971.31 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t| Intercept 159.40 8.7644 62 18.19 <.0001 TREAT 15.3467 11.5445 62 1.33 0.1886 TIME333 -2.4181 1.7308 1176 -1.40 0.1627 TREAT*TIME333 5.5368 2.2778 1176 2.43 0.0152
Table 5.10: Alternative parameterizations for the main effect of TIME in the ant Model C: TIME-6.67
The Mixed Procedure
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z UN(1,1) ID 3322.45 632.11 5.26 <.0001 UN(2,1) ID 303.28 80.9007 3.75 0.0002 UN(2,2) ID 63.7351 14.2712 4.47 <.0001 Residual 1229.93 52.0915 23.61 <.0001
Fit Statistics -2 Log Likelihood 12680.5 AIC (smaller is better) 12696.5 AICC (smaller is better) 12696.6 BIC (smaller is better) 12713.7
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 971.31 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t| Intercept 151.34 11.5424 62 13.11 <.0001 TREAT 33.8028 15.1580 62 2.23 0.0294 TIME667 -2.4181 1.7308 1176 -1.40 0.1627 TREAT*TIME667 5.5368 2.2778 1176 2.43 0.0152
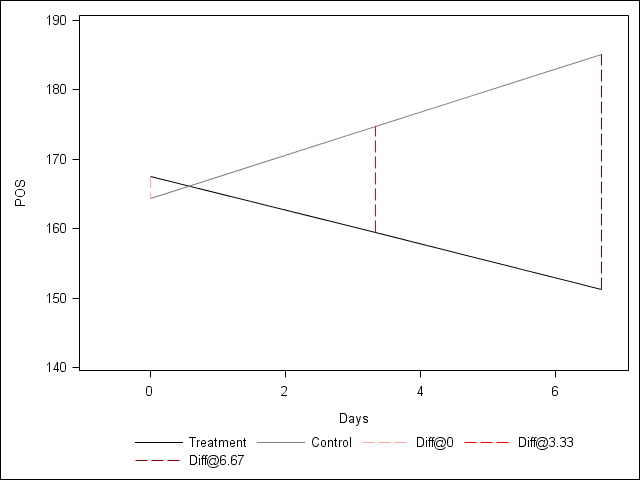
Figure 5.5 on page 185.
data preddata; input time treat line $16. ; datalines; 0 0 Treatment 3.33 0 Treatment 6.67 0 Treatment 0 1 Control 3.33 1 Control 6.67 1 Control 0 0 Diff@0 0 1 Diff@0 3.33 0 Diff@3.33 3.33 1 Diff@3.33 6.67 0 Diff@6.67 6.67 1 Diff@6.67 ; run; proc mixed data = medication_pp method = ml; class id; model pos = treat|time / solution; random intercept time / subject = id type=un; store out=medplm; run; proc plm source = medplm; score out = medplot data = preddata; run; proc template; define style newstyle; style GraphData1 / LineStyle = 1 Contrastcolor = black; style GraphData2 / LineStyle = 1 Contrastcolor = gray; style GraphData3 / LineStyle = 4 Contrastcolor = very light red; style GraphData4 from GraphData3 / Contrastcolor = red; style GraphData5 from GraphData3 / Contrastcolor = very dark red; end; run; ods html style = newstyle; proc sgplot data = medplot noautolegend; series x = time y = Predicted / group = line; xaxis min = -1 max = 7 label = "Days"; yaxis min = 140 max = 190 label = "POS"; keylegend / noborder location = outside; run;
Page 188 on modeling initial and final status.
proc mixed data='c:\alda\medication_pp' noclprint noinfo Method=ml covtest; title2 'Model in Text: Initial and final status model'; class id; model pos = Initial treat*initial final treat*final / solution noint ddfm=bw notest; random initial final / subject=id type=un gcorr; run; Model in Text: Initial and final status model
The Mixed Procedure
Iteration History
Iteration Evaluations -2 Log Like Criterion
0 1 13651.76032736
1 2 12680.45210673 0.00000011
2 1 12680.45155817 0.00000000
Convergence criteria met.
Estimated G Correlation Matrix
Row Effect ID Col1 Col2
1 INITIAL 1 1.0000 0.4910 2 FINAL 1 0.4910 1.0000
Covariance Parameter Estimates
Standard Z Cov Parm Subject Estimate Error Value Pr Z
UN(1,1) ID 2111.33 420.19 5.02 <.0001 UN(2,1) ID 1300.56 392.77 3.31 0.0009 UN(2,2) ID 3322.45 632.11 5.26 <.0001 Residual 1229.93 52.0915 23.61 <.0001
Fit Statistics
-2 Log Likelihood 12680.5 AIC (smaller is better) 12696.5 AICC (smaller is better) 12696.6 BIC (smaller is better) 12713.7
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 971.31 <.0001
Solution for Fixed Effects
Standard Effect Estimate Error DF t Value Pr > |t|
INITIAL 167.46 9.3261 1174 17.96 <.0001 INITIAL*TREAT -3.1093 12.3324 1174 -0.25 0.8010 FINAL 151.34 11.5424 1174 13.11 <.0001 TREAT*FINAL 33.8028 15.1580 1174 2.23 0.0259