4.2 Variable selection
page 105 Table 4.1 Simple logistic regression models for the UIS (n = 575).
NOTE: We have bolded the relevant output.
data uis41;
set 'd:hosmerdatauis';
run;
proc genmod data=uis41 descending;
model dfree = age / dist=bin link=logit waldci;
estimate '10 year increase in age' age 10 /exp ;
run;
The GENMOD Procedure
Model Information
Data Set WORK.UIS41
Distribution Binomial
Link Function Logit
Dependent Variable DFREE
Observations Used 575
Probability Modeled Pr( DFREE = 1 )
Response Profile
Ordered Ordered
Level Value Count
1 0 428
2 1 147
Parameter Information
Parameter Effect
Prm1 Intercept
Prm2 AGE
Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF
Deviance 573 652.3309 1.1384
Scaled Deviance 573 652.3309 1.1384
Pearson Chi-Square 573 575.1709 1.0038
Scaled Pearson X2 573 575.1709 1.0038
Log Likelihood -326.1654
Algorithm converged.
Analysis Of Parameter Estimates
Standard Wald 95% Confidence Chi-
Parameter DF Estimate Error Limits Square Pr > ChiSq
Intercept 1 -1.6602 0.5111 -2.6619 -0.6585 10.55 0.0012
AGE 1 0.0182 0.0153 -0.0119 0.0482 1.40 0.2363
Scale 0 1.0000 0.0000 1.0000 1.0000
NOTE: The scale parameter was held fixed.
The GENMOD Procedure
Contrast Estimate Results
Standard Chi-
Label Estimate Error Alpha Confidence Limits Square Pr > ChiSq
10 year increase in age 0.1817 0.1534 0.05 -0.1190 0.4825 1.40 0.2363
Exp(10 year increase in age) 1.1993 0.1840 0.05 0.8878 1.6201
proc genmod data=uis41 descending;
model dfree = beck / dist=bin link=logit waldci;
estimate '5 point increase in beck' beck 5 /exp ;
run;
The GENMOD Procedure
Model Information
Data Set WORK.UIS41
Distribution Binomial
Link Function Logit
Dependent Variable DFREE
Observations Used 575
Probability Modeled Pr( DFREE = 1 )
Response Profile
Ordered Ordered
Level Value Count
1 0 428
2 1 147
Parameter Information
Parameter Effect
Prm1 Intercept
Prm2 BECK
Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF
Deviance 573 653.0924 1.1398
Scaled Deviance 573 653.0924 1.1398
Pearson Chi-Square 573 575.1216 1.0037
Scaled Pearson X2 573 575.1216 1.0037
Log Likelihood -326.5462
Algorithm converged.
Analysis Of Parameter Estimates
Standard Wald 95% Confidence Chi-
Parameter DF Estimate Error Limits Square Pr > ChiSq
Intercept 1 -0.9273 0.2003 -1.3199 -0.5347 21.43 <.0001
BECK 1 -0.0082 0.0103 -0.0285 0.0120 0.63 0.4265
Scale 0 1.0000 0.0000 1.0000 1.0000
NOTE: The scale parameter was held fixed.
The GENMOD Procedure
Contrast Estimate Results
Standard Chi-
Label Estimate Error Alpha Confidence Limits Square
5 point increase in beck -0.0411 0.0517 0.05 -0.1425 0.0602 0.63
Exp(5 point increase in beck) 0.9597 0.0496 0.05 0.8672 1.0621
Contrast Estimate Results
Label Pr > ChiSq
5 point increase in beck 0.4265
Exp(5 point increase in beck)
proc logistic data=uis41 desc;
model dfree = ndrugtx;
run;
The LOGISTIC Procedure
Model Information
Data Set WORK.UIS41
Response Variable DFREE
Number of Response Levels 2
Number of Observations 575
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value DFREE Frequency
1 1 147
2 0 428
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 655.729 645.890
SC 660.083 654.598
-2 Log L 653.729 641.890
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 11.8392 1 0.0006
Score 9.7585 1 0.0018
Wald 9.2203 1 0.0024
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -0.7678 0.1303 34.7133 <.0001
NDRUGTX 1 -0.0749 0.0247 9.2203 0.0024
The LOGISTIC Procedure
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
NDRUGTX 0.928 0.884 0.974
Association of Predicted Probabilities and Observed Responses
Percent Concordant 54.6 Somers' D 0.203
Percent Discordant 34.3 Gamma 0.228
Percent Tied 11.1 Tau-a 0.077
Pairs 62916 c 0.602
proc logistic data=uis41 desc;
model dfree = ivhx2 ivhx3;
run;
The LOGISTIC Procedure
Model Information
Data Set WORK.UIS41
Response Variable DFREE
Number of Response Levels 2
Number of Observations 575
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value DFREE Frequency
1 1 147
2 0 428
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 655.729 646.376
SC 660.083 659.440
-2 Log L 653.729 640.376
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 13.3525 2 0.0013
Score 13.4161 2 0.0012
Wald 13.1585 2 0.0014
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -0.6797 0.1417 22.9977 <.0001
IVHX2 1 -0.4810 0.2657 3.2773 0.0702
IVHX3 1 -0.7748 0.2166 12.7997 0.0003
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
IVHX2 0.618 0.367 1.041
IVHX3 0.461 0.301 0.704
Association of Predicted Probabilities and Observed Responses
Percent Concordant 41.5 Somers' D 0.185
Percent Discordant 23.0 Gamma 0.287
Percent Tied 35.5 Tau-a 0.071
Pairs 62916 c 0.593
proc logistic data=uis41 desc;
model dfree = race;
run;
The LOGISTIC Procedure
Model Information
Data Set WORK.UIS41
Response Variable DFREE
Number of Response Levels 2
Number of Observations 575
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value DFREE Frequency
1 1 147
2 0 428
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 655.729 653.105
SC 660.083 661.814
-2 Log L 653.729 649.105
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 4.6235 1 0.0315
Score 4.7791 1 0.0288
Wald 4.7378 1 0.0295
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.1939 0.1142 109.3946 <.0001
RACE 1 0.4592 0.2110 4.7378 0.0295
The LOGISTIC Procedure
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
RACE 1.583 1.047 2.393
Association of Predicted Probabilities and Observed Responses
Percent Concordant 24.7 Somers' D 0.091
Percent Discordant 15.6 Gamma 0.226
Percent Tied 59.8 Tau-a 0.035
Pairs 62916 c 0.545
proc logistic data=uis41 desc;
model dfree = treat;
run;
The LOGISTIC Procedure
Model Information
Data Set WORK.UIS41
Response Variable DFREE
Number of Response Levels 2
Number of Observations 575
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value DFREE Frequency
1 1 147
2 0 428
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 655.729 652.551
SC 660.083 661.259
-2 Log L 653.729 648.551
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 5.1782 1 0.0229
Score 5.1626 1 0.0231
Wald 5.1266 1 0.0236
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.2978 0.1433 82.0211 <.0001
TREAT 1 0.4371 0.1931 5.1266 0.0236
The LOGISTIC Procedure
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
TREAT 1.548 1.060 2.260
Association of Predicted Probabilities and Observed Responses
Percent Concordant 30.7 Somers' D 0.109
Percent Discordant 19.8 Gamma 0.215
Percent Tied 49.5 Tau-a 0.041
Pairs 62916 c 0.554
proc logistic data=uis41 desc;
model dfree = site;
run;
The LOGISTIC Procedure
Model Information
Data Set WORK.UIS41
Response Variable DFREE
Number of Response Levels 2
Number of Observations 575
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value DFREE Frequency
1 1 147
2 0 428
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 655.729 656.063
SC 660.083 664.772
-2 Log L 653.729 652.063
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 1.6659 1 0.1968
Score 1.6921 1 0.1933
Wald 1.6874 1 0.1939
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.1527 0.1171 96.9397 <.0001
SITE 1 0.2642 0.2034 1.6874 0.1939
The LOGISTIC Procedure
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
SITE 1.302 0.874 1.940
Association of Predicted Probabilities and Observed Responses
Percent Concordant 24.6 Somers' D 0.057
Percent Discordant 18.9 Gamma 0.131
Percent Tied 56.4 Tau-a 0.022
Pairs 62916 c 0.529
page 106 Table 4.2 Results of fitting a multivariable model containing the covariates significant at the 0.25 level in Table 4.1.
proc logistic data=uis41 desc;
model dfree = age ndrugtx ivhx2 ivhx3 race treat site / alpha=.25;
run;
The LOGISTIC Procedure
Model Information
Data Set WORK.UIS41
Response Variable DFREE
Number of Response Levels 2
Number of Observations 575
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value DFREE Frequency
1 1 147
2 0 428
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 655.729 635.248
SC 660.083 670.083
-2 Log L 653.729 619.248
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 34.4806 7 <.0001
Score 32.6795 7 <.0001
Wald 30.6395 7 <.0001
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -2.4054 0.5548 18.7975 <.0001
AGE 1 0.0504 0.0173 8.4550 0.0036
NDRUGTX 1 -0.0615 0.0256 5.7559 0.0164
IVHX2 1 -0.6033 0.2872 4.4118 0.0357
IVHX3 1 -0.7327 0.2523 8.4328 0.0037
RACE 1 0.2261 0.2233 1.0251 0.3113
TREAT 1 0.4425 0.1993 4.9302 0.0264
SITE 1 0.1486 0.2172 0.4681 0.4939
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
AGE 1.052 1.017 1.088
NDRUGTX 0.940 0.894 0.989
IVHX2 0.547 0.312 0.960
IVHX3 0.481 0.293 0.788
RACE 1.254 0.809 1.942
TREAT 1.557 1.053 2.300
SITE 1.160 0.758 1.776
Association of Predicted Probabilities and Observed Responses
Percent Concordant 66.6 Somers' D 0.336
Percent Discordant 33.0 Gamma 0.337
Percent Tied 0.4 Tau-a 0.128
Pairs 62916 c 0.668
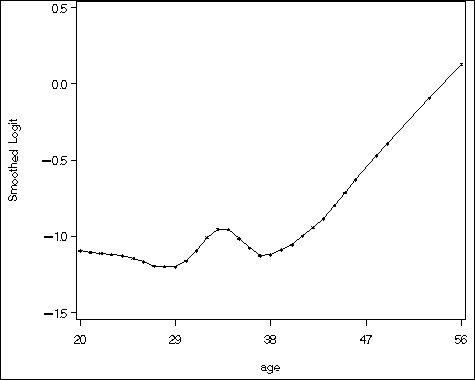
page 107 Figure 4.2 Univariable lowess smoothed logit versus AGE.The smoothing algorithm below is based on Stata's lowess program with logit option. The discrepancy between the two plots by Stata and SAS is due to the difference between the algorithms used by Stata and SAS for Loess smoothing.
proc loess data = uis; model dfree = age /smooth=.6; ods output OutputStatistics=a; run; proc sql; /*compute the total number of obs*/ select count(dfree) into :total from uis; quit; data b1; set a; adjust = 1/&total; small = .0001; if pred < small then pred = adjust; else if pred > 1 - small then pred = 1 - adjust; pred = log(pred/(1-pred)); run; proc sort data = b1; by age; run; goptions reset = all; symbol i = join v=star; axis1 order = (20 to 56 by 9) minor=none; axis2 order = (-1.5 to .5 by .5) minor = none label=(a=90 'Smoothed Logit'); proc gplot data = b1; format age 3.0 pred 5.1; plot pred*age /vaxis=axis2 haxis=axis1 ; run; quit;
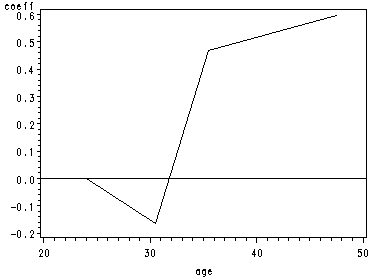
page 107 Table 4.3 Results of the quartile analyses of AGE from the multivariable model containing the variable shown in the model in Table 4.2.
data table4_3;
input quartile midpt number age coeff;
cards;
1 24 148 24 0
2 30.5 144 30.5 -.165864
3 35.5 166 35.5 .4693399
4 47.5 117 47.5 .595771
;
run;
proc print data=table4_3;
run;
Obs quartile midpt number age coeff
1 1 24.0 148 24.0 0.00000
2 2 30.5 144 30.5 -0.16586
3 3 35.5 166 35.5 0.46934
4 4 47.5 117 47.5 0.59577
proc sort data=uis41;
by age;
run;
data uis41a;
set uis41;
age1 = (_n_ <= 148);
age2 = (_n_ >= 149) & (_n_ <= 292);
age3 = (_n_ >= 293) & (_n_ <= 458) ;
age4 = (_n_ >= 459) ;
run;
proc logistic data=uis41a desc;
model dfree = age2 age3 age4 ndrugtx ivhx2 ivhx3 race treat site / CLPARM=both;
run;
The LOGISTIC Procedure
Model Information
Data Set WORK.UIS41A
Response Variable DFREE
Number of Response Levels 2
Number of Observations 575
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value DFREE Frequency
1 1 147
2 0 428
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 655.729 639.042
SC 660.083 682.586
-2 Log L 653.729 619.042
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 34.6869 9 <.0001
Score 32.7145 9 0.0001
Wald 30.6492 9 0.0003
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.0549 0.2706 15.1988 <.0001
age2 1 -0.1659 0.2909 0.3250 0.5686
age3 1 0.4693 0.2707 3.0067 0.0829
age4 1 0.5957 0.3125 3.6344 0.0566
NDRUGTX 1 -0.0587 0.0255 5.3185 0.0211
IVHX2 1 -0.5545 0.2854 3.7764 0.0520
IVHX3 1 -0.6726 0.2519 7.1312 0.0076
RACE 1 0.2787 0.2238 1.5502 0.2131
TREAT 1 0.4431 0.2000 4.9054 0.0268
SITE 1 0.1582 0.2188 0.5228 0.4696
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
age2 0.847 0.479 1.498
age3 1.599 0.941 2.718
age4 1.814 0.983 3.348
NDRUGTX 0.943 0.897 0.991
IVHX2 0.574 0.328 1.005
IVHX3 0.510 0.312 0.836
RACE 1.321 0.852 2.049
TREAT 1.557 1.052 2.305
SITE 1.171 0.763 1.799
Association of Predicted Probabilities and Observed Responses
Percent Concordant 66.2 Somers' D 0.330
Percent Discordant 33.2 Gamma 0.332
Percent Tied 0.7 Tau-a 0.126
Pairs 62916 c 0.665
Profile Likelihood Confidence
Interval for Parameters
Parameter Estimate 95% Confidence Limits
Intercept -1.0549 -1.5955 -0.5327
age2 -0.1659 -0.7410 0.4027
age3 0.4693 -0.0577 1.0054
age4 0.5957 -0.0161 1.2118
NDRUGTX -0.0587 -0.1122 -0.0121
IVHX2 -0.5545 -1.1266 -0.00495
The LOGISTIC Procedure
Profile Likelihood Confidence
Interval for Parameters
Parameter Estimate 95% Confidence Limits
IVHX3 -0.6726 -1.1721 -0.1830
RACE 0.2787 -0.1647 0.7142
TREAT 0.4431 0.0528 0.8380
SITE 0.1582 -0.2747 0.5844
Wald Confidence Interval for Parameters
Parameter Estimate 95% Confidence Limits
Intercept -1.0549 -1.5852 -0.5246
age2 -0.1659 -0.7360 0.4043
age3 0.4693 -0.0612 0.9998
age4 0.5957 -0.0167 1.2082
NDRUGTX -0.0587 -0.1086 -0.00882
IVHX2 -0.5545 -1.1138 0.00476
IVHX3 -0.6726 -1.1662 -0.1789
RACE 0.2787 -0.1600 0.7174
TREAT 0.4431 0.0510 0.8351
SITE 0.1582 -0.2707 0.5871
page 108 Figure 4.3 Plot of estimated logistic regression coefficients versus approximate quartile midpoints of AGE.
symbol1 i=join ; proc gplot data=table4_3; plot coeff*age / vref=0; run; quit;
page 109 Table 4.4 Summary of the use of the method of fractional polynomials for AGE.
NOTE: The values in the column titled deviance are under the heading -2 Log L intercepts and covariates in the SAS output.
data uistbl44; set uis41; agethree=age**3; age_2 = age**(-2); run;
NOTE: Line 1: Not in model
proc logistic data=uistbl44 desc;
model dfree = ndrugtx ivhx2 ivhx3 race treat site;
run;
The LOGISTIC Procedure
Model Information
Data Set WORK.UISTBL44
Response Variable DFREE
Number of Response Levels 2
Number of Observations 575
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value DFREE Frequency
1 1 147
2 0 428
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 655.729 641.801
SC 660.083 672.281
-2 Log L 653.729 627.801
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 25.9282 6 0.0002
Score 24.7124 6 0.0004
Wald 23.3984 6 0.0007
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -0.9462 0.2264 17.4734 <.0001
NDRUGTX 1 -0.0523 0.0246 4.5227 0.0334
IVHX2 1 -0.3853 0.2731 1.9903 0.1583
IVHX3 1 -0.4994 0.2354 4.4990 0.0339
RACE 1 0.2973 0.2205 1.8179 0.1776
TREAT 1 0.4117 0.1974 4.3494 0.0370
SITE 1 0.1784 0.2151 0.6883 0.4067
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
NDRUGTX 0.949 0.904 0.996
IVHX2 0.680 0.398 1.162
IVHX3 0.607 0.383 0.963
RACE 1.346 0.874 2.074
TREAT 1.509 1.025 2.222
SITE 1.195 0.784 1.822
Association of Predicted Probabilities and Observed Responses
Percent Concordant 63.9 Somers' D 0.288
Percent Discordant 35.0 Gamma 0.292
Percent Tied 1.1 Tau-a 0.110
Pairs 62916 c 0.644
NOTE: Line 2: Linear
proc logistic data=uistbl44 desc; model dfree = age ndrugtx ivhx2 ivhx3 race treat site; run;The LOGISTIC Procedure Model Information Data Set WORK.UISTBL44 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 635.248 SC 660.083 670.083 -2 Log L 653.729 619.248 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 34.4806 7 <.0001 Score 32.6795 7 <.0001 Wald 30.6395 7 <.0001 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -2.4054 0.5548 18.7975 <.0001 AGE 1 0.0504 0.0173 8.4550 0.0036 NDRUGTX 1 -0.0615 0.0256 5.7559 0.0164 IVHX2 1 -0.6033 0.2872 4.4118 0.0357 IVHX3 1 -0.7327 0.2523 8.4328 0.0037 RACE 1 0.2261 0.2233 1.0251 0.3113 TREAT 1 0.4425 0.1993 4.9302 0.0264 SITE 1 0.1486 0.2172 0.4681 0.4939 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits AGE 1.052 1.017 1.088 NDRUGTX 0.940 0.894 0.989 IVHX2 0.547 0.312 0.960 IVHX3 0.481 0.293 0.788 RACE 1.254 0.809 1.942 TREAT 1.557 1.053 2.300 SITE 1.160 0.758 1.776 Association of Predicted Probabilities and Observed Responses Percent Concordant 66.6 Somers' D 0.336 Percent Discordant 33.0 Gamma 0.337 Percent Tied 0.4 Tau-a 0.128 Pairs 62916 c 0.668NOTE: Line 3: J = 1proc logistic data=uistbl44 desc; model dfree = agethree ndrugtx ivhx2 ivhx3 race treat site; run; The LOGISTIC Procedure Model Information Data Set WORK.UISTBL44 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 634.882 SC 660.083 669.717 -2 Log L 653.729 618.882 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 34.8466 7 <.0001 Score 33.0920 7 <.0001 Wald 30.8612 7 <.0001 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -1.3032 0.2583 25.4622 <.0001 agethree 1 0.000014 4.648E-6 8.9327 0.0028 NDRUGTX 1 -0.0620 0.0257 5.8134 0.0159 IVHX2 1 -0.5961 0.2869 4.3184 0.0377 IVHX3 1 -0.7142 0.2500 8.1632 0.0043 RACE 1 0.2355 0.2230 1.1152 0.2909 TREAT 1 0.4349 0.1992 4.7634 0.0291 SITE 1 0.1437 0.2174 0.4370 0.5086 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits agethree 1.000 1.000 1.000 NDRUGTX 0.940 0.894 0.988 IVHX2 0.551 0.314 0.967 IVHX3 0.490 0.300 0.799 RACE 1.266 0.817 1.959 TREAT 1.545 1.045 2.283 SITE 1.155 0.754 1.768 Association of Predicted Probabilities and Observed Responses Percent Concordant 66.5 Somers' D 0.335 Percent Discordant 33.0 Gamma 0.337 Percent Tied 0.5 Tau-a 0.128 Pairs 62916 c 0.667G = 619.248 - 618.882 = .366
NOTE: Line 4: J = 2proc logistic data=uistbl44 desc; model dfree = ndrugtx agethree age_2 ivhx2 ivhx3 race treat site; run; The LOGISTIC Procedure Model Information Data Set WORK.UISTBL44 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 636.769 SC 660.083 675.958 -2 Log L 653.729 618.769 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 34.9602 8 <.0001 Score 33.1864 8 <.0001 Wald 31.0132 8 0.0001 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -1.0496 0.7957 1.7401 0.1871 NDRUGTX 1 -0.0620 0.0257 5.8171 0.0159 agethree 1 0.000012 8.098E-6 2.0724 0.1500 age_2 1 -153.9 457.6 0.1131 0.7367 IVHX2 1 -0.6058 0.2882 4.4192 0.0355 IVHX3 1 -0.7264 0.2526 8.2703 0.0040 RACE 1 0.2282 0.2241 1.0371 0.3085 TREAT 1 0.4393 0.1997 4.8384 0.0278 SITE 1 0.1459 0.2175 0.4502 0.5022 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits NDRUGTX 0.940 0.894 0.988 agethree 1.000 1.000 1.000 age_2 <0.001 <0.001 >999.999 IVHX2 0.546 0.310 0.960 IVHX3 0.484 0.295 0.793 RACE 1.256 0.810 1.949 TREAT 1.552 1.049 2.295 SITE 1.157 0.756 1.772 Association of Predicted Probabilities and Observed Responses Percent Concordant 66.6 Somers' D 0.337 Percent Discordant 32.9 Gamma 0.339 Percent Tied 0.5 Tau-a 0.128 Pairs 62916 c 0.668 G = 618.882 - 618.769 = .479
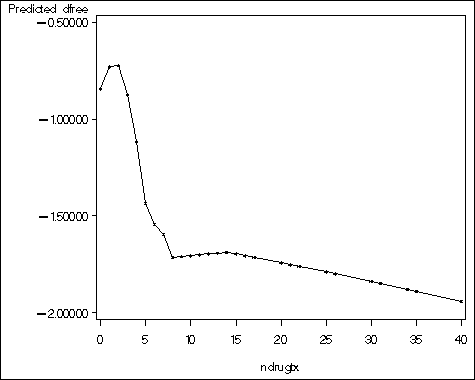
page 110 Figure 4.4 Univariable lowess smoothed logit versus number of previous drug treatments (NDRGTX).
The smoothing algorithm below is based on Stata's lowess program with logit option. The discrepancy between the two plots by Stata and SAS is due to the difference between the algorithms used by Stata and SAS for Loess smoothing.
proc loess data = uis; model dfree = ndrugtx /smooth=.5; ods output OutputStatistics=a; run; proc means data = a; var pred; run; proc sql; /*compute the total number of obs*/ select count(dfree) into :total from uis; quit; data b1; set a; adjust = 1/&total; small = .0001; if pred < small then pred = adjust; else if pred > 1 - small then pred = 1 - adjust; pred = log(pred/(1-pred)); run; proc sort data = b1; by ndrugtx; run; goptions ftext = swiss htitle = 5 htext = 3 gunit = pct border cback = white hsize = 5in vsize = 4in; filename outgraph 'd:temphttps://stats.idre.ucla.edu/wp-content/uploads/2016/02/alr2.gif'; goptions gsfname = outgraph dev = gif570; symbol i = join v=star; axis1 order = (0 to 40 by 5) minor=none; axis2 order = (-2 to -.5 by .5) minor = none; proc gplot data = b1; format ndrugtx 3.0 ; plot pred*ndrugtx /vaxis=axis2 haxis=axis1 ; run; quit;
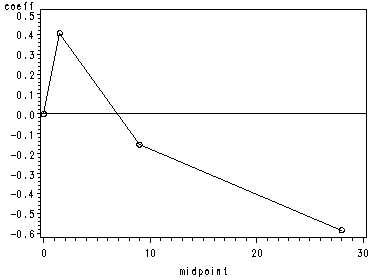
page 110 Table 4.5 Results of the design variable analysis of number of previous drug treatments (NDRGTX) from the multivariable model containing the variables shown in the model in Table 4.2.data uis42; set uis41; grp = .; if ndrugtx=0 then grp = 1; if ndrugtx=1 or ndrugtx=2 then grp = 2; if 3<=ndrugtx<16 then grp = 3; if ndrugtx>15 then grp = 4; if grp = 2 then grp2 = 1; else grp2 = 0; if grp = 3 then grp3 = 1; else grp3 = 0; if grp = 4 then grp4 = 1; else grp4 = 0; run; proc logistic data=uis42 desc; model dfree = age grp2 grp3 grp4 ivhx2 ivhx3 race treat site / CLPARM=both; run; The LOGISTIC Procedure Model Information Data Set WORK.UIS42 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 638.638 SC 660.083 682.182 -2 Log L 653.729 618.638 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 35.0906 9 <.0001 Score 34.5976 9 <.0001 Wald 32.5146 9 0.0002 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -2.6601 0.6060 19.2711 <.0001 AGE 1 0.0506 0.0173 8.5540 0.0034 grp2 1 0.4060 0.3090 1.7262 0.1889 grp3 1 -0.1537 0.3117 0.2432 0.6219 grp4 1 -0.5852 0.6206 0.8894 0.3457 IVHX2 1 -0.6478 0.2898 4.9958 0.0254 IVHX3 1 -0.7955 0.2542 9.7909 0.0018 RACE 1 0.2412 0.2244 1.1551 0.2825 TREAT 1 0.4199 0.1997 4.4230 0.0355 SITE 1 0.1619 0.2206 0.5385 0.4630 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits AGE 1.052 1.017 1.088 grp2 1.501 0.819 2.750 grp3 0.858 0.466 1.580 grp4 0.557 0.165 1.880 IVHX2 0.523 0.296 0.923 IVHX3 0.451 0.274 0.743 RACE 1.273 0.820 1.976 TREAT 1.522 1.029 2.251 SITE 1.176 0.763 1.812 Association of Predicted Probabilities and Observed Responses Percent Concordant 66.2 Somers' D 0.330 Percent Discordant 33.2 Gamma 0.332 Percent Tied 0.6 Tau-a 0.126 Pairs 62916 c 0.665 Profile Likelihood Confidence Interval for Parameters Parameter Estimate 95% Confidence Limits Intercept -2.6601 -3.8671 -1.4871 AGE 0.0506 0.0168 0.0848 grp2 0.4060 -0.1906 1.0244 grp3 -0.1537 -0.7559 0.4696 grp4 -0.5852 -1.9302 0.5550 IVHX2 -0.6478 -1.2289 -0.0898 The LOGISTIC Procedure Profile Likelihood Confidence Interval for Parameters Parameter Estimate 95% Confidence Limits IVHX3 -0.7955 -1.2996 -0.3012 RACE 0.2412 -0.2037 0.6775 TREAT 0.4199 0.0302 0.8140 SITE 0.1619 -0.2745 0.5916 Wald Confidence Interval for Parameters Parameter Estimate 95% Confidence Limits Intercept -2.6601 -3.8477 -1.4724 AGE 0.0506 0.0167 0.0845 grp2 0.4060 -0.1997 1.0117 grp3 -0.1537 -0.7646 0.4572 grp4 -0.5852 -1.8015 0.6311 IVHX2 -0.6478 -1.2158 -0.0797 IVHX3 -0.7955 -1.2938 -0.2972 RACE 0.2412 -0.1987 0.6810 TREAT 0.4199 0.0286 0.8113 SITE 0.1619 -0.2705 0.5943 data table4_4; input group midpoint number coeff; cards; 1 0 79 0 2 1.5 173 .406 3 9 294 -.154 4 28 29 -.585 ; run; proc print data=table4_4; run; Obs group midpoint number coeff 1 1 0.0 79 0.000 2 2 1.5 173 0.406 3 3 9.0 294 -0.154 4 4 28.0 29 -0.585page 111 Figure 4.5 Plot of estimated logistic regression coefficients from Table 4.4 versus the midpoints of number of previous drug treatment groups.symbol1 i=join value=circle; proc gplot data=table4_4; plot coeff*midpoint / vref=0; run; quit;
page 112 Figure 4.6 Plot of the univariable lowess smoothed logit (o) and the multivariable adjusted logit (+) from the J = 2 fractional polynomial model versus number of previous drug treatments (NDRGTX).
NOTE: We were unable to reproduce this graph.
page 113 Table 4.7 Results of fitting the multivariable model with the two term fractional polynomial transformation of NDRGTX.
NOTE: Everything regarding the constant in this output is different from what is shown in the book, and we don't know why.
data uis43; set uis41; ndrgfp1 = ((ndrugtx+1)/10)**(-1); ndrgfp2 = ndrgfp1*log((ndrugtx+1)/10); run; proc logistic data=uis43 desc; model dfree = age ndrgfp1 ndrgfp2 ivhx2 ivhx3 race treat site; run; The LOGISTIC Procedure Model Information Data Set WORK.UIS43 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 631.451 SC 660.083 670.640 -2 Log L 653.729 613.451 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 40.2777 8 <.0001 Score 38.7032 8 <.0001 Wald 36.1456 8 <.0001 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -4.3137 0.7925 29.6321 <.0001 AGE 1 0.0544 0.0175 9.6928 0.0018 ndrgfp1 1 0.9814 0.2888 11.5446 0.0007 ndrgfp2 1 0.3611 0.1099 10.8050 0.0010 IVHX2 1 -0.6088 0.2911 4.3740 0.0365 IVHX3 1 -0.7238 0.2556 8.0213 0.0046 RACE 1 0.2477 0.2242 1.2205 0.2693 TREAT 1 0.4224 0.2004 4.4435 0.0350 SITE 1 0.1732 0.2210 0.6144 0.4331 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits AGE 1.056 1.020 1.093 ndrgfp1 2.668 1.515 4.700 ndrgfp2 1.435 1.157 1.780 IVHX2 0.544 0.307 0.962 IVHX3 0.485 0.294 0.800 RACE 1.281 0.826 1.988 TREAT 1.526 1.030 2.259 SITE 1.189 0.771 1.834 Association of Predicted Probabilities and Observed Responses Percent Concordant 67.2 Somers' D 0.348 Percent Discordant 32.4 Gamma 0.349 Percent Tied 0.5 Tau-a 0.133 Pairs 62916 c 0.674page 115 Table 4.9 Preliminary final model containing significant main effects and interactions.proc logistic data=uis43 desc; model dfree = age ndrgfp1 ndrgfp2 ivhx2 ivhx3 race treat site age*ndrgfp1 race*site; run; The LOGISTIC Procedure Model Information Data Set WORK.UIS43 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 619.963 SC 660.083 667.861 -2 Log L 653.729 597.963 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 55.7660 10 <.0001 Score 52.0723 10 <.0001 Wald 47.2784 10 <.0001 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -6.8429 1.2193 31.4989 <.0001 AGE 1 0.1166 0.0289 16.3137 <.0001 ndrgfp1 1 1.6687 0.4071 16.8000 <.0001 ndrgfp2 1 0.4336 0.1169 13.7585 0.0002 IVHX2 1 -0.6346 0.2987 4.5134 0.0336 IVHX3 1 -0.7049 0.2616 7.2623 0.0070 RACE 1 0.6841 0.2641 6.7074 0.0096 TREAT 1 0.4349 0.2038 4.5559 0.0328 SITE 1 0.5162 0.2549 4.1013 0.0429 AGE*ndrgfp1 1 -0.0153 0.00603 6.4177 0.0113 RACE*SITE 1 -1.4294 0.5298 7.2799 0.0070 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits ndrgfp2 1.543 1.227 1.940 IVHX2 0.530 0.295 0.952 IVHX3 0.494 0.296 0.825 TREAT 1.545 1.036 2.303 Association of Predicted Probabilities and Observed Responses Percent Concordant 69.7 Somers' D 0.398 Percent Discordant 29.9 Gamma 0.399 Percent Tied 0.4 Tau-a 0.152 Pairs 62916 c 0.6994.3 Stepwise logistic regression
page 123 Table 4.11 Log-likelihood for the model at each step and likelihood ratio test statistics (G), degrees-of-freedom (df), and p-values for two methods of selecting variables for a final model from a summary table.
NOTE: The following code gives the log likelihood and the values for method 1.proc logistic data=uis43 desc; model dfree = ; run; The LOGISTIC Procedure Model Information Data Set WORK.UIS43 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. -2 Log L = 653.7289 Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -1.0687 0.0956 124.9675 <.0001 proc logistic data=uis43 desc; model dfree = ndrugtx; run; The LOGISTIC Procedure Model Information Data Set WORK.UIS43 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 645.890 SC 660.083 654.598 -2 Log L 653.729 641.890 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 11.8392 1 0.0006 Score 9.7585 1 0.0018 Wald 9.2203 1 0.0024 Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -0.7678 0.1303 34.7133 <.0001 NDRUGTX 1 -0.0749 0.0247 9.2203 0.0024 The LOGISTIC Procedure Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits NDRUGTX 0.928 0.884 0.974 Association of Predicted Probabilities and Observed Responses Percent Concordant 54.6 Somers' D 0.203 Percent Discordant 34.3 Gamma 0.228 Percent Tied 11.1 Tau-a 0.077 Pairs 62916 c 0.602NOTE: To get the value of G, you need to compare the two models by doing some calculations by hand:
-2*(-326.864-(-320.945)) = 11.84proc logistic data=uis43 desc; model dfree = ndrugtx treat; run; The LOGISTIC Procedure Model Information Data Set WORK.UIS43 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 642.860 SC 660.083 655.923 -2 Log L 653.729 636.860 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 16.8690 2 0.0002 Score 14.8924 2 0.0006 Wald 14.2225 2 0.0008 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -0.9991 0.1691 34.9214 <.0001 NDRUGTX 1 -0.0739 0.0245 9.1221 0.0025 TREAT 1 0.4348 0.1948 4.9830 0.0256 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits NDRUGTX 0.929 0.885 0.974 TREAT 1.545 1.054 2.263 Association of Predicted Probabilities and Observed Responses Percent Concordant 58.8 Somers' D 0.232 Percent Discordant 35.5 Gamma 0.246 Percent Tied 5.7 Tau-a 0.089 Pairs 62916 c 0.616-2*(-320.945-(-318.430)) = 5.03proc logistic data=uis43 desc; model dfree = ndrugtx treat ivhx2 ivhx3; run; The LOGISTIC Procedure Model Information Data Set WORK.UIS43 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 640.050 SC 660.083 661.822 -2 Log L 653.729 630.050 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 23.6784 4 <.0001 Score 22.3908 4 0.0002 Wald 21.3059 4 0.0003 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -0.7714 0.1878 16.8787 <.0001 NDRUGTX 1 -0.0542 0.0246 4.8559 0.0276 TREAT 1 0.4215 0.1965 4.6009 0.0320 IVHX2 1 -0.4024 0.2711 2.2040 0.1377 IVHX3 1 -0.5804 0.2289 6.4281 0.0112 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits NDRUGTX 0.947 0.903 0.994 TREAT 1.524 1.037 2.241 IVHX2 0.669 0.393 1.138 IVHX3 0.560 0.357 0.877 Association of Predicted Probabilities and Observed Responses Percent Concordant 62.2 Somers' D 0.269 Percent Discordant 35.3 Gamma 0.276 Percent Tied 2.5 Tau-a 0.103 Pairs 62916 c 0.635-2*(-318.430-(-315.025)) = 6.81proc logistic data=uis43 desc; model dfree = ndrugtx treat ivhx2 ivhx3 age ; run; The LOGISTIC Procedure Model Information Data Set WORK.UIS43 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 632.587 SC 660.083 658.713 -2 Log L 653.729 620.587 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 33.1420 5 <.0001 Score 31.1565 5 <.0001 Wald 29.3324 5 <.0001 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -2.3327 0.5484 18.0956 <.0001 NDRUGTX 1 -0.0637 0.0256 6.1858 0.0129 TREAT 1 0.4513 0.1986 5.1649 0.0230 IVHX2 1 -0.6237 0.2847 4.7989 0.0285 IVHX3 1 -0.8056 0.2445 10.8542 0.0010 AGE 1 0.0526 0.0172 9.3378 0.0022 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits NDRUGTX 0.938 0.892 0.987 TREAT 1.570 1.064 2.318 IVHX2 0.536 0.307 0.936 IVHX3 0.447 0.277 0.722 AGE 1.054 1.019 1.090 Association of Predicted Probabilities and Observed Responses Percent Concordant 65.5 Somers' D 0.315 Percent Discordant 34.0 Gamma 0.317 Percent Tied 0.5 Tau-a 0.120 Pairs 62916 c 0.658-2*(-315.025-(-310.293)) = 9.46
NOTE: The following code gives the log likelihood and the values for method 2.
-2*(-326.864-(-310.293)) = 33.14
-2*(-320.945-(-310.293)) = 21.30
-2*(-318.430-(-310.293)) = 16.27
-2*(-315.025-(-310.293)) = 9.46
page 126 Table 4.12 Results of applying stepwise variable selection using the score test to select and maximum likelihood test to remove covariates at each step to the UIS data. Results are presented at each step in terms of the p-values to enter (below the horizontal line), and the p-value to remove (above the horizontal line) in each column. The asterisk denotes the maximum p-value to remove at each step.proc logistic data=uis43 desc; class ivhx; model dfree = ivhx age ndrugtx treat race site beck / selection=stepwise slentry=0.15 slstay=0.20 details; run; The LOGISTIC Procedure Model Information Data Set WORK.UIS43 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Stepwise Selection Procedure Class Level Information Design Variables Class Value 1 2 IVHX 1 1 0 2 0 1 3 -1 -1 Step 0. Intercept entered: Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr ChiSq Intercept 1 -1.0687 0.0956 124.9675 .0001 The LOGISTIC Procedure Residual Chi-Square Test Chi-Square DF Pr ChiSq 32.6798 8 .0001 Analysis of Effects Not in the Model Score Effect DF Chi-Square Pr ChiSq IVHX 2 13.4161 0.0012 AGE 1 1.4063 0.2357 NDRUGTX 1 9.7585 0.0018 TREAT 1 5.1626 0.0231 RACE 1 4.7791 0.0288 SITE 1 1.6921 0.1933 BECK 1 0.6331 0.4262 Step 1. Effect IVHX entered: Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 646.376 SC 660.083 659.440 -2 Log L 653.729 640.376 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 13.3525 2 0.0013 Score 13.4161 2 0.0012 Wald 13.1585 2 0.0014 The LOGISTIC Procedure Type III Analysis of Effects Wald Effect DF Chi-Square Pr > ChiSq IVHX 2 13.1585 0.0014 Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -1.0983 0.1040 111.4532 <.0001 IVHX 1 1 0.4186 0.1324 10.0021 0.0016 IVHX 2 1 -0.0624 0.1663 0.1408 0.7075 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits IVHX 1 vs 3 2.170 1.420 3.318 IVHX 2 vs 3 1.342 0.778 2.314 Association of Predicted Probabilities and Observed Responses Percent Concordant 41.5 Somers' D 0.185 Percent Discordant 23.0 Gamma 0.287 Percent Tied 35.5 Tau-a 0.071 Pairs 62916 c 0.593 Residual Chi-Square Test Chi-Square DF Pr > ChiSq 20.1460 6 0.0026 Analysis of Effects in Model Wald Effect DF Chi-Square Pr > ChiSq IVHX 2 13.1585 0.0014 The LOGISTIC Procedure Analysis of Effects Not in the Model Score Effect DF Chi-Square Pr > ChiSq AGE 1 7.3328 0.0068 NDRUGTX 1 4.9318 0.0264 TREAT 1 4.5504 0.0329 RACE 1 2.1112 0.1462 SITE 1 0.5585 0.4549 BECK 1 0.0824 0.7741 Step 2. Effect AGE entered: Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 641.096 SC 660.083 658.514 -2 Log L 653.729 633.096 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 20.6325 3 0.0001 Score 20.4581 3 0.0001 Wald 19.7426 3 0.0002 Type III Analysis of Effects Wald Effect DF Chi-Square Pr > ChiSq IVHX 2 18.6217 <.0001 AGE 1 7.2173 0.0072 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -2.5942 0.5727 20.5193 <.0001 IVHX 1 1 0.5610 0.1446 15.0424 0.0001 IVHX 2 1 -0.1200 0.1691 0.5037 0.4779 AGE 1 0.0454 0.0169 7.2173 0.0072 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits IVHX 1 vs 3 2.724 1.716 4.322 IVHX 2 vs 3 1.378 0.796 2.388 AGE 1.046 1.012 1.082 Association of Predicted Probabilities and Observed Responses Percent Concordant 60.7 Somers' D 0.239 Percent Discordant 36.8 Gamma 0.245 Percent Tied 2.5 Tau-a 0.091 Pairs 62916 c 0.620 Residual Chi-Square Test Chi-Square DF Pr > ChiSq 12.8529 5 0.0248 Analysis of Effects in Model Wald Effect DF Chi-Square Pr > ChiSq IVHX 2 18.6217 <.0001 AGE 1 7.2173 0.0072 Analysis of Effects Not in the Model Score Effect DF Chi-Square Pr > ChiSq NDRUGTX 1 6.2094 0.0127 TREAT 1 5.0083 0.0252 RACE 1 1.4228 0.2330 SITE 1 0.5078 0.4761 BECK 1 0.0021 0.9636 Step 3. Effect NDRUGTX entered: Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 635.805 SC 660.083 657.577 -2 Log L 653.729 625.805 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 27.9241 4 <.0001 Score 26.1214 4 <.0001 Wald 24.7400 4 <.0001 Type III Analysis of Effects Wald Effect DF Chi-Square Pr > ChiSq IVHX 2 11.8349 0.0027 AGE 1 8.7808 0.0030 NDRUGTX 1 6.0226 0.0141 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -2.5107 0.5759 19.0072 <.0001 IVHX 1 1 0.4699 0.1484 10.0285 0.0015 IVHX 2 1 -0.1201 0.1705 0.4958 0.4813 AGE 1 0.0508 0.0171 8.7808 0.0030 NDRUGTX 1 -0.0632 0.0258 6.0226 0.0141 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits IVHX 1 vs 3 2.270 1.408 3.659 IVHX 2 vs 3 1.258 0.721 2.195 AGE 1.052 1.017 1.088 NDRUGTX 0.939 0.893 0.987 Association of Predicted Probabilities and Observed Responses Percent Concordant 64.2 Somers' D 0.291 Percent Discordant 35.1 Gamma 0.293 Percent Tied 0.7 Tau-a 0.111 Pairs 62916 c 0.646 Residual Chi-Square Test Chi-Square DF Pr > ChiSq 6.5523 4 0.1615 Analysis of Effects in Model Wald Effect DF Chi-Square Pr > ChiSq IVHX 2 11.8349 0.0027 AGE 1 8.7808 0.0030 NDRUGTX 1 6.0226 0.0141 The LOGISTIC Procedure Analysis of Effects Not in the Model Score Effect DF Chi-Square Pr > ChiSq TREAT 1 5.2017 0.0226 RACE 1 1.2039 0.2726 SITE 1 0.2416 0.6231 BECK 1 0.0011 0.9738Step 4. Effect TREAT entered: Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 632.587 SC 660.083 658.713 -2 Log L 653.729 620.587 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 33.1420 5 <.0001 Score 31.1565 5 <.0001 Wald 29.3324 5 <.0001 Type III Analysis of Effects Wald Effect DF Chi-Square Pr > ChiSq IVHX 2 11.6227 0.0030 AGE 1 9.3378 0.0022 NDRUGTX 1 6.1858 0.0129 TREAT 1 5.1649 0.0230 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -2.8092 0.5944 22.3362 <.0001 IVHX 1 1 0.4764 0.1490 10.2209 0.0014 IVHX 2 1 -0.1472 0.1719 0.7336 0.3917 AGE 1 0.0526 0.0172 9.3378 0.0022 NDRUGTX 1 -0.0637 0.0256 6.1858 0.0129 TREAT 1 0.4513 0.1986 5.1649 0.0230 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits IVHX 1 vs 3 2.238 1.386 3.614 IVHX 2 vs 3 1.200 0.685 2.101 AGE 1.054 1.019 1.090 NDRUGTX 0.938 0.892 0.987 TREAT 1.570 1.064 2.318 Association of Predicted Probabilities and Observed Responses Percent Concordant 65.5 Somers' D 0.315 Percent Discordant 34.0 Gamma 0.317 Percent Tied 0.5 Tau-a 0.120 Pairs 62916 c 0.658 Residual Chi-Square Test Chi-Square DF Pr > ChiSq 1.3495 3 0.7174 Analysis of Effects in Model Wald Effect DF Chi-Square Pr > ChiSq IVHX 2 11.6227 0.0030 AGE 1 9.3378 0.0022 NDRUGTX 1 6.1858 0.0129 TREAT 1 5.1649 0.0230 The LOGISTIC Procedure Analysis of Effects Not in the Model Score Effect DF Chi-Square Pr > ChiSq RACE 1 0.8844 0.3470 SITE 1 0.3266 0.5676 BECK 1 0.0000 0.9948NOTE: No (additional) effects met the 0.15 significance level for entry into the model. Summary of Stepwise Selection Effect Number Score Wald Step Entered Removed DF In Chi-Square Chi-Square Pr > ChiSq 1 IVHX 2 1 13.4161 . 0.0012 2 AGE 1 2 7.3328 . 0.0068 3 NDRUGTX 1 3 6.2094 . 0.0127 4 TREAT 1 4 5.2017 . 0.0226page 127 Table 4.13 Results of applying stepwise variable selection to interactions from the main effects model from the UIS data, using the maximum likelihood method presented at each step in terms of the p-values to enter (below the horizontal line), and the p-value to remove (above the horizontal line) in each column. The asterisk denotes the maximum p-value to remove at each step.
NOTE: We could not reproduce this table.4.4 Best subsets logistic regression
page 133 Table 4.14 Five best models identified using Mallow's Cq. Model covariates, Mallow's Cq, the Wald test and the likelihood ratio test for the excluded covariates, degrees-of-freedom and p-value.
NOTE: To get the values for Mallow's Cq, you have to use the formula on page 131. To get the values of Wald test and the likelihood ratio test, you need to subtract the values of these tests obtained from the reduced model from the values obtained from the full model. Full model that will be used for comparison:proc logistic data=uis43 desc; model dfree = age beck ndrugtx ivhx2 ivhx3 ndrugtx race treat site / clparm=wald; run; The LOGISTIC Procedure Model Information Data Set WORK.UIS43 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 637.248 SC 660.083 676.437 -2 Log L 653.729 619.248 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 34.4813 8 <.0001 Score 32.6798 8 <.0001 Wald 30.6373 8 0.0002 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -2.4111 0.5983 16.2382 <.0001 AGE 1 0.0504 0.0174 8.3886 0.0038 BECK 1 0.000276 0.0108 0.0007 0.9796 NDRUGTX 1 -0.0615 0.0256 5.7532 0.0165 IVHX2 1 -0.6037 0.2876 4.4065 0.0358 IVHX3 1 -0.7337 0.2550 8.2788 0.0040 RACE 1 0.2260 0.2234 1.0239 0.3116 TREAT 1 0.4425 0.1993 4.9296 0.0264 SITE 1 0.1489 0.2176 0.4685 0.4937 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits AGE 1.052 1.016 1.088 BECK 1.000 0.979 1.022 NDRUGTX 0.940 0.894 0.989 IVHX2 0.547 0.311 0.961 IVHX3 0.480 0.291 0.791 RACE 1.254 0.809 1.942 TREAT 1.557 1.053 2.300 SITE 1.161 0.758 1.778 Association of Predicted Probabilities and Observed Responses Percent Concordant 66.6 Somers' D 0.336 Percent Discordant 33.0 Gamma 0.337 Percent Tied 0.4 Tau-a 0.128 Pairs 62916 c 0.668 Wald Confidence Interval for Parameters Parameter Estimate 95% Confidence Limits Intercept -2.4111 -3.5838 -1.2384 AGE 0.0504 0.0163 0.0845 BECK 0.000276 -0.0209 0.0214 NDRUGTX -0.0615 -0.1118 -0.0112 IVHX2 -0.6037 -1.1674 -0.0400 IVHX3 -0.7337 -1.2334 -0.2339 RACE 0.2260 -0.2118 0.6638 TREAT 0.4425 0.0519 0.8331 SITE 0.1489 -0.2776 0.5754MODEL 1:proc logistic data=uis43 desc; model dfree = age ndrugtx ivhx2 ivhx3 treat / clparm=wald; run; The LOGISTIC Procedure Model Information Data Set WORK.UIS43 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 632.587 SC 660.083 658.713 -2 Log L 653.729 620.587 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 33.1420 5 <.0001 Score 31.1565 5 <.0001 Wald 29.3324 5 <.0001 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -2.3327 0.5484 18.0956 <.0001 AGE 1 0.0526 0.0172 9.3378 0.0022 NDRUGTX 1 -0.0637 0.0256 6.1858 0.0129 IVHX2 1 -0.6237 0.2847 4.7989 0.0285 IVHX3 1 -0.8056 0.2445 10.8542 0.0010 TREAT 1 0.4513 0.1986 5.1649 0.0230 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits AGE 1.054 1.019 1.090 NDRUGTX 0.938 0.892 0.987 IVHX2 0.536 0.307 0.936 IVHX3 0.447 0.277 0.722 TREAT 1.570 1.064 2.318 Association of Predicted Probabilities and Observed Responses Percent Concordant 65.5 Somers' D 0.315 Percent Discordant 34.0 Gamma 0.317 Percent Tied 0.5 Tau-a 0.120 Pairs 62916 c 0.658 Wald Confidence Interval for Parameters Parameter Estimate 95% Confidence Limits Intercept -2.3327 -3.4075 -1.2579 AGE 0.0526 0.0189 0.0863 NDRUGTX -0.0637 -0.1140 -0.0135 IVHX2 -0.6237 -1.1817 -0.0657 IVHX3 -0.8056 -1.2849 -0.3264 TREAT 0.4513 0.0621 0.8406MODEL 2:proc logistic data=uis43 desc; model dfree = age ndrugtx ivhx2 ivhx3 treat race / clparm=wald; run; The LOGISTIC Procedure Model Information Data Set WORK.UIS43 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 633.713 SC 660.083 664.194 -2 Log L 653.729 619.713 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 34.0155 6 <.0001 Score 32.0446 6 <.0001 Wald 30.1184 6 <.0001 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -2.3558 0.5501 18.3394 <.0001 AGE 1 0.0510 0.0173 8.6675 0.0032 NDRUGTX 1 -0.0632 0.0256 6.0657 0.0138 IVHX2 1 -0.5929 0.2864 4.2846 0.0385 IVHX3 1 -0.7601 0.2490 9.3182 0.0023 TREAT 1 0.4390 0.1991 4.8588 0.0275 RACE 1 0.2081 0.2215 0.8831 0.3474 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits AGE 1.052 1.017 1.089 NDRUGTX 0.939 0.893 0.987 IVHX2 0.553 0.315 0.969 IVHX3 0.468 0.287 0.762 TREAT 1.551 1.050 2.292 RACE 1.231 0.798 1.901 Association of Predicted Probabilities and Observed Responses Percent Concordant 66.3 Somers' D 0.331 Percent Discordant 33.2 Gamma 0.332 Percent Tied 0.5 Tau-a 0.126 Pairs 62916 c 0.665 Wald Confidence Interval for Parameters Parameter Estimate 95% Confidence Limits Intercept -2.3558 -3.4339 -1.2776 AGE 0.0510 0.0170 0.0849 NDRUGTX -0.0632 -0.1134 -0.0129 IVHX2 -0.5929 -1.1543 -0.0315 IVHX3 -0.7601 -1.2481 -0.2721 TREAT 0.4390 0.0486 0.8293 RACE 0.2081 -0.2259 0.6421MODEL 3:proc logistic data=uis43 desc; model dfree = age ndrugtx ivhx2 ivhx3 treat site / clparm=wald; run; The LOGISTIC Procedure Model Information Data Set WORK.UIS43 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 634.262 SC 660.083 664.743 -2 Log L 653.729 620.262 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 33.4668 6 <.0001 Score 31.6135 6 <.0001 Wald 29.7216 6 <.0001 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -2.3726 0.5526 18.4307 <.0001 AGE 1 0.0522 0.0172 9.2074 0.0024 NDRUGTX 1 -0.0624 0.0256 5.9312 0.0149 IVHX2 1 -0.6350 0.2857 4.9402 0.0262 IVHX3 1 -0.7860 0.2471 10.1210 0.0015 TREAT 1 0.4553 0.1988 5.2475 0.0220 SITE 1 0.1231 0.2155 0.3266 0.5677 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits AGE 1.054 1.019 1.090 NDRUGTX 0.940 0.894 0.988 IVHX2 0.530 0.303 0.928 IVHX3 0.456 0.281 0.740 TREAT 1.577 1.068 2.328 SITE 1.131 0.741 1.725 Association of Predicted Probabilities and Observed Responses Percent Concordant 65.5 Somers' D 0.316 Percent Discordant 33.9 Gamma 0.318 Percent Tied 0.6 Tau-a 0.120 Pairs 62916 c 0.658 Wald Confidence Interval for Parameters Parameter Estimate 95% Confidence Limits Intercept -2.3726 -3.4557 -1.2894 AGE 0.0522 0.0185 0.0860 NDRUGTX -0.0624 -0.1126 -0.0122 IVHX2 -0.6350 -1.1950 -0.0751 IVHX3 -0.7860 -1.2703 -0.3018 TREAT 0.4553 0.0657 0.8449 SITE 0.1231 -0.2992 0.5455MODEL 4:proc logistic data=uis43 desc; model dfree = age ndrugtx ivhx2 ivhx3 treat beck / clparm=wald; run; The LOGISTIC Procedure Model Information Data Set WORK.UIS43 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 634.587 SC 660.083 665.067 -2 Log L 653.729 620.587 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 33.1421 6 <.0001 Score 31.1569 6 <.0001 Wald 29.3319 6 <.0001 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -2.3341 0.5899 15.6553 <.0001 AGE 1 0.0526 0.0173 9.2555 0.0023 NDRUGTX 1 -0.0637 0.0256 6.1797 0.0129 IVHX2 1 -0.6238 0.2850 4.7908 0.0286 IVHX3 1 -0.8059 0.2474 10.6091 0.0011 TREAT 1 0.4513 0.1986 5.1639 0.0231 BECK 1 0.000069 0.0107 0.0000 0.9949 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits AGE 1.054 1.019 1.090 NDRUGTX 0.938 0.892 0.987 IVHX2 0.536 0.307 0.937 IVHX3 0.447 0.275 0.725 TREAT 1.570 1.064 2.318 BECK 1.000 0.979 1.021 Association of Predicted Probabilities and Observed Responses Percent Concordant 65.5 Somers' D 0.315 Percent Discordant 34.0 Gamma 0.317 Percent Tied 0.5 Tau-a 0.120 Pairs 62916 c 0.658 Wald Confidence Interval for Parameters Parameter Estimate 95% Confidence Limits Intercept -2.3341 -3.4904 -1.1779 AGE 0.0526 0.0187 0.0865 NDRUGTX -0.0637 -0.1140 -0.0135 IVHX2 -0.6238 -1.1823 -0.0652 IVHX3 -0.8059 -1.2908 -0.3209 TREAT 0.4513 0.0621 0.8406 BECK 0.000069 -0.0210 0.0211MODEL 5:proc logistic data=uis43 desc; model dfree = age ndrugtx ivhx3 treat / clparm=wald; run; The LOGISTIC Procedure Model Information Data Set WORK.UIS43 Response Variable DFREE Number of Response Levels 2 Number of Observations 575 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value DFREE Frequency 1 1 147 2 0 428 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 655.729 635.589 SC 660.083 657.360 -2 Log L 653.729 625.589 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 28.1403 4 <.0001 Score 25.9623 4 <.0001 Wald 24.4765 4 <.0001 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -2.1771 0.5402 16.2432 <.0001 AGE 1 0.0425 0.0165 6.6831 0.0097 NDRUGTX 1 -0.0703 0.0259 7.3820 0.0066 IVHX3 1 -0.5641 0.2186 6.6618 0.0098 TREAT 1 0.4276 0.1972 4.6995 0.0302 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits AGE 1.043 1.010 1.078 NDRUGTX 0.932 0.886 0.981 IVHX3 0.569 0.371 0.873 TREAT 1.534 1.042 2.257 Association of Predicted Probabilities and Observed Responses Percent Concordant 64.2 Somers' D 0.290 Percent Discordant 35.2 Gamma 0.292 Percent Tied 0.7 Tau-a 0.111 Pairs 62916 c 0.645 Wald Confidence Interval for Parameters Parameter Estimate 95% Confidence Limits Intercept -2.1771 -3.2358 -1.1184 AGE 0.0425 0.0103 0.0748 NDRUGTX -0.0703 -0.1210 -0.0196 IVHX3 -0.5641 -0.9925 -0.1357 TREAT 0.4276 0.0410 0.8142page 134 Table 4.15 Five best models identified using the score test approximation to Mallow's Cq, (S8 = 32.6798).
NOTE: We were unable to recreate this table.4.5 Numerical problems
page 137 Table 4.16 A contingency table with a zero cell count and the results of fitting a logistic regression model to this data.data hypothet4; input y x cnt; cards; 1 1 7 1 2 12 1 3 20 0 1 13 0 2 8 0 3 0 ; run; proc freq data=hypothet4; tables x*y ; weight cnt; run; The FREQ Procedure Table of x by y x y Frequency| Percent | Row Pct | Col Pct | 0| 1| Total ---------+--------+--------+ 1 | 13 | 7 | 20 | 21.67 | 11.67 | 33.33 | 65.00 | 35.00 | | 61.90 | 17.95 | ---------+--------+--------+ 2 | 8 | 12 | 20 | 13.33 | 20.00 | 33.33 | 40.00 | 60.00 | | 38.10 | 30.77 | ---------+--------+--------+ 3 | 0 | 20 | 20 | 0.00 | 33.33 | 33.33 | 0.00 | 100.00 | | 0.00 | 51.28 | ---------+--------+--------+ Total 21 39 60 35.00 65.00 100.00proc logistic data=hypothet4 desc; class x / PARAM=ref REF=first; model y = x; weight cnt; run;The LOGISTIC Procedure Model Information Data Set WORK.HYPOTHET4 Response Variable y Number of Response Levels 2 Number of Observations 5 Weight Variable cnt Sum of Weights 60 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Total Value y Frequency Weight 1 1 3 39.000000 2 0 2 21.000000 NOTE: 1 observation having zero frequency or weight was excluded since it does not contribute to the analysis. Class Level Information Design Variables Class Value 1 2 x 1 0 0 2 1 0 3 0 1 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 79.694 58.818 SC 79.303 57.647 -2 Log L 77.694 52.818 The LOGISTIC Procedure Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 24.8753 2 <.0001 Score 18.9011 2 <.0001 Wald 2.4518 2 0.2935 Type III Analysis of Effects Wald Effect DF Chi-Square Pr > ChiSq x 2 2.4518 0.2935 Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -0.6190 0.4688 1.7436 0.1867 x 2 1 1.0245 0.6543 2.4517 0.1174 x 3 1 18.9512 2139.2 0.0001 0.9929 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits x 2 vs 1 2.786 0.773 10.043 x 3 vs 1 >999.999 <0.001 >999.999 Association of Predicted Probabilities and Observed Responses Percent Concordant 50.0 Somers' D 0.333 Percent Discordant 16.7 Gamma 0.500 Percent Tied 33.3 Tau-a 0.200 Pairs 6 c 0.667
page 137 Table 4.17 Stratified 2 by 2 contingency tables with a zero cell count within one stratum.
data hypothet41; input z x y cnt; cards; 1 1 1 5 1 1 0 5 1 0 1 2 1 0 0 8 2 1 1 10 2 1 0 2 2 0 1 2 2 0 0 6 3 1 1 15 3 0 1 1 3 0 0 4 ; run; proc freq data=hypothet41; tables z*y*x ; weight cnt; run; The FREQ Procedure Table 1 of y by x Controlling for z=1 y x Frequency| Percent | Row Pct | Col Pct | 0| 1| Total ---------+--------+--------+ 0 | 8 | 5 | 13 | 40.00 | 25.00 | 65.00 | 61.54 | 38.46 | | 80.00 | 50.00 | ---------+--------+--------+ 1 | 2 | 5 | 7 | 10.00 | 25.00 | 35.00 | 28.57 | 71.43 | | 20.00 | 50.00 | ---------+--------+--------+ Total 10 10 20 50.00 50.00 100.00 Table 2 of y by x Controlling for z=2 y x Frequency| Percent | Row Pct | Col Pct | 0| 1| Total ---------+--------+--------+ 0 | 6 | 2 | 8 | 30.00 | 10.00 | 40.00 | 75.00 | 25.00 | | 75.00 | 16.67 | ---------+--------+--------+ 1 | 2 | 10 | 12 | 10.00 | 50.00 | 60.00 | 16.67 | 83.33 | | 25.00 | 83.33 | ---------+--------+--------+ Total 8 12 20 40.00 60.00 100.00 The FREQ Procedure Table 3 of y by x Controlling for z=3 y x Frequency| Percent | Row Pct | Col Pct | 0| 1| Total ---------+--------+--------+ 0 | 4 | 0 | 4 | 20.00 | 0.00 | 20.00 | 100.00 | 0.00 | | 80.00 | 0.00 | ---------+--------+--------+ 1 | 1 | 15 | 16 | 5.00 | 75.00 | 80.00 | 6.25 | 93.75 | | 20.00 | 100.00 | ---------+--------+--------+ Total 5 15 20 25.00 75.00 100.00
page 138 Table 4.18 Results of fitting logistic regression models to the data in Table 4.17.
model 1:
proc logistic data=hypothet41 desc; class x z / PARAM=ref REF=first; model y = x z ; weight cnt; run; The LOGISTIC Procedure Model Information Data Set WORK.HYPOTHET41 Response Variable y Number of Response Levels 2 Number of Observations 11 Weight Variable cnt Sum of Weights 60 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Total Value y Frequency Weight 1 1 6 35.000000 2 0 5 25.000000 Class Level Information Design Variables Class Value 1 2 x 0 0 1 1 z 1 0 0 2 1 0 3 0 1 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 83.503 61.912 SC 83.901 63.504 -2 Log L 81.503 53.912 The LOGISTIC Procedure Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 27.5909 3 <.0001 Score 24.5465 3 <.0001 Wald 17.0901 3 0.0007 Type III Analysis of Effects Wald Effect DF Chi-Square Pr > ChiSq x 1 14.9590 0.0001 z 2 5.4333 0.0661 Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -2.3189 0.7728 9.0050 0.0027 x 1 1 2.7681 0.7157 14.9590 0.0001 z 2 1 1.1888 0.8119 2.1440 0.1431 z 3 1 2.0381 0.8890 5.2563 0.0219 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits x 1 vs 0 15.928 3.917 64.767 z 2 vs 1 3.283 0.669 16.119 z 3 vs 1 7.676 1.344 43.839 Association of Predicted Probabilities and Observed Responses Percent Concordant 50.0 Somers' D 0.167 Percent Discordant 33.3 Gamma 0.200 Percent Tied 16.7 Tau-a 0.091 Pairs 30 c 0.583model 2:
proc logistic data=hypothet41 desc; class x z / PARAM=ref REF=first; model y = x z x*z; weight cnt; run; The LOGISTIC Procedure Model Information Data Set WORK.HYPOTHET41 Response Variable y Number of Response Levels 2 Number of Observations 11 Weight Variable cnt Sum of Weights 60 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Total Value y Frequency Weight 1 1 6 35.000000 2 0 5 25.000000 Class Level Information Design Variables Class Value 1 2 x 0 0 1 1 z 1 0 0 2 1 0 3 0 1 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 83.503 60.686 SC 83.901 63.073 -2 Log L 81.503 48.686 The LOGISTIC Procedure Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 32.8173 5 <.0001 Score 26.8114 5 <.0001 Wald 10.0884 5 0.0728 Type III Analysis of Effects Wald Effect DF Chi-Square Pr > ChiSq x 1 1.8749 0.1709 z 2 0.0764 0.9625 x*z 2 0.7624 0.6830 Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -1.3863 0.7906 3.0749 0.0795 x 1 1 1.3863 1.0124 1.8749 0.1709 z 2 1 0.2877 1.1365 0.0641 0.8002 z 3 1 8.89E-17 1.3693 0.0000 1.0000 x*z 1 2 1 1.3218 1.5138 0.7623 0.3826 x*z 1 3 1 18.2441 2363.8 0.0001 0.9938 Association of Predicted Probabilities and Observed Responses Percent Concordant 46.7 Somers' D 0.167 Percent Discordant 30.0 Gamma 0.217 Percent Tied 23.3 Tau-a 0.091 Pairs 30 c 0.583_IzXx_3~=0 predicts success perfectly. _IzXx_3 is dropped and 15 obs not used. Because of the numerical problem
with the empty cell, you need to use log-exact or stat-exact.
page 139 Table 4.19 Estimated slope, constant, and estimated standard errors when the data have complete separation, quasicomplete separation, and overlap.
data hypothet43; input x y; x1 = x; x2 = x; x3 = x; x4 = x; x5 = x; x6 = x; if _N_ = 6 then x1 = 6; if _N_ = 6 then x2 = 6.05; if _N_ = 6 then x3 = 6.1; if _N_ = 6 then x4 = 6.15; if _N_ = 6 then x5 = 6.2; if _N_ = 6 then x6 = 8; cards; 1 0 2 0 3 0 4 0 5 0 5.5 0 6 1 7 1 8 1 9 1 10 1 11 1 ; run; proc logistic data=hypothet43 desc; model y = x; run;The LOGISTIC Procedure Model Information Data Set WORK.HYPOTHET43 Response Variable y Number of Response Levels 2 Number of Observations 12 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value y Frequency 1 1 6 2 0 6 Model Convergence Status Complete separation of data points detected. WARNING: The maximum likelihood estimate does not exist. WARNING: The LOGISTIC procedure continues in spite of the above warning. Results shown are based on the last maximum likelihood iteration. Validity of the model fit is questionable. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 18.636 4.091 SC 19.120 5.061 -2 Log L 16.636 0.091 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 16.5442 1 <.0001 Score 8.4392 1 0.0037 Wald 0.6267 1 0.4286 The LOGISTIC Procedure WARNING: The validity of the model fit is questionable. Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -86.6641 109.4 0.6276 0.4282 x 1 15.0812 19.0498 0.6267 0.4286 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits x >999.999 <0.001 >999.999 Association of Predicted Probabilities and Observed Responses Percent Concordant 100.0 Somers' D 1.000 Percent Discordant 0.0 Gamma 1.000 Percent Tied 0.0 Tau-a 0.545 Pairs 36 c 1.000NOTE: Be sure the check the log for warnings such as
these:
WARNING: There is a complete separation of data points. The maximum likelihood estimate does not exist.
WARNING: The LOGISTIC procedure continues in spite of the above warning. Results shown are based on the last maximum likelihood iteration. Validity of the model fit is
questionable.
proc logistic data=hypothet43 desc; model y = x1; run; The LOGISTIC Procedure Model Information Data Set WORK.HYPOTHET43 Response Variable y Number of Response Levels 2 Number of Observations 12 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value y Frequency 1 1 6 2 0 6 Model Convergence Status Quasicomplete separation of data points detected. WARNING: The maximum likelihood estimate may not exist. WARNING: The LOGISTIC procedure continues in spite of the above warning. Results shown are based on the last maximum likelihood iteration. Validity of the model fit is questionable. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 18.636 6.774 SC 19.120 7.744 -2 Log L 16.636 2.774 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 13.8613 1 0.0002 Score 8.1818 1 0.0042 Wald 0.0489 1 0.8249 The LOGISTIC Procedure WARNING: The validity of the model fit is questionable. Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -46.9574 212.3 0.0489 0.8249 x1 1 7.8262 35.3798 0.0489 0.8249 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits x1 >999.999 <0.001 >999.999 Association of Predicted Probabilities and Observed Responses Percent Concordant 97.2 Somers' D 0.972 Percent Discordant 0.0 Gamma 1.000 Percent Tied 2.8 Tau-a 0.530 Pairs 36 c 0.986NOTE: Be sure the check the log for warnings such as these:
WARNING: There is a complete separation of data points. The maximum likelihood estimate does not exist.
WARNING: The LOGISTIC procedure continues in spite of the above warning. Results shown are based on the last maximum likelihood iteration. Validity of the model fit is questionable.
proc logistic data=hypothet43 desc; model y = x2; run; The LOGISTIC Procedure Model Information Data Set WORK.HYPOTHET43 Response Variable y Number of Response Levels 2 Number of Observations 12 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value y Frequency 1 1 6 2 0 6 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 18.636 7.048 SC 19.120 8.018 -2 Log L 16.636 3.048 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 13.5873 1 0.0002 Score 8.1544 1 0.0043 Wald 0.5096 1 0.4753 Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -26.1725 36.7202 0.5080 0.4760 x2 1 4.3449 6.0865 0.5096 0.4753 The LOGISTIC Procedure Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits x2 77.082 <0.001 >999.999 Association of Predicted Probabilities and Observed Responses Percent Concordant 97.2 Somers' D 0.944 Percent Discordant 2.8 Gamma 0.944 Percent Tied 0.0 Tau-a 0.515 Pairs 36 c 0.972proc logistic data=hypothet43 desc; model y = x3; run; The LOGISTIC Procedure Model Information Data Set WORK.HYPOTHET43 Response Variable y Number of Response Levels 2 Number of Observations 12 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value y Frequency 1 1 6 2 0 6 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 18.636 7.261 SC 19.120 8.231 -2 Log L 16.636 3.261 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 13.3744 1 0.0003 Score 8.1267 1 0.0044 Wald 0.7547 1 0.3850 Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -21.9783 25.3985 0.7488 0.3869 x3 1 3.6356 4.1850 0.7547 0.3850 The LOGISTIC Procedure Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits x3 37.925 0.010 >999.999 Association of Predicted Probabilities and Observed Responses Percent Concordant 97.2 Somers' D 0.944 Percent Discordant 2.8 Gamma 0.944 Percent Tied 0.0 Tau-a 0.515 Pairs 36 c 0.972proc logistic data=hypothet43 desc; model y = x4; run; The LOGISTIC Procedure Model Information Data Set WORK.HYPOTHET43 Response Variable y Number of Response Levels 2 Number of Observations 12 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value y Frequency 1 1 6 2 0 6 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 18.636 7.452 SC 19.120 8.422 -2 Log L 16.636 3.452 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 13.1836 1 0.0003 Score 8.0987 1 0.0044 Wald 0.9341 1 0.3338 Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -19.5296 20.3399 0.9219 0.3370 x4 1 3.2202 3.3318 0.9341 0.3338 The LOGISTIC Procedure Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits x4 25.032 0.037 >999.999 Association of Predicted Probabilities and Observed Responses Percent Concordant 97.2 Somers' D 0.944 Percent Discordant 2.8 Gamma 0.944 Percent Tied 0.0 Tau-a 0.515 Pairs 36 c 0.972proc logistic data=hypothet43 desc; model y = x5; run; The LOGISTIC Procedure Model Information Data Set WORK.HYPOTHET43 Response Variable y Number of Response Levels 2 Number of Observations 12 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value y Frequency 1 1 6 2 0 6 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 18.636 7.629 SC 19.120 8.599 -2 Log L 16.636 3.629 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 13.0068 1 0.0003 Score 8.0704 1 0.0045 Wald 1.0791 1 0.2989 Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -17.8028 17.2983 1.0592 0.3034 x5 1 2.9269 2.8175 1.0791 0.2989 The LOGISTIC Procedure Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits x5 18.669 0.075 >999.999 Association of Predicted Probabilities and Observed Responses Percent Concordant 97.2 Somers' D 0.944 Percent Discordant 2.8 Gamma 0.944 Percent Tied 0.0 Tau-a 0.515 Pairs 36 c 0.972proc logistic data=hypothet43 desc; model y = x6; run; The LOGISTIC Procedure Model Information Data Set WORK.HYPOTHET43 Response Variable y Number of Response Levels 2 Number of Observations 12 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value y Frequency 1 1 6 2 0 6 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 18.636 11.560 SC 19.120 12.530 -2 Log L 16.636 7.560 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 9.0757 1 0.0026 Score 6.8974 1 0.0086 Wald 3.3103 1 0.0688 Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -6.1239 3.5853 2.9175 0.0876 x6 1 0.9665 0.5312 3.3103 0.0688 The LOGISTIC Procedure Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits x6 2.629 0.928 7.445 Association of Predicted Probabilities and Observed Responses Percent Concordant 91.7 Somers' D 0.861 Percent Discordant 5.6 Gamma 0.886 Percent Tied 2.8 Tau-a 0.470 Pairs 36 c 0.931
page 140 Table 4.20 Data displaying near collinearity among the independent variables and constant.
data hypothet42; input subj x1 x2 x3 y; cards; 1 .225 .231 1.026 0 2 .487 .489 1.022 1 3 -1.080 -1.070 1.074 0 4 -.87 -.87 1.091 0 5 -.58 -.57 1.095 0 6 -.64 -.64 1.01 0 7 1.614 1.619 1.087 0 8 .352 .355 1.095 1 9 -1.025 -1.018 1.008 0 10 .929 .937 1.057 1 ; run; proc print data=hypothet42 noobs; var subj x1 x2 x3 y; run; subj x1 x2 x3 y 1 0.225 0.231 1.026 0 2 0.487 0.489 1.022 1 3 -1.080 -1.070 1.074 0 4 -0.870 -0.870 1.091 0 5 -0.580 -0.570 1.095 0 6 -0.640 -0.640 1.010 0 7 1.614 1.619 1.087 0 8 0.352 0.355 1.095 1 9 -1.025 -1.018 1.008 0 10 0.929 0.937 1.057 1page 141 Table 4.21 Estimated coefficients and standard errors from fitting logistic regression models to the data in Table 4.20.
column 2
proc logistic data=hypothet42 desc; model y = x1; run; The LOGISTIC Procedure Model Information Data Set WORK.HYPOTHET42 Response Variable y Number of Response Levels 2 Number of Observations 10 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value y Frequency 1 1 3 2 0 7 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 14.217 13.743 SC 14.520 14.348 -2 Log L 12.217 9.743 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 2.4746 1 0.1157 Score 2.3798 1 0.1229 Wald 1.8850 1 0.1698 Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -1.0017 0.8294 1.4586 0.2272 x1 1 1.3803 1.0054 1.8850 0.1698 The LOGISTIC Procedure Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits x1 3.976 0.554 28.525 Association of Predicted Probabilities and Observed Responses Percent Concordant 85.7 Somers' D 0.714 Percent Discordant 14.3 Gamma 0.714 Percent Tied 0.0 Tau-a 0.333 Pairs 21 c 0.857column 3 Note that there is likely a typo in this column.
proc logistic data=hypothet42 desc; model y = x1 x2; run; The LOGISTIC Procedure Model Information Data Set WORK.HYPOTHET42 Response Variable y Number of Response Levels 2 Number of Observations 10 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value y Frequency 1 1 3 2 0 7 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 14.217 15.443 SC 14.520 16.350 -2 Log L 12.217 9.443 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 2.7748 2 0.2497 Score 2.5036 2 0.2860 Wald 1.8145 2 0.4036 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -0.3703 1.3625 0.0739 0.7858 x1 1 146.4 277.0 0.2793 0.5972 x2 1 -144.9 276.6 0.2744 0.6004 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits x1 >999.999 <0.001 >999.999 x2 <0.001 <0.001 >999.999 Association of Predicted Probabilities and Observed Responses Percent Concordant 85.7 Somers' D 0.714 Percent Discordant 14.3 Gamma 0.714 Percent Tied 0.0 Tau-a 0.333 Pairs 21 c 0.857column 4 Note that there is likely a typo in this column.
proc logistic data=hypothet42 desc; model y = x3; run; The LOGISTIC Procedure Model Information Data Set WORK.HYPOTHET42 Response Variable y Number of Response Levels 2 Number of Observations 10 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value y Frequency 1 1 3 2 0 7 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 14.217 16.209 SC 14.520 16.814 -2 Log L 12.217 12.209 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 0.0080 1 0.9286 Score 0.0080 1 0.9287 Wald 0.0080 1 0.9287 Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -2.7369 21.1278 0.0168 0.8969 x3 1 1.7878 19.9709 0.0080 0.9287 The LOGISTIC Procedure Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits x3 5.976 <0.001 >999.999 Association of Predicted Probabilities and Observed Responses Percent Concordant 52.4 Somers' D 0.095 Percent Discordant 42.9 Gamma 0.100 Percent Tied 4.8 Tau-a 0.044 Pairs 21 c 0.548column 5
proc logistic data=hypothet42 desc; model y = x1 x2 x3; run; The LOGISTIC Procedure Model Information Data Set WORK.HYPOTHET42 Response Variable y Number of Response Levels 2 Number of Observations 10 Link Function Logit Optimization Technique Fisher's scoring Response Profile Ordered Total Value y Frequency 1 1 3 2 0 7 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterion Only Covariates AIC 14.217 17.421 SC 14.520 18.632 -2 Log L 12.217 9.421 Testing Global Null Hypothesis: BETA=0 Test Chi-Square DF Pr > ChiSq Likelihood Ratio 2.7960 3 0.4242 Score 2.5110 3 0.4733 Wald 1.8145 3 0.6118 The LOGISTIC Procedure Analysis of Maximum Likelihood Estimates Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 3.4228 26.1558 0.0171 0.8959 x1 1 143.0 282.2 0.2567 0.6124 x2 1 -141.4 281.8 0.2519 0.6157 x3 1 -3.6208 24.9538 0.0211 0.8846 Odds Ratio Estimates Point 95% Wald Effect Estimate Confidence Limits x1 >999.999 <0.001 >999.999 x2 <0.001 <0.001 >999.999 x3 0.027 <0.001 >999.999 Association of Predicted Probabilities and Observed Responses Percent Concordant 85.7 Somers' D 0.714 Percent Discordant 14.3 Gamma 0.714 Percent Tied 0.0 Tau-a 0.333 Pairs 21 c 0.857