This chapter uses two data files. They are
https://stats.idre.ucla.edu/wp-content/uploads/2016/02/lowbwt11.sas7bdat for the first example and
https://stats.idre.ucla.edu/wp-content/uploads/2016/02/bbdm13.sas7bdat for the second example. A new procedure proc mdc (multinomial discrete choice) in SAS 8.2 is the procedure that we will use mainly for parameter estimates. One feature that proc mdc lacks is the class statement. Therefore, we have to create dummy variables for a categorical variable through a data step. For example, in a data step in section 7.3, we created two dummy variables for variable race and this new data set will be used throughout the first two sections. The other issue is that the diagnostic graphs are not generated by the procedure. We will have to use proc logistic as mentioned in the book to carry out analyses in section 7.4 and 7.7.
7.3 An example of the use of the logistic regression model in a 1-1 matched study
Table 7.1 on page 232.
data lowbwt11a; set lowbwt11; race2 = (race=2); race3 = (race=3); lwt10 = lwt/10; run; ods listing close; /*first row on variable lwt*/ proc mdc data = lowbwt11a ; model low = lwt /type = clogit nchoice=2 ; id pair; ods output ParameterEstimates = parms1; run; /*obtain odds ratio for 10 pound increase in weight*/ proc mdc data = lowbwt11a ; model low = lwt10 /type = clogit nchoice=2; id pair; ods output ParameterEstimates = parms2; run; /*second row on variable smoke*/ proc mdc data = lowbwt11a ; model low = smoke /type = clogit nchoice=2; id pair; ods output ParameterEstimates = parms3; run; /*on variable race, overall*/ proc mdc data = lowbwt11a ; model low = race2 race3 /type = clogit nchoice=2; id pair; ods output ParameterEstimates = parms4; run; /*on variable ptd*/ proc mdc data = lowbwt11a ; model low = ptd /type = clogit nchoice=2; id pair; ods output ParameterEstimates = parms5; run; /*on variable ht*/ proc mdc data = lowbwt11a ; model low = ht /type = clogit nchoice=2; id pair; ods output ParameterEstimates = parms6; run; /*on variable ui*/ proc mdc data = lowbwt11a ; model low = ui /type = clogit nchoice=2; id pair; ods output ParameterEstimates = parms7; run; ods listing; /*putting all the estimates together*/ data table7_1; set parms1 parms2 parms3 parms4 parms5 parms6 parms7; or = exp(estimate); cilow = exp(estimate - 1.96*stderr); cihigh = exp(estimate + 1.96*stderr); run; proc print data = table7_1 noobs; var parameter estimate stderr or cilow cihigh; run;
Parameter Estimate StdErr or cilow cihigh lwt -0.009375 0.006165 0.99067 0.97877 1.0027 lwt10 -0.0937 0.0617 0.91051 0.80687 1.0275 smoke 1.0116 0.4129 2.75000 1.22433 6.1769 race2 0.0870 0.5233 1.09095 0.39116 3.0427 race3 -0.0290 0.3968 0.97142 0.44632 2.1143 ptd 1.3218 0.5627 3.75000 1.24458 11.2989 ht 0.8473 0.6901 2.33333 0.60337 9.0234 ui 1.0986 0.5774 3.00000 0.96754 9.3019
Last column of Table 7.1
proc sql; create table dispairs as select *, sum(smoke) as smoke_count, sum(ptd) as ptd_count, sum(ht) as ht_count, sum(ui) as ui_count from lowbwt11a group by pair; quit; proc freq data = dispairs; where smoke_count = 1; tables low*smoke /nopercent nocol norow ; run; proc freq data = dispairs; where ptd_count = 1; tables low*ptd /nopercent nocol norow ; run; proc freq data = dispairs; where ht_count = 1; tables low*ht /nopercent nocol norow ; run; proc freq data = dispairs; where ui_count = 1; tables low*ui /nopercent nocol norow ; run;
Table of low by smoke
low smoke
Frequency 0 1 Total
--------- -------- --------
0 22 8 30
--------- -------- --------
1 8 22 30
--------- -------- --------
Total 30 30 60
Table of low by ptd
low ptd
Frequency 0 1 Total
--------- -------- --------
0 15 4 19
--------- -------- --------
1 4 15 19
--------- -------- --------
Total 19 19 38
Table of low by ht
low ht
Frequency 0 1 Total
--------- -------- --------
0 7 3 10
--------- -------- --------
1 3 7 10
--------- -------- --------
Total 10 10 20
Table of low by ui
low ui
Frequency 0 1 Total
--------- -------- --------
0 12 4 16
--------- -------- --------
1 4 12 16
--------- -------- --------
Total 16 16 32
Table 7.2 on page 232.
proc mdc data = lowbwt11a ; model low = lwt smoke race2 race3 ptd ht ui /type = clogit nchoice=2; id pair; run;
The MDC Procedure
Conditional Logit Estimates
Model Fit Summary
Dependent Variable low
Number of Observations 56
Number of Cases 112
Log Likelihood -25.79427
Maximum Absolute Gradient 2.30684E-6
Number of Iterations 5
Optimization Method Newton-Raphson
AIC 65.58854
Schwarz Criterion 79.76600
Discrete Response Profile
Index CHOICE Frequency Percent
0 1 0 0.00
1 2 56 100.00
Goodness-of-Fit Measures for Discrete Choice Models
Measure Value Formula
Likelihood Ratio (R) 26.044 2 * (LogL - LogL0)
Upper Bound of R (U) 77.632 - 2 * LogL0
Aldrich-Nelson 0.3174 R / (R+N)
Cragg-Uhler 1 0.3719 1 - exp(-R/N)
Cragg-Uhler 2 0.4959 (1-exp(-R/N)) / (1-exp(-U/N))
Estrella 0.4325 1 - (1-R/U)^(U/N)
Adjusted Estrella 0.2084 1 - ((LogL-K)/LogL0)^(-2/N*LogL0)
McFadden's LRI 0.3355 R / U
Veall-Zimmermann 0.5464 (R * (U+N)) / (U * (R+N))
N = # of observations, K = # of regressors
Parameter Estimates
Standard Approx
Parameter DF Estimate Error t Value Pr > |t| Gradient
lwt 1 -0.0184 0.0101 -1.82 0.0683 -2.31E-6
smoke 1 1.4007 0.6278 2.23 0.0257 3.741E-8
race2 1 0.5714 0.6896 0.83 0.4074 8.89E-10
race3 1 -0.0253 0.6992 -0.04 0.9711 -2.35E-9
ptd 1 1.8080 0.7887 2.29 0.0219 4.792E-8
ht 1 2.3612 1.0861 2.17 0.0297 1.5E-8
ui 1 1.4019 0.6962 2.01 0.0440 1.25E-8
Table 7.3 on page 233.
proc mdc data = lowbwt11a ; model low = lwt smoke ptd ht ui /type = clogit nchoice=2; id pair; run;
The MDC Procedure
Conditional Logit Estimates
Model Fit Summary
Dependent Variable low
Number of Observations 56
Number of Cases 112
Log Likelihood -26.23687
Maximum Absolute Gradient 8.97556E-7
Number of Iterations 5
Optimization Method Newton-Raphson
AIC 62.47374
Schwarz Criterion 72.60050
Discrete Response Profile
Index CHOICE Frequency Percent
0 1 0 0.00
1 2 56 100.00
Goodness-of-Fit Measures for Discrete Choice Models
Measure Value Formula
Likelihood Ratio (R) 25.159 2 * (LogL - LogL0)
Upper Bound of R (U) 77.632 - 2 * LogL0
Aldrich-Nelson 0.3100 R / (R+N)
Cragg-Uhler 1 0.3619 1 - exp(-R/N)
Cragg-Uhler 2 0.4825 (1-exp(-R/N)) / (1-exp(-U/N))
Estrella 0.4190 1 - (1-R/U)^(U/N)
Adjusted Estrella 0.2600 1 - ((LogL-K)/LogL0)^(-2/N*LogL0)
McFadden's LRI 0.3241 R / U
Veall-Zimmermann 0.5336 (R * (U+N)) / (U * (R+N))
N = # of observations, K = # of regressors
Parameter Estimates
Standard Approx
Parameter DF Estimate Error t Value Pr > |t| Gradient
lwt 1 -0.0151 0.008147 -1.85 0.0641 -8.98E-7
smoke 1 1.4796 0.5620 2.63 0.0085 1.571E-8
ptd 1 1.6706 0.7468 2.24 0.0253 1.768E-8
ht 1 2.3294 1.0025 2.32 0.0202 4.155E-9
ui 1 1.3449 0.6938 1.94 0.0526 6.344E-9
Table 7.4 on page 233. SAS doesn’t have a procedure that handles fractional polynomial regressions. We can only verify the table here, instead of creating it. Notice the deviance is -2*(Log Likelihood). For example, in the first model below, we have -2*(-28.14929) = 56.29858.
data test7_4; set lowbwt11a; lwt3 = lwt**3; lwt31 = lwt3*log(lwt); run;proc mdc data = test7_4 ; model low = smoke ptd ht ui /type = clogit nchoice=2; id pair; run; Model Fit Summary Dependent Variable low Number of Observations 56 Number of Cases 112 Log Likelihood -28.14929 Maximum Absolute Gradient 2.7136E-11 Number of Iterations 5 Optimization Method Newton-Raphson AIC 64.29857 Schwarz Criterion 72.39998Model 1: without variable lwt.
Model 2: with variable lwt as a linear term.
proc mdc data = test7_4 ;
model low = smoke lwt ptd ht ui /type = clogit nchoice=2;
id pair;
run;
Model Fit Summary
Dependent Variable low
Number of Observations 56
Number of Cases 112
Log Likelihood -26.23687
Maximum Absolute Gradient 8.97556E-7
Number of Iterations 5
Optimization Method Newton-Raphson
AIC 62.47374
Schwarz Criterion 72.60050
The deviance is -2*(-26.23687) = 52.47374. The difference in deviance between the first model and the current one is 56.299-52.474 = 3.825. The p-value is computed based on chi-squared distribution with 1 degree of freedom. This gives p-value 0.050493.
Model 3: with variable lwt as a third polynomial term.
proc mdc data = test7_4 ;
model low = smoke lwt3 ptd ht ui /type = clogit nchoice=2;
id pair;
run;
Model Fit Summary
Dependent Variable low
Number of Observations 56
Number of Cases 112
Log Likelihood -25.77035
Maximum Absolute Gradient 0.05711
Number of Iterations 5
Optimization Method Newton-Raphson
AIC 61.54070
Schwarz Criterion 71.66746
The deviance is -2*(-25.77035) =51.5407. The difference in deviance between the second model and the current one is 52.474 – 51.5407 = .9333. The p-value is computed based on chi-squared distribution with 1 degree of freedom. This gives p-value 0.334.
Model 4: with variable lwt transformed as lwt^3*ln(lwt).
proc mdc data = test7_4 ;
model low = smoke lwt3 lwt31 ptd ht ui /type = clogit nchoice=2;
id pair;
run;
Model Fit Summary
Dependent Variable low
Number of Observations 56
Number of Cases 112
Log Likelihood -25.61927
Maximum Absolute Gradient 1.51806E-6
Number of Iterations 6
Optimization Method Newton-Raphson
AIC 63.23855
Schwarz Criterion 75.39066
The deviance is -2*(-25.61927) =51.23854. The difference in deviance between the third model and the current one is 51.5407 – 51.23854 = .3025 and the difference between the second model and the current one is 52.474 – 51.239 = 1.235. The p-value is computed based on chi-squared distribution with 2 degrees of freedom and the difference in deviance between the third model and the current one. This gives a p-value of 0.860.
Table 7.5 on page 234.
proc univariate data = lowbwt11a ; var lwt; run; (Some output omitted) Quantile Estimate 100% Max 241.0 99% 235.0 95% 190.0 90% 168.0 75% Q3 136.5 50% Median 120.0 25% Q1 106.5 10% 95.0 5% 91.0 1% 85.0 0% Min 80.0
data table7_5; set lowbwt11a; lwt1 = (lwt <= 106.5); lwt2 = (lwt >106.5 & lwt <=120); lwt3 = (lwt >120 & lwt <=136.5); lwt4 = (lwt >136.5 ); run; proc mdc data = table7_5; model low = lwt2-lwt4 smoke ptd ht ui /type = clogit nchoice=2; id pair; run;
Conditional Logit Estimates
Goodness-of-Fit Measures for Discrete Choice Models
Measure Value Formula
Veall-Zimmermann 0.5096 (R * (U+N)) / (U * (R+N))
N = # of observations, K = # of regressors
Parameter Estimates
Standard Approx
Parameter DF Estimate Error t Value Pr > |t| Gradient
lwt2 1 -0.3991 0.6635 -0.60 0.5475 -2.16E-9
lwt3 1 -0.4430 0.6718 -0.66 0.5096 1.085E-9
lwt4 1 -0.8887 0.6255 -1.42 0.1553 -2.14E-9
smoke 1 1.3527 0.5568 2.43 0.0151 3.108E-9
ptd 1 1.7398 0.7462 2.33 0.0197 4.2E-9
ht 1 1.8926 0.9647 1.96 0.0498 1.351E-9
ui 1 1.3162 0.6886 1.91 0.0559 1.549E-9
Figure 7.1 on page 234.
data fig7_1; input coef2go lwt2go; datalines; 0 93.25 -.399 113.25 -.433 128.25 -.889 188.75 ; run; symbol i = join c = black; axis1 label = (a = 90) minor = none; proc gplot data = fig7_1; plot coef2go*lwt2go /vaxis=axis1; label coef2go = "Estimated Coefficient"; label lwt2go = "Weight at the Last Menstrual Period"; run; quit;
Table 7.6 on page 235. This is fairly long table comparing a lot of possible interaction terms with model presented in Table 7.3. We only present code for the first row of the table testing interaction term on age and lwt. The other rows of the table can be generated exactly the same way and we omit them here.
data table7_6; set lowbwt11a; agelwt = age*lwt; run; ods listing close; proc mdc data = table7_6; model low = lwt smoke ptd ht ui /type = clogit nchoice=2; id pair; ods output FitSummary = w_o_interacton; run; proc mdc data = table7_6; model low = lwt smoke ptd ht ui agelwt/type = clogit nchoice=2; id pair; ods output FitSummary = w_interaction; run; ods listing; proc sql; create table row1 as select w1.cvalue1 as w_o_ll, w2.cvalue1 as w_ll from w_o_interacton as w1, w_interaction as w2 where w1.label1="Log Likelihood" & w2.label1="Log Likelihood"; quit; data row1; set row1; g = 2*(w_ll - w_o_ll); p = 1- PROBCHI(g, 1); output; run; proc print data = row1; run; Obs w_o_ll w_ll t p 1 -26.23687 -25.98409 0.50556 0.47707
7.4 Assessment of fit in a matched study
As we have mentioned at the beginning of this chapter, SAS proc mdc does not offer diagnostic statistics. We follow the method discussed in the book using the difference variables.
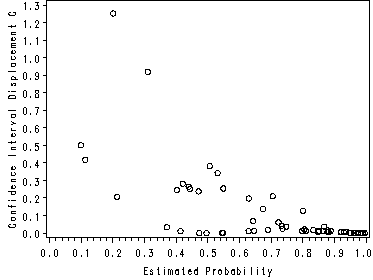
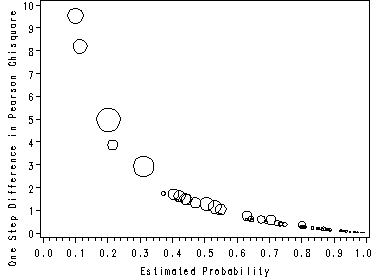
Figure 7.2, Figure 7.3 and Figure 7.4.
data assess; set lowbwt11a; retain lwt1 smoke1 ptd1 ht1 ui1; by pair; if first.pair then do; lwt1 = lwt; smoke1 = smoke; ptd1 = ptd; ht1 = ht; ui1 = ui; end; else do; lwt1 = lwt - lwt1; smoke1 = smoke - smoke1; ptd1 = ptd - ptd1; ht1 = ht - ht1; ui1 = ui - ui1; output; end; keep low lwt1 smoke1 ptd1 ht1 ui1 ; run; proc logistic data = assess; model low = lwt1 smoke1 ptd1 ht1 ui1 /noint; output out = test difchisq = _dx2 c = dbeta p = p ; run; goptions reset = all; symbol v = circle c = black; axis1 label = (a=90) minor = none; proc gplot data = test; plot _dx2*p /vaxis = axis1; plot dbeta*p /vaxis=axis1; bubble _dx2*p = dbeta / bsize = 10 vaxis=axis1; run; quit;
Table 7.7 on page 240.
proc logistic data = assess; model low = lwt1 smoke1 ptd1 ht1 ui1 /noint; output out = test difchisq = _dx2 c = dbeta p = p h = h ; run; proc print data = test (drop=_level_); where dbeta >.4; format lwt1 smoke1 ptd1 ht1 ui1 4.0 p dbeta difchisq _dx2 h 4.2; run;
Obs low lwt1 smoke1 ptd1 ht1 ui1 p h dbeta _dx2 9 1 48 -1 0 0 0 0.10 0.05 0.50 9.53 16 1 -49 1 -1 0 -1 0.31 0.24 0.92 2.92 27 1 35 1 0 -1 0 0.20 0.20 1.25 4.97 34 1 38 -1 0 0 0 0.11 0.05 0.42 8.19
Table 7.8 on page 241 .
proc logistic data = assess; model low = lwt1 smoke1 ptd1 ht1 ui1 /noint AGGREGATE scale=none; run;
Deviance and Pearson Goodness-of-Fit Statistics
Criterion DF Value Value/DF Pr > ChiSq
Deviance 51 52.4737 1.0289 0.4167
Pearson 51 50.7566 0.9952 0.4833
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
lwt1 1 -0.0151 0.00815 3.4281 0.0641
smoke1 1 1.4796 0.5620 6.9305 0.0085
ptd1 1 1.6706 0.7468 5.0041 0.0253
ht1 1 2.3294 1.0025 5.3984 0.0202
ui1 1 1.3449 0.6938 3.7571 0.0526
data table7_8; set assess; id = _n_; run; proc logistic data = table7_8; model low = lwt1 smoke1 ptd1 ht1 ui1 /noint AGGREGATE scale=none; where id ~=9; run;
Deviance and Pearson Goodness-of-Fit Statistics
Criterion DF Value Value/DF Pr > ChiSq
Deviance 50 47.3316 0.9466 0.5811
Pearson 50 48.5205 0.9704 0.5329
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
lwt1 1 -0.0196 0.00910 4.6473 0.0311
smoke1 1 1.8781 0.6545 8.2334 0.0041
ptd1 1 1.8831 0.8279 5.1732 0.0229
ht1 1 2.7193 1.1184 5.9123 0.0150
ui1 1 1.4979 0.7317 4.1904 0.0407
proc logistic data = table7_8;
model low = lwt1 smoke1 ptd1 ht1 ui1 /noint AGGREGATE scale=none;
where id ~=16;
run;
Deviance and Pearson Goodness-of-Fit Statistics
Criterion DF Value Value/DF Pr > ChiSq
Deviance 50 49.4140 0.9883 0.4968
Pearson 50 46.3723 0.9274 0.6197
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
lwt1 1 -0.0126 0.00836 2.2653 0.1323
smoke1 1 1.3907 0.5681 5.9933 0.0144
ptd1 1 2.1109 0.8577 6.0563 0.0139
ht1 1 2.4069 1.0304 5.4564 0.0195
ui1 1 1.7624 0.7886 4.9950 0.0254
proc logistic data = table7_8;
model low = lwt1 smoke1 ptd1 ht1 ui1 /noint AGGREGATE scale=none;
where id ~=27;
run;
Deviance and Pearson Goodness-of-Fit Statistics
Criterion DF Value Value/DF Pr > ChiSq
Deviance 50 48.1354 0.9627 0.5485
Pearson 50 49.0020 0.9800 0.5134
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
lwt1 1 -0.0211 0.00917 5.2675 0.0217
smoke1 1 1.3894 0.5888 5.5673 0.0183
ptd1 1 1.8071 0.7963 5.1497 0.0233
ht1 1 3.5595 1.4073 6.3977 0.0114
ui1 1 1.5107 0.7336 4.2412 0.0395
proc logistic data = table7_8;
model low = lwt1 smoke1 ptd1 ht1 ui1 /noint AGGREGATE scale=none;
where id ~=34;
run;
Deviance and Pearson Goodness-of-Fit Statistics
Criterion DF Value Value/DF Pr > ChiSq
Deviance 50 47.6911 0.9538 0.5665
Pearson 50 50.3025 1.0060 0.4614
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
lwt1 1 -0.0188 0.00896 4.3979 0.0360
smoke1 1 1.8548 0.6487 8.1742 0.0042
ptd1 1 1.8630 0.8191 5.1736 0.0229
ht1 1 2.6686 1.1029 5.8548 0.0155
ui1 1 1.4866 0.7284 4.1654 0.0413
Table 7.9 on page 242.
proc logistic data = table7_8;
model low = lwt1 smoke1 ptd1 ht1 ui1 /noint clodds = wald;
units lwt1 = 10;
run;
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
lwt1 1 -0.0151 0.00815 3.4281 0.0641
smoke1 1 1.4796 0.5620 6.9305 0.0085
ptd1 1 1.6706 0.7468 5.0041 0.0253
ht1 1 2.3294 1.0025 5.3984 0.0202
ui1 1 1.3449 0.6938 3.7571 0.0526
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
lwt1 0.985 0.969 1.001
smoke1 4.391 1.459 13.212
ptd1 5.315 1.230 22.973
ht1 10.271 1.440 73.283
ui1 3.838 0.985 14.951
Wald Confidence Interval for Adjusted Odds Ratios Effect Unit Estimate 95% Confidence Limits lwt1 10.0000 0.860 0.733 1.009
7.5 An example of the use of the logistic regression model in a 1-M matched study 
For this section, we omit the calculation of odds ratio after proc mdc. The calculation is shown in the first section of this chapter and is the same calculation here.
Table 7.11 on page 246.
proc mdc data = bbdm13;
model fndx = chk /type = clogit nchoice=4;
id str;
run;
Conditional Logit Estimates
Model Fit Summary
Dependent Variable fndx
Number of Observations 50
Number of Cases 200
Log Likelihood -62.81737
Maximum Absolute Gradient 2.03546E-9
Number of Iterations 4
Optimization Method Newton-Raphson
AIC 127.63473
Schwarz Criterion 129.54676
Goodness-of-Fit Measures for Discrete Choice Models
Measure Value Formula
Likelihood Ratio (R) 12.995 2 * (LogL - LogL0)
Upper Bound of R (U) 138.63 - 2 * LogL0
Aldrich-Nelson 0.2063 R / (R+N)
Cragg-Uhler 1 0.2289 1 - exp(-R/N)
Cragg-Uhler 2 0.2441 (1-exp(-R/N)) / (1-exp(-U/N))
Estrella 0.2388 1 - (1-R/U)^(U/N)
Adjusted Estrella 0.2048 1 - ((LogL-K)/LogL0)^(-2/N*LogL0)
McFadden's LRI 0.0937 R / U
Veall-Zimmermann 0.2807 (R * (U+N)) / (U * (R+N))
N = # of observations, K = # of regressors
Parameter Estimates
Standard Approx
Parameter DF Estimate Error t Value Pr > |t| Gradient
chk 1 -1.2454 0.3815 -3.26 0.0011 -2.04E-9
proc mdc data = bbdm13; model fndx = agmn /type = clogit nchoice=4; id str; run;
Parameter Estimates
Standard Approx
Parameter DF Estimate Error t Value Pr > |t| Gradient
agmn 1 0.4718 0.1110 4.25 <.0001 1.21E-11
proc mdc data = bbdm13; model fndx = wt /type = clogit nchoice=4; id str; run;
Parameter Estimates
Standard Approx
Parameter DF Estimate Error t Value Pr > |t| Gradient
wt 1 -0.0352 0.008599 -4.09 <.0001 -5.76E-9
data bbdm13a; bbdm13; mst2 = ( mst = 2 | mst = 3); mst4 = ( mst = 4); mst5 = ( mst = 5); run; proc mdc data = bbdm13a; model fndx = mst2 mst4 mst5 /type = clogit nchoice=4; id str; run;
Parameter Estimates
Standard Approx
Parameter DF Estimate Error t Value Pr > |t| Gradient
mst2 1 -0.3584 0.5605 -0.64 0.5225 5.47E-11
mst4 1 -0.7510 0.7904 -0.95 0.3420 -364E-12
mst5 1 1.2484 0.6059 2.06 0.0393 9.22E-11
Table 7.12 on page 247.
proc mdc data = bbdm13; model fndx = chk agmn wt mst2 mst4 mst5 /type = clogit nchoice=4; id str; run;
The MDC Procedure
Conditional Logit Estimates
Model Fit Summary
Dependent Variable fndx
Number of Observations 50
Number of Cases 200
Log Likelihood -45.21482
Maximum Absolute Gradient 2.37731E-6
Number of Iterations 5
Optimization Method Newton-Raphson
AIC 102.42965
Schwarz Criterion 113.90179
Parameter Estimates
Standard Approx
Parameter DF Estimate Error t Value Pr > |t| Gradient
chk 1 -1.1218 0.4474 -2.51 0.0122 -2.21E-8
agmn 1 0.3561 0.1292 2.76 0.0058 8.038E-8
wt 1 -0.0284 0.009978 -2.84 0.0045 -2.38E-6
mst2 1 -0.2030 0.6473 -0.31 0.7538 -3.36E-9
mst4 1 -0.4916 0.8173 -0.60 0.5475 -1.21E-9
mst5 1 1.4722 0.7582 1.94 0.0522 7.341E-9
Table 7.13 on page 247.
proc mdc data = bbdm13; model fndx = chk agmn wt mst5 /type = clogit nchoice=4; id str; run;
The MDC Procedure
Conditional Logit Estimates
Model Fit Summary
Dependent Variable fndx
Number of Observations 50
Number of Cases 200
Log Likelihood -45.43901
Maximum Absolute Gradient 2.22381E-6
Number of Iterations 5
Optimization Method Newton-Raphson
AIC 98.87802
Schwarz Criterion 106.52611
Parameter Estimates
Standard Approx
Parameter DF Estimate Error t Value Pr > |t| Gradient
chk 1 -1.1613 0.4470 -2.60 0.0094 -2E-8
agmn 1 0.3592 0.1279 2.81 0.0050 7.529E-8
wt 1 -0.0282 0.009978 -2.83 0.0047 -2.22E-6
mst5 1 1.5934 0.7360 2.16 0.0304 6.713E-9
7.7 An example of assessment of fit in a 1-M matched study
Currently, SAS does not offer the diagnostics discussed in this section. Stata has an add-on program called clfit that will generate these diagnostic variables after clogit. Please see Chapter 7 in Stata for more detail.