3.2 Dichotomous independent variable
page 51 Table 3.2 Cross-classification of AGE dichotomized at 55 years and CHD for 100 subjects.
data chdage31;
set 'd:hosmerdatachdage';
aged=0;
if age ge 55 then aged=1;
run;
proc sort data=chdage31 out=chdage32;
by aged;
run;
proc freq data=chdage32;
tables chd*aged;
run;
The FREQ Procedure
Table of CHD by aged
CHD aged
Frequency|
Percent |
Row Pct |
Col Pct | 0| 1| Total
---------+--------+--------+
0 | 51 | 6 | 57
| 51.00 | 6.00 | 57.00
| 89.47 | 10.53 |
| 69.86 | 22.22 |
---------+--------+--------+
1 | 22 | 21 | 43
| 22.00 | 21.00 | 43.00
| 51.16 | 48.84 |
| 30.14 | 77.78 |
---------+--------+--------+
Total 73 27 100
73.00 27.00 100.00
page 52 Table 3.3 Results of fitting the logistic regression model to the data in Table 3.2.
NOTE: To get the Wald tests shown in the text, take the square root of the chi-squares given in the SAS output.
NOTE: We have bolded the relevant output.
proc logistic data=chdage32 desc;
model chd = aged;
run;
quit;
The LOGISTIC Procedure
Model Information
Data Set WORK.CHDAGE32
Response Variable CHD
Number of Response Levels 2
Number of Observations 100
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value CHD Frequency
1 1 43
2 0 57
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 138.663 121.959
SC 141.268 127.169
-2 Log L 136.663 117.959
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 18.7039 1 <.0001
Score 18.2516 1 <.0001
Wald 15.6898 1 <.0001
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -0.8408 0.2551 10.8652 0.0010
aged 1 2.0935 0.5285 15.6898 <.0001
The LOGISTIC Procedure
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
aged 8.114 2.880 22.861
Association of Predicted Probabilities and Observed Responses
Percent Concordant 43.7 Somers' D 0.383
Percent Discordant 5.4 Gamma 0.781
Percent Tied 50.9 Tau-a 0.190
Pairs 2451 c 0.692
3.3 Polychotomous Independent Variable
page 56 Table 3.5 Cross-classification of hypothetical data on RACE and CHD status for 100 subjects.
data hypothet1;
input race chd cnt;
cards;
1 1 5
2 1 20
3 1 15
4 1 10
1 0 20
2 0 10
3 0 10
4 0 10
;
run;
proc freq data=hypothet1;
tables chd*race;
weight cnt;
run;
The FREQ Procedure
Table of chd by race
chd race
Frequency|
Percent |
Row Pct |
Col Pct | 1| 2| 3| 4| Total
---------+--------+--------+--------+--------+
0 | 20 | 10 | 10 | 10 | 50
| 20.00 | 10.00 | 10.00 | 10.00 | 50.00
| 40.00 | 20.00 | 20.00 | 20.00 |
| 80.00 | 33.33 | 40.00 | 50.00 |
---------+--------+--------+--------+--------+
1 | 5 | 20 | 15 | 10 | 50
| 5.00 | 20.00 | 15.00 | 10.00 | 50.00
| 10.00 | 40.00 | 30.00 | 20.00 |
| 20.00 | 66.67 | 60.00 | 50.00 |
---------+--------+--------+--------+--------+
Total 25 30 25 20 100
25.00 30.00 25.00 20.00 100.00
data hypothet2;
set hypothet1;
if race = 1 then do; race2 = 0; race3 = 0; race4 = 0; end;
if race = 2 then do; race2 = 1; race3 = 0; race4 = 0; end;
if race = 3 then do; race2 = 0; race3 = 1; race4 = 0; end;
if race = 4 then do; race2 = 0; race3 = 0; race4 = 1; end;
run;
proc logistic data=hypothet2 desc;
model chd = race2 race3 race4;
weight cnt;
run;
quit;
The LOGISTIC Procedure
Model Information
Data Set WORK.HYPOTHET2
Response Variable chd
Number of Response Levels 2
Number of Observations 8
Weight Variable cnt
Sum of Weights 100
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total Total
Value chd Frequency Weight
1 1 4 50.000000
2 0 4 50.000000
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 140.629 132.587
SC 140.709 132.905
-2 Log L 138.629 124.587
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 14.0420 3 0.0028
Score 13.3333 3 0.0040
Wald 11.7715 3 0.0082
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.3863 0.5000 7.6871 0.0056
race2 1 2.0794 0.6325 10.8100 0.0010
race3 1 1.7917 0.6455 7.7048 0.0055
race4 1 1.3863 0.6708 4.2706 0.0388
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
race2 8.000 2.316 27.633
race3 6.000 1.693 21.261
race4 4.000 1.074 14.895
Association of Predicted Probabilities and Observed Responses
Percent Concordant 37.5 Somers' D 0.000
Percent Discordant 37.5 Gamma 0.000
Percent Tied 25.0 Tau-a 0.000
Pairs 16 c 0.500
page 57 Table 3.6 Specification of the design variables for RACE using reference cell coding with white as the reference group.
proc print data=hypothet2 (obs=4); var race race2 race3 race4; run; Obs race race2 race3 race4 1 1 0 0 0 2 2 1 0 0 3 3 0 1 0 4 4 0 0 1
page 58 Table 3.7 Results of fitting the logistic regression model to the data in Table 3.5 using the design variables in Table 3.6.
proc logistic data=hypothet2 desc;
model chd = race2 race3 race4;
weight cnt;
run;
quit;
The LOGISTIC Procedure
Model Information
Data Set WORK.HYPOTHET2
Response Variable chd
Number of Response Levels 2
Number of Observations 8
Weight Variable cnt
Sum of Weights 100
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total Total
Value chd Frequency Weight
1 1 4 50.000000
2 0 4 50.000000
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 140.629 132.587
SC 140.709 132.905
-2 Log L 138.629 124.587
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 14.0420 3 0.0028
Score 13.3333 3 0.0040
Wald 11.7715 3 0.0082
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.3863 0.5000 7.6871 0.0056
race2 1 2.0794 0.6325 10.8100 0.0010
race3 1 1.7917 0.6455 7.7048 0.0055
race4 1 1.3863 0.6708 4.2706 0.0388
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
race2 8.000 2.316 27.633
race3 6.000 1.693 21.261
race4 4.000 1.074 14.895
Association of Predicted Probabilities and Observed Responses
Percent Concordant 37.5 Somers' D 0.000
Percent Discordant 37.5 Gamma 0.000
Percent Tied 25.0 Tau-a 0.000
Pairs 16 c 0.500
page 59 Table 3.8 Specification of the design variables for RACE using deviation from means coding.
data hypothet2; set hypothet1; if race = 1 then do; race2 = -1; race3 = -1; race4 = -1; end; if race = 2 then do; race2 = 1; race3 = 0; race4 = 0; end; if race = 3 then do; race2 = 0; race3 = 1; race4 = 0; end; if race = 4 then do; race2 = 0; race3 = 0; race4 = 1; end; run; proc print data=hypothet2 (obs=4); var race race2 race3 race4; run; Obs race race2 race3 race4 1 1 -1 -1 -1 2 2 1 0 0 3 3 0 1 0 4 4 0 0 1
page 60 Table 3.9 Results of fitting the logistic regression model to the data in Table 3.5 using the design variables in Table 3.8.
NOTE: To get the Wald tests shown in the text, take the square root of the chi-squares given in the SAS output. If the coefficient is negative, then you need to put the negative sign in front of the result of the square root.
proc logistic data=hypothet2 desc;
model chd = race2 race3 race4;
weight cnt;
run;
quit;
The LOGISTIC Procedure
Model Information
Data Set WORK.HYPOTHET2
Response Variable chd
Number of Response Levels 2
Number of Observations 8
Weight Variable cnt
Sum of Weights 100
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total Total
Value chd Frequency Weight
1 1 4 50.000000
2 0 4 50.000000
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 140.629 132.587
SC 140.709 132.905
-2 Log L 138.629 124.587
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 14.0420 3 0.0028
Score 13.3333 3 0.0040
Wald 11.7715 3 0.0082
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -0.0719 0.2189 0.1079 0.7425
race2 1 0.7651 0.3506 4.7619 0.0291
race3 1 0.4774 0.3623 1.7363 0.1876
race4 1 0.0719 0.3846 0.0350 0.8517
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
race2 2.149 1.081 4.273
race3 1.612 0.792 3.279
race4 1.075 0.506 2.284
Association of Predicted Probabilities and Observed Responses
Percent Concordant 37.5 Somers' D 0.000
Percent Discordant 37.5 Gamma 0.000
Percent Tied 25.0 Tau-a 0.000
Pairs 16 c 0.500
3.5 The multivariable model
page 67 Table 3.10 Descriptive statistics for two groups of 50 men on AGE and whether they had seen a physician (PHY) (1 = yes, 0 = no) within the last six months.
NOTE: These data are hypothetical and are not available.
page 69 Table 3.11 Results of fitting the logistic regression model to the data summarized in Table 3.10.
NOTE: These data are hypothetical and are not available.
3.6 Interaction and confounding
page 72 Table 3.12 Estimated logistic regression coefficients, deviance, and the likelihood ratio test statistic (G) for an example showing evidence of confounding but no interaction (n = 400).
NOTE: These data are hypothetical and are not available.
page 73 Table 3.13 Estimated logistic regression coefficients, deviance, and the likelihood ratio test statistic (G) for an example showing evidence of confounding and interaction (n = 400).
NOTE: These data are hypothetical and are not available.
3.7 Estimation of odds ratios in the presence of interaction
page 77 Table 3.14 Estimated logistic regression coefficients, deviance, and the likelihood ratio test statistic (G), and the p-value for the change for models containing lwd and age from the low birthweight data (n = 189).
NOTE: You need to calculate G by hand by subtracting the -2 log likelihood for the reduced model from the full model.
data lowbwt31;
set 'd:hosmerdatalowbwt';
if race = 1 then do; race2 = 0; race3 = 0; end;
if race = 2 then do; race2 = 1; race3 = 0; end;
if race = 3 then do; race2 = 0; race3 = 1; end;
lwd=(lwt<110);
run;
proc logistic data=lowbwt31 descending;
model low = lwd age lwd*age;
output out=lowbwt32 predicted=pred;
run;
The LOGISTIC Procedure
Model Information
Data Set WORK.LOWBWT31
Response Variable LOW < 2500g
Number of Response Levels 2
Number of Observations 189
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value LOW Frequency
1 1 59
2 0 130
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 236.672 229.140
SC 239.914 242.107
-2 Log L 234.672 221.140
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 13.5321 3 0.0036
Score 13.3565 3 0.0039
Wald 12.3553 3 0.0063
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 0.7745 0.9101 0.7241 0.3948
lwd 1 -1.9440 1.7248 1.2704 0.2597
AGE 1 -0.0796 0.0396 4.0305 0.0447
lwd*AGE 1 0.1322 0.0757 3.0497 0.0808
Association of Predicted Probabilities and Observed Responses
Percent Concordant 64.3 Somers' D 0.317
Percent Discordant 32.6 Gamma 0.327
Percent Tied 3.1 Tau-a 0.137
Pairs 7670 c 0.659
proc logistic data=lowbwt31 descending;
model low = lwd age;
run;
The LOGISTIC Procedure
Model Information
Data Set WORK.LOWBWT31
Response Variable LOW < 2500g
Number of Response Levels 2
Number of Observations 189
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value LOW Frequency
1 1 59
2 0 130
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 236.672 230.287
SC 239.914 240.012
-2 Log L 234.672 224.287
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 10.3852 2 0.0056
Score 10.6703 2 0.0048
Wald 10.0831 2 0.0065
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -0.0269 0.7621 0.0012 0.9719
lwd 1 1.0101 0.3643 7.6899 0.0056
AGE 1 -0.0442 0.0322 1.8841 0.1699
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
lwd 2.746 1.345 5.607
AGE 0.957 0.898 1.019
Association of Predicted Probabilities and Observed Responses
Percent Concordant 62.8 Somers' D 0.288
Percent Discordant 34.1 Gamma 0.297
Percent Tied 3.1 Tau-a 0.124
Pairs 7670 c 0.644
proc logistic data=lowbwt31 descending;
model low = lwd;
run;
The LOGISTIC Procedure
Model Information
Data Set WORK.LOWBWT31
Response Variable LOW < 2500g
Number of Response Levels 2
Number of Observations 189
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value LOW Frequency
1 1 59
2 0 130
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 236.672 230.241
SC 239.914 236.725
-2 Log L 234.672 226.241
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 8.4308 1 0.0037
Score 8.8727 1 0.0029
Wald 8.4917 1 0.0036
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.0537 0.1884 31.2860 <.0001
lwd 1 1.0536 0.3616 8.4917 0.0036
The LOGISTIC Procedure
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
lwd 2.868 1.412 5.826
Association of Predicted Probabilities and Observed Responses
Percent Concordant 29.8 Somers' D 0.194
Percent Discordant 10.4 Gamma 0.483
Percent Tied 59.8 Tau-a 0.084
Pairs 7670 c 0.597
proc logistic data=lowbwt31 descending;
model low=;
run;
quit;
The LOGISTIC Procedure
Model Information
Data Set WORK.LOWBWT31
Response Variable LOW < 2500g
Number of Response Levels 2
Number of Observations 189
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value LOW Frequency
1 1 59
2 0 130
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
-2 Log L = 234.672
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -0.7900 0.1570 25.3270 <.0001
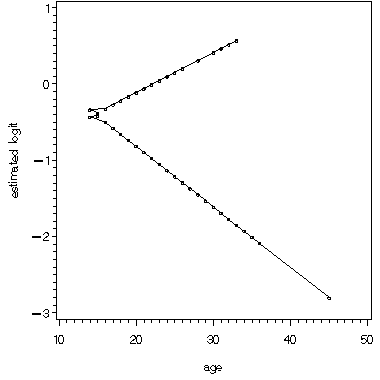
page 78 Figure 3.3 Plot of the estimated logit for women with LWD = 1 and for women with LWD = from Model 3 in Table 3.17.
data lowbwt31;
infile 'D:workdatarawlogisticlowbwt.dat';
input id low age lwt race smoke ptd ht ui ftv bwt;
if race = 1 then do; race2 = 0; race3 = 0; end;
if race = 2 then do; race2 = 1; race3 = 0; end;
if race = 3 then do; race2 = 0; race3 = 1; end;
lwd=(lwt<110);
run;
proc logistic data=lowbwt31 descending;
model low = lwd age lwd*age;
output out=lowbwt32 xbeta=xb;
run;
proc sort data=lowbwt32;
by xb;
run;
symbol1 i=join value=circle;
axis1 label = (a=90 'estimated logit');
axis2 label = ("age");
proc gplot data=lowbwt32;
plot xb*age=1 /vaxis=axis1 haxis = axis2;
run;
quit;
page 78 Table 3.15 Estimated covariance matrix for the estimated parameters in Model 3 of Table 3.14.
proc logistic data=lowbwt31 descending covout outest=lowbwt33;
model low = lwd age lwd*age;
run;
quit;
The LOGISTIC Procedure
Model Information
Data Set WORK.LOWBWT31
Response Variable LOW < 2500g
Number of Response Levels 2
Number of Observations 189
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value LOW Frequency
1 1 59
2 0 130
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 236.672 229.140
SC 239.914 242.107
-2 Log L 234.672 221.140
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 13.5321 3 0.0036
Score 13.3565 3 0.0039
Wald 12.3553 3 0.0063
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 0.7745 0.9101 0.7241 0.3948
lwd 1 -1.9440 1.7248 1.2704 0.2597
AGE 1 -0.0796 0.0396 4.0305 0.0447
lwd*AGE 1 0.1322 0.0757 3.0497 0.0808
Association of Predicted Probabilities and Observed Responses
Percent Concordant 64.3 Somers' D 0.317
Percent Discordant 32.6 Gamma 0.327
Percent Tied 3.1 Tau-a 0.137
Pairs 7670 c 0.659
proc print data=lowbwt33;
where _type_='COV';
var _name_ intercept lwd age lwdage;
run;
Obs _NAME_ Intercept lwd AGE lwdAGE
2 Intercept 0.82827 -0.82827 -0.035266 0.03527
3 lwd -0.82827 2.97495 0.035266 -0.12760
4 AGE -0.03527 0.03527 0.001571 -0.00157
5 lwdAGE 0.03527 -0.12760 -0.001571 0.00573
page 79 Table 3.16 Estimated odds ratios and 95% confidence intervals for LWD, controlling for AGE.
proc genmod data=lowbwt32 descending;
model low = lwd age lwd*age / dist=bin link=logit waldci;
estimate "age = 15" lwd 1 lwd*age 15 /exp;
estimate "age = 20" lwd 1 lwd*age 20 /exp;
estimate "age = 25" lwd 1 lwd*age 25 /exp;
estimate "age = 30" lwd 1 lwd*age 30 /exp;
run;
The GENMOD Procedure
Model Information
Data Set WORK.LOWBWT32 Predicted Values and
Diagnostic Statistics
Distribution Binomial
Link Function Logit
Dependent Variable LOW < 2500g
Observations Used 189
Probability Modeled Pr( LOW = 1 )
Response Profile
Ordered Ordered
Level Value Count
1 0 130
2 1 59
Parameter Information
Parameter Effect
Prm1 Intercept
Prm2 lwd
Prm3 AGE
Prm4 lwd*AGE
Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF
Deviance 185 221.1399 1.1954
Scaled Deviance 185 221.1399 1.1954
Pearson Chi-Square 185 187.7843 1.0151
Scaled Pearson X2 185 187.7843 1.0151
Log Likelihood -110.5700
Algorithm converged.
Analysis Of Parameter Estimates
Standard Wald 95% Confidence Chi-
Parameter DF Estimate Error Limits Square Pr > ChiSq
Intercept 1 0.7745 0.9101 -1.0093 2.5583 0.72 0.3948
lwd 1 -1.9441 1.7248 -5.3246 1.4365 1.27 0.2597
AGE 1 -0.0796 0.0396 -0.1573 -0.0019 4.03 0.0447
The GENMOD Procedure
Analysis Of Parameter Estimates
Standard Wald 95% Confidence Chi-
Parameter DF Estimate Error Limits Square Pr > ChiSq
lwd*AGE 1 0.1322 0.0757 -0.0162 0.2806 3.05 0.0807
Scale 0 1.0000 0.0000 1.0000 1.0000
NOTE: The scale parameter was held fixed.
Contrast Estimate Results
Standard Chi-
Label Estimate Error Alpha Confidence Limits Square Pr > ChiSq
age = 15 0.0389 0.6604 0.05 -1.2555 1.3332 0.00 0.9531
Exp(age = 15) 1.0396 0.6866 0.05 0.2849 3.7933
age = 20 0.6998 0.4036 0.05 -0.0912 1.4909 3.01 0.0829
Exp(age = 20) 2.0134 0.8126 0.05 0.9128 4.4411
age = 25 1.3608 0.4197 0.05 0.5382 2.1835 10.51 0.0012
Exp(age = 25) 3.8994 1.6367 0.05 1.7129 8.8770
age = 30 2.0218 0.6899 0.05 0.6697 3.3740 8.59 0.0034
Exp(age = 30) 7.5520 5.2100 0.05 1.9536 29.1940
3.8 A comparison of logistic regression and stratified analysis of 2 x 2 tables
page 80 Table 3.17 Cross-classification of low birth weight by smoking status.
proc freq data=lowbwt32;
tables low*smoke;
run;
The FREQ Procedure
Table of LOW by SMOKE
LOW(< 2500g) SMOKE
Frequency|
Percent |
Row Pct |
Col Pct | 0| 1| Total
---------+--------+--------+
0 | 86 | 44 | 130
| 45.50 | 23.28 | 68.78
| 66.15 | 33.85 |
| 74.78 | 59.46 |
---------+--------+--------+
1 | 29 | 30 | 59
| 15.34 | 15.87 | 31.22
| 49.15 | 50.85 |
| 25.22 | 40.54 |
---------+--------+--------+
Total 115 74 189
60.85 39.15 100.00
page 81 Table 3.18 Cross-classification of low birth weight by smoking status stratified by RACE.
proc freq data=lowbwt32;
tables race*low*smoke;
run;
The FREQ Procedure
Table 1 of LOW by SMOKE
Controlling for RACE=1
LOW(< 2500g) SMOKE
Frequency|
Percent |
Row Pct |
Col Pct | 0| 1| Total
---------+--------+--------+
0 | 40 | 33 | 73
| 41.67 | 34.38 | 76.04
| 54.79 | 45.21 |
| 90.91 | 63.46 |
---------+--------+--------+
1 | 4 | 19 | 23
| 4.17 | 19.79 | 23.96
| 17.39 | 82.61 |
| 9.09 | 36.54 |
---------+--------+--------+
Total 44 52 96
45.83 54.17 100.00
Table 2 of LOW by SMOKE
Controlling for RACE=2
LOW(< 2500g) SMOKE
Frequency|
Percent |
Row Pct |
Col Pct | 0| 1| Total
---------+--------+--------+
0 | 11 | 4 | 15
| 42.31 | 15.38 | 57.69
| 73.33 | 26.67 |
| 68.75 | 40.00 |
---------+--------+--------+
1 | 5 | 6 | 11
| 19.23 | 23.08 | 42.31
| 45.45 | 54.55 |
| 31.25 | 60.00 |
---------+--------+--------+
Total 16 10 26
61.54 38.46 100.00
The FREQ Procedure
Table 3 of LOW by SMOKE
Controlling for RACE=3
LOW(< 2500g) SMOKE
Frequency|
Percent |
Row Pct |
Col Pct | 0| 1| Total
---------+--------+--------+
0 | 35 | 7 | 42
| 52.24 | 10.45 | 62.69
| 83.33 | 16.67 |
| 63.64 | 58.33 |
---------+--------+--------+
1 | 20 | 5 | 25
| 29.85 | 7.46 | 37.31
| 80.00 | 20.00 |
| 36.36 | 41.67 |
---------+--------+--------+
Total 55 12 67
82.09 17.91 100.00
page 82 Table 3.19 Tabulation of the estimated odds ratios, ln(estimated odds ratios), estimated variance of the ln(estimated odds ratios), and the inverse of the estimated variance, w, for smoking status within each stratum of RACE.
NOTE: You need to square the standard error given by SAS to the values on the third row of the table.
data lowbwt34;
set lowbwt31;
race2sm = race2*smoke;
race3sm = race3*smoke;
run;
proc genmod data=lowbwt34 descending;
model low = smoke race2 race3 race2sm race3sm / dist=bin link=logit waldci;
estimate 'White' smoke 1 /exp ;
estimate 'Black' smoke 1 race2sm 1 race3sm 0 / exp ;
estimate 'Other' smoke 1 race2sm 0 race3sm 1 / exp ;
run;
The GENMOD Procedure
Model Information
Data Set WORK.LOWBWT34
Distribution Binomial
Link Function Logit
Dependent Variable LOW < 2500g
Observations Used 189
Probability Modeled Pr( LOW = 1 )
Response Profile
Ordered Ordered
Level Value Count
1 0 130
2 1 59
Parameter Information
Parameter Effect
Prm1 Intercept
Prm2 SMOKE
Prm3 race2
Prm4 race3
Prm5 race2sm
Prm6 race3sm
Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF
Deviance 183 216.8178 1.1848
Scaled Deviance 183 216.8178 1.1848
Pearson Chi-Square 183 188.9999 1.0328
Scaled Pearson X2 183 188.9999 1.0328
Log Likelihood -108.4089
Algorithm converged.
Analysis Of Parameter Estimates
Standard Wald 95% Confidence Chi-
Parameter DF Estimate Error Limits Square Pr > ChiSq
Intercept 1 -2.3026 0.5244 -3.3304 -1.2748 19.28 <.0001
SMOKE 1 1.7505 0.5983 0.5779 2.9231 8.56 0.0034
The GENMOD Procedure
Analysis Of Parameter Estimates
Standard Wald 95% Confidence Chi-
Parameter DF Estimate Error Limits Square Pr > ChiSq
race2 1 1.5141 0.7523 0.0397 2.9885 4.05 0.0441
race3 1 1.7430 0.5946 0.5775 2.9084 8.59 0.0034
race2sm 1 -0.5566 1.0322 -2.5797 1.4666 0.29 0.5897
race3sm 1 -1.5274 0.8828 -3.2577 0.2029 2.99 0.0836
Scale 0 1.0000 0.0000 1.0000 1.0000
NOTE: The scale parameter was held fixed.
Contrast Estimate Results
Standard Chi-
Label Estimate Error Alpha Confidence Limits Square Pr > ChiSq
White 1.7505 0.5983 0.05 0.5779 2.9231 8.56 0.0034
Exp(White) 5.7576 3.4446 0.05 1.7823 18.5991
Black 1.1939 0.8412 0.05 -0.4548 2.8426 2.01 0.1558
Exp(Black) 3.3000 2.7759 0.05 0.6346 17.1602
Other 0.2231 0.6492 0.05 -1.0492 1.4955 0.12 0.7310
Exp(Other) 1.2500 0.8115 0.05 0.3502 4.4616
page 84 Table 3.20 Estimated logistic regression coefficients for the variable SMOKE, log-likelihood, the likelihood ratio test statistic (G), and the resulting p-value for estimation of the stratified odds ratio and assessment of homogeneity of odds ratios across strata defined by RACE.
NOTE: SAS give the -2 log likelihood while the text gives the log likelihood. Therefore, you need to divide the value given by SAS by -2 (don't forget to use the -2 log likelihood for both the intercept and the covariates. To get the values of G, you need to subtract the -2 log likelihoods.
proc logistic data=lowbwt34 desc;
model low = smoke / clparm=wald;
run;
The LOGISTIC Procedure
Model Information
Data Set WORK.LOWBWT34
Response Variable LOW < 2500g
Number of Response Levels 2
Number of Observations 189
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value LOW Frequency
1 1 59
2 0 130
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 236.672 233.805
SC 239.914 240.288
-2 Log L 234.672 229.805
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 4.8674 1 0.0274
Score 4.9237 1 0.0265
Wald 4.8516 1 0.0276
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.0870 0.2147 25.6244 <.0001
SMOKE 1 0.7040 0.3196 4.8516 0.0276
The LOGISTIC Procedure
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
SMOKE 2.022 1.081 3.783
Association of Predicted Probabilities and Observed Responses
Percent Concordant 33.6 Somers' D 0.170
Percent Discordant 16.6 Gamma 0.338
Percent Tied 49.7 Tau-a 0.073
Pairs 7670 c 0.585
Wald Confidence Interval for Parameters
Parameter Estimate 95% Confidence Limits
Intercept -1.0870 -1.5078 -0.6661
SMOKE 0.7040 0.0776 1.3305
proc logistic data=lowbwt34 desc;
model low = smoke race2 race3 / clparm=wald;
run;
The LOGISTIC Procedure
Model Information
Data Set WORK.LOWBWT34
Response Variable LOW < 2500g
Number of Response Levels 2
Number of Observations 189
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value LOW Frequency
1 1 59
2 0 130
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 236.672 227.975
SC 239.914 240.942
-2 Log L 234.672 219.975
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 14.6973 3 0.0021
Score 14.1265 3 0.0027
Wald 12.8812 3 0.0049
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.8405 0.3529 27.2065 <.0001
SMOKE 1 1.1160 0.3692 9.1357 0.0025
race2 1 1.0841 0.4900 4.8951 0.0269
race3 1 1.1086 0.4003 7.6689 0.0056
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
SMOKE 3.053 1.480 6.294
race2 2.957 1.132 7.725
race3 3.030 1.383 6.640
Association of Predicted Probabilities and Observed Responses
Percent Concordant 54.5 Somers' D 0.299
Percent Discordant 24.6 Gamma 0.378
Percent Tied 20.9 Tau-a 0.129
Pairs 7670 c 0.650
Wald Confidence Interval for Parameters
Parameter Estimate 95% Confidence Limits
Intercept -1.8405 -2.5321 -1.1489
SMOKE 1.1160 0.3923 1.8397
race2 1.0841 0.1237 2.0444
race3 1.1086 0.3240 1.8931
proc logistic data=lowbwt34 desc;
model low = smoke race2 race3 race2sm race3sm / clparm=wald;
run;
quit;
The LOGISTIC Procedure
Model Information
Data Set WORK.LOWBWT34
Response Variable LOW < 2500g
Number of Response Levels 2
Number of Observations 189
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value LOW Frequency
1 1 59
2 0 130
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 236.672 228.818
SC 239.914 248.268
-2 Log L 234.672 216.818
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 17.8542 5 0.0031
Score 15.8649 5 0.0072
Wald 13.1634 5 0.0219
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
>Intercept 1 -2.3026 0.5244 19.2796 <.0001
SMOKE 1 1.7505 0.5983 8.5611 0.0034
race2 1 1.5141 0.7523 4.0511 0.0441
race3 1 1.7430 0.5946 8.5921 0.0034
race2sm 1 -0.5566 1.0322 0.2907 0.5897
race3sm 1 -1.5274 0.8828 2.9933 0.0836
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
SMOKE 5.758 1.782 18.599
race2 4.545 1.041 19.857
race3 5.714 1.782 18.327
race2sm 0.573 0.076 4.334
race3sm 0.217 0.038 1.225
Association of Predicted Probabilities and Observed Responses
Percent Concordant 54.8 Somers' D 0.305
Percent Discordant 24.3 Gamma 0.386
Percent Tied 20.9 Tau-a 0.132
Pairs 7670 c 0.653
Wald Confidence Interval for Parameters
Parameter Estimate 95% Confidence Limits
Intercept -2.3026 -3.3304 -1.2748
SMOKE 1.7505 0.5779 2.9231
race2 1.5141 0.0397 2.9885
race3 1.7430 0.5775 2.9084
race2sm -0.5566 -2.5797 1.4666
race3sm -1.5274 -3.2577 0.2029
3.9 Interpretation of the fitted values
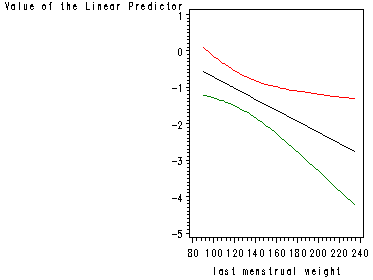
page 86 Figure 3.4 Graph of the estimated logit of low birth weight and 95 percent confidence intervals as a function of weight at the last menstrual period for white women.
proc logistic data=lowbwt34 desc;
model low = lwt race2 race3;
output out=lowbwt35 xbeta=p stdxbeta=sepl;
run;
The LOGISTIC Procedure
Model Information
Data Set WORK.LOWBWT34
Response Variable LOW < 2500g
Number of Response Levels 2
Number of Observations 189
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value LOW Frequency
1 1 59
2 0 130
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 236.672 231.259
SC 239.914 244.226
-2 Log L 234.672 223.259
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 11.4129 3 0.0097
Score 10.7572 3 0.0131
Wald 10.1316 3 0.0175
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 0.8057 0.8452 0.9088 0.3404
LWT 1 -0.0152 0.00644 5.5886 0.0181
race2 1 1.0811 0.4881 4.9065 0.0268
race3 1 0.4806 0.3567 1.8156 0.1778
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
LWT 0.985 0.973 0.997
race2 2.948 1.133 7.672
race3 1.617 0.804 3.253
Association of Predicted Probabilities and Observed Responses
Percent Concordant 64.1 Somers' D 0.293
Percent Discordant 34.8 Gamma 0.296
Percent Tied 1.1 Tau-a 0.127
Pairs 7670 c 0.647
data lowbwt36;
set lowbwt35;
lower = p -1.96*sepl;
upper = p+ 1.96*sepl;
run;
proc sort data=lowbwt36;
by lwt;
run;
symbol1 i=join value=none;
proc gplot data=lowbwt36;
plot p*lwt upper*lwt lower*lwt / overlay;
where race = 1;
run;
quit;
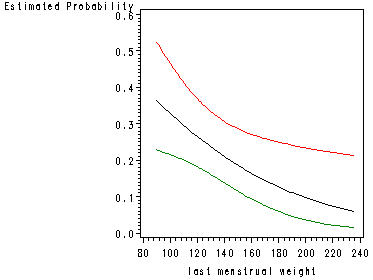
page 87 Figure 3.5 Graph of the estimated probability of low weight birth and 95 percent confidence intervals as a function of weight at the last menstrual period for white women.
proc logistic data=lowbwt34 desc;
model low = lwt race2 race3;
output out=lowbwt37 p=p u=u l=l;
run;
The LOGISTIC Procedure
Model Information
Data Set WORK.LOWBWT34
Response Variable LOW < 2500g
Number of Response Levels 2
Number of Observations 189
Link Function Logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value LOW Frequency
1 1 59
2 0 130
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 236.672 231.259
SC 239.914 244.226
-2 Log L 234.672 223.259
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 11.4129 3 0.0097
Score 10.7572 3 0.0131
Wald 10.1316 3 0.0175
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 0.8057 0.8452 0.9088 0.3404
LWT 1 -0.0152 0.00644 5.5886 0.0181
race2 1 1.0811 0.4881 4.9065 0.0268
race3 1 0.4806 0.3567 1.8156 0.1778
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
LWT 0.985 0.973 0.997
race2 2.948 1.133 7.672
race3 1.617 0.804 3.253
Association of Predicted Probabilities and Observed Responses
Percent Concordant 64.1 Somers' D 0.293
Percent Discordant 34.8 Gamma 0.296
Percent Tied 1.1 Tau-a 0.127
Pairs 7670 c 0.647
proc sort data=lowbwt37;
by lwt;
run;
symbol1 i=join value=none;
proc gplot data=lowbwt37;
plot p*lwt u*lwt l*lwt / overlay;
where race = 1;
run;
quit;