Inputting Blood Pressure data (page 407, Table 10.1).
data ch10tab01;
input x y;
label x='age'
y='Dbp';
cards;
27 73
21 66
22 63
24 75
25 71
23 70
20 65
20 70
29 79
24 72
25 68
28 67
26 79
38 91
32 76
33 69
31 66
34 73
37 78
38 87
33 76
35 79
30 73
31 80
37 68
39 75
46 89
49 101
40 70
42 72
43 80
46 83
43 75
44 71
46 80
47 96
45 92
49 80
48 70
40 90
42 85
55 76
54 71
57 99
52 86
53 79
56 92
52 85
50 71
59 90
50 91
52 100
58 80
57 109
;;;
run;
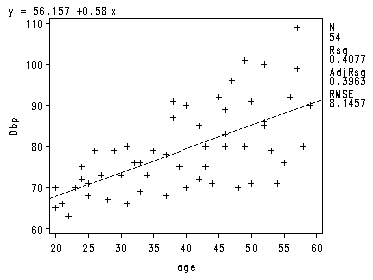
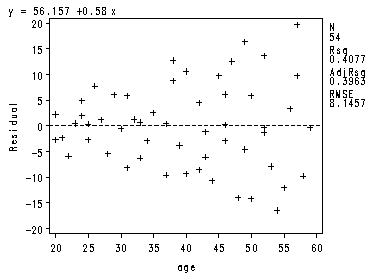
Three Diagnostic Plots Fig. 10.1a and 10.1b, p. 406.
proc reg data=ch10tab01; model y = x; output out=temp r=residual; plot y*x r.*x; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: y DbpAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 1 2374.96833 2374.96833 35.79 <.0001 Error 52 3450.36501 66.35317 Corrected Total 53 5825.33333
Root MSE 8.14575 R-Square 0.4077 Dependent Mean 79.11111 Adj R-Sq 0.3963 Coeff Var 10.29659
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 56.15693 3.99367 14.06 <.0001 x age 1 0.58003 0.09695 5.98 <.0001
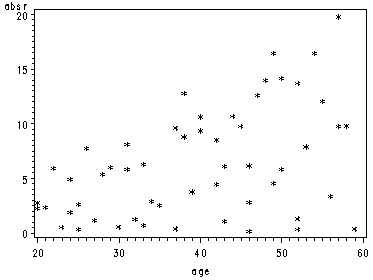
Fig. 10.1c, p. 406.
data temp; set temp; absr = abs(residual); run; symbol1 v=star h=.8; axis1 order=(0 to 20 by 5); proc gplot data = temp; plot absr*x/ vaxis = axis1; run; quit;
Regressing the absolute residuals against X, formula 10.19 page 406.
proc reg data = temp ; model absr = x; output out = temp1 p = s ; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: absrAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 1 277.23091 277.23091 13.93 0.0005 Error 52 1034.62880 19.89671 Corrected Total 53 1311.85971
Root MSE 4.46057 R-Square 0.2113 Dependent Mean 6.29301 Adj R-Sq 0.1962 Coeff Var 70.88141
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 -1.54948 2.18692 -0.71 0.4818 x age 1 0.19817 0.05309 3.73 0.0005
Obtaining the weights, w = 1/(s^2).
Table 10.1, p. 407.
data temp1; set temp1; w = 1/(s**2); run; proc print data = temp1 (obs = 10); run;
Obs x y residual absr s w1 27 73 1.18224 1.18224 3.80117 0.06921 2 21 66 -2.33758 2.33758 2.61214 0.14656 3 22 63 -5.91761 5.91761 2.81031 0.12662 4 24 75 4.92233 4.92233 3.20666 0.09725 5 25 71 0.34230 0.34230 3.40483 0.08626 6 23 70 0.50236 0.50236 3.00849 0.11049 7 20 65 -2.75755 2.75755 2.41397 0.17161 8 20 70 2.24245 2.24245 2.41397 0.17161 9 29 79 6.02218 6.02218 4.19752 0.05676 10 24 72 1.92233 1.92233 3.20666 0.09725
The equation (10.20) by using WLS regression. The option clb in the model statement supplies the confidence interval for the parameters.
proc reg data = temp1; weight w; model y = x / clb; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: y DbpWeight: w
Analysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 1 83.34082 83.34082 56.64 <.0001 Error 52 76.51351 1.47141 Corrected Total 53 159.85432
Root MSE 1.21302 R-Square 0.5214 Dependent Mean 73.55134 Adj R-Sq 0.5122 Coeff Var 1.64921
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t| 95% Confidence Limits
Intercept Intercept 1 55.56577 2.52092 22.04 <.0001 50.50718 60.62436 x age 1 0.59634 0.07924 7.53 <.0001 0.43734 0.75534
Inputting data for Ridge Regression example, p. 413.
data ch7tab01;
input X1 X2 X3 Y;
label x1 = 'Triceps'
x2 = 'Thigh cir.'
x3 = 'Midarm cir.'
y = 'body fat';
cards;
19.5 43.1 29.1 11.9
24.7 49.8 28.2 22.8
30.7 51.9 37.0 18.7
29.8 54.3 31.1 20.1
19.1 42.2 30.9 12.9
25.6 53.9 23.7 21.7
31.4 58.5 27.6 27.1
27.9 52.1 30.6 25.4
22.1 49.9 23.2 21.3
25.5 53.5 24.8 19.3
31.1 56.6 30.0 25.4
30.4 56.7 28.3 27.2
18.7 46.5 23.0 11.7
19.7 44.2 28.6 17.8
14.6 42.7 21.3 12.8
29.5 54.4 30.1 23.9
27.7 55.3 25.7 22.6
30.2 58.6 24.6 25.4
22.7 48.2 27.1 14.8
25.2 51.0 27.5 21.1
;
run;
Transforming the variables using the correlation transformation (7.44).
proc sql;
create table ch7tab1a as
select *, ( y - mean(y) )/( std(y)*( sqrt( count(y)-1 ) ) ) as ty,
( x1 - mean(x1) )/( std(x1)*( sqrt( count(x1)-1 ) ) ) as tx1,
( x2 - mean(x2) )/( std(x2)*( sqrt( count(x2)-1 ) ) ) as tx2,
( x3 - mean(x3) )/( std(x3)*( sqrt( count(x3)-1 ) ) ) as tx3
from ch7tab01;
quit;
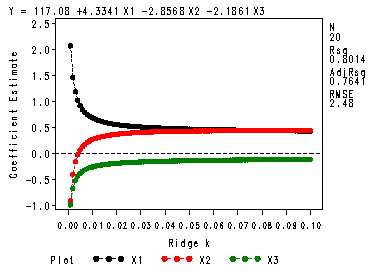
Ridge Regression on Body fat data.
Fig. 10.3, p. 413.
symbol1 v=dot h=.8; proc reg data = ch7tab1a outest = temp outstb noprint; model y = x1-x3/ ridge = (0.001 to 0.1 by .001) outvif ; plot / ridgeplot vref=0; run; quit;
The equations at the bottom of p. 413. The first line are the coefficients for the original variables and the second line are the coefficients for the transformed variables. The transformation shown in (7.44) is done automatically by SAS so there is no need to manually transform the variables yourself. Notice that we used the untransformed variables in the regression models!
proc reg data = ch7tab1a outest = temp outstb noprint; model y = x1-x3 / ridge = 0.02; run; quit; proc print data = temp; where _ridge_ = 0.02 and y = -1; var y intercept x1 x2 x3; run;
Obs Y Intercept X1 X2 X32 -1 -7.40343 0.55535 0.36814 -0.19163 3 -1 0.00000 0.54633 0.37740 -0.13687
Table 10.2, p. 414.
The outstb option in the proc statement tells SAS to put the parameter estimates in the output temp1. These can then be chosen by specifying RIDGESTB in the where statement of the proc print.
proc reg data = ch7tab1a outest = temp outstb outvif; model y = x1-x3/ridge = (0.0 to 0.01 by 0.002 0.02 to 0.05 by 0.01 0.5 1.0); run;quit; proc print data = temp; where _type_ = 'RIDGESTB'; var _ridge_ x1 x2 x3; run;
The REG Procedure Model: MODEL1 Dependent Variable: Y body fatAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 3 396.98461 132.32820 21.52 <.0001 Error 16 98.40489 6.15031 Corrected Total 19 495.38950
Root MSE 2.47998 R-Square 0.8014 Dependent Mean 20.19500 Adj R-Sq 0.7641 Coeff Var 12.28017
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 117.08469 99.78240 1.17 0.2578 X1 Triceps 1 4.33409 3.01551 1.44 0.1699 X2 Thigh cir. 1 -2.85685 2.58202 -1.11 0.2849 X3 Midarm cir. 1 -2.18606 1.59550 -1.37 0.1896 Obs _RIDGE_ X1 X2 X3
4 0.000 4.26370 -2.92870 -1.56142 7 0.002 1.44066 -0.41129 -0.48127 10 0.004 1.00632 -0.02484 -0.31487 13 0.006 0.83002 0.13142 -0.24716 16 0.008 0.73433 0.21576 -0.21030 19 0.010 0.67417 0.26841 -0.18703 22 0.020 0.54633 0.37740 -0.13687 25 0.030 0.50038 0.41341 -0.11808 28 0.040 0.47600 0.43024 -0.10758 31 0.050 0.46046 0.43924 -0.10051 34 0.500 0.33772 0.37906 -0.02950 37 1.000 0.27977 0.31007 -0.00594
Table 10.3, p. 414.
The outvif option in the proc statement of the regression tells SAS to put the VIF’s in the output temp1. These can then be chosen by specifying RIDGEVIF in the where statement of the proc print.
proc print data = temp; where _type_ = 'RIDGEVIF'; var _ridge_ x1 x2 x3; run;
Obs _RIDGE_ X1 X2 X32 0.000 708.843 564.343 104.606 5 0.002 50.559 40.448 8.280 8 0.004 16.982 13.725 3.363 11 0.006 8.503 6.976 2.119 14 0.008 5.147 4.305 1.624 17 0.010 3.486 2.981 1.377 20 0.020 1.103 1.081 1.011 23 0.030 0.626 0.697 0.923 26 0.040 0.453 0.555 0.881 29 0.050 0.370 0.486 0.853 32 0.500 0.154 0.214 0.403 35 1.000 0.107 0.136 0.227
Inputting the Mathematics Proficiency Data, Table 10.4, p. 421.
Note: The easiest method of including observations with multiple words in one string variable is to connect the words with an underscore.
data ch10tab11;
input state $ y x1 x2 x3 x4 x5;
label y = 'Math profeciency'
x1 = 'Parents'
x2 = 'Homelib'
x3 = 'Reading'
x4 = 'TV Watching'
x5 = 'Absences';
cards;
Alabama 252 75 78 34 18 18
Arizona 259 75 73 41 12 26
Arkansas 256 77 77 28 20 23
California 256 78 68 42 11 28
Colorado 267 78 85 38 9 25
Connecticut 270 79 86 43 12 22
Delaware 261 75 83 32 18 28
Distric_of_Columbia 231 47 76 24 33 37
Florida 255 75 73 31 19 27
Georgia 258 73 80 36 17 22
Guam 231 81 64 32 20 28
Hawaii 251 78 69 36 23 26
Idaho 272 84 84 48 7 21
Illinois 260 78 82 43 14 21
Indiana 267 81 84 37 11 23
Iowa 278 83 88 43 8 20
Kentucky 256 79 78 36 14 23
Louisiana 246 73 76 36 19 27
Maryland 260 75 83 34 19 27
Michigan 264 77 84 31 14 25
Minnesota 276 83 88 36 7 20
Montana 280 83 88 44 6 21
Nebraska 276 85 88 42 9 19
New_Hampshire 273 83 88 40 7 22
New_Jersey 269 79 84 41 13 23
New_Mexico 256 77 72 40 11 27
New_York 261 76 79 35 17 29
North_Carolina 250 74 78 37 21 25
North_Dakota 281 85 90 41 6 14
Ohio 264 79 84 36 11 22
Oklahoma 263 78 78 37 14 22
Oregon 271 81 82 41 9 31
Pennsylvania 266 80 86 34 10 24
Rhode_Island 260 78 80 38 12 28
Texas 258 77 70 34 15 18
Virgin_Islands 218 63 76 23 27 22
Virginia 264 78 82 33 16 24
West_Virginia 256 82 80 36 16 25
Wisconsin 274 81 86 38 8 21
Wyoming 272 85 86 43 7 23
;
run;
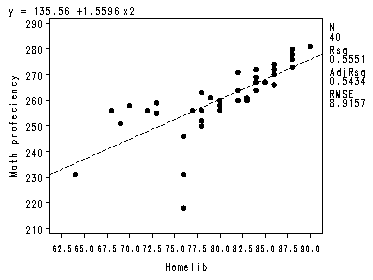
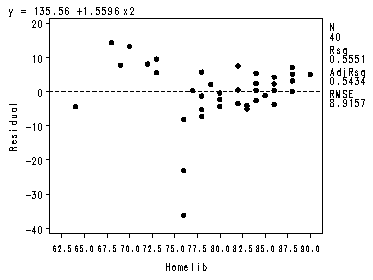
Fig. 10.5, p. 421.
proc reg data = ch10tab11; model y = x2; plot y*x2 r.*x2; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: y Math profeciencyAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 1 3769.30965 3769.30965 47.42 <.0001 Error 38 3020.59035 79.48922 Corrected Total 39 6789.90000
Root MSE 8.91567 R-Square 0.5551 Dependent Mean 260.95000 Adj R-Sq 0.5434 Coeff Var 3.41662
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 135.55589 18.26408 7.42 <.0001 x2 Homelib 1 1.55963 0.22649 6.89 <.0001
The model using robust regression. Invoking the macro robust_hubert which in turn invokes the mad macro. It will create two pictures but this can be modified. We show the Predicted by Residual below.
%include 'c:neter/sas/examples/alsm/mad.sas'; %include 'c:neter/sas/examples/alsm/robust_hubert.sas'; %robust_hubert(ch10tab11, y, x2, 0.000005, 8);
Below you can see the results of the OLS fit (10.49, page 422) followed by the iterations of the reweighted least squares (see table 10.5, page 422) and then the final results (see 10.51, page 423).
The REG Procedure Model: MODEL1 Dependent Variable: y Math profeciencyAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 1 3769.30965 3769.30965 47.42 <.0001 Error 38 3020.59035 79.48922 Corrected Total 39 6789.90000
Root MSE 8.91567 R-Square 0.5551 Dependent Mean 260.95000 Adj R-Sq 0.5434 Coeff Var 3.41662
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 135.55589 18.26408 7.42 <.0001 x2 Homelib 1 1.55963 0.22649 6.89 <.0001 Obs r u _w2_
1 -5.2069 -0.77336 1.00000 2 9.5912 1.42455 0.94416 3 0.3527 0.05239 1.00000 4 14.3894 2.13719 0.62933 5 -1.1243 -0.16699 1.00000 6 0.3161 0.04695 1.00000 7 -4.0050 -0.59485 1.00000 8 -23.0876 -3.42911 0.39223 9 5.5912 0.83044 1.00000 10 -2.3261 -0.34549 1.00000 Obs r _w2_
1 -6.1773 1.00000 2 8.3454 1.00000 3 -0.6728 1.00000 4 12.8681 0.70085 5 -1.7091 1.00000 6 -0.2136 1.00000 7 -4.7000 1.00000 8 -24.1682 0.37316 9 4.3454 1.00000 10 -3.1864 1.00000 Obs r _w2_
1 -6.3179 1.00000 2 8.1025 1.00000 3 -0.8338 1.00000 4 12.5230 0.70388 5 -1.7065 1.00000 6 -0.1906 1.00000 7 -4.7384 1.00000 8 -24.3498 0.36200 9 4.1025 1.00000 10 -3.2861 1.00000 Obs r _w2_
1 -6.3529 1.00000 2 8.0501 1.00000 3 -0.8723 1.00000 4 12.4531 0.70504 5 -1.7171 1.00000 6 -0.1977 1.00000 7 -4.7559 1.00000 8 -24.3917 0.35995 9 4.0501 1.00000 10 -3.3141 1.00000 Obs r _w2_
1 -6.3602 1.00000 2 8.0389 1.00000 3 -0.8804 1.00000 4 12.4380 0.70527 5 -1.7190 1.00000 6 -0.1988 1.00000 7 -4.7593 1.00000 8 -24.4006 0.35951 9 4.0389 1.00000 10 -3.3198 1.00000 Obs r _w2_
1 -6.3618 1.00000 2 8.0365 1.00000 3 -0.8821 1.00000 4 12.4348 0.70532 5 -1.7194 1.00000 6 -0.1990 1.00000 7 -4.7600 1.00000 8 -24.4025 0.35941 9 4.0365 1.00000 10 -3.3211 1.00000 Obs r _w2_
1 -6.3621 1.00000 2 8.0360 1.00000 3 -0.8825 1.00000 4 12.4341 0.70533 5 -1.7194 1.00000 6 -0.1991 1.00000 7 -4.7602 1.00000 8 -24.4029 0.35939 9 4.0360 1.00000 10 -3.3213 1.00000 Obs r _w2_
1 -6.3622 1.00000 2 8.0359 1.00000 3 -0.8826 1.00000 4 12.4340 0.70533 5 -1.7195 1.00000 6 -0.1991 1.00000 7 -4.7602 1.00000 8 -24.4029 0.35939 9 4.0359 1.00000 10 -3.3214 1.00000
The REG Procedure Model: MODEL1 Dependent Variable: y Math profeciency
Weight: _w2_
Analysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 1 3165.87899 3165.87899 78.49 <.0001 Error 38 1532.63864 40.33260 Corrected Total 39 4698.51763
Root MSE 6.35079 R-Square 0.6738 Dependent Mean 262.40346 Adj R-Sq 0.6652 Coeff Var 2.42024
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 142.95244 13.52182 10.57 <.0001 x2 Homelib 1 1.47961 0.16700 8.86 <.0001
Sections 10.4 and 10.5 were skipped. For help using Loess method please come see us in consulting and for Bootstrapping you might consider using the bs command in Stata, for example https://stats.idre.ucla.edu/stat/stata/examples/ara/arastata16.htm.
Section 10.6–Model Validation!
Inputting the Surgical Unit data, Table 8.1, p. 335.
data ch8tab01;
input x1 x2 x3 x4 y logy;
label x1 = 'blood-clotting'
x2 = 'prognostic'
x3 = 'enzyme'
x4 = 'liver function'
y = 'survival'
logy = 'Logsurvival';
cards;
6.7 62 81 2.59 200 2.3010
5.1 59 66 1.70 101 2.0043
7.4 57 83 2.16 204 2.3096
6.5 73 41 2.01 101 2.0043
7.8 65 115 4.30 509 2.7067
5.8 38 72 1.42 80 1.9031
5.7 46 63 1.91 80 1.9031
3.7 68 81 2.57 127 2.1038
6.0 67 93 2.50 202 2.3054
3.7 76 94 2.40 203 2.3075
6.3 84 83 4.13 329 2.5172
6.7 51 43 1.86 65 1.8129
5.8 96 114 3.95 830 2.9191
5.8 83 88 3.95 330 2.5185
7.7 62 67 3.40 168 2.2253
7.4 74 68 2.40 217 2.3365
6.0 85 28 2.98 87 1.9395
3.7 51 41 1.55 34 1.5315
7.3 68 74 3.56 215 2.3324
5.6 57 87 3.02 172 2.2355
5.2 52 76 2.85 109 2.0374
3.4 83 53 1.12 136 2.1335
6.7 26 68 2.10 70 1.8451
5.8 67 86 3.40 220 2.3424
6.3 59 100 2.95 276 2.4409
5.8 61 73 3.50 144 2.1584
5.2 52 86 2.45 181 2.2577
11.2 76 90 5.59 574 2.7589
5.2 54 56 2.71 72 1.8573
5.8 76 59 2.58 178 2.2504
3.2 64 65 0.74 71 1.8513
8.7 45 23 2.52 58 1.7634
5.0 59 73 3.50 116 2.0645
5.8 72 93 3.30 295 2.4698
5.4 58 70 2.64 115 2.0607
5.3 51 99 2.60 184 2.2648
2.6 74 86 2.05 118 2.0719
4.3 8 119 2.85 120 2.0792
4.8 61 76 2.45 151 2.1790
5.4 52 88 1.81 148 2.1703
5.2 49 72 1.84 95 1.9777
3.6 28 99 1.30 75 1.8751
8.8 86 88 6.40 483 2.6840
6.5 56 77 2.85 153 2.1847
3.4 77 93 1.48 191 2.2810
6.5 40 84 3.00 123 2.0899
4.5 73 106 3.05 311 2.4928
4.8 86 101 4.10 398 2.5999
5.1 67 77 2.86 158 2.1987
3.9 82 103 4.55 310 2.4914
6.6 77 46 1.95 124 2.0934
6.4 85 40 1.21 125 2.0969
6.4 59 85 2.33 198 2.2967
8.8 78 72 3.20 313 2.4955
;
run;
Inputting the Validation dataset, Table 10.10, p. 439.
data ch10tab10;
input x1 x2 x3 x4 logy;
label x1 = 'Clotting'
x2 = 'Prognostic'
x3 = 'Enzyme'
x4 = 'Liver'
logy = 'logSurvival';
cards;
7.1 23 78 1.93 2.0326
4.9 66 91 3.05 2.4086
6.4 90 35 1.06 2.2177
5.7 35 70 2.13 1.9078
6.1 42 69 2.25 2.0035
8.0 27 83 2.03 2.0945
6.8 34 51 1.27 1.7652
4.7 63 36 1.71 1.7925
7.0 47 67 1.60 2.1292
6.7 69 65 2.91 2.2295
6.7 46 78 3.26 2.1524
5.8 60 86 3.11 2.3188
6.7 56 32 1.53 1.9039
6.8 51 58 2.18 2.0508
7.2 95 82 4.68 2.6525
7.4 52 67 3.28 2.2053
5.3 53 62 2.42 1.9246
3.5 58 84 1.74 2.1541
6.8 74 79 2.25 2.4970
4.4 47 49 2.42 1.7237
7.0 66 118 4.69 2.8339
6.7 61 57 3.87 2.1282
5.6 75 103 3.11 2.6884
6.9 58 88 3.46 2.4284
6.2 62 57 1.25 2.0261
4.7 97 27 1.77 2.0843
6.8 69 60 2.90 2.2826
6.0 73 58 1.22 2.2073
5.9 50 62 3.19 2.0443
5.5 88 74 3.21 2.4863
3.8 55 52 1.41 1.9037
4.3 99 83 3.93 2.6647
6.6 48 54 2.94 1.9071
6.2 42 63 1.85 1.9093
5.0 60 105 3.17 2.4389
5.8 62 82 3.18 2.3343
4.7 42 10 0.28 1.3379
5.7 70 59 2.28 2.1996
4.7 64 48 1.30 1.8795
7.8 74 40 2.58 2.1504
2.9 43 32 0.94 1.4330
4.9 72 90 3.51 2.4381
4.6 73 57 2.82 2.1075
5.9 78 70 4.28 2.2843
4.6 69 70 3.17 2.1615
6.1 53 52 1.84 2.0558
5.9 88 98 3.33 2.7249
4.7 66 68 1.80 2.0520
10.4 62 85 4.65 2.6810
5.8 70 64 2.52 2.2604
5.4 64 81 1.36 2.2553
6.9 90 33 2.78 2.1745
7.9 45 55 2.46 2.0224
4.5 68 60 2.07 2.1413
;;;
run;
Table 10.9, p. 438.
proc reg data = ch8tab01 outest = temp; title 'Results from the Model Building Data set'; model logy = x1 x2 x3/press; run; quit; proc print data = temp; var _press_; run; proc reg data = ch10tab10 outest = temp; title 'Results from the Validation Data set'; model logy = x1 x2 x3/ press; run; quit; proc print data = temp; var _press_; run; title ;
Results from the Model Building Data set
The REG Procedure Model: MODEL1 Dependent Variable: logy LogsurvivalAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 3 3.86291 1.28764 586.04 <.0001 Error 50 0.10986 0.00220 Corrected Total 53 3.97277
Root MSE 0.04687 R-Square 0.9723 Dependent Mean 2.20614 Adj R-Sq 0.9707 Coeff Var 2.12470
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 0.48362 0.04263 11.34 <.0001 x1 blood-clotting 1 0.06923 0.00408 16.98 <.0001 x2 prognostic 1 0.00929 0.00038250 24.30 <.0001 x3 enzyme 1 0.00952 0.00030641 31.08 <.0001
Results from the Model Building Data set
Obs _PRESS_1 0.14045
Results from the Validation Data set
The REG Procedure Model: MODEL1 Dependent Variable: logy logSurvivalAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 3 4.62507 1.54169 730.29 <.0001 Error 50 0.10555 0.00211 Corrected Total 53 4.73062
Root MSE 0.04595 R-Square 0.9777 Dependent Mean 2.16466 Adj R-Sq 0.9763 Coeff Var 2.12257
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 0.50082 0.04192 11.95 <.0001 x1 Clotting 1 0.06741 0.00498 13.53 <.0001 x2 Prognostic 1 0.01011 0.00037193 27.18 <.0001 x3 Enzyme 1 0.00974 0.00030225 32.22 <.0001
Results from the Validation Data set
Obs _PRESS_1 0.12125
Case Example–Mathematical Proficiency.
Note: This data has already been input in this program.
Fig. 10.10a, p. 441.
Calling the scatter matrix macro.
%include 'c:neter/sas/examples/alsm/scatter.sas'; %scatter(data = ch10tab11, var= y x1 x2 x3 x4 x5);
<The scatterplot is not shown>
Fig. 10.10b, p. 441.
proc corr data = ch10tab11; var y x1-x5; run;
he CORR Procedure6 Variables: y x1 x2 x3 x4 x5
Simple Statistics
Variable N Mean Std Dev Sum Minimum Maximum Label
y 40 260.95000 13.19470 10438 218.00000 281.00000 Math profeciency x1 40 77.70000 6.49339 3108 47.00000 85.00000 Parents x2 40 80.40000 6.30344 3216 64.00000 90.00000 Homelib x3 40 36.85000 5.26016 1474 23.00000 48.00000 Reading x4 40 14.00000 5.99572 560.00000 6.00000 33.00000 TV Watching x5 40 23.92500 4.07863 957.00000 14.00000 37.00000 Absences
Pearson Correlation Coefficients, N = 40 Prob > |r| under H0: Rho=0
y x1 x2 x3 x4 x5
y 1.00000 0.74141 0.74507 0.71659 -0.87348 -0.48034 Math profeciency <.0001 <.0001 <.0001 <.0001 0.0017
x1 0.74141 1.00000 0.39454 0.69304 -0.83115 -0.56531 Parents <.0001 0.0118 <.0001 <.0001 0.0001
x2 0.74507 0.39454 1.00000 0.37692 -0.59364 -0.44262 Homelib <.0001 0.0118 0.0165 <.0001 0.0042
x3 0.71659 0.69304 0.37692 1.00000 -0.79187 -0.35669 Reading <.0001 <.0001 0.0165 <.0001 0.0239
x4 -0.87348 -0.83115 -0.59364 -0.79187 1.00000 0.51168 TV Watching <.0001 <.0001 <.0001 <.0001 0.0007
x5 -0.48034 -0.56531 -0.44262 -0.35669 0.51168 1.00000 Absences 0.0017 0.0001 0.0042 0.0239 0.0007
Fitted model (10.61) p. 441.
proc reg data = ch10tab11; model y = x1-x5; output out = temp h = hii student=ti cookd = Di; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: y Math profeciencyAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 5 5846.32774 1169.26555 42.13 <.0001 Error 34 943.57226 27.75213 Corrected Total 39 6789.90000
Root MSE 5.26803 R-Square 0.8610 Dependent Mean 260.95000 Adj R-Sq 0.8406 Coeff Var 2.01879
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 155.03039 36.23830 4.28 0.0001 x1 Parents 1 0.39115 0.25709 1.52 0.1374 x2 Homelib 1 0.86387 0.17971 4.81 <.0001 x3 Reading 1 0.36162 0.26896 1.34 0.1877 x4 TV Watching 1 -0.84672 0.35254 -2.40 0.0219 x5 Absences 1 0.19229 0.26361 0.73 0.4707
Table 10.12, p. 442.
proc print data = temp (obs = 10); var hii ti Di; run;
Obs hii ti Di1 0.16014 -0.05464 0.00009 2 0.18531 0.40076 0.00609 3 0.16201 1.39338 0.06256 4 0.29069 0.10337 0.00073 5 0.09541 -0.57826 0.00588 6 0.12133 0.03171 0.00002 7 0.11685 0.64985 0.00931 8 0.69026 1.39145 0.71914 9 0.09109 1.44485 0.03487 10 0.07670 0.48432 0.00325
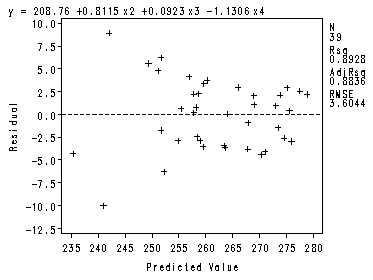
The fitted model using robust regression (10.62), p. 442.
Running the Hubert robust regression.
Running the Hubert/Biweight robust regression which is similar to rreg in Stata.
Invoking two different macros.
Here is the first macro, robust_hubert.
%include 'c:neter/sas/examples/alsm/mad.sas'; %include 'c:neter/sas/examples/alsm/robust_hubert.sas'; %robust_hubert(ch10tab11, y, x2 x3 x4, 0.0005, 9);
The REG Procedure Model: MODEL1 Dependent Variable: y Math profeciencyAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 3 5781.00353 1927.00118 68.76 <.0001 Error 36 1008.89647 28.02490 Corrected Total 39 6789.90000
Root MSE 5.29386 R-Square 0.8514 Dependent Mean 260.95000 Adj R-Sq 0.8390 Coeff Var 2.02869
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 199.61074 21.52892 9.27 <.0001 x2 Homelib 1 0.78043 0.17020 4.59 <.0001 x3 Reading 1 0.40118 0.26876 1.49 0.1442 x4 TV Watching 1 -1.15647 0.27140 -4.26 0.0001 Obs r u _w2_
1 -1.30771 -0.28443 1.00000 2 -0.15269 -0.03321 1.00000 3 8.19275 1.78192 0.75481 4 -0.80821 -0.17578 1.00000 5 -3.78369 -0.82295 1.00000 6 -0.10060 -0.02188 1.00000 7 4.59251 0.99887 1.00000 8 0.61205 0.13312 1.00000 9 7.95444 1.73008 0.77742 10 1.17259 0.25504 1.00000 Obs r _w2_
1 -1.97842 1.00000 2 0.70596 1.00000 3 6.47543 0.92592 4 0.45509 1.00000 5 -3.93974 1.00000 6 0.55384 1.00000 7 3.35113 1.00000 8 -1.92494 1.00000 9 6.95415 0.86218 10 0.78291 1.00000 Obs r _w2_
1 -2.16585 1.00000 2 0.68042 1.00000 3 6.05663 0.99024 4 0.40731 1.00000 5 -4.00323 1.00000 6 0.74252 1.00000 7 3.13259 1.00000 8 -2.35721 1.00000 9 6.60526 0.90799 10 0.68544 1.00000 Obs r _w2_
1 -2.24010 1.00000 2 0.60703 1.00000 3 5.90929 1.00000 4 0.29252 1.00000 5 -4.02355 1.00000 6 0.81795 1.00000 7 3.07963 1.00000 8 -2.47327 1.00000 9 6.45193 0.93764 10 0.64893 1.00000 Obs r _w2_
1 -2.26999 1.00000 2 0.55502 1.00000 3 5.85944 1.00000 4 0.21310 1.00000 5 -4.02818 1.00000 6 0.84502 1.00000 7 3.07071 1.00000 8 -2.50289 1.00000 9 6.38705 0.94683 10 0.63394 1.00000 Obs r _w2_
1 -2.28228 1.00000 2 0.53287 1.00000 3 5.83868 1.00000 4 0.17892 1.00000 5 -4.02932 1.00000 6 0.85736 1.00000 7 3.06771 1.00000 8 -2.51505 1.00000 9 6.35958 0.95076 10 0.62809 1.00000 Obs r _w2_
1 -2.28754 1.00000 2 0.52337 1.00000 3 5.82983 1.00000 4 0.16428 1.00000 5 -4.02981 1.00000 6 0.86264 1.00000 7 3.06644 1.00000 8 -2.52021 1.00000 9 6.34783 0.95245 10 0.62559 1.00000 Obs r _w2_
1 -2.28978 1.00000 2 0.51931 1.00000 3 5.82603 1.00000 4 0.15802 1.00000 5 -4.03002 1.00000 6 0.86489 1.00000 7 3.06590 1.00000 8 -2.52242 1.00000 9 6.34281 0.95317 10 0.62453 1.00000 Obs r _w2_
1 -2.29074 1.00000 2 0.51758 1.00000 3 5.82441 1.00000 4 0.15534 1.00000 5 -4.03011 1.00000 6 0.86586 1.00000 7 3.06567 1.00000 8 -2.52337 1.00000 9 6.34066 0.95348 10 0.62407 1.00000
The REG Procedure Model: MODEL1 Dependent Variable: y Math profeciency
Weight: _w2_
Analysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 3 4391.06625 1463.68875 83.27 <.0001 Error 36 632.76457 17.57679 Corrected Total 39 5023.83082
Root MSE 4.19247 R-Square 0.8740 Dependent Mean 262.15459 Adj R-Sq 0.8636 Coeff Var 1.59924
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 207.83984 17.58882 11.82 <.0001 x2 Homelib 1 0.79410 0.14083 5.64 <.0001 x3 Reading 1 0.16362 0.22036 0.74 0.4626 x4 TV Watching 1 -1.16953 0.21890 -5.34 <.0001
Here is the second macro, robust_hb.
%include 'c:neter/sas/examples/alsm/robust_hb.sas'; %robust_hb(ch10tab11, y, x2 x3 x4, 0.01, 0.0005, 9);
The REG Procedure Model: MODEL1 Dependent Variable: y Math profeciencyAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 3 5781.00353 1927.00118 68.76 <.0001 Error 36 1008.89647 28.02490 Corrected Total 39 6789.90000
Root MSE 5.29386 R-Square 0.8514 Dependent Mean 260.95000 Adj R-Sq 0.8390 Coeff Var 2.02869
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 199.61074 21.52892 9.27 <.0001 x2 Homelib 1 0.78043 0.17020 4.59 <.0001 x3 Reading 1 0.40118 0.26876 1.49 0.1442 x4 TV Watching 1 -1.15647 0.27140 -4.26 0.0001 Obs r u _w2_
1 -1.30771 -0.28443 1.00000 2 -0.15269 -0.03321 1.00000 3 8.19275 1.78192 0.75481 4 -0.80821 -0.17578 1.00000 5 -3.78369 -0.82295 1.00000 6 -0.10060 -0.02188 1.00000 7 4.59251 0.99887 1.00000 8 0.61205 0.13312 1.00000 9 7.95444 1.73008 0.77742 10 1.17259 0.25504 1.00000 Obs r _w2_
1 -1.97842 1.00000 2 0.70596 1.00000 3 6.47543 0.92592 4 0.45509 1.00000 5 -3.93974 1.00000 6 0.55384 1.00000 7 3.35113 1.00000 8 -1.92494 1.00000 9 6.95415 0.86218 10 0.78291 1.00000 Obs r _w2_
1 -2.16585 1.00000 2 0.68042 1.00000 3 6.05663 0.99024 4 0.40731 1.00000 5 -4.00323 1.00000 6 0.74252 1.00000 7 3.13259 1.00000 8 -2.35721 1.00000 9 6.60526 0.90799 10 0.68544 1.00000 Obs r _w2_
1 -2.24010 1.00000 2 0.60703 1.00000 3 5.90929 1.00000 4 0.29252 1.00000 5 -4.02355 1.00000 6 0.81795 1.00000 7 3.07963 1.00000 8 -2.47327 1.00000 9 6.45193 0.93764 10 0.64893 1.00000 Obs r _w2_
1 -2.26999 1.00000 2 0.55502 1.00000 3 5.85944 1.00000 4 0.21310 1.00000 5 -4.02818 1.00000 6 0.84502 1.00000 7 3.07071 1.00000 8 -2.50289 1.00000 9 6.38705 0.94683 10 0.63394 1.00000 Obs r _w2_
1 -2.28228 1.00000 2 0.53287 1.00000 3 5.83868 1.00000 4 0.17892 1.00000 5 -4.02932 1.00000 6 0.85736 1.00000 7 3.06771 1.00000 8 -2.51505 1.00000 9 6.35958 0.95076 10 0.62809 1.00000 Obs r _w2_
1 -2.28754 1.00000 2 0.52337 1.00000 3 5.82983 1.00000 4 0.16428 1.00000 5 -4.02981 1.00000 6 0.86264 1.00000 7 3.06644 1.00000 8 -2.52021 1.00000 9 6.34783 0.95245 10 0.62559 1.00000 Obs r _w2_
1 -2.28978 0.97649 2 0.51931 0.99878 3 5.82603 0.85279 4 0.15802 0.99989 5 -4.03002 0.92810 6 0.86489 0.99663 7 3.06590 0.95806 8 -2.52242 0.97151 9 6.34281 0.82680 10 0.62453 0.99824 Obs r _w2_
1 -2.73012 0.96699 2 0.86459 0.99666 3 4.96329 0.89302 4 0.72986 0.99762 5 -4.06566 0.92755 6 1.00401 0.99550 7 2.37379 0.97500 8 -4.09078 0.92667 9 5.80575 0.85515 10 0.29495 0.99961 Obs r _w2_
1 -2.81014 0.96404 2 0.83110 0.99683 3 4.83738 0.89535 4 0.68947 0.99782 5 -4.06672 0.92544 6 1.02494 0.99518 7 2.29836 0.97587 8 -4.29038 0.91720 9 5.68803 0.85684 10 0.23689 0.99974 Obs r _w2_
1 -2.83138 0.96315 2 0.80418 0.99700 3 4.80324 0.89581 4 0.64927 0.99804 5 -4.06725 0.92471 6 1.03939 0.99499 7 2.28767 0.97586 8 -4.32471 0.91509 9 5.64737 0.85748 10 0.22449 0.99977 Obs r _w2_
1 -2.83871 0.96282 2 0.79223 0.99708 3 4.79108 0.89594 4 0.63096 0.99815 5 -4.06757 0.92442 6 1.04606 0.99491 7 2.28533 0.97582 8 -4.33367 0.91444 9 5.63172 0.85773 10 0.22075 0.99977 Obs r _w2_
1 -2.84151 0.96269 2 0.78734 0.99711 3 4.78636 0.89600 4 0.62341 0.99819 5 -4.06772 0.92431 6 1.04886 0.99488 7 2.28460 0.97580 8 -4.33669 0.91420 9 5.62552 0.85783 10 0.21941 0.99978 Obs r _w2_
1 -2.84261 0.96264 2 0.78538 0.99712 3 4.78449 0.89602 4 0.62036 0.99820 5 -4.06779 0.92426 6 1.05000 0.99486 7 2.28434 0.97579 8 -4.33783 0.91411 9 5.62305 0.85788 10 0.21890 0.99978 Obs r _w2_
1 -2.84305 0.96262 2 0.78459 0.99713 3 4.78374 0.89602 4 0.61914 0.99821 5 -4.06782 0.92425 6 1.05046 0.99486 7 2.28423 0.97579 8 -4.33828 0.91407 9 5.62206 0.85789 10 0.21869 0.99978
The REG Procedure Model: MODEL1 Dependent Variable: y Math profeciency
Weight: _w2_
Analysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 3 3786.64784 1262.21595 97.16 <.0001 Error 35 454.69842 12.99138 Corrected Total 38 4241.34626
Root MSE 3.60436 R-Square 0.8928 Dependent Mean 262.64784 Adj R-Sq 0.8836 Coeff Var 1.37232
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 208.75986 15.50570 13.46 <.0001 x2 Homelib 1 0.81146 0.12370 6.56 <.0001 x3 Reading 1 0.09235 0.19497 0.47 0.6387 x4 TV Watching 1 -1.13056 0.19267 -5.87 <.0001
Fig. 10.11, p. 443.
proc reg data = ch10tab11; model y = x1-x5/ selection = rsquare best = 2 cp adjrsq ; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: yR-Square Selection Method
Number in Adjusted Model R-Square R-Square C(p) Variables in Model
1 0.7630 0.7567 21.9929 x4 1 0.5551 0.5434 72.8418 x2 ——————————————————————- 2 0.8422 0.8337 4.6039 x2 x4 2 0.7923 0.7810 16.8260 x1 x2 ——————————————————————- 3 0.8514 0.8390 4.3538 x2 x3 x4 3 0.8507 0.8383 4.5237 x1 x2 x4 ——————————————————————- 4 0.8589 0.8427 4.5321 x1 x2 x3 x4 4 0.8536 0.8369 5.8078 x1 x2 x4 x5 ——————————————————————- 5 0.8610 0.8406 6.0000 x1 x2 x3 x4 x5
The model fitted by OLS (10.63), p. 443.
proc reg data = ch10tab11; model y = x2 x3 x4; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: y Math profeciencyAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 3 5781.00353 1927.00118 68.76 <.0001 Error 36 1008.89647 28.02490 Corrected Total 39 6789.90000
Root MSE 5.29386 R-Square 0.8514 Dependent Mean 260.95000 Adj R-Sq 0.8390 Coeff Var 2.02869
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 199.61074 21.52892 9.27 <.0001 x2 Homelib 1 0.78043 0.17020 4.59 <.0001 x3 Reading 1 0.40118 0.26876 1.49 0.1442 x4 TV Watching 1 -1.15647 0.27140 -4.26 0.0001