Inputting the Insurance Innovation Data, Table 11.1, p. 459.
data ch11tab01;
input y x1 x2;
label y = 'Months'
x1 = 'Size'
x2 = 'Firm Indicator';
cards;
17 151 0
26 92 0
21 175 0
30 31 0
22 104 0
0 277 0
12 210 0
19 120 0
4 290 0
16 238 0
28 164 1
15 272 1
11 295 1
38 68 1
31 85 1
21 224 1
20 166 1
13 305 1
30 124 1
14 246 1
;
run;
Table 11.2, p. 459.
proc reg data = ch11tab01; model y = x1 x2/ clb; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: y Months
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 2 1504.41333 752.20667 72.50 <.0001
Error 17 176.38667 10.37569
Corrected Total 19 1680.80000
Root MSE 3.22113 R-Square 0.8951
Dependent Mean 19.40000 Adj R-Sq 0.8827
Coeff Var 16.60377
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 33.87407 1.81386 18.68 <.0001
x1 Size 1 -0.10174 0.00889 -11.44 <.0001
x2 Firm Indicator 1 8.05547 1.45911 5.52 <.0001
Parameter Estimates
Variable Label DF 95% Confidence Limits
Intercept Intercept 1 30.04716 37.70098
x1 Size 1 -0.12050 -0.08298
x2 Firm Indicator 1 4.97703 11.13391
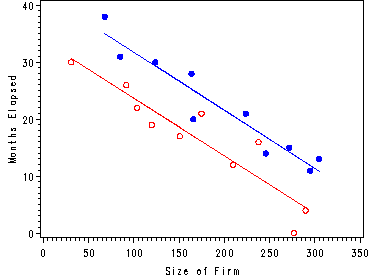
Fig. 11.2, p. 460.
data ch11tab01;
set ch11tab01;
if x2 = 0 then do;
z1 = x1;
y1 = y;
end;
if x2= 1 then do;
z2 = x1 ;
y2 = y;
end;
run;
proc reg data = ch11tab01 noprint;
model y = z1 ;
output out = temp1 p = p1;
run;
proc reg data = temp1 noprint;
model y = z2;
output out=temp p= p2;
run;
quit;
symbol1 c=red v=circle;
symbol2 c=blue v=dot i=none;
symbol3 i=join v=none c=red;
symbol4 i=join v=none c=blue;
axis1 order=(0 to 350 by 50)label=('Size of Firm');
axis2 label=(angle = 90 'Months Elapsed');
proc gplot data = temp;
plot y1*z1 y2*z2 p1*z1 p2*z2 / overlay haxis = axis1 vaxis=axis2;
run;
quit;
Table 11.3, p. 464.
Note: First create the interaction variable and then run the regression.
data ch11tab01; set ch11tab01; x1x2 = x1*x2; run; proc reg data = ch11tab01; model y = x1 x2 x1x2; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: y MonthsAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 3 1504.41904 501.47301 45.49 <.0001 Error 16 176.38096 11.02381 Corrected Total 19 1680.80000
Root MSE 3.32021 R-Square 0.8951 Dependent Mean 19.40000 Adj R-Sq 0.8754 Coeff Var 17.11450
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 33.83837 2.44065 13.86 <.0001 x1 Size 1 -0.10153 0.01305 -7.78 <.0001 x2 Firm Indicator 1 8.13125 3.65405 2.23 0.0408 x1x2 1 -0.00041714 0.01833 -0.02 0.9821
Inputting the Soap Production data, table 11.4, p. 469.
data ch11tab04;
input y x1 x2;
label y = 'Scrap'
x1 = 'Speed'
x2 = 'Production line';
cards;
218 100 1
248 125 1
360 220 1
351 205 1
470 300 1
394 255 1
332 225 1
321 175 1
410 270 1
260 170 1
241 155 1
331 190 1
275 140 1
425 290 1
367 265 1
140 105 0
277 215 0
384 270 0
341 255 0
215 175 0
180 135 0
260 200 0
361 275 0
252 155 0
422 320 0
273 190 0
410 295 0
;
run;
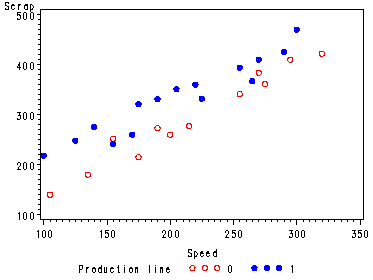
Fig. 11.6, p. 470.
goption reset=all; symbol1 c=red v=circle; symbol2 c=blue v=dot; axis1 order=(100 to 350 by 50); proc gplot data = ch11tab04; plot y*x1 = x2 / haxis = axis1; run; quit;
Table 11.5, p. 471.
The test is the F-test (11.19) p. 472-473. The clb option in the model statement gives us confidence intervals including the CI for beta2 at the bottom of p. 473.
Note1: First create the interaction term, then run the regression.
Note2: The residuals and the fitted values where outputted to be used in Fig. 11.5.
data ch11tab04; set ch11tab04; x1x2 = x1*x2; run; proc reg data = ch11tab04; model y = x1 x2 x1x2/ ss1 clb; output out=temp p=yhat r=residual; test: test x2=x1x2=0; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: y ScrapAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 3 169165 56388 130.95 <.0001 Error 23 9904.05692 430.61117 Corrected Total 26 179069
Root MSE 20.75117 R-Square 0.9447 Dependent Mean 315.48148 Adj R-Sq 0.9375 Coeff Var 6.57762
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t| Type I SS
Intercept Intercept 1 7.57446 20.86970 0.36 0.7200 2687271 x1 Speed 1 1.32205 0.09262 14.27 <.0001 149661 x2 Production line 1 90.39086 28.34573 3.19 0.0041 18694 x1x2 1 -0.17666 0.12884 -1.37 0.1835 809.62258
Parameter Estimates
Variable Label DF 95% Confidence Limits
Intercept Intercept 1 -35.59779 50.74672 x1 Speed 1 1.13044 1.51366 x2 Production line 1 31.75325 149.02848 x1x2 1 -0.44318 0.08986
The REG Procedure Model: MODEL1
Test test Results for Dependent Variable y
Mean Source DF Square F Value Pr > F
Numerator 2 9751.85064 22.65 <.0001 Denominator 23 430.61117
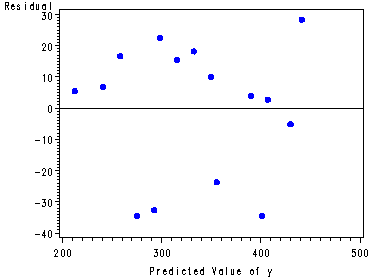
Fig. 11.5a and 11.5b, p. 471.
proc sort data = temp; by x2; run; symbol1 c=blue v=dot; proc gplot data = temp; by x2; plot residual*yhat/ vref = 0; run; quit;
Inputting the Lot Size data, table 11.6, p. 477. Creating the x2 and (x1-500)*x2 variables.
data ch11tab06 ;
input y x1;
label y = 'Cost'
x1 = 'Lot Size';
cards;
2.57 650
4.40 340
4.52 400
1.39 800
4.75 300
3.55 570
2.49 720
3.77 480
;
run;
data ch11tb06a;
set ch11tab06;
x2 = .;
if x1 > 500 then x2 = 1;
else x2 = 0;
x3 = (x1 - 500)*x2;
run;
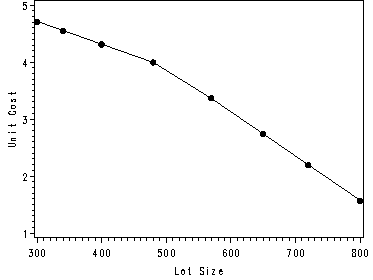
The regression model at the bottom of p. 476.
Note: x3 = (x1-500)*x2.
proc reg data = ch11tb06a; model y = x1 x3; output out=temp p=yhat; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: y CostAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 2 9.48623 4.74311 79.06 0.0002 Error 5 0.29997 0.05999 Corrected Total 7 9.78620
Root MSE 0.24494 R-Square 0.9693 Dependent Mean 3.43000 Adj R-Sq 0.9571 Coeff Var 7.14106
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 5.89545 0.60421 9.76 0.0002 x1 Lot Size 1 -0.00395 0.00149 -2.65 0.0454 x3 1 -0.00389 0.00231 -1.69 0.1528
Fig. 11.9, p. 476.
proc sort data = temp; by x1; run; symbol1 i=join c=black v=dot ; axis1 label=(angle=90 'Unit Cost'); proc gplot data = temp; plot yhat*x1/ vaxis=axis1; run; quit;
Inputting the AADT Data, Table 11.7, p. 484.
data ch11tab07;
input y x1 x2 x3 x4 class truck locale;
cards;
1616 13404 2 52 2 2 5 1
1329 52314 2 60 2 2 5 1
3933 30982 2 57 2 4 5 2
3786 25207 2 64 2 4 5 2
465 20594 2 40 2 2 5 1
794 11507 2 44 2 2 5 1
618 9379 2 43 2 2 5 1
1150 24991 2 42 2 2 5 1
1538 30982 2 59 2 2 5 1
1769 24991 2 41 2 2 5 1
1304 9379 2 30 2 2 5 1
4331 25187 4 52 2 4 5 2
13100 108161 2 48 2 4 5 2
2538 25717 2 24 2 2 5 1
420 14098 2 24 2 2 5 1
429 19871 2 22 2 2 5 1
399 34844 2 22 2 2 5 1
201 14773 2 22 2 2 5 1
587 41722 2 22 2 2 5 1
384 14854 2 24 2 2 5 1
20816 36329 4 24 1 1 1 1
28998 222229 4 24 1 3 1 3
34317 222229 4 26 1 3 1 3
23887 222229 4 24 1 3 1 3
18180 222229 4 24 2 4 2 3
6410 222229 4 24 2 2 2 1
3769 43069 2 24 2 2 2 1
10193 49327 4 24 2 2 1 1
12808 108161 4 24 1 1 1 1
1276 25207 2 20 2 2 4 1
11755 25187 4 24 2 2 2 1
16567 92006 4 24 2 2 2 1
19642 25717 4 24 1 1 1 1
11824 46256 4 24 1 1 1 1
2934 12361 4 24 2 2 2 1
1853 20401 2 24 2 2 1 1
1227 11690 2 24 2 2 2 1
21582 58681 4 24 1 1 1 1
5818 18430 2 20 2 2 5 1
1179 34844 2 24 2 2 2 1
15734 30328 4 24 1 1 1 1
680 34844 2 22 2 2 5 1
877 30982 2 24 2 2 5 1
2795 222229 2 24 2 2 4 1
10647 92006 4 24 2 2 1 1
4933 13043 4 24 2 2 1 1
1193 21050 2 24 2 2 5 1
712 7716 2 24 2 2 2 1
647 12920 2 24 2 2 5 1
2421 43069 2 24 2 2 2 1
1669 14098 2 24 2 2 5 1
1811 14098 2 24 2 2 2 1
1505 13404 2 24 2 2 4 1
2417 21050 2 24 2 2 2 1
1794 20594 2 22 2 2 2 1
429 52314 2 24 2 2 5 1
5697 36329 4 24 1 1 1 1
123665 459784 8 48 1 3 1 3
105844 941411 6 36 1 3 1 3
90807 459784 6 36 1 3 1 3
39799 194279 4 24 1 3 1 2
123445 941411 6 36 1 3 1 3
78343 941411 5 36 1 4 5 3
155547 941411 6 36 1 3 1 3
139309 941411 6 36 1 3 1 2
90594 941411 4 24 1 3 1 2
87003 941411 4 50 1 3 1 3
61617 459784 4 38 1 3 1 3
85393 941411 4 24 1 3 1 3
22165 195998 4 24 1 3 1 2
36977 194279 6 39 1 3 1 2
54941 941411 4 24 1 3 1 2
33272 113571 4 24 1 3 1 2
4348 194279 2 24 2 2 4 1
9025 941411 2 24 2 2 2 1
18574 195998 4 24 2 4 2 2
12665 43784 4 24 2 2 2 1
40642 113571 6 36 1 1 1 1
19341 194279 4 64 2 4 3 2
40602 941411 4 26 2 4 1 2
16550 459784 4 24 2 4 5 2
20240 941411 4 48 2 4 2 2
28793 195998 4 38 2 4 4 2
25114 195998 4 24 2 4 2 2
19007 941411 4 24 2 4 5 2
23557 194279 4 24 2 4 4 2
4860 37046 2 24 2 2 2 1
13823 194279 4 24 2 2 2 1
8972 113571 2 24 2 2 5 1
4307 113571 2 24 2 2 5 1
38857 113571 4 24 2 4 1 1
12230 25717 2 24 2 2 4 1
756 941411 2 24 2 2 5 1
2769 459784 2 44 2 4 5 2
21961 941411 4 28 2 4 5 2
9843 941411 4 44 2 4 5 3
15334 941411 2 24 2 4 5 2
14975 459784 2 24 2 4 5 2
1462 194279 2 24 2 2 5 1
1951 43784 2 22 2 2 5 1
25426 459784 4 19 2 4 5 2
44585 941411 4 28 2 4 5 2
24413 194279 4 26 2 4 5 2
7494 195998 2 25 2 4 5 2
17388 194279 4 48 2 4 5 2
812 194279 2 22 2 2 5 1
3797 43784 2 49 2 4 5 2
4312 113571 2 24 2 2 5 1
1440 113571 2 24 2 2 5 2
12865 459784 2 50 2 4 5 2
5626 459784 2 36 2 4 5 3
3644 459784 2 30 2 4 5 3
8666 195998 4 44 2 4 5 2
3317 37046 2 24 2 4 5 2
4796 194279 2 34 2 4 5 2
5576 194279 2 40 2 4 5 2
13723 941411 2 44 2 4 5 2
21535 941411 4 60 2 4 5 3
14905 459784 4 68 2 4 5 2
15408 459784 2 40 2 4 5 3
1266 43784 2 44 2 4 5 2
;
run;
data ch11tab07;
set ch11tab07;
class1 = 0 ;
if class = 1 then class1 = 1;
class2 = 0;
if class = 2 then class2 = 1;
class3 = 0;
if class = 3 then class3 = 1;
truck1 = 0;
if truck = 1 then truck1 = 1;
truck2 = 0;
if truck = 2 then truck2 = 1;
truck3 = 0;
if truck = 3 then truck3 = 1;
truck4 = 0;
if truck = 4 then truck4 = 1;
locale1 = 0;
if locale = 1 then locale1 = 1;
locale2 = 0;
if locale = 2 then locale2 = 1;
label x1 = 'ctypop'
x2 = 'lanes'
x3 = 'width'
x4 = 'control'
class1 = 'rural int.'
class2 = 'rural nonint.'
class3 = 'urban int.'
locale1 = 'rural'
locale2 = 'urban <= 50000';
run;
Fig. 11.11, p. 485.
We omit the example of the scatterplot matrix.
Initial analysis: regression with all the predictors, residual plot, vif’s, the largest cook’s d.
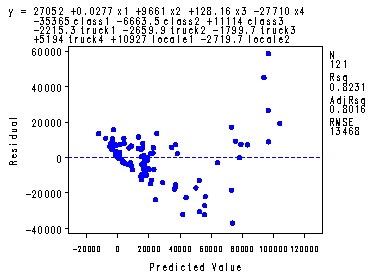
symbol1 v=dot c=blue h=.8; proc reg data = ch11tab07; model y = x1-x4 class1 class2 class3 truck1 truck2 truck3 truck4 locale1 locale2/ vif ; plot r.*p.; output out = temp cookd = cookd; run; quit; proc print data = temp; where cookd > 0.05; var cookd; run;
The REG Procedure Model: MODEL1 Dependent Variable: yAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 13 90306217767 6946632136 38.29 <.0001 Error 107 19409611507 181398238 Corrected Total 120 1.097158E11
Root MSE 13468 R-Square 0.8231 Dependent Mean 19438 Adj R-Sq 0.8016 Coeff Var 69.29022
Parameter Estimates
Parameter Standard Variance Variable Label DF Estimate Error t Value Pr > |t| Inflation
Intercept Intercept 1 27052 29820 0.91 0.3664 0 x1 ctypop 1 0.02771 0.00496 5.58 <.0001 1.76731 x2 lanes 1 9660.98727 1568.49966 6.16 <.0001 2.75058 x3 width 1 128.15518 129.37566 0.99 0.3241 1.47333 x4 control 1 -27710 14571 -1.90 0.0599 24.54914 class1 rural int. 1 -35365 18298 -1.93 0.0559 13.79023 class2 rural nonint. 1 -6663.52080 10181 -0.65 0.5142 17.18991 class3 urban int. 1 11114 15464 0.72 0.4739 20.19940 truck1 1 -2215.34880 6656.19022 -0.33 0.7399 5.74874 truck2 1 -2659.88513 3985.04860 -0.67 0.5059 1.46150 truck3 1 -1799.71245 14179 -0.13 0.8992 1.09908 truck4 1 5193.99138 5555.04832 0.94 0.3519 1.12192 locale1 rural 1 10927 11133 0.98 0.3286 20.60071 locale2 urban <= 50000 1 -2719.67482 4527.06574 -0.60 0.5493 2.98603
Obs cookd
24 0.05619 64 0.15665 65 0.15316 70 0.05289 71 0.09742 91 0.20761 96 0.07146 109 0.20761
Subset selection: based on Rsquare. The include option in the model statement will ensure that all models will include predictors x1 and x2.
proc reg data = ch11tab07;
model y = x1-x4 class1 class2 class3 truck1 truck2 truck3 truck4 locale1 locale2/
selection = rsquare cp best = 5 include=2 start = 3 stop = 7;
run;
quit;
The REG Procedure Model: MODEL1 Dependent Variable: yR-Square Selection Method
NOTE: The variables in the 2 variable model are included in all models.
Number in Model R-Square C(p) Variables in Model
2 0.6946 69.7231 x1 x2 ————————————————————————————————– 3 0.8045 5.2315 class3 3 0.7514 37.3903 x4 3 0.7258 52.8725 truck1 3 0.7045 65.7318 locale2 3 0.7042 65.8798 class1 ————————————————————————————————– 4 0.8121 2.6490 x4 class1 4 0.8104 3.6986 class3 locale2 4 0.8080 5.1275 class3 locale1 4 0.8071 5.6590 class2 class3 4 0.8063 6.1562 class3 truck4 ————————————————————————————————– 5 0.8162 2.1414 x4 class1 locale2 5 0.8158 2.3848 x4 class1 locale1 5 0.8144 3.2803 x4 class1 class2 5 0.8139 3.5589 x4 class1 truck4 5 0.8128 4.2321 x4 class1 truck2 ————————————————————————————————– 6 0.8183 2.8958 x3 x4 class1 locale1 6 0.8180 3.0845 x4 class1 truck4 locale2 6 0.8179 3.1309 x4 class1 truck2 locale2 6 0.8177 3.2367 x4 class1 truck2 locale1 6 0.8177 3.2383 x3 x4 class1 locale2 ————————————————————————————————– 7 0.8204 3.6023 x3 x4 class1 truck4 locale1 7 0.8199 3.9050 x3 x4 class1 truck4 locale2 7 0.8195 4.1891 x3 x4 class1 truck2 locale1 7 0.8192 4.3663 x4 class1 truck2 truck4 locale2 7 0.8190 4.4705 x3 x4 class1 class2 locale1
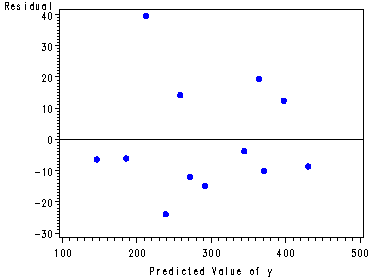
Analyzing the model consisting of the predictors: x1, x2, x4, class1 and class3. If you would like to run proc rsquare this is still possible in SAS v. 8 but it might be hard to find help for this procedure. It might be easier to use the selection = rsquare option in proc reg which will produce the same results.
symbol1 v=dot c=blue h=.8; proc reg data = ch11tab07; model y = x1 x2 x4 class1 class3; plot student.*p.; run; quit;
The Studentized Residual plot is fig. 11.13a, p. 487.
blockquote>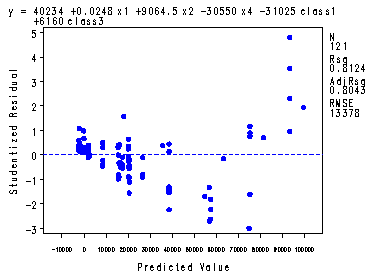
The REG Procedure Model: MODEL1 Dependent Variable: yAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 5 89135575295 17827115059 99.62 <.0001 Error 115 20580253979 178958730 Corrected Total 120 1.097158E11
Root MSE 13378 R-Square 0.8124 Dependent Mean 19438 Adj R-Sq 0.8043 Coeff Var 68.82273
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 40234 28710 1.40 0.1638 x1 ctypop 1 0.02479 0.00436 5.68 <.0001 x2 lanes 1 9064.52332 1329.74878 6.82 <.0001 x4 control 1 -30550 13960 -2.19 0.0307 class1 rural int. 1 -31025 14661 -2.12 0.0365 class3 urban int. 1 6160.03616 13835 0.45 0.6570
Investigating curvilinearity: considering squared terms of x1 and x2, interactions and running the model selection procedure again with all the new variables included.
Note: The variables x1 and x2 should be centered first!
proc means data = ch11tab07;
var x1 x2;
output out=mout mean=mx1 mx2;
run;
data center;
if _n_ = 1 then set mout;
set ch11tab07;
cx1 = x1 - mx1;
cx2 = x2 - mx2;
run;
data center;
set center;
x1sq = cx1**2;
x2sq = cx2**2;
x1x2 = cx1*cx2;
x1x4 = cx1*x4;
x2x4 = cx2*x4;
x1c1 = cx1*class1;
x1c2 = cx1*class2;
x2c1 = cx2*class1;
x2c2 = cx2*class2;
x4c1 = x4*class1;
x4c2 = x4*class2;
run;
proc reg data = center;
model y = x1 x2 x4 class1 class2 x1sq x2sq x1x2 x1x4 x2x4 x1c1 x1c2 x2c1 x2c2 x4c1 x4c2/
selection =rsquare cp include=2 start=3 stop = 7 best = 5;
run;
quit;
The MEANS ProcedureVariable Label N Mean Std Dev Minimum Maximum —————————————————————————————– x1 ctypop 121 263427.67 329469.96 7716.00 941411.00 x2 lanes 121 3.0991736 1.3000318 2.0000000 8.0000000 —————————————————————————————–
The REG Procedure Model: MODEL1 Dependent Variable: y
R-Square Selection Method
NOTE: The variables in the 2 variable model are included in all models.
Number in Model R-Square C(p) Variables in Model
2 0.6946 388.0053 x1 x2 ————————————————————————————————– 3 0.8748 93.2202 x1x4 3 0.8283 169.7793 x2x4 3 0.8203 182.9602 x1x2 3 0.7657 272.9252 x2sq 3 0.7514 296.5162 x4 ————————————————————————————————– 4 0.9231 15.6875 x1x4 x2x4 4 0.9010 52.1299 x2sq x1x4 4 0.8977 57.4939 x4 x1x4 4 0.8857 77.3097 x1x4 x2c2 4 0.8835 80.9151 x1x2 x1x4 ————————————————————————————————– 5 0.9281 9.3483 class2 x1x4 x2x4 5 0.9281 9.3483 x1x4 x2x4 x4c2 5 0.9253 13.9612 x1x2 x1x4 x2x4 5 0.9246 15.2330 x4 x2sq x1x4 5 0.9244 15.4813 x1sq x1x4 x2x4 ————————————————————————————————– 6 0.9313 6.0695 class2 x1x2 x1x4 x2x4 6 0.9313 6.0695 x1x2 x1x4 x2x4 x4c2 6 0.9299 8.4143 class2 x1x4 x2x4 x2c1 6 0.9299 8.4143 x1x4 x2x4 x2c1 x4c2 6 0.9293 9.4977 class2 x1x4 x2x4 x2c2 ————————————————————————————————– 7 0.9331 5.2325 x4 class2 x2sq x1x2 x1x4 7 0.9331 5.2325 x4 x2sq x1x2 x1x4 x4c2 7 0.9324 6.3338 class2 x1x2 x1x4 x2x4 x2c1 7 0.9324 6.3338 x1x2 x1x4 x2x4 x2c1 x4c2 7 0.9322 6.5830 x4 x1sq x2sq x1x2 x1x4
NOTE: Models of not full rank are not included.
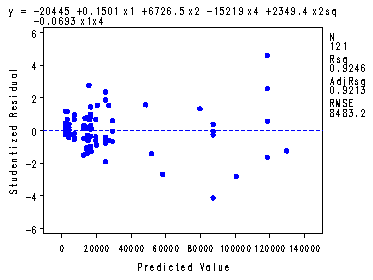
Looking at the best model consisting of x1, x2, x4, x2sq and x1x4, studentized residual plot, cook’s d, vif’s.
The Studentized Residual plot is Fig. 11.13b, p. 487.
symbol1 v=dot c=blue h=.8; proc reg data = center; model y = x1 x2 x4 x2sq x1x4/vif; plot student.*p.; output out = temp cookd = cookd r=r; run; quit; proc print data = temp; where cookd > .3; var cookd; run;
The REG Procedure Model: MODEL1 Dependent Variable: yAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 5 1.014399E11 20287971900 281.91 <.0001 Error 115 8275969776 71964955 Corrected Total 120 1.097158E11
Root MSE 8483.21605 R-Square 0.9246 Dependent Mean 19438 Adj R-Sq 0.9213 Coeff Var 43.64314
Parameter Estimates
Parameter Standard Variance Variable Label DF Estimate Error t Value Pr > |t| Inflation
Intercept Intercept 1 -20445 7409.59780 -2.76 0.0067 0 x1 ctypop 1 0.15006 0.00942 15.92 <.0001 16.07236 x2 lanes 1 6726.51683 946.81627 7.10 <.0001 2.52639 x4 control 1 -15219 2536.25608 -6.00 <.0001 1.87487 x2sq 1 2349.44748 367.04996 6.40 <.0001 1.63001 x1x4 1 -0.06926 0.00542 -12.79 <.0001 15.49519 Obs cookd
58 0.46168 64 0.47268 72 0.45639
Weighted LS Analysis: using a standard deviation function, p. 486-488, Fig. 11.14.
We have skipped this example.
Table 11.8 was not reproduced.