Applied Linear Statistical Models by Neter, Kutner, et. al. Chapter 16: Single-Factor ANOVA Model and Tests

Inputting the Kenton Food company data, table 16.1, p. 677.

data food;
  input sales design store;
cards;
  11  1  1
  17  1  2
  16  1  3
  14  1  4
  15  1  5
  12  2  1
  10  2  2
  15  2  3
  19  2  4
  11  2  5
  23  3  1
  20  3  2
  18  3  3
  17  3  4
  27  4  1
  33  4  2
  22  4  3
  26  4  4
  28  4  5
;
run;

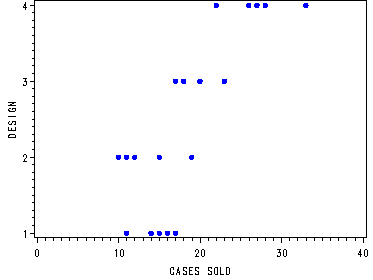
Fig. 16.3, p. 677.

goptions reset=all;
 
symbol1 v=dot c=blue h=.8;
axis1 order=(0 to 40 by 10) label=('CASES SOLD');
axis2 label=(angle=90 'DESIGN');
proc gplot data=food;
  plot design*sales/ haxis=axis1 vaxis=axis2;
run;
quit;

Calculations of SSTO, SSTR and SSE, p. 683 as well as the least squares and maximum likelihood estimates of the mean sales per store by package design, p. 679. Also included is the F-test, p. 691.

proc glm data=food;
  class design;
  model sales=design;
  means design;
  output out=temp r=resid;
run;
quit;

The GLM Procedure

Class Level Information

Class Levels Values design 4 1 2 3 4

Number of observations 19

The GLM Procedure

Dependent Variable: sales Sum of Source DF Squares Mean Square F Value Pr > F Model 3 588.2210526 196.0736842 18.59 <.0001 Error 15 158.2000000 10.5466667 Corrected Total 18 746.4210526 R-Square Coeff Var Root MSE sales Mean

0.788055 17.43042 3.247563 18.63158 Source DF Type I SS Mean Square F Value Pr > F design 3 588.2210526 196.0736842 18.59 <.0001 Source DF Type III SS Mean Square F Value Pr > F design 3 588.2210526 196.0736842 18.59 <.0001

The GLM Procedure

Level of ————sales———— design N Mean Std Dev 1 5 14.6000000 2.30217289 2 5 13.4000000 3.64691651 3 4 19.5000000 2.64575131 4 5 27.2000000 3.96232255

Table 16.2, p. 680.

proc freq data=temp;
  weight resid;
  tables design*store/ norow nocol nopercent table;
run;

The FREQ Procedure
Table of design by store
design     store
Frequency|       1|       2|       3|       4|       5|  Total
———+——–+——–+——–+——–+——–+
       1 |   -3.6 |    2.4 |    1.4 |   -0.6 |    0.4 | 18E-16
———+——–+——–+——–+——–+——–+
       2 |   -1.4 |   -3.4 |    1.6 |    5.6 |   -2.4 | 71E-16
———+——–+——–+——–+——–+——–+
       3 |    3.5 |    0.5 |   -1.5 |   -2.5 |      0 |      0
———+——–+——–+——–+——–+——–+
       4 |   -0.2 |    5.8 |   -5.2 |   -1.2 |    0.8 | 21E-15
———+——–+——–+——–+——–+——–+
Total        -1.7      5.3     -3.7      1.3     -1.2  302E-16

Coding Indicator variables to be used in the regression version of the Kenton Food example, p. 698.

data foodreg;
  set food;
  x1=0 ;
  if design=1 then x1=1;
  else if design=4 then x1=-1;
  x2=0 ;
  if design=2 then x2=1;
  else if design=4 then x2=-1;
  x3=0 ;
  if design=3 then x3=1;
  else if design=4 then x3=-1;
run;

Table 16.4a, p. 699.

proc print data=foodreg (obs=15);
run;

Obs sales design store x1 x2 x3

1 11 1 1 1 0 0 2 17 1 2 1 0 0 3 16 1 3 1 0 0 4 14 1 4 1 0 0 5 15 1 5 1 0 0 6 12 2 1 0 1 0 7 10 2 2 0 1 0 8 15 2 3 0 1 0 9 19 2 4 0 1 0 10 11 2 5 0 1 0 11 23 3 1 0 0 1 12 20 3 2 0 0 1 13 18 3 3 0 0 1 14 17 3 4 0 0 1 15 27 4 1 -1 -1 -1

Fitting the regression model, table 16.4b and 16.4c, p. 699.

proc reg data=foodreg;
  model sales = x1-x3;
run;
quit;

The REG Procedure Model: MODEL1 Dependent Variable: sales

Analysis of Variance

Sum of Mean Source DF Squares Square F Value Pr > F Model 3 588.22105 196.07368 18.59 <.0001 Error 15 158.20000 10.54667 Corrected Total 18 746.42105

Root MSE 3.24756 R-Square 0.7881 Dependent Mean 18.63158 Adj R-Sq 0.7457 Coeff Var 17.43042 Parameter Estimates

Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 18.67500 0.74853 24.95 <.0001 x1 1 -4.07500 1.27081 -3.21 0.0059 x2 1 -5.27500 1.27081 -4.15 0.0009 x3 1 0.82500 1.37063 0.60 0.5562