Inputting the Kenton Food company data, table 16.1, p. 677.
data food; input sales design store; cards; 11 1 1 17 1 2 16 1 3 14 1 4 15 1 5 12 2 1 10 2 2 15 2 3 19 2 4 11 2 5 23 3 1 20 3 2 18 3 3 17 3 4 27 4 1 33 4 2 22 4 3 26 4 4 28 4 5 ; run;
Fitting a one-way ANOVA model to the Kenton Food data, table 17.1, p. 711.
proc glm data=food; class design; model sales = design; lsmeans design; run; quit;
The GLM ProcedureClass Level Information
Class Levels Values design 4 1 2 3 4
Number of observations 19 The GLM Procedure Dependent Variable: sales Sum of Source DF Squares Mean Square F Value Pr > F Model 3 588.2210526 196.0736842 18.59 <.0001 Error 15 158.2000000 10.5466667 Corrected Total 18 746.4210526 R-Square Coeff Var Root MSE sales Mean 0.788055 17.43042 3.247563 18.63158 Source DF Type I SS Mean Square F Value Pr > F design 3 588.2210526 196.0736842 18.59 <.0001 Source DF Type III SS Mean Square F Value Pr > F design 3 588.2210526 196.0736842 18.59 <.0001
The GLM Procedure Least Squares Means
design sales LSMEAN 1 14.6000000 2 13.4000000 3 19.5000000 4 27.2000000
Inputting the Rust Inhibitor data, table 17.2a, p. 712.
data Rust; input performance brand experiment; cards; 43.9 1 1 39.0 1 2 46.7 1 3 43.8 1 4 44.2 1 5 47.7 1 6 43.6 1 7 38.9 1 8 43.6 1 9 40.0 1 10 89.8 2 1 87.1 2 2 92.7 2 3 90.6 2 4 87.7 2 5 92.4 2 6 86.1 2 7 88.1 2 8 90.8 2 9 89.1 2 10 68.4 3 1 69.3 3 2 68.5 3 3 66.4 3 4 70.0 3 5 68.1 3 6 70.6 3 7 65.2 3 8 63.8 3 9 69.2 3 10 36.2 4 1 45.2 4 2 40.7 4 3 40.5 4 4 39.3 4 5 40.3 4 6 43.2 4 7 38.7 4 8 40.9 4 9 39.7 4 10 ; run;
ANOVA of the Rust data and calculating the factor means and the grand mean, table 17.2b, p. 712.
ods output LSMeans=temp ; proc glm data=rust; class brand; model performance=brand; lsmeans brand; run; quit;
The GLM ProcedureClass Level Information
Class Levels Values brand 4 1 2 3 4
Number of observations 40 The GLM Procedure Dependent Variable: performance Sum of Source DF Squares Mean Square F Value Pr > F Model 3 15953.46600 5317.82200 866.12 <.0001 Error 36 221.03400 6.13983 Corrected Total 39 16174.50000 R-Square Coeff Var Root MSE performance Mean 0.986334 4.112645 2.477869 60.25000 Source DF Type I SS Mean Square F Value Pr > F brand 3 15953.46600 5317.82200 866.12 <.0001 Source DF Type III SS Mean Square F Value Pr > F brand 3 15953.46600 5317.82200 866.12 <.0001
The GLM Procedure Least Squares Means
performance brand LSMEAN 1 43.1400000 2 89.4400000 3 67.9500000 4 40.4700000
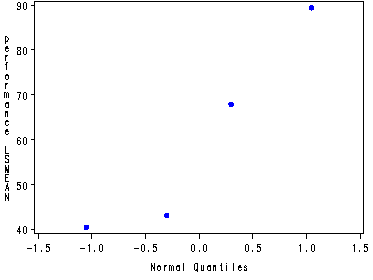
Plotting the normal probability plot using the data set temp created in the proc glm, fig. 17.3b, p. 715.
Note: The format options was to get rid of all the extra decimal places in the performance lsmeans as seen in the above output.
goptions reset=all; symbol v=dot c=blue h=.8; proc capability data=temp noprint ; format performanceLSMean 10.2; qqplot performanceLSMean; run;
Obtaining the 95% confidence interval for the estimated mean sales by level of design, p. 718.
proc glm data=food; class design; model sales=design; lsmeans design / cl; run; quit;
The GLM Procedure <output omitted>Least Squares Means
design sales LSMEAN 1 14.6000000 2 13.4000000 3 19.5000000 4 27.2000000
design sales LSMEAN 95% Confidence Limits 1 14.600000 11.504380 17.695620 2 13.400000 10.304380 16.495620 3 19.500000 16.038991 22.961009 4 27.200000 24.104380 30.295620
Testing the difference in mean sales for design levels 3 and 4, p 719.
proc glm data = food; class design; model sales = design / clparm; estimate 'd3 v d4' design 0 0 1 -1; run; quit;
The GLM Procedure<output omitted> Standard Parameter Estimate Error t Value Pr > |t| 95% Confidence Limits d3 v d4 -7.70000000 2.17853162 -3.53 0.0030 -12.34343022 -3.05656978
Testing several contrasts all at once, p. 720-721.
Note: The contrast (d1, d2) vs. (d3, d4) is shown in detail on p. 722-723.
proc glm data = food; class design; model sales = design / clparm; estimate 'design=1 vs. design=2' design 1 -1 0 0; estimate '(d1, d2) vs. (d3, d4)' design .5 .5 -.5 -.5; estimate '(d1, d3) vs. (d2, d4)' design .5 -.5 .5 -.5; estimate 'd1 vs. (d2, d3, d4)' design .75 -.25 -.25 -.25; run; quit;
The GLM Procedure<output omitted> Standard Parameter Estimate Error t Value Pr > |t| 95% Confidence Limits design=1 vs. design=2 1.20000000 2.05393930 0.58 0.5677 -3.17786800 5.57786800 (d1, d2) vs. (d3, d4) -9.35000000 1.49705266 -6.25 <.0001 -12.54089221 -6.15910779 (d1, d3) vs. (d2, d4) -3.25000000 1.49705266 -2.17 0.0464 -6.44089221 -0.05910779 d1 vs. (d2, d3, d4) -4.07500000 1.27081011 -3.21 0.0059 -6.78366763 -1.36633237
Inferences for linear combination of factor level means, p. 723.
Note: The coefficients in the estimate statement add to zero, the last coefficient is -.75 instead of .25.
proc glm data=food; class design; model sales = design; estimate 'lin comb' design .35 .28 .12 -0.75; run; quit;
The GLM Procedure<output omitted> Standard Parameter Estimate Error t Value Pr > |t| lin comb -9.19800000 1.28383530 -7.16 <.0001
Tukey Multiple comparisons procedure for the Rust data, p. 728-729.
Note: In proc glm the pair-wise comparisons including confidence intervals can be obtained using either the means statement with the cl and tukey options or with the lsmeans statement with the cl, adjust=tukey pdiff options.
proc glm data=rust; class brand; model performance=brand; lsmeans brand/ cl adjust=tukey pdiff; means brand/ tukey alpha=.05 cldiff; ods output lsmeans=temp; run; quit;
The GLM ProcedureClass Level Information
Class Levels Values brand 4 1 2 3 4
Number of observations 40 The GLM Procedure Dependent Variable: performance Sum of Source DF Squares Mean Square F Value Pr > F Model 3 15953.46600 5317.82200 866.12 <.0001 Error 36 221.03400 6.13983 Corrected Total 39 16174.50000 R-Square Coeff Var Root MSE performance Mean 0.986334 4.112645 2.477869 60.25000 Source DF Type I SS Mean Square F Value Pr > F brand 3 15953.46600 5317.82200 866.12 <.0001 Source DF Type III SS Mean Square F Value Pr > F brand 3 15953.46600 5317.82200 866.12 <.0001
The GLM Procedure Least Squares Means Adjustment for Multiple Comparisons: Tukey
performance LSMEAN brand LSMEAN Number 1 43.1400000 1 2 89.4400000 2 3 67.9500000 3 4 40.4700000 4 Least Squares Means for effect brand Pr > |t| for H0: LSMean(i)=LSMean(j)
Dependent Variable: performance
i/j 1 2 3 4 1 <.0001 <.0001 0.0933 2 <.0001 <.0001 <.0001 3 <.0001 <.0001 <.0001 4 0.0933 <.0001 <.0001 performance brand LSMEAN 95% Confidence Limits 1 43.140000 41.550845 44.729155 2 89.440000 87.850845 91.029155 3 67.950000 66.360845 69.539155 4 40.470000 38.880845 42.059155 Least Squares Means for Effect brand
Difference Simultaneous 95% Between Confidence Limits for i j Means LSMean(i)-LSMean(j) 1 2 -46.300000 -49.284464 -43.315536 1 3 -24.810000 -27.794464 -21.825536 1 4 2.670000 -0.314464 5.654464 2 3 21.490000 18.505536 24.474464 2 4 48.970000 45.985536 51.954464 3 4 27.480000 24.495536 30.464464
The GLM Procedure
Tukey’s Studentized Range (HSD) Test for performance NOTE: This test controls the Type I experimentwise error rate
Alpha 0.05 Error Degrees of Freedom 36 Error Mean Square 6.139833 Critical Value of Studentized Range 3.80880 Minimum Significant Difference 2.9845 Comparisons significant at the 0.05 level are indicated by ***.
Difference brand Between Simultaneous 95% Comparison Means Confidence Limits 2 – 3 21.490 18.506 24.474 *** 2 – 1 46.300 43.316 49.284 *** 2 – 4 48.970 45.986 51.954 *** 3 – 2 -21.490 -24.474 -18.506 *** 3 – 1 24.810 21.826 27.794 *** 3 – 4 27.480 24.496 30.464 *** 1 – 2 -46.300 -49.284 -43.316 *** 1 – 3 -24.810 -27.794 -21.826 *** 1 – 4 2.670 -0.314 5.654 4 – 2 -48.970 -51.954 -45.986 *** 4 – 3 -27.480 -30.464 -24.496 *** 4 – 1 -2.670 -5.654 0.314
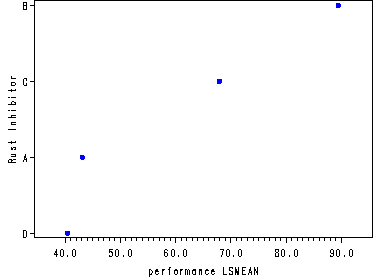
Fig. 17.4, paired comparison plot, p. 728.
data temp;
set temp;
b = brand +0;
run;
goptions reset=all;
symbol v=dot c=blue h=.8;
axis1 order=(40 to 90 by 10) offset=(5, 5);
axis2 order=(4 1 3 2) value=('D' 'A' 'C' 'B') label=(a=90 'Rust Inhibitor');
proc gplot data=temp;
format lsmean 12.1;
plot b*LSMean / haxis=axis1 vaxis=axis2;
run;
quit;
Tukey Multiple comparisons for the Kenton Food data, p. 730-731.
proc glm data=food; class design; model sales=design; means design/ tukey alpha=.1 cldiff; run; quit;
The GLM Procedure<output omitted>
Tukey’s Studentized Range (HSD) Test for sales NOTE: This test controls the Type I experimentwise error rate
Alpha 0.1 Error Degrees of Freedom 15 Error Mean Square 10.54667 Critical Value of Studentized Range 3.53989 Comparisons significant at the 0.1 level are indicated by ***.
Difference design Between Simultaneous 90% Comparison Means Confidence Limits 4 – 3 7.700 2.247 13.153 *** 4 – 1 12.600 7.459 17.741 *** 4 – 2 13.800 8.659 18.941 *** 3 – 4 -7.700 -13.153 -2.247 *** 3 – 1 4.900 -0.553 10.353 3 – 2 6.100 0.647 11.553 *** 1 – 4 -12.600 -17.741 -7.459 *** 1 – 3 -4.900 -10.353 0.553 1 – 2 1.200 -3.941 6.341 2 – 4 -13.800 -18.941 -8.659 *** 2 – 3 -6.100 -11.553 -0.647 *** 2 – 1 -1.200 -6.341 3.941
The Scheffe comparisons procedure for the Kenton Food data, p. 734-735.
Note1: Any pair-wise comparison and confidence interval can be obtained from the means statement by using the scheffe option. However, for non pair-wise comparisons the confidence interval has to be computed separately.
Note2: The comparison of L1 and L2 and their confidence intervals have been italicized in the output from the means statement.
ods output Estimates=est overallanova=anova;
proc glm data=food;
class design;
model sales=design;
means design/ scheffe alpha=.1;
estimate 'd1,d2 v. d3,d4' design .5 .5 -.5 -.5;
estimate 'd1,d3 v. d2,d4' design .5 -.5 .5 -.5;
run;
quit;
data _null_;
set anova;
if source='Model' then call symput('dfm', df);
if source='Error' then call symput('dfe', df);
run;
%put here are the numbers &dfm &dfe;
data est1;
set est;
drop dependent tvalue probt;
S2=&dfm*finv(.90, &dfm, &dfe);
S=sqrt(S2);
lower=estimate - stderr*S;
upper=estimate + stderr*S;
run;
proc print data=est1;
run;
The GLM Procedure<output omitted>
Scheffe’s Test for sales NOTE: This test controls the Type I experimentwise error rate, but it generally has a higher Type II error rate than Tukey’s for all pairwise comparisons
Alpha 0.1 Error Degrees of Freedom 15 Error Mean Square 10.54667 Critical Value of F 2.48979 Comparisons significant at the 0.1 level are indicated by ***.
Difference design Between Simultaneous 90% Comparison Means Confidence Limits 4 – 3 7.700 1.746 13.654 *** 4 – 1 12.600 6.987 18.213 *** 4 – 2 13.800 8.187 19.413 *** 3 – 4 -7.700 -13.654 -1.746 *** 3 – 1 4.900 -1.054 10.854 3 – 2 6.100 0.146 12.054 *** 1 – 4 -12.600 -18.213 -6.987 *** 1 – 3 -4.900 -10.854 1.054 1 – 2 1.200 -4.413 6.813 2 – 4 -13.800 -19.413 -8.187 *** 2 – 3 -6.100 -12.054 -0.146 *** 2 – 1 -1.200 -6.813 4.413
The GLM Procedure
Dependent Variable: sales Standard Parameter Estimate Error t Value Pr > |t| d1,d2 v. d3,d4 -9.35000000 1.49705266 -6.25 <.0001 d1,d3 v. d2,d4 -3.25000000 1.49705266 -2.17 0.0464 Obs Parameter Estimate StdErr S2 S lower upper
1 d1,d2 v. d3,d4 -9.35000000 1.49705266 7.46936 2.73301 -13.4415 -5.25853 2 d1,d3 v. d2,d4 -3.25000000 1.49705266 7.46936 2.73301 -7.3415 0.84147
Bonferroni comparisons procedure for the Kenton food data, p. 736-737. Using the datasets and the macro variables created for the Scheffe comparisons procedure above since we are considering the exact same comparisons. This time we are looking for a 97.5% confidence interval.
%put this is the macro variable we are using again &dfe; data est2; set est; drop dependent tvalue probt; B=tinv( (1 - .025/(2*2)), &dfe); lower=estimate - stderr*B; upper=estimate + stderr*B; run; proc print data=est2; run;
Obs Parameter Estimate StdErr B lower upper1 d1,d2 v. d3,d4 -9.35000000 1.49705266 2.83663 -13.5966 -5.10342 2 d1,d3 v. d2,d4 -3.25000000 1.49705266 2.83663 -7.4966 0.99658
Holm testing procedure for six specific comparisons, table 17.5, p. 741.
Note: First we create the data set with the p-values and then we use proc multtest.
ods output estimates=estimate; ods listing close; proc glm data=food; class design; model sales=design; estimate 'L1' design .5 .5 -.5 -.5; estimate 'L2' design .5 -.5 .5 -.5; estimate 'L3' design 1 -1 0 0; estimate 'L4' design 1 0 -1 0; estimate 'L5' design 0 1 0 -1; estimate 'L6' design 0 0 1 -1; run; quit; ods output close; ods listing; data estimate; set estimate; format probt 10.8; drop dependent; run; proc rank data=estimate out=order ties=low; var probt; ranks probtrank; run; proc print data=order; run; data pvalue; set estimate; keep parameter probt; rename probt = raw_p; run; proc multtest pdata=pvalue holm pvals out=new; run; data new; set new; Conclusion='H0'; if stpbon_p < .05 then Conclusion='Ha'; rename raw_p = probt; run; proc rank data=new out=holm ties=low; var probt; ranks prank; run; proc sort data=holm; by prank; run; proc print data=holm; var prank parameter probt stpbon_p Conclusion; run;
Obs Parameter Estimate StdErr tValue Probt probtrank1 L1 -9.3500000 1.49705266 -6.25 0.00001568 2 2 L2 -3.2500000 1.49705266 -2.17 0.04639440 5 3 L3 1.2000000 2.05393930 0.58 0.56774020 6 4 L4 -4.9000000 2.17853162 -2.25 0.03994770 4 5 L5 -13.8000000 2.05393930 -6.72 0.00000688 1 6 L6 -7.7000000 2.17853162 -3.53 0.00300329 3
The Multtest Procedure
p-Values
Stepdown Test Raw Bonferroni 1 <.0001 <.0001 2 0.0464 0.1198 3 0.5677 0.5677 4 0.0399 0.1198 5 <.0001 <.0001 6 0.0030 0.0120 Obs prank Parameter probt stpbon_p Conclusion
1 1 L5 0.00000688 0.00004 Ha 2 2 L1 0.00001568 0.00008 Ha 3 3 L6 0.00300329 0.01201 Ha 4 4 L4 0.03994770 0.11984 H0 5 5 L2 0.04639440 0.11984 H0 6 6 L3 0.56774020 0.56774 H0
Calculating the Bonferroni confidence intervals, p. 741, using the estimate dataset from proc glm and the macro variable for Error degrees of freedom ( 15) obtained previously.
data est5; set estimate; B=tinv( (1 - .025/(2*2)), &dfe); lower=estimate - stderr*B; upper=estimate + stderr*B; run; proc print data=est5; var parameter tvalue stderr B lower upper; run;
Obs Parameter tValue StdErr B lower upper1 L1 -6.25 1.49705266 2.83663 -13.5966 -5.10342 2 L2 -2.17 1.49705266 2.83663 -7.4966 0.99658 3 L3 0.58 2.05393930 2.83663 -4.6263 7.02626 4 L4 -2.25 2.17853162 2.83663 -11.0797 1.27968 5 L5 -6.72 2.05393930 2.83663 -19.6263 -7.97374 6 L6 -3.53 2.17853162 2.83663 -13.8797 -1.52032
Inputting the Piecework Trainee data, table 17.6, p. 743.
data trainee; input units treat employee; cards; 40 1 1 39 1 2 39 1 3 36 1 4 42 1 5 43 1 6 41 1 7 53 2 1 48 2 2 49 2 3 50 2 4 51 2 5 50 2 6 48 2 7 53 3 1 58 3 2 56 3 3 59 3 4 53 3 5 59 3 6 58 3 7 63 4 1 62 4 2 59 4 3 61 4 4 62 4 5 62 4 6 61 4 7 ; run;
Fig. 17.5, p. 744.
Note: Instead of the homogenous subsets table proc glm outputs a table of p-values for pair-wise tests of all groups using a Tukey procedure as a result of the pdiff and adjust=tukey options in the lsmeans statement.
proc glm data=trainee; class treat; model units=treat; lsmeans treat/ pdiff adjust=tukey ; run; quit;
The GLM ProcedureClass Level Information
Class Levels Values treat 4 1 2 3 4
Number of observations 28 The GLM Procedure Dependent Variable: units Sum of Source DF Squares Mean Square F Value Pr > F
Model 3 1808.678571 602.892857 141.46 <.0001 Error 24 102.285714 4.261905 Corrected Total 27 1910.964286 R-Square Coeff Var Root MSE units Mean 0.946474 3.972802 2.064438 51.96429 Source DF Type I SS Mean Square F Value Pr > F
treat 3 1808.678571 602.892857 141.46 <.0001 Source DF Type III SS Mean Square F Value Pr > F
treat 3 1808.678571 602.892857 141.46 <.0001 The GLM Procedure Least Squares Means Adjustment for Multiple Comparisons: Tukey LSMEAN treat units LSMEAN Number 1 40.0000000 1 2 49.8571429 2 3 56.5714286 3 4 61.4285714 4 Least Squares Means for effect treat Pr > |t| for H0: LSMean(i)=LSMean(j)
Dependent Variable: units
i/j 1 2 3 4 1 <.0001 <.0001 <.0001 2 <.0001 <.0001 <.0001 3 <.0001 <.0001 0.0010 4 <.0001 <.0001 0.0010
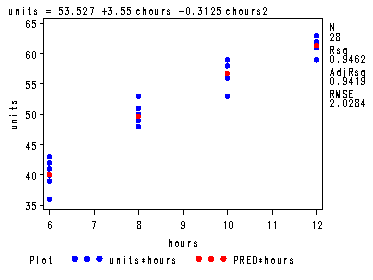
Table 17.8a and fig. 17.6, p. 745-746.
data temp; set trainee; hours=0; if treat=1 then hours=6; else if treat=2 then hours=8; else if treat=3 then hours=10; else hours=12; run; proc sql; create table center as select *, hours - mean(hours) as chours, (hours - mean(hours))*(hours - mean(hours)) as chours2 from temp; quit; goptions reset=all; filename outfile 'c:sas2htmhttps://stats.idre.ucla.edu/wp-content/uploads/2016/02/alsm17_3.gif'; goptions gsfname=outfile dev=gif373; symbol1 v=dot c=blue h=.8; symbol2 v=dot c=red h=.8 i=join; proc reg data=center; var hours; model units = chours chours2; plot (units p.)*hours / overlay; ods output anova=reg; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: unitsAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F Model 2 1808.10000 904.05000 219.72 <.0001 Error 25 102.86429 4.11457 Corrected Total 27 1910.96429
Root MSE 2.02844 R-Square 0.9462 Dependent Mean 51.96429 Adj R-Sq 0.9419 Coeff Var 3.90353 Parameter Estimates
Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 53.52679 0.61364 87.23 <.0001 chours 1 3.55000 0.17143 20.71 <.0001 chours2 1 -0.31250 0.09583 -3.26 0.0032
Table 17.8b, p. 746.
proc glm data=center; class treat; model units=treat; ods output overallanova=glm; run; quit;
The GLM ProcedureClass Level Information
Class Levels Values treat 4 1 2 3 4
Number of observations 28 The GLM Procedure Dependent Variable: units Sum of Source DF Squares Mean Square F Value Pr > F Model 3 1808.678571 602.892857 141.46 <.0001 Error 24 102.285714 4.261905 Corrected Total 27 1910.964286 R-Square Coeff Var Root MSE units Mean 0.946474 3.972802 2.064438 51.96429 Source DF Type I SS Mean Square F Value Pr > F treat 3 1808.678571 602.892857 141.46 <.0001 Source DF Type III SS Mean Square F Value Pr > F treat 3 1808.678571 602.892857 141.46 <.0001
Table 17.8c, lack of fit test, p. 746, using the datasets reg from the proc reg and glm from the proc glm.
data _null_;
set reg;
if source='Model' then call symput('df', df);
if source='Error' then call symput('ssreg', ss);
run;
data _null_;
set glm;
if source='Error' then call symput('ssglm', ss);
if source='Error' then call symput('dfglm', df);
run;
%put df=&df and ssreg=&ssreg and ssglm=&ssglm and dfsspe = &dfglm; /*to check in the log file*/
data temp;
sslf = &ssreg - &ssglm;
df = 4 - (&df + 1);
sspe=&ssglm;
dfsspe = &dfglm;
f = (sslf/df) / ( &ssglm/&dfglm);
critvalue = finv(.95, df, &dfglm);
pvalue = 1- probf( f, df, &dfglm);
run;
proc print data=temp;
run;
Obs sslf df sspe dfsspe f critvalue pvalue1 0.57857 1 102.286 24 0.13575 4.25968 0.71577