Inputting the Rust Inhibitor data, table 17.2a, p. 712.
data Rust; input performance brand experiment; cards; 43.9 1 1 39.0 1 2 46.7 1 3 43.8 1 4 44.2 1 5 47.7 1 6 43.6 1 7 38.9 1 8 43.6 1 9 40.0 1 10 89.8 2 1 87.1 2 2 92.7 2 3 90.6 2 4 87.7 2 5 92.4 2 6 86.1 2 7 88.1 2 8 90.8 2 9 89.1 2 10 68.4 3 1 69.3 3 2 68.5 3 3 66.4 3 4 70.0 3 5 68.1 3 6 70.6 3 7 65.2 3 8 63.8 3 9 69.2 3 10 36.2 4 1 45.2 4 2 40.7 4 3 40.5 4 4 39.3 4 5 40.3 4 6 43.2 4 7 38.7 4 8 40.9 4 9 39.7 4 10 ; run;
Table 18.1, p. 758.
proc glm data=rust noprint; class brand; model performance = brand; output out=temp r=resid p=predict; run; proc freq data=temp; weight resid; table experiment*brand/ norow nocol nopercent ; run;
The FREQ ProcedureTable of experiment by brand experiment brand
Frequency| 1| 2| 3| 4| Total ———+——–+——–+——–+——–+ 1 | 0.76 | 0.36 | 0.45 | -4.27 | -2.7 ———+——–+——–+——–+——–+ 2 | -4.14 | -2.34 | 1.35 | 4.73 | -0.4 ———+——–+——–+——–+——–+ 3 | 3.56 | 3.26 | 0.55 | 0.23 | 7.6 ———+——–+——–+——–+——–+ 4 | 0.66 | 1.16 | -1.55 | 0.03 | 0.3 ———+——–+——–+——–+——–+ 5 | 1.06 | -1.74 | 2.05 | -1.17 | 0.2 ———+——–+——–+——–+——–+ 6 | 4.56 | 2.96 | 0.15 | -0.17 | 7.5 ———+——–+——–+——–+——–+ 7 | 0.46 | -3.34 | 2.65 | 2.73 | 2.5 ———+——–+——–+——–+——–+ 8 | -4.24 | -1.34 | -2.75 | -1.77 | -10.1 ———+——–+——–+——–+——–+ 9 | 0.46 | 1.36 | -4.15 | 0.43 | -1.9 ———+——–+——–+——–+——–+ 10 | -3.14 | -0.34 | 1.25 | -0.77 | -3 ———+——–+——–+——–+——–+ Total 0 0 -28E-15 377E-15 348E-15
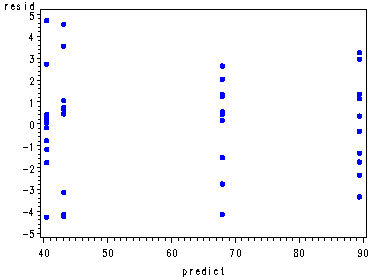
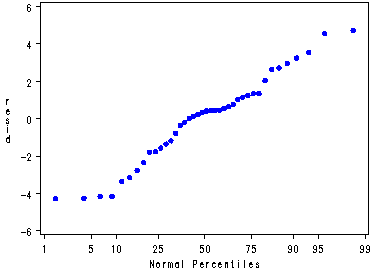
Univariate analysis of the residual, fig. 18.1, p. 759.
goptions reset=all; symbol v=dot c=blue h=.8; proc gplot data=temp; plot resid*predict; run; quit; proc univariate data=temp noprint; var resid; probplot resid; run;
Inputting ABT Electronics data, table 18.2, p. 765.
data Electronics; input strength type joint; cards; 14.87 1 1 16.81 1 2 15.83 1 3 15.47 1 4 13.60 1 5 14.76 1 6 17.40 1 7 14.62 1 8 18.43 2 1 18.76 2 2 20.12 2 3 19.11 2 4 19.81 2 5 18.43 2 6 17.16 2 7 16.40 2 8 16.95 3 1 12.28 3 2 12.00 3 3 13.18 3 4 14.99 3 5 15.76 3 6 19.35 3 7 15.52 3 8 8.59 4 1 10.90 4 2 8.60 4 3 10.13 4 4 10.28 4 5 9.98 4 6 9.41 4 7 10.04 4 8 11.55 5 1 13.36 5 2 13.64 5 3 12.16 5 4 11.62 5 5 12.39 5 6 12.05 5 7 11.95 5 8 ; run;
Table 18.2, the mean, median and variance of pull strength by flux type, p. 765.
proc means data=electronics mean median var; class type; var strength; run;
The MEANS ProcedureAnalysis Variable : strength
N type Obs Mean Median Variance ——————————————————————- 1 8 15.4200000 15.1700000 1.5305143 2 8 18.5275000 18.5950000 1.5699357 3 8 15.0037500 15.2550000 6.1833982 4 8 9.7412500 10.0100000 0.6668411 5 8 12.3400000 12.1050000 0.5920000 ——————————————————————-
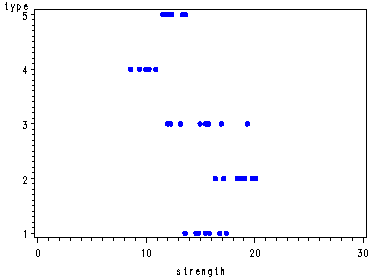
Fig. 18.6, p. 766.
goptions reset=all; symbol v=dot c=blue h=.8; axis1 order=(0 to 30 by 10); proc gplot data=electronics; plot type*strength / haxis=axis1; run; quit;
The Hartley test for equal variances.
Note: SAS does not have the an inverse Hartley distribution function, so the critical value has to be obtained from another source.
ods listing close;
proc means data=electronics var;
class type;
var strength;
ods output summary=temp;
run;
ods listing;
ods output close;
proc sql;
select max(Strength_Var) as max, min(Strength_Var) as min, 9.70 as critvalue,
max(Strength_Var)/min(Strength_Var) as H
from temp;
quit;
max min critvalue H ————————————— 6.183398 0.592 9.7000 10.44493
Modified Levene Test, p. 767.
proc reg data=electronics noprint; model strength = type; output out=temp r=r; run; proc means data = temp noprint; by type; var r; output out=mout median=mr; run; proc print data = mout; var type mr; run; data mtemp; merge temp mout; by type; d = abs(r - mr); run; proc anova data=mtemp; class type; model d = type; run; quit;
Obs type mr1 1 -2.02575 2 2 2.89387 3 3 1.04850 4 4 -2.70187 5 5 0.88775
The ANOVA Procedure
Class Level Information
Class Levels Values type 5 1 2 3 4 5
Number of observations 40
The ANOVA Procedure
Dependent Variable: d
Sum of Source DF Squares Mean Square F Value Pr > F Model 4 9.34771500 2.33692875 2.94 0.0341 Error 35 27.86062500 0.79601786 Corrected Total 39 37.20834000 R-Square Coeff Var Root MSE d Mean
0.251226 90.76280 0.892198 0.983000 Source DF Anova SS Mean Square F Value Pr > F
type 4 9.34771500 2.33692875 2.94 0.0341
Table 18.3, p. 768.
proc freq data= mtemp; weight d; tables joint*type / nocol norow nopercent; run;
The FREQ ProcedureTable of joint by type joint type
Frequency| 1| 2| 3| 4| 5| Total ———+——–+——–+——–+——–+——–+ 1 | 0.3 | 0.165 | 1.695 | 1.42 | 0.555 | 4.135 ———+——–+——–+——–+——–+——–+ 2 | 1.64 | 0.165 | 2.975 | 0.89 | 1.255 | 6.925 ———+——–+——–+——–+——–+——–+ 3 | 0.66 | 1.525 | 3.255 | 1.41 | 1.535 | 8.385 ———+——–+——–+——–+——–+——–+ 4 | 0.3 | 0.515 | 2.075 | 0.12 | 0.055 | 3.065 ———+——–+——–+——–+——–+——–+ 5 | 1.57 | 1.215 | 0.265 | 0.27 | 0.485 | 3.805 ———+——–+——–+——–+——–+——–+ 6 | 0.41 | 0.165 | 0.505 | 0.03 | 0.285 | 1.395 ———+——–+——–+——–+——–+——–+ 7 | 2.23 | 1.435 | 4.095 | 0.6 | 0.055 | 8.415 ———+——–+——–+——–+——–+——–+ 8 | 0.55 | 2.195 | 0.265 | 0.03 | 0.155 | 3.195 ———+——–+——–+——–+——–+——–+ Total 7.66 7.38 15.13 4.77 4.38 39.32
Creating the weights and the dummy variables for type to be used in the weighted least squares regression. Table 18.4, p. 769-771.
data temp; set electronics; x1 = 0; if type=1 then x1 = 1; x2 = 0; if type=2 then x2 = 1; x3 = 0; if type=3 then x3 = 1; x4 = 0; if type=4 then x4 = 1; x5=0; if type=5 then x5 = 1; x=1; run; proc sql; create table temp1 as select *, 1/( var( strength) ) as w from temp group by type; quit; proc print data=temp1 (obs=20); run;
Obs strength type joint x1 x2 x3 x4 x5 x w1 14.87 1 1 1 0 0 0 0 1 0.65338 2 16.81 1 2 1 0 0 0 0 1 0.65338 3 17.40 1 7 1 0 0 0 0 1 0.65338 4 15.47 1 4 1 0 0 0 0 1 0.65338 5 13.60 1 5 1 0 0 0 0 1 0.65338 6 15.83 1 3 1 0 0 0 0 1 0.65338 7 14.76 1 6 1 0 0 0 0 1 0.65338 8 14.62 1 8 1 0 0 0 0 1 0.65338 9 18.43 2 6 0 1 0 0 0 1 0.63697 10 19.81 2 5 0 1 0 0 0 1 0.63697 11 17.16 2 7 0 1 0 0 0 1 0.63697 12 19.11 2 4 0 1 0 0 0 1 0.63697 13 20.12 2 3 0 1 0 0 0 1 0.63697 14 18.76 2 2 0 1 0 0 0 1 0.63697 15 18.43 2 1 0 1 0 0 0 1 0.63697 16 16.40 2 8 0 1 0 0 0 1 0.63697 17 15.52 3 8 0 0 1 0 0 1 0.16172 18 15.76 3 6 0 0 1 0 0 1 0.16172 19 19.35 3 7 0 0 1 0 0 1 0.16172 20 14.99 3 5 0 0 1 0 0 1 0.16172
Fig. 18.7, p.771.
proc reg data=temp1; weight w; model strength = x1-x5 /noint; model strength = x / noint; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: strengthNOTE: No intercept in model. R-Square is redefined. Weight: w Analysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F Model 5 6479.49838 1295.89968 1295.90 <.0001 Error 35 35.00000 1.00000 Uncorrected Total 40 6514.49838
Root MSE 1.00000 R-Square 0.9946 Dependent Mean 12.87596 Adj R-Sq 0.9939 Coeff Var 7.76641
Parameter Estimates
Parameter Standard Variable DF Estimate Error t Value Pr > |t| x1 1 15.42000 0.43739 35.25 <.0001 x2 1 18.52750 0.44299 41.82 <.0001 x3 1 15.00375 0.87916 17.07 <.0001 x4 1 9.74125 0.28871 33.74 <.0001 x5 1 12.34000 0.27203 45.36 <.0001
The REG Procedure Model: MODEL2 Dependent Variable: strength NOTE: No intercept in model. R-Square is redefined. Weight: w Analysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F Model 1 6155.28528 6155.28528 668.28 <.0001 Error 39 359.21310 9.21059 Uncorrected Total 40 6514.49838
Root MSE 3.03490 R-Square 0.9449 Dependent Mean 12.87596 Adj R-Sq 0.9434 Coeff Var 23.57025 Parameter Estimates
Parameter Standard Variable DF Estimate Error t Value Pr > |t| x 1 12.87596 0.49808 25.85 <.0001
Inputting the Servo data and obtaining the mean and variance of time by location, table 18.5, p. 774.
data servo;
input time location interval ;
cards;
4.41 1 1
100.65 1 2
14.45 1 3
47.13 1 4
85.21 1 5
8.24 2 1
81.16 2 2
7.35 2 3
12.29 2 4
1.61 2 5
106.19 3 1
33.83 3 2
78.88 3 3
342.81 3 4
44.33 3 5
;
run;
proc means data=servo mean var;
class location;
var time;
run;
proc means data=servo mean;
var time;
run;
The MEANS ProcedureAnalysis Variable : time
N location Obs Mean Variance ————————————————— 1 5 50.3700000 1788.74 2 5 22.1300000 1103.45 3 5 121.2080000 16167.45 ————————————————— The MEANS Procedure
Analysis Variable : time
Mean ———— 64.5693333 ————
Diagnostic statistics for determining the appropriate transformation of time, bottom of p. 773.
proc sql;
select var(time)/mean(time) as sqroot, std(time)/mean(time) as log,
std(time)/( mean(time)*mean(time) ) as inv
from servo
group by location;
quit;
sqroot log inv —————————- 35.51206 0.839657 0.01667 49.86237 1.501052 0.067829 133.386 1.049034 0.008655
Boxcox transformation. There is a macro written by Michael Friendly at York University which will produce a table of lambda and the square root of MSE as well as a number of other graphs and tables. For more information please refer to http://www.math.yorku.ca/SCS/sasmac/boxcox.html .
%boxcox(data=servo, resp=time, model =location) ;
In SAS 9, we can also use proc transreg to produce Table 18.6.
options nocenter; proc transreg data = servo ss2 details; model boxcox(time /LAMBDA= -1 to 1 by .1)=identity(location); run;
Transformation Information
for BoxCox(time)
Lambda R-Square Log Like
-1.0 0.02 -74.3335
-0.9 0.02 -71.5357
-0.8 0.03 -68.8983
-0.7 0.03 -66.4439
-0.6 0.04 -64.1962
-0.5 0.05 -62.1784
-0.4 0.06 -60.4127
-0.3 0.06 -58.9185
-0.2 0.07 -57.7117 *
-0.1 0.08 -56.8044 *
0.0 + 0.09 -56.2050 *
0.1 0.10 -55.9184 <
0.2 0.10 -55.9460 *
0.3 0.11 -56.2859 *
0.4 0.11 -56.9316 *
0.5 0.12 -57.8723
0.6 0.12 -59.0916
0.7 0.12 -60.5688
0.8 0.12 -62.2798
0.9 0.12 -64.1984
1.0 0.12 -66.2985
< - Best Lambda * - Confidence Interval + - Convenient Lambda
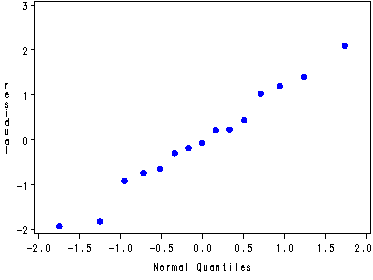
Variance of time by location, bottom of p. 774 and fig. 18.8a and 18.8b, p. 775.
data log; set servo; logtime = log(time); run; proc means data=log var; class location; var logtime; run; quit; proc glm data=servo noprint; class location; model time=location; output out=temp r=residual; run; quit; goptions reset=all; symbol1 v=dot c=blue; proc capability data=temp noprint; qqplot residual; run; proc glm data=log noprint; class location; model logtime=location; output out=temp r=residual; run; quit; symbol1 v=dot c=blue; proc capability data=temp noprint; qqplot residual; run;
The MEANS ProcedureAnalysis Variable : logtime
N location Obs Variance ———————————– 1 5 1.7420229 2 5 1.9735863 3 5 0.8180583 ———————————–
Nonparametric F-test and the Kruskal Wallis test of the Servo data, p. 778-779.
proc npar1way data=servo wilcoxon anova ;
class location;
var time;
ods output KruskalWallisTest=temp anova=temp1;
run;
data _null_;
set temp;
if label1='Chi-Square' then call symput('chisq', cvalue1);
run;
data _null_;
set temp1;
if source='Among' then call symput('between', df);
if source='Within' then call symput('within', df);
run;
data new;
fstat = ( &within*&chisq ) / ( &between*(&within+&between - &chisq) );
fcrit = finv(.9, &between, &within);
p_value = 1- cdf('F', fstat, &between, &within );
run;
proc print data=new;
run;
The NPAR1WAY ProcedureAnalysis of Variance for Variable time Classified by Variable location
location N Mean ————————————– 1 5 50.3700 2 5 22.1300 3 5 121.2080 Source DF Sum of Squares Mean Square F Value Pr > F ——————————————————————- Among 2 26053.283213 13026.64161 2.0504 0.1714 Within 12 76238.575080 6353.21459
The NPAR1WAY Procedure
Wilcoxon Scores (Rank Sums) for Variable time Classified by Variable location
Sum of Expected Std Dev Mean location N Scores Under H0 Under H0 Score ———————————————————————— 1 5 42.0 40.0 8.164966 8.40 2 5 24.0 40.0 8.164966 4.80 3 5 54.0 40.0 8.164966 10.80 Kruskal-Wallis Test Chi-Square 4.5600 DF 2 Pr > Chi-Square 0.1023 Obs fstat fcrit p_value
1 2.89831 2.80680 0.093986