Inputting the Growth Hormone data and computing the factor level means, table 22.1, p. 892.
data growth; input growth gender depress rep; cards; 1.4 1 1 1 2.4 1 1 2 2.2 1 1 3 2.1 1 2 1 1.7 1 2 2 0.7 1 3 1 1.1 1 3 2 2.4 2 1 1 2.5 2 2 1 1.8 2 2 2 2.0 2 2 3 0.5 2 3 1 0.9 2 3 2 1.3 2 3 3 ; run; proc means data=growth mean; class gender depress ; var growth; run;
The MEANS ProcedureAnalysis Variable : growth
N gender depress Obs Mean ————————————————— 1 1 3 2.0000000 2 2 1.9000000 3 2 0.9000000 2 1 1 2.4000000 2 3 2.1000000 3 3 0.9000000 —————————————————
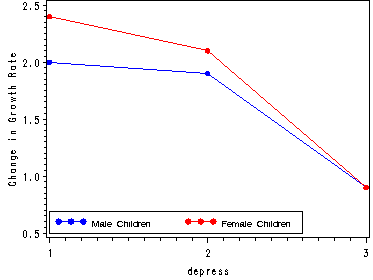
Fig. 22.1, p. 892.
Note: We create two variables for depression means, one for each level of gender. The overlay option in proc gplot lets us plot the two lines in the same graph.
proc means data=growth mean noprint;
class gender depress;
var growth;
output out=temp mean=mout;
run;
data temp;
set temp;
if gender=1 then male=mout;
if gender=2 then female=mout;
run;
goptions reset=all;
symbol1 c=blue v=dot h=.8 i=join;
symbol2 c=red v=dot h=.8 i=join;
axis1 order=(.5 to 2.5 by .5) label=(angle=90 'Change in Growth Rate');
legend1 label=none value=(height=1 font=swiss 'Male Children' 'Female Children' )
position=(left bottom inside) mode=share cborder=black;
proc gplot data=temp;
plot (male female)*depress/ overlay legend=legend1 vaxis=axis;
run;
quit;
Creating the dummy variables to be used in the regression model that will be equivalent to the ANOVA model (22.3), p. 893.
data dummy; set growth; if gender=1 then x1=1; else x1=-1; if depress=1 then x2=1; else if depress=3 then x2=-1; else x2=0; if depress=2 then x3=1; else if depress=3 then x3=-1; else x3=0; x1x2 = x1*x2; x1x3 = x1*x3; run;
Table 22.2, p. 894.
proc print data=dummy; var gender depress rep growth x1 x2 x3 x1x2 x1x3; run;
Obs gender depress rep growth x1 x2 x3 x1x2 x1x3 1 1 1 1 1.4 1 1 0 1 0 2 1 1 2 2.4 1 1 0 1 0 3 1 1 3 2.2 1 1 0 1 0 4 1 2 1 2.1 1 0 1 0 1 5 1 2 2 1.7 1 0 1 0 1 6 1 3 1 0.7 1 -1 -1 -1 -1 7 1 3 2 1.1 1 -1 -1 -1 -1 8 2 1 1 2.4 -1 1 0 -1 0 9 2 2 1 2.5 -1 0 1 0 -1 10 2 2 2 1.8 -1 0 1 0 -1 11 2 2 3 2.0 -1 0 1 0 -1 12 2 3 1 0.5 -1 -1 -1 1 1 13 2 3 2 0.9 -1 -1 -1 1 1 14 2 3 3 1.3 -1 -1 -1 1 1
Table 22.3, p. 895.
proc reg data=dummy; model growth = x1 x2 x3 x1x2 x1x3; model growth = x1 x2 x3; model growth = x2 x3 x1x2 x1x3; model growth = x1 x1x2 x1x3; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: growthAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F Model 5 4.47429 0.89486 5.51 0.0172 Error 8 1.30000 0.16250 Corrected Total 13 5.77429
Root MSE 0.40311 R-Square 0.7749 Dependent Mean 1.64286 Adj R-Sq 0.6342 Coeff Var 24.53731 Parameter Estimates
Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 1.70000 0.11637 14.61 <.0001 x1 1 -0.10000 0.11637 -0.86 0.4152 x2 1 0.50000 0.17776 2.81 0.0227 x3 1 0.30000 0.15756 1.90 0.0934 x1x2 1 -0.10000 0.17776 -0.56 0.5891 x1x3 1 -4.8512E-17 0.15756 -0.00 1.0000
The REG Procedure Model: MODEL2 Dependent Variable: growth
Analysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F Model 3 4.39886 1.46629 10.66 0.0019 Error 10 1.37543 0.13754 Corrected Total 13 5.77429
Root MSE 0.37087 R-Square 0.7618 Dependent Mean 1.64286 Adj R-Sq 0.6903 Coeff Var 22.57456 Parameter Estimates
Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 1.67619 0.09973 16.81 <.0001 x1 1 -0.08571 0.10448 -0.82 0.4311 x2 1 0.46667 0.15418 3.03 0.0127 x3 1 0.32667 0.14035 2.33 0.0422
The REG Procedure Model: MODEL3 Dependent Variable: growth
Analysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F Model 4 4.35429 1.08857 6.90 0.0080 Error 9 1.42000 0.15778 Corrected Total 13 5.77429
Root MSE 0.39721 R-Square 0.7541 Dependent Mean 1.64286 Adj R-Sq 0.6448 Coeff Var 24.17815 Parameter Estimates
Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 1.68889 0.11396 14.82 <.0001 x2 1 0.44444 0.16316 2.72 0.0235 x3 1 0.32778 0.15196 2.16 0.0594 x1x2 1 -0.06667 0.17093 -0.39 0.7056 x1x3 1 -0.01667 0.15408 -0.11 0.9162
The REG Procedure Model: MODEL4 Dependent Variable: growth
Analysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F Model 3 0.28457 0.09486 0.17 0.9124 Error 10 5.48971 0.54897 Corrected Total 13 5.77429
Root MSE 0.74093 R-Square 0.0493 Dependent Mean 1.64286 Adj R-Sq -0.2359 Coeff Var 45.09985 Parameter Estimates
Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 1.62857 0.20873 7.80 <.0001 x1 1 0.01905 0.19924 0.10 0.9257 x1x2 1 0.06667 0.30803 0.22 0.8330 x1x3 1 -0.19333 0.28039 -0.69 0.5062
Testing the interactions, factor A main effects and factor B main effects, p. 894-896.
proc reg data=dummy; model growth = x1 x2 x3 x1x2 x1x3; interactions: test x1x2, x1x3; maina: test x1; mainb: test x2, x3; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: growth
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 5 4.47429 0.89486 5.51 0.0172
Error 8 1.30000 0.16250
Corrected Total 13 5.77429
Root MSE 0.40311 R-Square 0.7749
Dependent Mean 1.64286 Adj R-Sq 0.6342
Coeff Var 24.53731
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 1.70000 0.11637 14.61 <.0001
x1 1 -0.10000 0.11637 -0.86 0.4152
x2 1 0.50000 0.17776 2.81 0.0227
x3 1 0.30000 0.15756 1.90 0.0934
x1x2 1 -0.10000 0.17776 -0.56 0.5891
x1x3 1 -4.8512E-17 0.15756 -0.00 1.0000
The REG Procedure
Model: MODEL1
Test interactions Results for Dependent Variable growth
Mean
Source DF Square F Value Pr > F
Numerator 2 0.03771 0.23 0.7980
Denominator 8 0.16250
The REG Procedure
Model: MODEL1
Test maina Results for Dependent Variable growth
Mean
Source DF Square F Value Pr > F
Numerator 1 0.12000 0.74 0.4152
Denominator 8 0.16250
The REG Procedure
Model: MODEL1
Test mainb Results for Dependent Variable growth
Mean
Source DF Square F Value Pr > F
Numerator 2 2.09486 12.89 0.0031
Denominator 8 0.16250
Table 22.4, p. 897.
proc glm data=growth; class gender depress; model growth = gender depress gender*depress/ss3; run; quit;
The GLM ProcedureClass Level Information
Class Levels Values gender 2 1 2 depress 3 1 2 3
Number of observations 14
The GLM Procedure
Dependent Variable: growth
Sum of Source DF Squares Mean Square F Value Pr > F Model 5 4.47428571 0.89485714 5.51 0.0172 Error 8 1.30000000 0.16250000 Corrected Total 13 5.77428571
R-Square Coeff Var Root MSE growth Mean 0.774864 24.53731 0.403113 1.642857 Source DF Type III SS Mean Square F Value Pr > F gender 1 0.12000000 0.12000000 0.74 0.4152 depress 2 4.18971429 2.09485714 12.89 0.0031 gender*depress 2 0.07542857 0.03771429 0.23 0.7980
Pair-wise comparisons of depress factor level means, p. 901.
Note: Since the model is the same as above all the redundant output has been omitted.
proc glm data=growth; class depress gender; model growth = depress gender depress*gender; lsmeans depress/ pdiff adjust=tukey cl alpha=.1; run; quit;
The GLM Procedure<output omitted>
Least Squares Means Adjustment for Multiple Comparisons: Tukey-Kramer
growth LSMEAN depress LSMEAN Number
1 2.20000000 1 2 2.00000000 2 3 0.90000000 3
Least Squares Means for effect depress Pr > |t| for H0: LSMean(i)=LSMean(j)
Dependent Variable: growth
i/j 1 2 3
1 0.7845 0.0059 2 0.7845 0.0072 3 0.0059 0.0072
growth depress LSMEAN 90% Confidence Limits
1 2.200000 1.767214 2.632786 2 2.000000 1.657852 2.342148 3 0.900000 0.557852 1.242148
Least Squares Means for Effect depress
Difference Simultaneous 90% Between Confidence Limits for i j Means LSMean(i)-LSMean(j)
1 2 0.200000 -0.507807 0.907807 1 3 1.300000 0.592193 2.007807 2 3 1.100000 0.479212 1.720788
Single degree of Freedom test using the growth hormone example, p. 902.
Note: The single degree t-tests are obtained by using the lsmeans statement with the tdiff option. Moreover, since the model is the same as in the two previous proc glm the redundant output has been omitted.proc glm data=growth; class depress gender; model growth = depress gender depress*gender; lsmeans depress/ tdiff stderr; run; quit;<output omitted> The GLM Procedure Least Squares Means growth Standard LSMEAN depress LSMEAN Error Pr > |t| Number 1 2.20000000 0.23273733 <.0001 1 2 2.00000000 0.18399502 <.0001 2 3 0.90000000 0.18399502 0.0012 3 Least Squares Means for Effect depress t for H0: LSMean(i)=LSMean(j) / Pr > |t| Dependent Variable: growth i/j 1 2 3 1 0.67412 4.38178 0.5192 0.0023 2 -0.67412 4.227383 0.5192 0.0029 3 -4.38178 -4.22738 0.0023 0.0029 NOTE: To ensure overall protection level, only probabilities associated with pre-planned comparisons should be used.We cannot reproduce the math score example since the data was not available, p. 906.
Tests of the null hypothesis in (22.24a) first using proc glm and then using two regression models, p. 907-908.
Note: In the code for proc glm the order of the categorical variables in the class statement is very important and it has to match the order to the interaction. If the interaction is gender*depress then the class statement has to be class gender depress. It is rather tricky figuring out the order of the coefficients that should be entered into the contrast statement. When the interaction is gender*depress the coefficients in the contrast statement are those of the cell means in the following order: mu11 mu12 mu13 mu21 mu22 mu23 where the first index is for the gender factor and the second index is for the depress factor. In the second version of the code where the order of the interaction was switched the coefficients in the contrast statement are those of the cell means in the following order: mu11 mu21 mu12 mu22 mu13 mu23 (where the first index is for the gender factor and the second index is for the depress factor).proc glm data=growth; class gender depress; model growth = gender*depress; contrast 'contrast' gender*depress .666 -.666 0 .333 -.333 0, gender*depress .666 0 -.666 .333 0 -.333; run; quit; proc glm data=growth; class depress gender ; model growth = depress*gender; contrast 'contrast' depress*gender .666 .333 -.666 -.333 0 0, depress*gender .666 .333 0 0 -.666 -.333; run; quit;The GLM ProcedureClass Level Information
Class Levels Values gender 2 1 2 depress 3 1 2 3
Number of observations 14
The GLM Procedure Dependent Variable: growth
Sum of Source DF Squares Mean Square F Value Pr > F
Model 5 4.47428571 0.89485714 5.51 0.0172 Error 8 1.30000000 0.16250000 Corrected Total 13 5.77428571 R-Square Coeff Var Root MSE growth Mean
0.774864 24.53731 0.403113 1.642857
Source DF Type I SS Mean Square F Value Pr > F gender*depress 5 4.47428571 0.89485714 5.51 0.0172 Source DF Type III SS Mean Square F Value Pr > F gender*depress 5 4.47428571 0.89485714 5.51 0.0172
Contrast DF Contrast SS Mean Square F Value Pr > F contrast 2 3.45428571 1.72714286 10.63 0.0056
The GLM Procedure
Class Level Information
Class Levels Values depress 3 1 2 3 gender 2 1 2
Number of observations 14
The GLM Procedure Dependent Variable: growth
Sum of Source DF Squares Mean Square F Value Pr > F
Model 5 4.47428571 0.89485714 5.51 0.0172 Error 8 1.30000000 0.16250000 Corrected Total 13 5.77428571
R-Square Coeff Var Root MSE growth Mean 0.774864 24.53731 0.403113 1.642857
Source DF Type I SS Mean Square F Value Pr > F depress*gender 5 4.47428571 0.89485714 5.51 0.0172
Source DF Type III SS Mean Square F Value Pr > F depress*gender 5 4.47428571 0.89485714 5.51 0.0172 Contrast DF Contrast SS Mean Square F Value Pr > F contrast 2 3.45428571 1.72714286 10.63 0.0056
Creating the dummy variables to get the regression model that will supply us with the value of SSE(F), p. 908.
data dummyx; set growth; x1 = 0; if gender=1 and depress=1 then x1=1; x2 = 0; if gender=1 and depress=2 then x2=1; x3 = 0; if gender=1 and depress=3 then x3=1; x4 = 0; if gender=2 and depress=1 then x4=1; x5 = 0; if gender=2 and depress=2 then x5=1; x6 = 0; if gender=2 and depress=3 then x6=1; run;Running the regression model and using ODS to create two macro variables, one for SSE(F) and one for DF_F. In order to check that we have the correct macro variable we use a put statement to look at the macro variables in the log file.
ods listing close; ods output anova=full; proc reg data = dummyx; model growth = x1-x6 / noint; run; quit; ods listing; data _null_; set full; if source='Error' then call symput('fullss', ss); if source='Error' then call symput('fulldf', df); run; %put here are the values &fullss and &fulldf; /* check values in the log file */Creating the dummy variables for the reduced regression model, p. 909 and running the second regression model and using ODS to create two macro variables, one for SSE(R) and one for DF_R. In order to check that we have the correct macro variable we use a put statement to look at the macro variables in the log file.
data dummyz; set dummyx; z1 = x1 - 2*x4; z2 = x2 +2*x4 +2*x6; z3 = x3 -2*x6; z4 = x4 +x5+x6; run; ods listing close; ods output anova=reduced; proc reg data=dummyz; model growth = z1-z4/ noint; run; quit; ods listing; data _null_; set reduced; if source='Error' then call symput('reducedss', ss); if source='Error' then call symput('reduceddf', df); run; %put here are the values &reducedss and &reduceddf; /* check values in log file */Finally, we use all the values that were extracted from the two regression models in an F-test, p. 909.
data temp; SSE_R= &reducedss; SSE_F= &fullss; DF_R = &reduceddf; DF_F = &fulldf; Fstar = ( (&reducess - &fullss)/( &reduceddf - &fulldf) ) /( &fullss/ &fulldf); p_value = 1 - cdf( 'F', fstar, &reduceddf - &fulldf, &fulldf); run; proc print data=temp; run;Obs SSE_R SSE_F DF_R DF_F Fstar p_value1 4.75429 1.3 10 8 10.6286 .005590264
Repeating the same test using SSA, p. 914.
Note: First we use proc glm to obtain SSA and the DF_A and store them as macro variables. Then we will use the data set dummy and re-run the full regression model including interactions in order to obtain the SSE(F) and df_F as presented in table 22.3a, p. 895 and store them as macro variables. Finally, we use all the values that we extracted in an F-test.ods listing close; ods output ModelANOVA=ssa; proc glm data=growth; class gender depress; model growth = gender depress/ ss1; run; quit; ods listing; data _null_; set ssa; if source='gender' then call symput('ssa', ss); if source='gender' then call symput('dfa', df); run; %put here are the values &ssa and &dfa; /*check the values in the log file */ ods listing close; ods output anova=anova; proc reg data=dummy; model growth = x1 x2 x3 x1x2 x1x3; run; quit; ods listing; data _null_; set anova; if source='Error' then call symput('fullss', ss); if source='Error' then call symput('fulldf', df); run; %put here are the values &fullss and &fulldf; /* check the values in the log file */ data temp; SSA = &ssa; DF_A = &dfa; SSE_F = &fullss; DF_F = &fulldf; Fstar = (&ssa/&dfa)/( &fullss/ &fulldf); p_value = 1 - cdf( 'F', Fstar, &dfa, &fulldf); run; proc print data=temp; run;Obs SSA DF_A SSE_F DF_F Fstar p_value1 .002857143 1 1.3 8 0.017582 0.89779