Inputting table 23.4a, p. 943.
data stress;
input exercise gender fat smoking rep;
label gender='1=male, 2=female'
fat='1=low fat, 2=high fat'
smoking='1=Light, 2=heavy';
cards;
24.1 1 1 1 1
29.2 1 1 1 2
24.6 1 1 1 3
20.0 2 1 1 1
21.9 2 1 1 2
17.6 2 1 1 3
14.6 1 2 1 1
15.3 1 2 1 2
12.3 1 2 1 3
16.1 2 2 1 1
9.3 2 2 1 2
10.8 2 2 1 3
17.6 1 1 2 1
18.8 1 1 2 2
23.2 1 1 2 3
14.8 2 1 2 1
10.3 2 1 2 2
11.3 2 1 2 3
14.9 1 2 2 1
20.4 1 2 2 2
12.8 1 2 2 3
10.1 2 2 2 1
14.4 2 2 2 2
6.1 2 2 2 3
;
run;
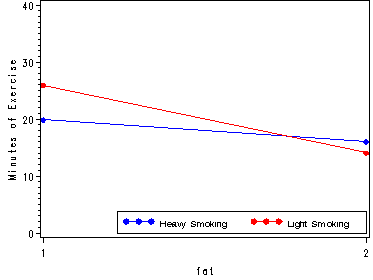
Table 23.4b, p. 943. The cell means and the factor means.
Note: It would be possible to obtain all the means by using multiple proc means but the lsmeans statement in proc glm is actually more flexible and allows you to obtain all the means in a single statement. The bars is a special notation which indicates that all the interactions should be included even the three-way interaction.
ods output GLM.LSMEANS.gender_fat_smoking.LSMeans=temp;
ods listing close;
proc glm data= stress;
class gender fat smoking;
model exercise = gender|fat|smoking ;
lsmeans gender|fat|smoking;
run;
quit;
proc print data=temp;
run;
ods listing;
data temp1;
set temp;
if gender=1 then
if smoking=2 then heavy_m= exerciseLSMean;
else if smoking=1 then light_m=exerciseLSMean;
if gender=2 then
if smoking=2 then heavy_f= exerciseLSMean;
else if smoking=1 then light_f=exerciseLSMean;
if smoking=1 then
if fat=2 then light_high = exerciseLSMean;
else if fat=1 then light_low = exerciseLSMean;
if smoking=2 then
if fat=1 then heavy_high = exerciseLSMean;
else if fat=2 then heavy_low = exerciseLSMean;
run;
goptions reset=all;
symbol1 v=dot c=blue h=.8 i=join;
symbol2 v=dot c=red h=.8 i=join;
axis1 order=(0 to 40 by 10) label=(angle=90 'Minutes of Exercise');
legend1 label=none value=(height=1 font=swiss 'Heavy Smoking' 'Light Smoking' )
position=(bottom right inside) mode=share cborder=black;
legend2 label=none value=(height=1 font=swiss 'Low Fat' 'High Fat' )
position=(bottom right inside) mode=share cborder=black;
proc gplot data = temp1;
plot (heavy_m light_m)*fat/ overlay vaxis=axis1 legend=legend1 ;
run;
filename outfile 'c:sas2htmhttps://stats.idre.ucla.edu/wp-content/uploads/2016/02/alsm23_2.gif';
goptions gsfmode=replace gsfname=outfile device=gif373;
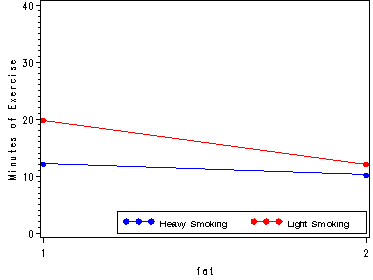
plot (heavy_f light_f)*fat /overlay vaxis=axis1 legend=legend1 ;
run;
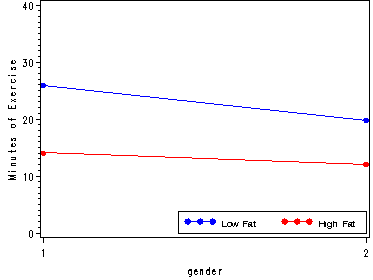
plot (light_low light_high)*gender/ overlay vaxis=axis1 legend=legend2 ;
run;
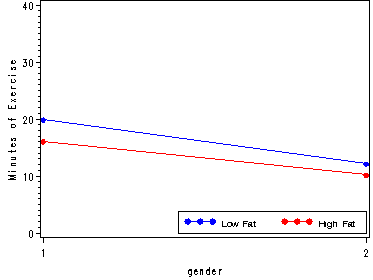
plot (heavy_high heavy_low)*gender / overlay vaxis=axis1 legend=legend2 ;
run;
quit;
goptions reset=all;
exercise Obs Effect gender fat smoking LSMean1 gender_fat_smoking 1 1 1 25.9666667 2 gender_fat_smoking 1 1 2 19.8666667 3 gender_fat_smoking 1 2 1 14.0666667 4 gender_fat_smoking 1 2 2 16.0333333 5 gender_fat_smoking 2 1 1 19.8333333 6 gender_fat_smoking 2 1 2 12.1333333 7 gender_fat_smoking 2 2 1 12.0666667 8 gender_fat_smoking 2 2 2 10.2000000
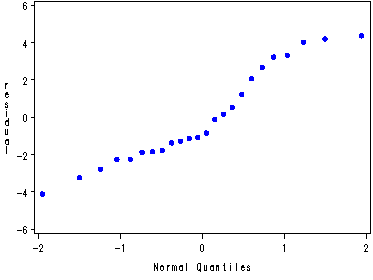
Fig. 23.7 and 23.8, p. 945.
proc glm data=stress; class gender fat smoking; model exercise = gender|fat|smoking; output out=temp r=residual; run; quit; symbol v=dot c=blue h=.8; proc capability data=temp noprint; qqplot residual; run;
The GLM ProcedureClass Level Information
Class Levels Values gender 2 1 2 fat 2 1 2 smoking 2 1 2
Number of observations 24
The GLM Procedure
Dependent Variable: exercise Sum of Source DF Squares Mean Square F Value Pr > F Model 7 588.5829167 84.0832738 9.01 0.0002 Error 16 149.3666667 9.3354167 Corrected Total 23 737.9495833
R-Square Coeff Var Root MSE exercise Mean 0.797592 18.77833 3.055391 16.27083
Source DF Type I SS Mean Square F Value Pr > F gender 1 176.5837500 176.5837500 18.92 0.0005 fat 1 242.5704167 242.5704167 25.98 0.0001 gender*fat 1 13.6504167 13.6504167 1.46 0.2441 smoking 1 70.3837500 70.3837500 7.54 0.0144 gender*smoking 1 11.0704167 11.0704167 1.19 0.2923 fat*smoking 1 72.4537500 72.4537500 7.76 0.0132 gender*fat*smoking 1 1.8704167 1.8704167 0.20 0.6604Source DF Type III SS Mean Square F Value Pr > F gender 1 176.5837500 176.5837500 18.92 0.0005 fat 1 242.5704167 242.5704167 25.98 0.0001 gender*fat 1 13.6504167 13.6504167 1.46 0.2441 smoking 1 70.3837500 70.3837500 7.54 0.0144 gender*smoking 1 11.0704167 11.0704167 1.19 0.2923 fat*smoking 1 72.4537500 72.4537500 7.76 0.0132 gender*fat*smoking 1 1.8704167 1.8704167 0.20 0.6604
Estimation of Contrasts of Treatment means, p. 947.
First we obtain the relevant datasets from the output of the proc glm using ods. Then we create a macro variable for the degrees of freedom that we need in order to obtain the Bonferroni multiple for a 95% family confidence coefficient. Finally, we get the confidence intervals for each of the three contrasts, p. 948.
ods output Estimates=temp;
ods output OverallANOVA=anova;
proc glm data=stress;
class gender fat smoking;
model exercise = gender|fat|smoking;
estimate 'L1' smoking 1 -1 fat*smoking 1 -1 0 0;
estimate 'L2' smoking 1 -1 fat*smoking 0 0 1 -1;
estimate 'L3' gender 1 -1;
run;
quit;
data _null_;
set anova;
if source='Error' then call symput('Df', DF);
run;
%put here is the df we should use &df;
data temp;
set temp;
drop dependent tvalue probt;
B = tinv( 1- (.05/6), &df);
lower = estimate - B*stderr;
upper = estimate + B*stderr;
run;
proc print data=temp;
run;
The GLM ProcedureClass Level Information
Class Levels Values gender 2 1 2 fat 2 1 2 smoking 2 1 2
Number of observations 24
The GLM Procedure
Dependent Variable: exercise Sum of Source DF Squares Mean Square F Value Pr > F Model 7 588.5829167 84.0832738 9.01 0.0002 Error 16 149.3666667 9.3354167 Corrected Total 23 737.9495833
R-Square Coeff Var Root MSE exercise Mean 0.797592 18.77833 3.055391 16.27083
Source DF Type I SS Mean Square F Value Pr > F gender 1 176.5837500 176.5837500 18.92 0.0005 fat 1 242.5704167 242.5704167 25.98 0.0001 gender*fat 1 13.6504167 13.6504167 1.46 0.2441 smoking 1 70.3837500 70.3837500 7.54 0.0144 gender*smoking 1 11.0704167 11.0704167 1.19 0.2923 fat*smoking 1 72.4537500 72.4537500 7.76 0.0132 gender*fat*smoking 1 1.8704167 1.8704167 0.20 0.6604
Source DF Type III SS Mean Square F Value Pr > F gender 1 176.5837500 176.5837500 18.92 0.0005 fat 1 242.5704167 242.5704167 25.98 0.0001 gender*fat 1 13.6504167 13.6504167 1.46 0.2441 smoking 1 70.3837500 70.3837500 7.54 0.0144 gender*smoking 1 11.0704167 11.0704167 1.19 0.2923 fat*smoking 1 72.4537500 72.4537500 7.76 0.0132 gender*fat*smoking 1 1.8704167 1.8704167 0.20 0.6604
Standard Parameter Estimate Error t Value Pr > |t| L1 6.90000000 1.76403105 3.91 0.0012 L2 -0.05000000 1.76403105 -0.03 0.9777 L3 5.42500000 1.24735832 4.35 0.0005
Obs Parameter Estimate StdErr B lower upper1 L1 6.90000000 1.76403105 2.67303 2.18469 11.6153 2 L2 -0.05000000 1.76403105 2.67303 -4.76531 4.6653 3 L3 5.42500000 1.24735832 2.67303 2.09077 8.7592
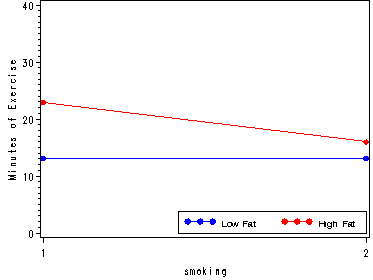
The effects of Body Fat and Smoking History, fig. 23.9b, p. 949.
ods output GLM.LSMEANS.fat_smoking.LSMeans=temp; ods listing close; proc glm data= stress; class fat smoking; model exercise = fat smoking fat*smoking ; lsmeans fat smoking fat*smoking; run; quit; ods listing; data temp1; set temp; if fat=1 then low = exerciseLSMean; else if fat=2 then high = exerciseLSMean; run; goptions reset=all; symbol1 v=dot c=blue h=.8 i=join; symbol2 v=dot c=red h=.8 i=join; axis1 order=(0 to 40 by 10) label=(angle=90 'Minutes of Exercise'); legend1 label=none value=(height=1 font=swiss 'Low Fat' 'High Fat' ) position=(bottom right inside) mode=share cborder=black; proc gplot data = temp1; plot (high low)*smoking/ overlay vaxis=axis1 legend=legend1 ; run; quit; goptions reset=all;
Creating the Stress data with missing values and generating the indicator variables, table 23.5, p. 950.
data missing; set stress; if gender=1 and fat=1 and smoking=1 and rep=3 then delete; if gender=2 and fat=2 and smoking=1 and rep=2 then delete; y = exercise; x1 = 1; if gender=2 then x1 = -1; x2 = 1; if fat=2 then x2 = -1; x3 = 1; if smoking=2 then x3 = -1; x12 = x1*x2; x13 = x1*x3; x23 = x2*x3; x123 = x1*x2*x3; run; proc print data=missing; run;
Obs exercise gender fat smoking rep y x1 x2 x3 x12 x13 x23 x1231 24.1 1 1 1 1 24.1 1 1 1 1 1 1 1 2 29.2 1 1 1 2 29.2 1 1 1 1 1 1 1 3 20.0 2 1 1 1 20.0 -1 1 1 -1 -1 1 -1 4 21.9 2 1 1 2 21.9 -1 1 1 -1 -1 1 -1 5 17.6 2 1 1 3 17.6 -1 1 1 -1 -1 1 -1 6 14.6 1 2 1 1 14.6 1 -1 1 -1 1 -1 -1 7 15.3 1 2 1 2 15.3 1 -1 1 -1 1 -1 -1 8 12.3 1 2 1 3 12.3 1 -1 1 -1 1 -1 -1 9 16.1 2 2 1 1 16.1 -1 -1 1 1 -1 -1 1 10 10.8 2 2 1 3 10.8 -1 -1 1 1 -1 -1 1 11 17.6 1 1 2 1 17.6 1 1 -1 1 -1 -1 -1 12 18.8 1 1 2 2 18.8 1 1 -1 1 -1 -1 -1 13 23.2 1 1 2 3 23.2 1 1 -1 1 -1 -1 -1 14 14.8 2 1 2 1 14.8 -1 1 -1 -1 1 -1 1 15 10.3 2 1 2 2 10.3 -1 1 -1 -1 1 -1 1 16 11.3 2 1 2 3 11.3 -1 1 -1 -1 1 -1 1 17 14.9 1 2 2 1 14.9 1 -1 -1 -1 -1 1 1 18 20.4 1 2 2 2 20.4 1 -1 -1 -1 -1 1 1 19 12.8 1 2 2 3 12.8 1 -1 -1 -1 -1 1 1 20 10.1 2 2 2 1 10.1 -1 -1 -1 1 1 1 -1 21 14.4 2 2 2 2 14.4 -1 -1 -1 1 1 1 -1 22 6.1 2 2 2 3 6.1 -1 -1 -1 1 1 1 -1
Testing factor A (Gender) by dropping x1 from the full model and regressing y on the variables in column 3-8, p. 950.
proc reg data=missing; model y = x1-x3 x12 x13 x23 x123; model y = x2 x3 x12 x13 x23 x123; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: yAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F Model 7 484.81485 69.25926 7.18 0.0009 Error 14 135.08333 9.64881 Corrected Total 21 619.89818
Root MSE 3.10625 R-Square 0.7821 Dependent Mean 16.20909 Adj R-Sq 0.6731 Coeff Var 19.16365
Parameter EstimatesParameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 16.52917 0.67252 24.58 <.0001 x1 1 2.62500 0.67252 3.90 0.0016 x2 1 3.09167 0.67252 4.60 0.0004 x3 1 1.97083 0.67252 2.93 0.0110 x12 1 1.01250 0.67252 1.51 0.1544 x13 1 -0.76667 0.67252 -1.14 0.2734 x23 1 1.65000 0.67252 2.45 0.0279 x123 1 0.53750 0.67252 0.80 0.4375
The REG Procedure Model: MODEL2 Dependent Variable: y
Analysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F Model 6 337.81485 56.30247 2.99 0.0397 Error 15 282.08333 18.80556 Corrected Total 21 619.89818
Root MSE 4.33654 R-Square 0.5450 Dependent Mean 16.20909 Adj R-Sq 0.3629 Coeff Var 26.75374
Parameter EstimatesParameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 16.52917 0.93889 17.61 <.0001 x2 1 2.80000 0.93307 3.00 0.0090 x3 1 1.97083 0.93889 2.10 0.0531 x12 1 1.01250 0.93889 1.08 0.2979 x13 1 -1.05833 0.93307 -1.13 0.2745 x23 1 1.35833 0.93307 1.46 0.1661 x123 1 0.53750 0.93889 0.57 0.5755