Applied Linear Statistical Models by Neter, Kutner, et. al. Chapter 4: Simultaneous Inferences and Other Topics in Regression Analysis

options nocenter nodate;

Inputting the Toluca Company data.

data ch1tab01;
  input x y;
  label x = 'Lot Size'
        y = 'Work Hrs';
cards;
   80  399
   30  121
   50  221
   90  376
   70  361
   60  224
  120  546
   80  352
  100  353
   50  157
   40  160
   70  252
   90  389
   20  113
  110  435
  100  420
   30  212
   50  268
   90  377
  110  421
   30  273
   90  468
   40  244
   80  342
   70  323
;
run;

Example of 90% Confidence Intervals for the regression parameter estimates, p. 154.

proc reg data = ch1tab01;
  model y = x/ clb;
run;
quit;

The REG Procedure
Model: MODEL1
Dependent Variable: y Work Hrs
                             Analysis of Variance
                                    Sum of           Mean
Source                   DF        Squares         Square    F Value    Pr > F
Model                     1         252378         252378     105.88    <.0001
Error                    23          54825     2383.71562
Corrected Total          24         307203
Root MSE             48.82331    R-Square     0.8215
Dependent Mean      312.28000    Adj R-Sq     0.8138
Coeff Var            15.63447
                                      Parameter Estimates
                            Parameter     Standard
Variable   Label      DF     Estimate        Error  t Value  Pr > |t|    95% Confidence Limits
Intercept  Intercept   1     62.36586     26.17743     2.38    0.0259      8.21371    116.51801
x          Lot Size    1      3.57020      0.34697    10.29    <.0001      2.85244      4.28797

Using the Working-Hotelling procedure to obtain a family of estimates and confidence
intervals for mean working hours when X = 30, 65, 100 with a family confidence coefficient
of 0.90, p. 156-157.

data extra;
  input x y; 
cards;
  30 .
  65 .
 100 .
;
run;
data temp;
  set ch1tab01 extra;
run;
ods listing close;
ods output anova=out;
proc reg data = temp;
  model y = x/ alpha=.1;
  output out=temp1 p=yhat stdi=stdi;
run;
quit;
ods listing;
data _null_;
  set out;
  if source = 'Error' then do;
  call symput ('mse', ms);
  call symput ('df', df );
  end;
run;
%put &mse &df; /* To see the value of MSE and df in the log file. */ 
data temp2;
  set temp1;
  if y=.;
  syh = sqrt( (stdi)**2 - &mse );
  f = finv(.90, 2, &df); 
  w = sqrt( 2*f );
  lower = yhat - w*syh;
  upper = yhat + w*syh;
run;
proc print data = temp2;
  var x yhat syh f w lower upper;
run; 
Obs     x       yhat       syh         f          w        lower      upper
 1      30    169.472    16.9697    2.54929    2.25800    131.154    207.790
 2      65    294.429     9.9176    2.54929    2.25800    272.035    316.823
 3     100    419.386    14.2723    2.54929    2.25800    387.159    451.613

Using the Bonferroni procedure to obtain a family of estimates and confidence
intervals for mean working hours when X = 30, 65, 100 with a family confidence coefficient
of 0.90, p. 157.
data extra;
  input x y; 
cards;
  30 .
  65 .
 100 .
;
run;
data temp;
  set ch1tab01 extra;
run;
ods listing close;
ods output anova=out;
proc reg data = temp;
  model y = x/ alpha=.1;
  output out=temp1 p=yhat stdi=stdi;
run;
quit;
ods listing;
data _null_;
  set out;
  if source = 'Error' then do;
  call symput ('mse', ms);
  call symput ('df', df );
  end;
run;
%put &mse &df; /* To see the value of MSE and df in the log file. */ 
data temp2;
  set temp1;
  if y=.;
  syh = sqrt( (stdi)**2 - &mse );
  B = tinv( 1- (.1 /(2*3)), &df); 
  lower = yhat - B*syh;
  upper = yhat + B*syh;
run;
proc print data = temp2;
  var x yhat syh B lower upper;
run; 
Obs     x       yhat       syh         B        lower      upper
 1      30    169.472    16.9697    2.26373    131.057    207.887
 2      65    294.429     9.9176    2.26373    271.978    316.880
 3     100    419.386    14.2723    2.26373    387.077    451.695

Simultaneous Prediction intervals for new observations, p. 158-159.
data extra;
  input x y; 
cards;
  80 .
 100 .
;
run;
data temp;
  set ch1tab01 extra;
run;
proc reg data = temp noprint;
  model y = x/ alpha=.1;
  output out=temp1 p=yhat stdi=spred;
run;
quit;
data temp2;
  set temp1;
  if y=.;
  s = sqrt( 2*finv(.95, 2, 23) ); 
  B = tinv( 1 - (.05/(2*2)), 23) ;
  lowers = yhat - s*spred;
  uppers = yhat + s*spred;
  lowerb = yhat - b*spred;
  upperb = yhat + b*spred;
run;
proc print data = temp2;
  var x yhat spred b lowerb upperb s lowers uppers;
run; 
Obs    x      yhat     spred       B       lowerb    upperb      s       lowers    uppersc
 1     80   347.982   49.9110   2.39788   228.302   467.662   2.61615   217.407   478.557
 2    100   419.386   50.8666   2.39788   297.414   541.358   2.61615   286.311   552.461

Inputting the Warehouse data, table 4.2, p. 161.
data ch4tab02;
  input x y;
  label x = 'Work'
        y = 'Labor';
cards;
   20  114
  196  921
  115  560
   50  245
  122  575
  100  475
   33  138
  154  727
   80  375
  147  670
  182  828
  160  762
;
run;
Creating the interaction between X and Y, the X^2 and the predicted Y-hat values. The rest
of table 4.2, p. 161.
data ch4tab02;
  set ch4tab02;
  xy = x*y;
  xsq = x**2;
run;
proc reg data = ch4tab02 noprint;
  model y = x /noint;
  output out= temp p=yhat r=e;
run;
proc print data = temp (obs = 5);
run;
Obs     x      y       xy       xsq       yhat        e
  1     20    114      2280      400     93.705    20.2945
  2    196    921    180516    38416    918.314     2.6863
  3    115    560     64400    13225    538.807    21.1935
  4     50    245     12250     2500    234.264    10.7363
  5    122    575     70150    14884    571.603     3.3966

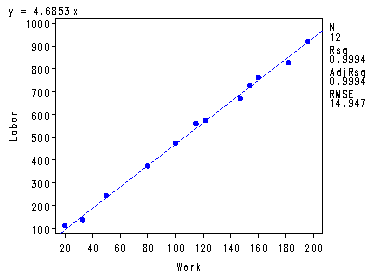
Fig. 4.1 and calculations on p. 162.
goptions reset = all;
 
symbol v=dot h=.8 c=blue;
proc reg data = temp;
  model y = x/ noint clb;
  plot y*x;
run;
quit;

The REG Procedure
Model: MODEL1
Dependent Variable: y Labor
NOTE: No intercept in model. R-Square is redefined.
                             Analysis of Variance
                                    Sum of           Mean
Source                   DF        Squares         Square    F Value    Pr > F
Model                     1        4191980        4191980    18762.5    <.0001
Error                    11     2457.65933      223.42358
Uncorrected Total        12        4194438
Root MSE             14.94736    R-Square     0.9994
Dependent Mean      532.50000    Adj R-Sq     0.9994
Coeff Var             2.80702
                                      Parameter Estimates
                            Parameter     Standard
Variable   Label      DF     Estimate        Error  t Value  Pr > |t|    95% Confidence Limits
x          Work        1      4.68527      0.03421   136.98    <.0001      4.60999      4.76056

The Calibration example p. 168 was not reproduced.