Section 11.1
Regression analysis in the middle of page 269 using the davis data file. First create a dataset with a dummy variable called female and an interaction regressor measwt as the product of measured weight and female. Run regression on them.
data davisIn; /*A dataset with the interaction variable and a subject variable*/
set davis;
measwt_f = measwt * (1-male);
female=1-male;
drop male;
run;
proc reg data=davisIn;
model reptwt=measwt female measwt_f;
run;
quit;
The REG Procedure
Model: MODEL1
Dependent Variable: reptwt
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 30655 10218 470.41 <.0001
Error 179 3888.25423 21.72209
Corrected Total 182 34543
Root MSE 4.66070 R-Square 0.8874
Dependent Mean 65.62295 Adj R-Sq 0.8856
Coeff Var 7.10224
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 1.35864 3.27719 0.41 0.6789
measwt 1 0.98982 0.04260 23.24 <.0001
female 1 39.96412 3.92932 10.17 <.0001
measwt_f 1 -0.72536 0.05598 -12.96 <.0001
Now we fix the error in case 12 of the dataset. We keep the dataset with the error as davisIn and call our new fixed dataset as davis_co.
data davis_co;
set davisIn;
if _n_=12 then do
temp=measht;
measht=measwt;
measwt=temp;
measwt_f=temp;
end;
drop temp;
run;
proc reg data=davis_co ;
model reptwt=measwt female measwt_f;
run;
quit;
The REG Procedure
Model: MODEL1
Dependent Variable: reptwt
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 33642 11214 2228.78 <.0001
Error 179 900.63897 5.03150
Corrected Total 182 34543
Root MSE 2.24310 R-Square 0.9739
Dependent Mean 65.62295 Adj R-Sq 0.9735
Coeff Var 3.41817
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 1.35864 1.57725 0.86 0.3902
measwt 1 0.98982 0.02050 48.28 <.0001
female 1 1.98252 2.45028 0.81 0.4195
measwt_f 1 -0.05668 0.03845 -1.47 0.1422
To get the formula on page 270, we need to create a dataset containing the dummy variable of female and a new interaction regressor reptwt_f. Then we run regression of reported weight on measured weight. We run them on both corrected and uncorrected dataset.
Corrected dataset
data davis_co1;
set davis;
reptwt_f=reptwt*(1-male);
female=1-male;
if subject=12 then do
temp=measwt;
measwt=measht;
measht=temp;
end;
drop male temp;
run;
proc reg data=davis_co1;
model measwt=reptwt female reptwt_f;
run;
quit;
The REG Procedure
Model: MODEL1
Dependent Variable: measwt
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 31722 10574 2082.30 <.0001
Error 179 908.96214 5.07800
Corrected Total 182 32631
Root MSE 2.25344 R-Square 0.9721
Dependent Mean 65.62842 Adj R-Sq 0.9717
Coeff Var 3.43364
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 1.79428 1.57989 1.14 0.2576
reptwt 1 0.96892 0.02038 47.55 <.0001
female 1 -0.01678 2.47955 -0.01 0.9946
reptwt_f 1 0.00831 0.03917 0.21 0.8323
Now on uncorrected dataset.
data davisIn1;
set davis;
reptwt_f=reptwt*(1-male);
female=1-male;
drop male;
run;
proc reg data=davisIn1;
model measwt=reptwt female reptwt_f;
run;
quit;
The REG Procedure
Model: MODEL1
Dependent Variable: measwt
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 29786 9928.79278 139.07 <.0001
Error 179 12779 71.39350
Corrected Total 182 42566
Root MSE 8.44947 R-Square 0.6998
Dependent Mean 66.22404 Adj R-Sq 0.6947
Coeff Var 12.75891
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 1.79428 5.92394 0.30 0.7623
reptwt 1 0.96892 0.07641 12.68 <.0001
female 1 2.07421 9.29727 0.22 0.8237
reptwt_f 1 -0.00953 0.14685 -0.06 0.9484
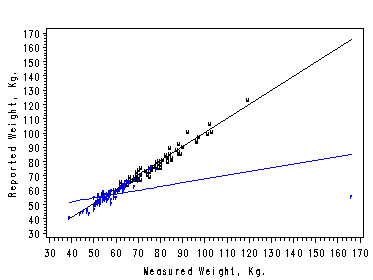
To produce Figure 11.2. on page 270, we first create a dataset that contains two new variables freptwt and mreptwt for reported weight on female and male respectively. Then we run proc glm on the dataset and output the predicted values for both female an male group. Then we use SAS proc gplot to render the plot
data davisPr; set davis; if male=1 then mreptwt=reptwt; if male=0 then freptwt=reptwt; output; run; /*dataset created*/ proc glm data=davisPr; model mreptwt freptwt =measwt; output out=dvsOut p=pm pf; run; quit; symbol1 c=black i=none v='M' height=0.5; symbol2 c=black i=join v=none height=1.5; symbol3 c=blue i=none v='F' height=0.5; symbol4 c=blue i=join v=none height=1.5; axis1 label=(r=0 a=90); filename outfiles 'https://stats.idre.ucla.edu/wp-content/uploads/2016/02/chp11Fig1.gif'; goptions gsfname=outfiles dev=gif373; proc sort data=dvsOut; by measwt; run; proc gplot data=dvsOut; plot mreptwt*measwt=1 pm*measwt=2 freptwt*measwt=3 pf*measwt=4 /overlay vaxis=axis1; label measwt='Measured Weight, Kg.'; label mreptwt='Reported Weight, Kg.'; run; quit;
Section 11.2
Page 271, make hat diagonal (leverage) and show largest values.
proc reg data=davisIn ;
model reptwt=measwt female measwt_f;
output out=dvsLev p=pr h=lev;/* p for predicted h for leverage*/;
run;
quit;
proc univariate data=dvsLev;
var lev;
run;
proc print data=dvsLev;
where lev ge 0.7;
run;
The REG Procedure
Model: MODEL1
Dependent Variable: reptwt
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 30655 10218 470.41 <.0001
Error 179 3888.25423 21.72209
Corrected Total 182 34543
Root MSE 4.66070 R-Square 0.8874
Dependent Mean 65.62295 Adj R-Sq 0.8856
Coeff Var 7.10224
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 1.35864 3.27719 0.41 0.6789
measwt 1 0.98982 0.04260 23.24 <.0001
female 1 39.96412 3.92932 10.17 <.0001
measwt_f 1 -0.72536 0.05598 -12.96 <.0001
The UNIVARIATE Procedure
Variable: lev (Leverage)
Moments
N 200 Sum Weights 200
Mean 0.0212232 Sum Observations 4.2446399
Std Deviation 0.0514178 Variance 0.00264379
Skewness 12.5535875 Kurtosis 168.15714
Uncorrected SS 0.61619913 Corrected SS 0.52611429
Coeff Variation 242.271682 Std Error Mean 0.00363579
Basic Statistical Measures
Location Variability
Mean 0.021223 Std Deviation 0.05142
Median 0.013143 Variance 0.00264
Mode 0.010224 Range 0.70428
Interquartile Range 0.00754
NOTE: The mode displayed is the smallest of 3 modes with a count of 8.
Tests for Location: Mu0=0
Test -Statistic- -----p Value------
Student's t t 5.837304 Pr > |t| <.0001
Sign M 100 Pr >= |M| <.0001
Signed Rank S 10050 Pr >= |S| <.0001
Quantiles (Definition 5)
Quantile Estimate
100% Max 0.71418565
99% 0.12002413
95% 0.04561218
90% 0.02856951
75% Q3 0.01856466
50% Median 0.01314321
25% Q1 0.01102743
10% 0.01014961
5% 0.00993016
1% 0.00990671
0% Min 0.00990671
The UNIVARIATE Procedure
Variable: lev (Leverage)
Extreme Observations
-------Lowest------- ------Highest------
Value Obs Value Obs
0.00990671 188 0.0645111 30
0.00990671 159 0.0687759 54
0.00990671 28 0.0732077 97
0.00990671 2 0.1668405 21
0.00993016 193 0.7141856 12
Obs subject sex measwt measht reptwt reptht measwt_f female pr lev
12 12 F 166 57 56 163 166 1 85.2230 0.71419
With the error corrected:
proc reg data=davis_co;
model measwt=reptwt female measwt_f;
output out=dvs_coH p=pm h=lev;
run;
quit;
proc univariate data=dvs_coH;
var lev;
run;
The REG Procedure
Model: MODEL1
Dependent Variable: measwt
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 31777 10592 2220.97 <.0001
Error 179 853.69481 4.76924
Corrected Total 182 32631
Root MSE 2.18386 R-Square 0.9738
Dependent Mean 65.62842 Adj R-Sq 0.9734
Coeff Var 3.32761
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 4.14385 1.50728 2.75 0.0066
reptwt 1 0.93823 0.01943 48.28 <.0001
female 1 -7.27862 2.32718 -3.13 0.0021
measwt_f 1 0.12450 0.03650 3.41 0.0008
The UNIVARIATE Procedure
Variable: lev (Leverage)
Moments
N 183 Sum Weights 183
Mean 0.02185792 Sum Observations 4
Std Deviation 0.0193944 Variance 0.00037614
Skewness 4.83073039 Kurtosis 33.3623499
Uncorrected SS 0.15588965 Corrected SS 0.06845796
Coeff Variation 88.729365 Std Error Mean 0.00143368
Basic Statistical Measures
Location Variability
Mean 0.021858 Std Deviation 0.01939
Median 0.015604 Variance 0.0003761
Mode 0.015604 Range 0.18047
Interquartile Range 0.00864
Tests for Location: Mu0=0
Test -Statistic- -----p Value------
Student's t t 15.24608 Pr > |t| <.0001
Sign M 91.5 Pr >= |M| <.0001
Signed Rank S 8418 Pr >= |S| <.0001
Quantiles (Definition 5)
Quantile Estimate
100% Max 0.19040469
99% 0.10076897
95% 0.04995763
90% 0.03947617
75% Q3 0.02102730
50% Median 0.01560388
25% Q1 0.01238808
10% 0.01075212
5% 0.01037395
1% 0.00993415
0% Min 0.00993415
The UNIVARIATE Procedure
Variable: lev (Leverage)
Extreme Observations
-------Lowest------- ------Highest------
Value Obs Value Obs
0.00993415 160 0.0799200 29
0.00993415 90 0.0846260 115
0.00993415 12 0.0855655 54
0.01008300 151 0.1007690 64
0.01009729 108 0.1904047 21
Missing Values
-----Percent Of-----
Missing Missing
Value Count All Obs Obs
. 17 8.50 100.00
Section 11.3
Page 274, middle of page. Make studentized residual and show largest value.
proc reg data=davisIn;
model reptwt = measwt female measwt_f;
output out=dvsRs rstudent=rs; /*studentized residuals*/
run;
quit;
proc univariate data=dvsRs;
var rs;
run;
proc print data=dvsRs;
where rs < -24.3 AND rs ne .;
run;
The REG Procedure
Model: MODEL1
Dependent Variable: reptwt
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 30655 10218 470.41 <.0001
Error 179 3888.25423 21.72209
Corrected Total 182 34543
Root MSE 4.66070 R-Square 0.8874
Dependent Mean 65.62295 Adj R-Sq 0.8856
Coeff Var 7.10224
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 1.35864 3.27719 0.41 0.6789
measwt 1 0.98982 0.04260 23.24 <.0001
female 1 39.96412 3.92932 10.17 <.0001
measwt_f 1 -0.72536 0.05598 -12.96 <.0001
The UNIVARIATE Procedure
Variable: rs (Studentized Residual without Current Obs)
Moments
N 183 Sum Weights 183
Mean -0.0961781 Sum Observations -17.60059
Std Deviation 2.00831794 Variance 4.03334093
Skewness -9.637042 Kurtosis 117.053571
Uncorrected SS 735.76084 Corrected SS 734.068049
Coeff Variation -2088.1242 Std Error Mean 0.14845913
Basic Statistical Measures
Location Variability
Mean -0.09618 Std Deviation 2.00832
Median -0.02849 Variance 4.03334
Mode -0.18673 Range 27.80109
Interquartile Range 0.95002
Tests for Location: Mu0=0
Test -Statistic- -----p Value------
Student's t t -0.64784 Pr > |t| 0.5179
Sign M -2.5 Pr >= |M| 0.7676
Signed Rank S -188 Pr >= |S| 0.7941
Quantiles (Definition 5)
Quantile Estimate
100% Max 3.4966276
99% 3.0813780
95% 1.5666415
90% 1.0406940
75% Q3 0.4462518
50% Median -0.0284926
25% Q1 -0.5037653
10% -0.9816218
5% -1.4664439
1% -2.3493765
0% Min -24.3044630
The UNIVARIATE Procedure
Variable: rs (Studentized Residual without Current Obs)
Extreme Observations
------Lowest------ -----Highest-----
Value Obs Value Obs
-24.30446 12 1.89365 129
-2.34938 29 2.39320 31
-2.18985 155 2.90657 64
-1.95943 130 3.08138 50
-1.90865 153 3.49663 115
Missing Values
-----Percent Of-----
Missing Missing
Value Count All Obs Obs
. 17 8.50 100.00
Obs subject sex measwt measht reptwt reptht measwt_f female rs
12 12 F 166 57 56 163 166 1 -24.3045
Section 11.4
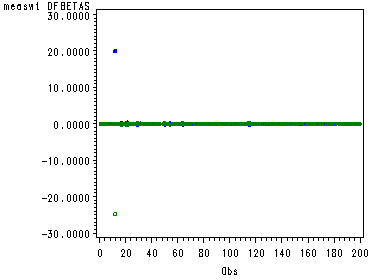
Middle of page 276, computing DFBETA for measwt, female and measwt_f. In our regression procedure, we use the option influence and use the ODS facilities to output a dataset that contains all the DFBETAS. The index plot shows an observation influencing female and influencing female*measwt.
proc reg data=davisIn;
model reptwt=measwt female measwt_f/influence ;
ods output OutputStatistics=dvsOut;
run;
quit;
filename outfiles 'https://stats.idre.ucla.edu/wp-content/uploads/2016/02/chp11dfbeta.gif';
goptions gsfname=outfiles dev=gif373;
symbol1 c=black i=none v=star h=0.5;
symbol2 c=blue i=none v=dot h=0.5;
symbol3 c=green i=none v=circle h=0.5;
proc gplot data=dvsOut;
plot (DFB_measwt)*observation=1
(DFB_female)*observation=2
(DFB_measwt_f)*observation=3/overlay;
run;
quit;
The REG Procedure
Model: MODEL1
Dependent Variable: reptwt
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 30655 10218 470.41 <.0001
Error 179 3888.25423 21.72209
Corrected Total 182 34543
Root MSE 4.66070 R-Square 0.8874
Dependent Mean 65.62295 Adj R-Sq 0.8856
Coeff Var 7.10224
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 1.35864 3.27719 0.41 0.6789
measwt 1 0.98982 0.04260 23.24 <.0001
female 1 39.96412 3.92932 10.17 <.0001
measwt_f 1 -0.72536 0.05598 -12.96 <.0001
The REG Procedure
Model: MODEL1
Dependent Variable: reptwt
Output Statistics
Hat Diag Cov ---------------DFBETAS--------------
Obs Residual RStudent H Ratio DFFITS Intercept measwt female measwt_f
1 -0.5749 -0.1238 0.0123 1.0350 -0.0138 -0.0010 -0.0012 0.0008 0.0009
2 -5.6614 -1.2225 0.0099 0.9989 -0.1223 -0.0000 0.0000 -0.0160 0.0019
3 -1.3391 -0.2883 0.0116 1.0327 -0.0312 -0.0000 0.0000 -0.0099 0.0078
: : : : : : : : : :
196 -3.6055 -0.7776 0.0125 1.0217 -0.0876 -0.0275 0.0141 0.0230 -0.0108
197 -3.5139 -0.7593 0.0163 1.0263 -0.0978 0.0353 -0.0492 -0.0294 0.0374
198 . . 0.0143 . . . . . .
199 0.5574 0.1210 0.0286 1.0525 0.0208 -0.0134 0.0157 0.0112 -0.0120
200 1.4454 0.3114 0.0130 1.0338 0.0357 -0.0031 0.0087 0.0026 -0.0066
Sum of Residuals 0
Sum of Squared Residuals 3888.25423
Predicted Residual SS (PRESS) 13623
The following segment illustrates the facility of SAS INSIGHT for scatterplot matrix from the command line. To some people it may be easier to do it from the SAS pulldown menus (e.g., click on Solutions then Analysis then Interactive Data Analysis).
proc insight data=dvsOut;
scatter DFB_measwt DFB_female DFB_measwt_f observation*
DFB_measwt DFB_female DFB_measwt_f observation;
run;
quit;
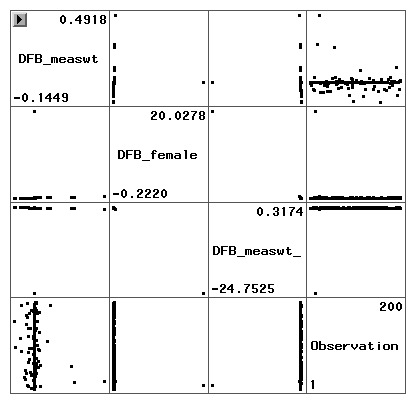
Bottom part of page 277, computing and showing Cook's D, DFFITS, DFBETAS.
Compute Cook's D and FFITS:
proc reg data=davisIn;
model reptwt=measwt female measwt_f;
output out=dvsSum cookd=ck;
run;
quit;
proc univariate data=dvsSum;
var ck;
run;
proc univariate data=dvsOut;
var dffits DFB_measwt DFB_female DFB_measwt_f;
run;
proc print data=dvsSum;
where subject=12;
var ck;
run;
proc print data=dvsOut;
where observation=12;
var dffits DFB_measwt DFB_female DFB_measwt_f;
quit;
The REG Procedure
Model: MODEL1
Dependent Variable: reptwt
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 30655 10218 470.41 <.0001
Error 179 3888.25423 21.72209
Corrected Total 182 34543
Root MSE 4.66070 R-Square 0.8874
Dependent Mean 65.62295 Adj R-Sq 0.8856
Coeff Var 7.10224
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 1.35864 3.27719 0.41 0.6789
measwt 1 0.98982 0.04260 23.24 <.0001
female 1 39.96412 3.92932 10.17 <.0001
measwt_f 1 -0.72536 0.05598 -12.96 <.0001
The UNIVARIATE Procedure
Variable: ck (Cook's D Influence Statistic)
Moments
N 183 Sum Weights 183
Mean 0.47387729 Sum Observations 86.7195445
Std Deviation 6.35162098 Variance 40.343089
Skewness 13.5276811 Kurtosis 182.998763
Uncorrected SS 7383.53663 Corrected SS 7342.44221
Coeff Variation 1340.35141 Std Error Mean 0.46952533
Basic Statistical Measures
Location Variability
Mean 0.473877 Std Deviation 6.35162
Median 0.000796 Variance 40.34309
Mode 0.000094 Range 85.92734
Interquartile Range 0.00309
Tests for Location: Mu0=0
Test -Statistic- -----p Value------
Student's t t 1.009269 Pr > |t| 0.3142
Sign M 91.5 Pr >= |M| <.0001
Signed Rank S 8418 Pr >= |S| <.0001
Quantiles (Definition 5)
Quantile Estimate
100% Max 8.59273E+01
99% 8.56294E-02
95% 1.99879E-02
90% 9.60576E-03
75% Q3 3.21741E-03
50% Median 7.96056E-04
25% Q1 1.24424E-04
10% 2.60263E-05
5% 2.28352E-05
1% 2.10827E-06
0% Min 2.10827E-06
The UNIVARIATE Procedure
Variable: ck (Cook's D Influence Statistic)
Extreme Observations
--------Lowest------- -------Highest------
Value Obs Value Obs
2.10827E-06 186 0.0624604 50
2.10827E-06 92 0.0651360 21
2.10827E-06 85 0.0701759 64
1.57302E-05 143 0.0856294 115
1.85113E-05 160 85.9273459 12
Missing Values
-----Percent Of-----
Missing Missing
Value Count All Obs Obs
. 17 8.50 100.00
The UNIVARIATE Procedure
Variable: DFFITS
Moments
N 183 Sum Weights 183
Mean -0.2012365 Sum Observations -36.826272
Std Deviation 2.84379473 Variance 8.08716846
Skewness -13.482793 Kurtosis 182.187495
Uncorrected SS 1479.27545 Corrected SS 1471.86466
Coeff Variation -1413.1608 Std Error Mean 0.21021936
Basic Statistical Measures
Location Variability
Mean -0.20124 Std Deviation 2.84379
Median -0.00290 Variance 8.08717
Mode -0.01930 Range 39.02263
Interquartile Range 0.11521
Tests for Location: Mu0=0
Test -Statistic- -----p Value------
Student's t t -0.95727 Pr > |t| 0.3397
Sign M -2.5 Pr >= |M| 0.7676
Signed Rank S -149 Pr >= |S| 0.8362
Quantiles (Definition 5)
Quantile Estimate
100% Max 0.60332360
99% 0.54072498
95% 0.21210692
90% 0.13627407
75% Q3 0.05600517
50% Median -0.00289586
25% Q1 -0.05920213
10% -0.11742211
5% -0.19584990
1% -0.43084786
0% Min -38.41931120
UNIVARIATE Procedure
Variable: DFFITS
Extreme Observations
-------Lowest------ ------Highest-----
Value Obs Value Obs
-38.419311 12 0.351835 17
-0.430848 29 0.510867 21
-0.296132 130 0.511565 50
-0.282346 155 0.540725 64
-0.260521 128 0.603324 115
Missing Values
-----Percent Of-----
Missing Missing
Value Count All Obs Obs
. 17 8.50 100.00
The UNIVARIATE Procedure
Variable: DFB_measwt (measwt DFBETAS)
Moments
N 183 Sum Weights 183
Mean 0.00039965 Sum Observations 0.07313633
Std Deviation 0.05401908 Variance 0.00291806
Skewness 5.26547487 Kurtosis 43.7449484
Uncorrected SS 0.53111634 Corrected SS 0.53108711
Coeff Variation 13516.5265 Std Error Mean 0.00399321
Basic Statistical Measures
Location Variability
Mean 0.000400 Std Deviation 0.05402
Median 0.000000 Variance 0.00292
Mode 0.000000 Range 0.63678
Interquartile Range 0.0000766
Tests for Location: Mu0=0
Test -Statistic- -----p Value------
Student's t t 0.100083 Pr > |t| 0.9204
Sign M 19.5 Pr >= |M| 0.0048
Signed Rank S 715 Pr >= |S| 0.3204
Quantiles (Definition 5)
Quantile Estimate
100% Max 4.91842E-01
99% 2.80931E-01
95% 3.14289E-02
90% 1.41305E-02
75% Q3 6.86667E-16
50% Median 3.14532E-17
25% Q1 -7.65658E-05
10% -4.27876E-02
5% -5.94060E-02
1% -1.31842E-01
0% Min -1.44941E-01
The UNIVARIATE Procedure
Variable: DFB_measwt (measwt DFBETAS)
Extreme Observations
-------Lowest------ ------Highest------
Value Obs Value Obs
-0.1449406 156 0.0881442 111
-0.1318417 97 0.1096412 191
-0.0978029 118 0.2565254 54
-0.0921938 87 0.2809306 17
-0.0904702 192 0.4918421 21
Missing Values
-----Percent Of-----
Missing Missing
Value Count All Obs Obs
. 17 8.50 100.00
The UNIVARIATE Procedure
Variable: DFB_female (female DFBETAS)
Moments
N 183 Sum Weights 183
Mean 0.09419919 Sum Observations 17.2384525
Std Deviation 1.48275408 Variance 2.19855965
Skewness 13.4966624 Kurtosis 182.435032
Uncorrected SS 401.761705 Corrected SS 400.137857
Coeff Variation 1574.06238 Std Error Mean 0.10960834
Basic Statistical Measures
Location Variability
Mean 0.09420 Std Deviation 1.48275
Median -0.00501 Variance 2.19856
Mode -0.00481 Range 20.24974
Interquartile Range 0.03337
Tests for Location: Mu0=0
Test -Statistic- -----p Value------
Student's t t 0.859416 Pr > |t| 0.3912
Sign M -32.5 Pr >= |M| <.0001
Signed Rank S -3776 Pr >= |S| <.0001
Quantiles (Definition 5)
Quantile Estimate
100% Max 20.02775272
99% 0.38703149
95% 0.03421111
90% 0.01663061
75% Q3 0.00396153
50% Median -0.00500628
25% Q1 -0.02941105
10% -0.06352601
5% -0.11406227
1% -0.22172649
0% Min -0.22199219
The UNIVARIATE Procedure
Variable: DFB_female (female DFBETAS)
Extreme Observations
------Lowest------ -------Highest------
Value Obs Value Obs
-0.221992 115 0.0758795 191
-0.221726 29 0.1956965 54
-0.209797 64 0.2036534 17
-0.182301 50 0.3870315 21
-0.142343 130 20.0277527 12
Missing Values
-----Percent Of-----
Missing Missing
Value Count All Obs Obs
. 17 8.50 100.00
The UNIVARIATE Procedure
Variable: DFB_measwt_f (measwt_f DFBETAS)
Moments
N 183 Sum Weights 183
Mean -0.1163372 Sum Observations -21.28971
Std Deviation 1.83226898 Variance 3.35720963
Skewness -13.503022 Kurtosis 182.551683
Uncorrected SS 613.488939 Corrected SS 611.012153
Coeff Variation -1574.9638 Std Error Mean 0.13544522
Basic Statistical Measures
Location Variability
Mean -0.11634 Std Deviation 1.83227
Median 0.00546 Variance 3.35721
Mode 0.00314 Range 25.06990
Interquartile Range 0.03505
Tests for Location: Mu0=0
Test -Statistic- -----p Value------
Student's t t -0.85892 Pr > |t| 0.3915
Sign M 40.5 Pr >= |M| <.0001
Signed Rank S 4418 Pr >= |S| <.0001
Quantiles (Definition 5)
Quantile Estimate
100% Max 0.31740249
99% 0.29435380
95% 0.11029567
90% 0.07015686
75% Q3 0.03286291
50% Median 0.00546108
25% Q1 -0.00218745
10% -0.01330578
5% -0.02563021
1% -0.37427787
0% Min -24.75250165
The UNIVARIATE Procedure
Variable: DFB_measwt_f (measwt_f DFBETAS)
Extreme Observations
-------Lowest------- ------Highest-----
Value Obs Value Obs
-24.7525017 12 0.155113 31
-0.3742779 21 0.233150 29
-0.2137802 17 0.263616 50
-0.1952085 54 0.294354 64
-0.0834338 191 0.317402 115
Missing Values
-----Percent Of-----
Missing Missing
Value Count All Obs Obs
. 17 8.50 100.00
Obs ck(Cook's D)
12 85.9273
DFB_ DFB_ DFB_
Obs DFFITS measwt female measwt_f
12 -38.4193 -0.0000 20.0278 -24.7525
Top of page 279, computing COVRATIO. Dataset dvsOut already contains it. We summarize it with proc univariate.
proc univariate data=dvsOut;
var covratio;
run;
proc print data=dvsOut;
where covratio<0.02 and covratio ge 0;
run;
quit;
The UNIVARIATE Procedure
Variable: CovRatio (Cov Ratio)
Moments
N 183 Sum Weights 183
Mean 1.01845274 Sum Observations 186.376851
Std Deviation 0.08330185 Variance 0.0069392
Skewness -9.9649448 Kurtosis 119.302488
Uncorrected SS 191.078948 Corrected SS 1.26293396
Coeff Variation 8.17925499 Std Error Mean 0.00615785
Basic Statistical Measures
Location Variability
Mean 1.018453 Std Deviation 0.08330
Median 1.030849 Variance 0.00694
Mode 1.032772 Range 1.18186
Interquartile Range 0.01719
Tests for Location: Mu0=0
Test -Statistic- -----p Value------
Student's t t 165.391 Pr > |t| <.0001
Sign M 91.5 Pr >= |M| <.0001
Signed Rank S 8418 Pr >= |S| <.0001
Quantiles (Definition 5)
Quantile Estimate
100% Max 1.1921500
99% 1.0969195
95% 1.0674884
90% 1.0458427
75% Q3 1.0370553
50% Median 1.0308486
25% Q1 1.0198622
10% 0.9867116
5% 0.9600152
1% 0.8073648
0% Min 0.0102869
The UNIVARIATE Procedure
Variable: CovRatio (Cov Ratio)
Extreme Observations
-------Lowest------ -----Highest-----
Value Obs Value Obs
0.0102869 12 1.07503 65
0.8073648 115 1.07525 82
0.8536158 50 1.09106 30
0.8789338 64 1.09692 97
0.9190747 31 1.19215 21
Missing Values
-----Percent Of-----
Missing Missing
Value Count All Obs Obs
. 17 8.50 100.00
Hat
Obs Residual RStudent Diagonal
12 -29.2230 -24.3045 0.7142
Obs CovRatio DFFITS
12 0.0103 -38.4193
Section 11.6
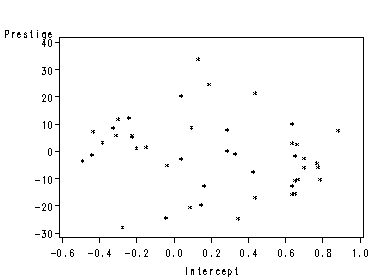
Page 283 bottom, and figure 11.5 page 284, partial regression plots using data file duncan. We construct a partial regression plot for intercept based on the second footnote on page 283.
data duncan1; /* to create a constant regressor */ set duncan; Int=1; proc reg data=duncan1 noprint; model prestige Int= income educ / noint; /* the option of no intercept*/ output out=temp r=ry rx; run; filename outfiles 'https://stats.idre.ucla.edu/wp-content/uploads/2016/02/chp11pInt.gif'; goptions gsfname=outfiles dev=gif373; proc gplot data=temp; plot ry*rx /hminor=0 vminor=0; label ry='Prestige' rx='Intercept'; run;
Following program produces Figure 11.5.on page 284.
filename outfiles 'https://stats.idre.ucla.edu/wp-content/uploads/2016/02/chp11pInc.gif'; goptions gsfname=outfiles dev=gif373; proc reg data=duncan; model prestige income=educ; output out=dnEd r=prst inc; run; proc reg data=dnEd; model prst=inc; plot prst*inc /haxis=(-50 to 75 by 25) vaxis=(-50 to 100 by 50) nomodel nostat; label prst='Prestige'; label inc='Income'; run; quit; filename outfiles 'https://stats.idre.ucla.edu/wp-content/uploads/2016/02/chp11ped.gif'; goptions gsfname=outfiles dev=gif373; proc reg data=duncan; model prestige educ=income; output out=dcInc r=prst ed; run; proc reg data=dcInc; model prst=ed; plot prst*ed / haxis=(-75 to 50 by 25) vaxis=(-50 to 100 by 50) nomodel nostat; label prst='Prestige'; label ed='Education'; run; quit;
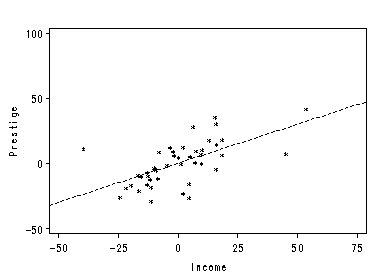
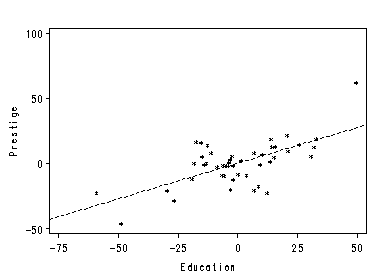
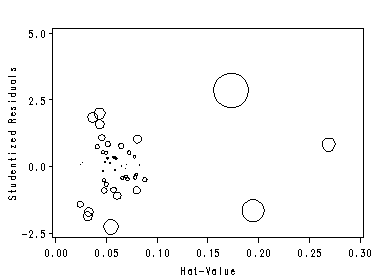
Figure 11.6. Bubble plot.
filename outfiles 'https://stats.idre.ucla.edu/wp-content/uploads/2016/02/chp11bbl.gif'; goptions gsfname=outfiles dev=gif373; proc reg data=duncan; model prestige=income educ; output out=dncnOut cookd=ck h=lev student=rs; run; quit; axis1 order=(0 to 0.3 by 0.05); axis2 order=(-2.5 to 5 by 2.5) label=(r=0 a=90); proc gplot data=dncnOut; bubble rs*lev=ck /haxis=axis1 vaxis=axis2 bsize=10 hminor=0 vminor=0; label rs='Studentized Residuals'; label lev='Hat-Value'; run; quit;