Section 12.1 Nonnormally Distributed Errors
Figure 12.1 (a) and (b) on page 297 and using data file ornstein.
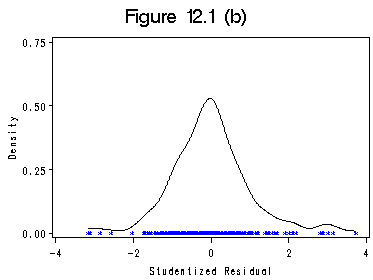
data ornstein_co; /*Dummy coding: baseline is 'CAN' for nation and 'MAN' for sector*/ set ornstein; asset1 = sqrt(assets); inlcks = sqrt(intrlcks+1); Array n(3); do i =1 to 3; n(i)=0; end; Array sec(9); do i = 1 to 9; sec(i)=0; end; drop i; if (nation='OTH') then n1=1; if (nation='UK') then n2=1; if (nation='US') then n3=1; if (sector='BNK') then sec1=1; if (sector='CON') then sec2=1; if (sector='FIN') then sec3=1; if (sector='HLD') then sec4=1; if (sector='AGR') then sec5=1; if (sector='MER') then sec6=1; if (sector='MIN') then sec7=1; if (sector='TRN') then sec8=1; if (sector='WOD') then sec9=1; run; proc reg data=ornstein_co;/*model for the first graph*/ model intrlcks = asset1 sec1-sec9 n1-n3; output out=rstq1 rstudent=rstd p=prd; run; quit; symbol1 c=black v=star h=0.5; title 'Figure 12.1 (a)'; proc univariate data=rstq1;/*Figure 12.1*/ var rstd; qqplot /normal (mu=est sigma=est color=blue w=1.5 ); label rstd='Studentized Residual'; run;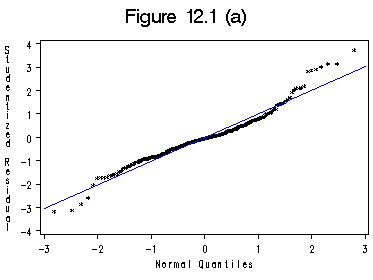
proc kde data=rstq1 out=kdeorn; /*create density distribution*/ var rstd; run; data kdeorn1; set kdeorn; if count ne 0 then mycount=0.00001;/*dummy for one-way plot*/ output; run; proc sort data=kdeorn1; by rstd; run; title 'Figure 12.1 (b)'; symbol1 c=black i=join v=none h=0.8; symbol2 c= blue i =none v=star h=0.5; axis1 order= (-4 to 4 by 2); axis2 order =(0 to 0.75 by 0.25) label=(r=0 a=90); proc gplot data=kdeorn1 ; plot density*rstd=1 mycount*rstd=2/overlay haxis=axis1 vaxis=axis2 hminor=0 vminor=0; label density='Density'; label rstd='Studentized Residual'; run; quit;
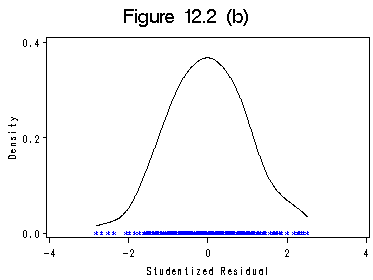
proc reg data=ornstein_co;/*second model*/ model inlcks= asset1 sec1-sec9 n1-n3; output out=rstq2 rstudent=rstd p=prd; run; quit; symbol1 c=black v=star h=0.5; title 'Figure 12.2 (a)'; proc univariate data=rstq2;/*Figure 12.1 (a)*/ var rstd; qqplot /normal (mu=est sigma=est color=blue w=1.5 ); label rstd='Studentized Residual'; run;proc kde data=rstq2 out=kdeorn2; /*create density distribution*/ var rstd; run; quit; data kdeorn3; set kdeorn2; if count ne 0 then mycount=0.00001; output; run; proc sort data=kdeorn3; by rstd; run; title 'Figure 12.2 (b)'; symbol1 c=black i=join v=none l=0.2; symbol2 c= blue i =none h=0.5;; axis1 order= (-4 to 4 by 2); axis2 order =(0 to 0.4 by 0.2) label=(r=0 a=90); proc gplot data=kdeorn3; plot density*rstd=1 mycount*rstd=2/overlay haxis=axis1 vaxis=axis2 hminor=0 vminor=0; label density='Density'; label rstd='Studentized Residual'; run; quit;
Table 12.1 can be obtained from the regression run above.
The REG Procedure
Model: MODEL1
Dependent Variable: intrlcks
(Omit Analysis of Variance)
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 4.19045 1.84604 2.27 0.0241
asset1 1 0.25179 0.01852 13.59 <.0001
sec1 1 -14.37594 5.57699 -2.58 0.0106
sec2 1 -5.12563 4.69878 -1.09 0.2765
sec3 1 -5.69851 2.92571 -1.95 0.0526
sec4 1 -2.43024 4.01411 -0.61 0.5455
sec5 1 -1.19954 2.04038 -0.59 0.5572
sec6 1 -0.86685 2.63433 -0.33 0.7424
sec7 1 0.34228 2.01210 0.17 0.8651
sec8 1 -0.38104 2.81974 -0.14 0.8926
sec9 1 5.15130 2.68208 1.92 0.0560
n1 1 -1.15891 2.66400 -0.44 0.6639
n2 1 -4.44401 2.64928 -1.68 0.0948
n3 1 -8.08905 1.48100 -5.46 <.0001
The REG Procedure
Model: MODEL1
Dependent Variable: inlcks
(Omit Analysis of Variance)
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 2.32931 0.23087 10.09 <.0001
asset1 1 0.02601 0.00232 11.23 <.0001
sec1 1 -2.25076 0.69749 -3.23 0.0014
sec2 1 -0.73997 0.58765 -1.26 0.2092
sec3 1 -0.08804 0.36590 -0.24 0.8101
sec4 1 -0.24532 0.50202 -0.49 0.6255
sec5 1 -0.05672 0.25518 -0.22 0.8243
sec6 1 0.14791 0.32946 0.45 0.6539
sec7 1 0.35620 0.25164 1.42 0.1582
sec8 1 0.35401 0.35265 1.00 0.3165
sec9 1 0.78604 0.33543 2.34 0.0200
n1 1 -0.11396 0.33317 -0.34 0.7326
n2 1 -0.52660 0.33133 -1.59 0.1133
n3 1 -1.10511 0.18522 -5.97 <.0001
Section 12.2 Nonconstant Error Variance
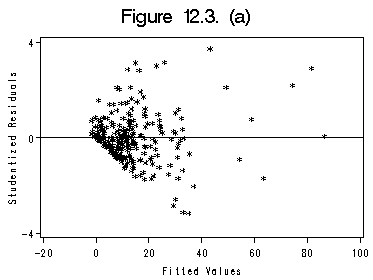
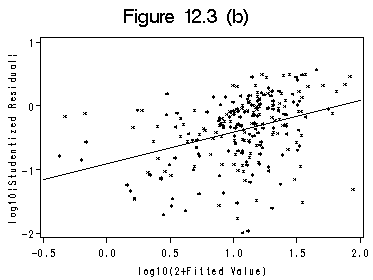
Continuation on data file ornstein from previous section. Figure 12.3 (a) and (b) on page 303.
data fitted; set rstq1; newfit= log10(2+prd); rstlog=log10(abs(rstd)); run; symbol c=black i=none v=star h=0.8; axis1 order=(-20 to 100 by 20); axis2 order=(-4 to 4 by 4)label=(r=0 a=90); title 'Figure 12.3. (a)'; proc gplot data=rstq1; plot rstd*prd /haxis=axis1 vaxis=axis2 vminor=0 hminor=0 vref=0 ; label prd='Fitted Values'; label rstd='Studentized Residuals'; run; quit;
title 'Figure 12.3 (b)'; symbol interpol=r value = star h=0.4 cv=black width=1; axis1 order =(-0.5 to 2 by .5); axis2 order =(-2 to 1 by 1) label=(r=0 a=90); proc gplot data=fitted; plot rstlog*newfit /haxis=axis1 vaxis=axis2 hminor=0 vminor=0; label newfit='log10(2+Fitted Value)'; label rstlog='log10|Studentized Residual|'; run; quit;
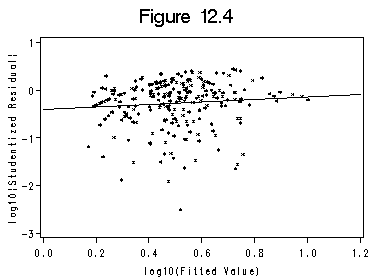
data fitted1; set rstq2; logfit=log10(prd); logr=log10(abs(rstd)); run; title 'Figure 12.4'; symbol interpol=r value = star h=0.4 cv=black width=1; axis1 order =(0 to 1.2 by .2); axis2 order =(-3 to 1 by 1) label=(r=0 a=90); proc gplot data=fitted1; plot logr*logfit /vminor=0 hminor=0 haxis=axis1 vaxis=axis2; label logfit='log10(Fitted Value)'; label logr='log10|Studentized Residual|'; run; quit;
Section 12.3 Nonlinearity
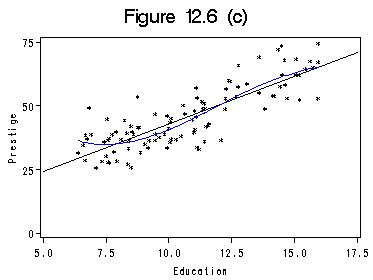
Figure 12.6 using data file prestige. Option partial in proc reg produces the partial residual plots in line-printer format. Here we show the steps to produce high-resolution partial residual plots.
proc reg data=prestige; model prestige=educat income percwomn; output out=partial r=r; run; quit; data mypar; set partial; redu = r+4.18664*educat; /*coefficient from previous procedure*/ rinc = r+0.00131*income; /*coefficient from previous procedure*/ rper = r-0.00891*percwomn; /*coefficient from previous procedure*/ Obs=_n_; run; proc loess data=mypar;/*get the smoothing curve*/ model redu=educat/smooth=0.5; ods output OutputStatistics=stat1; run; quit; data comedu; merge stat1 mypar ; by Obs; run; proc sort data=comedu; by educat; run; title 'Figure 12.6 (a)'; axis1 order =(5 to 17.5 by 2.5); axis2 order =(0 to 100 by 25) label=(r=0 a=90); symbol1 color=black i=r v=star h=0.5; symbol2 color=blue i=join v=none; proc gplot data=comedu; format educat 4.1; plot redu*educat=1 Pred*educat=2/ haxis=axis1 vaxis=axis2 vminor=0 hminor=0 overlay; label educat='Eucation'; label redu='Partial Residual'; run; quit;proc loess data=mypar; model rinc = income /smooth=0.5; ods output OutputStatistics=stat2; run; quit; data cominc; merge stat2 mypar ; by Obs; run; proc sort data=cominc; by income; run; title 'Figure 12.6 (b)'; axis1 order=(0 to 30000 by 10000); axis2 order=(-25 to 50 by 25) label=(r=0 a=90); proc gplot data=cominc; format rinc 4.1; format Pred 4.1; plot rinc*income =1 Pred*income=2 / overlay haxis=axis1 vaxis=axis2 vminor=0 hminor=0; label income='Income'; label rinc='Partial Residual'; run; quit;
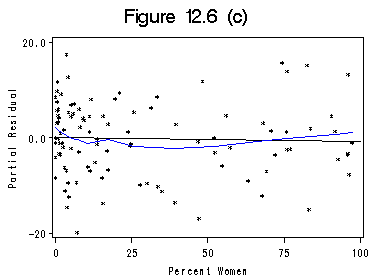
proc loess data=mypar; model rper = percwomn /smooth=0.5; ods output OutputStatistics=stat3; run; quit; data comper; merge stat3 mypar ; by Obs; run; proc sort data=comper; by percwomn; run; title 'Figure 12.6 (c)'; axis1 order =(0 to 100 by 25); axis2 order =(-20 to 20 by 20) label=(r=0 a=90); proc gplot data=comper; format rper 4.1 Pred 4.1 percwomn 4.0; plot rper*percwomn=1 Pred*percwomn=2/ overlay haxis=axis1 vaxis=axis2 vminor=0 hminor=0; label percwomn='Percent Women'; label rper='Partial Residual'; run; quit;
Calculation on page 303 and Figure 12.7 on page 304.
data prestige1;
set prestige;
inc2 = log2(income);
edu2 = educat*educat;
edu3 = edu2*educat;
percwomn2=percwomn*percwomn;
run;
proc reg data=prestige1;/*Formula in the middle of page 313.*/
model prestige = inc2 educat edu2 edu3 percwomn percwomn2;
output out=prst_par r=r;
run;
quit;
data manually;
set prst_par;
prd=20.8 + 8.78*log2(6798)-0.179*29+0.0025*29*29-29.9*educat+2.91*edu2-0.0808*edu3;
par = r+prd;
run;
proc sort data=manually;
by educat;
run;
axis1 order=(5 to 17.5 by 2.5);
axis2 order =(0 to 75 by 25)label =(r=0 a=90);
proc gplot data=manually;
plot par*educat=1 prd*educat=2/overlay haxis=axis1 vaxis=axis2 vminor=0 hminor=0;
label educat='Education';
label par='Prestige';
run;
quit;
The REG Procedure
Model: MODEL1
Dependent Variable: prestige
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 6 25604 4267.27481 94.46 <.0001
Error 95 4291.77780 45.17661
Corrected Total 101 29895
Root MSE 6.72135 R-Square 0.8564
Dependent Mean 46.83333 Adj R-Sq 0.8474
Coeff Var 14.35165
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 20.83821 56.89953 0.37 0.7150
inc2 1 8.78333 1.27275 6.90 <.0001
educat 1 -29.91994 15.25151 -1.96 0.0527
edu2 1 2.91593 1.41441 2.06 0.0420
edu3 1 -0.08068 0.04221 -1.91 0.0590
percwomn 1 -0.17932 0.08509 -2.11 0.0377
percwomn2 1 0.00250 0.00092446 2.70 0.0081
Section 12.4 Discrete Data
Table 12.2 on page 319 using data file vocab.
proc reg data=vocab;/*linear effect*/
model vocab = educ;
run;
quit;
data vocadm;/*create dummy variables*/
set vocab;
Array d(19);
do i = 1 to 19;
d(i)=0;
end;
drop i;
if educ=1 then d1=1;
else if educ ge 3 then d(educ-1)= 1;
run;
proc reg data=vocadm;/*test on nonlinear effect*/
model vocab = d1-d18 educ;
test d1, d2, d3, d4, d5, d6, d7, d8, d9, d10, d11, d12, d13, d14, d15, d16, d17, d18;
run;
quit;
The REG Procedure
Model: MODEL1
Dependent Variable: vocab
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 1175.11129 1175.11129 318.92 <.0001
Error 966 3559.41351 3.68469
Corrected Total 967 4734.52479
Root MSE 1.91956 R-Square 0.2482
Dependent Mean 5.94008 Adj R-Sq 0.2474
Coeff Var 32.31530
(rest of the output omitted.)
The REG Procedure
Model: MODEL1
Dependent Variable: vocab
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 19 1261.69388 66.40494 18.13 <.0001
Error 948 3472.83091 3.66332
Corrected Total 967 4734.52479
Root MSE 1.91398 R-Square 0.2665
Dependent Mean 5.94008 Adj R-Sq 0.2518
Coeff Var 32.22146
(rest of the output omitted.)
The REG Procedure
Model: MODEL1
Test 1 Results for Dependent Variable vocab
Mean
Source DF Square F Value Pr > F
Numerator 18 4.81014 1.31 0.1706
Denominator 948 3.66332
Section 12. 5 Maximum-Likelihood Methods
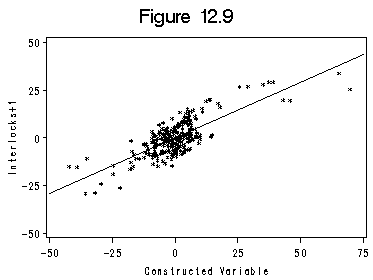
Box-Cox and Box-Tidwell transformation. Calculation on page 323 and Figure 12.9 on data file ornstein.
data ornstein1;/*coding dummy variables*/
set ornstein;
Array sec(9);
do i = 1 to 9;
sec(i)=0;
end;
Array nat(3);
do i =1 to 3;
nat(i)=0;
end;
drop i;
if nation = 'OTH' then nat(1)=1;/*baseline: Canada*/
if nation = 'UK' then nat(2)=1;
if nation = 'US' then nat(3)=1;
if sector = 'AGR' then sec1=1;/*baseline: Heavy manufacturing*/
if sector = 'BNK' then sec2=1;
if sector = 'CON' then sec3=1;
if sector = 'FIN' then sec4=1;
if sector = 'HLD' then sec5=1;
if sector = 'MER' then sec6=1;
if sector = 'MIN' then sec7=1;
if sector = 'TRN' then sec8=1;
if sector = 'WOD' then sec9=1;
output;
run;
data orn1;/*geometric mean*/
set ornstein1 ;
retain yg 0;
yg = yg + log(intrlcks+1);
size = _n_;
ygeo=exp(yg/size);
keep ygeo;
if _n_ = 248 then output;/*original dataset has 248 observations*/
run;
data orn2;
set ornstein1;
y1=intrlcks+1;
asset1=sqrt(assets);
g=y1*(log(y1/8.25013)-1);
run;
proc reg data=orn2;
model y1=sec1-sec9 nat1-nat3 asset1 g;
output out = orn2reg r=r;
run;
test g=0;
quit;
The REG Procedure
Model: MODEL1
Dependent Variable: y1
(omitted most of the output here.)
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 11.41614 1.21721 9.38 <.0001
(more variables in between)
g 1 0.58504 0.03132 18.68 <.0001
Remark: 1-g gives the estimated transformation. The t-test below assesses the
need for a transformation.
Test 1 Results for Dependent Variable y1
Mean
Source DF Square F Value Pr > F
Numerator 1 13232 348.86 <.0001
Denominator 233 37.92986
proc reg data=orn2reg noprint;/*partial regression*/ model y1=sec1-sec9 nat1-nat3 asset1; output out=orn3reg r=rg; run; quit; proc reg data=orn3reg noprint; model g=sec1-sec9 nat1-nat3 asset1; output out=orn4reg r=rg1; run; quit; axis1 order=(-50 to 75 by 25); axis2 order=(-50 to 50 by 25) label=(r=0 a=90); title 'Figure 12.9'; proc gplot data=orn4reg;/* Figure 12.9 */ plot rg*rg1 /haxis=axis1 vaxis=axis2 hminor=0 vminor=0; label rg1='Constructed Variable'; label rg='Interlocks+1'; run; quit;
The adxtrans and adxgen are SAS macro that produces MLE's of the dependent variable. The two '*' shown in the output in column adxconf says that the parameter should be between 0.2 and 0.4.
%adxgen %adxtrans(orn2, ornout, y1, assets sec1 sec2 sec3 sec4 sec5 sec6 sec7 sec8 sec9 nat1 nat2 nat3);
Obs adxlam _RMSE_ adxconf 1 -2.0 82.5764 2 -1.8 59.7584 3 -1.6 43.6997 4 -1.4 32.3614 5 -1.2 24.3342 6 -1.0 18.6427 7 -0.8 14.6118 8 -0.6 11.7750 9 -0.4 9.8116 10 -0.2 8.5037 11 0.0 7.7072 12 0.2 7.3333 * 13 0.4 7.3375 * 14 0.6 7.7164 15 0.8 8.5123 16 1.0 9.8265 17 1.2 11.8452 18 1.4 14.8828 19 1.6 19.4519 20 1.8 26.3746 21 2.0 36.9602
Likelihood for Power
Plot of _RMSE_*adxlam. Symbol used is 'L'.| | 100 + R | o | o | t | L 80 + m | e | a | n | 60 + L s | q | u | a | L r 40 + e | L d | L | L e | L r 20 + L L r | L L o | L L r | L L L L L L L L | 0 + | ---+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-- -2.0 -1.6 -1.2 -0.8 -0.4 0.0 0.4 0.8 1.2 1.6 2.0
adxlam
Section 12.5.2 on Box-Tidwell Transformation using data file prestige. SAS8 does not have a procedure that does the transformation yet. Michael Friendly in York University has written a macro boxtid that does it. Interested readers should consult his webpage for more details on this macro and its usage. We will only cover the constructed variable plots.
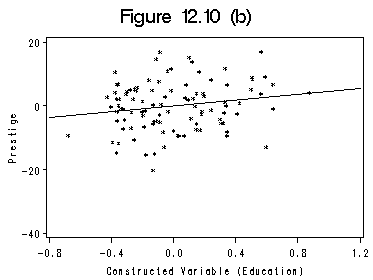
data prst1; set prestige; w2=percwomn**2; linc=income*log(income); ledu=educat*log(educat); run; proc reg data=prst1; model prestige=percwomn w2 educat income; output out=cvp r=res; run; quit; proc reg data=cvp noprint; model linc=percwomn w2 educat income; output out=cvp1 r=res1; run; quit; title 'Figure 12.10 (a)'; axis1 order=(-4000 to 8000 by 4000); axis2 order =(-40 to 20 by 20) label=(r=0 a=90); symbol1 c=black i=rl v=star; proc gplot data=cvp1; plot res*res1=1/haxis=axis1 vaxis=axis2 vminor=0 hminor=0; label res1='Constructed Variable (Income)'; label res='Prestige'; run; quit;proc reg data=cvp noprint; model ledu=percwomn w2 income educat; output out=cvp2 r=res2; run; quit; title 'Figure 12.10 (b)'; axis1 order=(-0.8 to 1.2 by .4); axis2 order =(-40 to 20 by 20) label=(r=0 a=90); symbol1 c=black i=rl v=star; proc gplot data=cvp2; plot res*res2=1/haxis=axis1 vaxis=axis2 vminor=0 hminor=0; label res2='Constructed Variable (Education)'; label res='Prestige'; run; quit;