Section 15.1 Models for Dichotomous Data
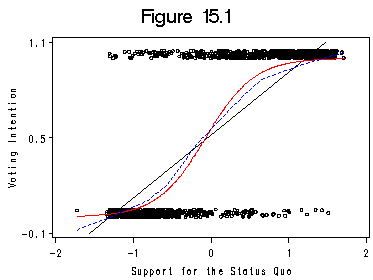
Figure 15.1. using data file chile.
data chilenew; /*jittered dataset*/
set chile;
if (intvote = 2) then voting = 0;
else voting = 1;
vjitter = voting + 0.05*ranuni(0);
if(intvote <3); /*1 for and 2 against*/
output;
run;
proc logistsic data=chilenew descending noprint; /*descending option is needed*/
model voting=statquo;
output out=chile1 predicted=lpred; /*output data file for further analysis*/
run;
proc loess data=chile1;
model voting=statquo;
ods output PredAtVertices=chile2;
run;
proc sort data=chile2;
by statquo;
proc sort data=chile1;
by statquo;
run;
data chile3;
merge chile1 chile2;
by statquo;
run;
goptions gsfname=outfiles dev=gif373;
symbol1 c=black i=rls v=circle h=0.5;
symbol2 c=red i=join v=none;
symbol3 c=blue i=join v=none h=0.5 line=2;
title 'Figure 15.1';
filename outfiles 'https://stats.idre.ucla.edu/wp-content/uploads/2016/02/chp15Fig1.gif';
axis1 order = (-2 to 2 by 1);
axis2 order = (-0.1 to 1.1 by 0.6) label=(r=0 a=90);;
proc gplot data=chile3;
format statquo f2.0;
plot vjitter*statquo=1 lpred*statquo=2 Pred*statquo=3 / haxis=axis1
vaxis=axis2 overlay vminor=0 hminor=0;
label statquo='Support for the Status Quo';
label vjitter='Voting Intention';
run;
quit;
Table 15.1 and Table 15.2 on page 452 using data file womenlf. In order to use proc logistic correctly, dummy variables are created to present the status of working, the presence of children and the region. The deviance in the table is -2*Log L which is presented in the output. The (G0)2 in Table 15.2 is the difference of -2*Log L between the two models being compared. The p-value is then obtained using chi-square distribution with the corresponding degree of freedom. On the other hand, proc logistic uses Wald-test (shown below) instead of (G0)2.
data wcoded; set womenlf; if (work='not_work') then wstatus=0; else wstatus =1; if (child ='present') then kid = 1; else kid =0; if (region ='Ontario') then re1= 1; else re1 =0; if (region ='Prairie') then re2=1; else re2=0; if (region ='Atlantic') then re3=1; else re3=0; if (region = 'Quebec') then re4=1; else re4=0; ik=husbinc*kid; run; proc logistic data=wcoded;/*model 1*/ model wstatus = husbinc kid re1-re4 ik; test2: test ik;/* model contrast:2-1*/ test5: test re1, re2, re3, re4;/*model contrast : 3-1*/ run; proc logistic data=wcoded; /*model 2*/ model wstatus = husbinc kid re1-re4; test3: test husbinc;/*model contrast: 5-2*/ test4: test kid; /*model contrast: 4-2 */ run; proc logistic data=wcoded; /*model 3*/ model wstatus = husbinc kid ik; run; proc logistic data=wcoded; /*model 4*/ model wstatus = husbinc re1-re4; run; proc logistic data=wcoded;/*model 5*/ model wstatus = kid re1-re4; run;
The LOGISTIC Procedure ---Model 1---
(Output omitted here.)
Model Fit Statistics For Model 1
Intercept
Intercept and
Criterion Only Covariates
AIC 358.151 332.542
SC 361.723 361.119
-2 Log L 356.151 316.542
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 39.6094 7 <.0001
Score 38.6566 7 <.0001
Wald 33.8338 7 <.0001
Linear Hypotheses Testing Results
Wald
Label Chi-Square DF Pr > ChiSq
TEST2 0.7547 1 0.3850 --comparing model 2 with model 1
TEST5 2.5477 4 0.6361 --comparing model 3 with model 1
The LOGISTIC Procedure ---Model 2---
(Output omitted here.)
Model Fit Statistics For Model 2
Intercept
Intercept and
Criterion Only Covariates
AIC 358.151 331.301
SC 361.723 356.306
-2 Log L 356.151 317.301
Linear Hypotheses Testing Results
Wald
Label Chi-Square DF Pr > ChiSq
TEST3 4.8567 1 0.0275 --comparing model 5 and model 2
TEST4 28.2452 1 <.0001 --comparing model 4 and model 2
The LOGISTIC Procedure ---Model 3---
(Output omitted here.)
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 358.151 327.124
SC 361.723 341.413
-2 Log L 356.151 319.124
The LOGISTIC Procedure ---Model 4---
(Output omitted here.)
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 358.151 359.849
SC 361.723 381.282
-2 Log L 356.151 347.849
The LOGISTIC Procedure ---Model 5---
(Output omitted here.)
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 358.151 334.427
SC 361.723 355.860
-2 Log L 356.151 322.427
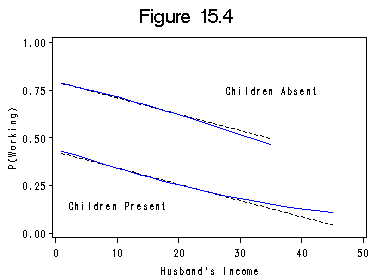
Figure 15.4 on page 453.
proc logistic data= wcoded descending noprint;
model wstatus = kid husbinc /rsquare;
output out=women predicted=pred;
run;
proc reg data=women noprint;
model wstatus = husbinc kid;
output out = women1 predicted=lpr;
run;
data women2; /*to create a dataset for gplot */
set women1;
if (kid=1) then do l1=lpr; p1=pred; end;
else do l2=lpr; p2=pred; end;
output;
run;
proc sort data=women2;
by husbinc;
run;
data labels; /*for the text in the graph*/
length function style $ 8 text $17;
retain function 'label' xsys ysys '2' when 'a' color 'black';
function='label'; x=10; y=0.15; size=1; color='black'; text='Children Present'; output;
function='label'; x=35; y=0.75; size=1; color='black'; text='Children Absent'; output;
run;
title 'Figure 15.4';
symbol1 c=black i=join v=none h=1 line=2;
symbol2 c=blue i=join v=none h=1 line=1;
axis1 order =(0 to 50 by 10);
axis2 order=(0 to 1 by .25) label=(r=0 a=90);
proc gplot data=women2;
plot l1*husbinc=1 l2*husbinc=1 p1*husbinc=2 p2*husbinc=2
/ annotate=labels haxis=axis1 vaxis=axis2 hminor=0 vminor=0 overlay;
label husbinc='Husband''s Income';
label l1='P(Working)';
run;
quit;
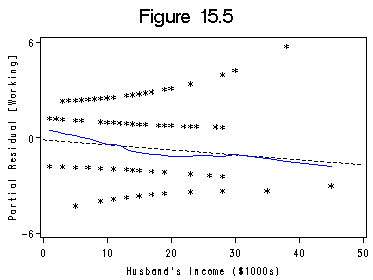
Figure 15.5 on page 459 using the same data file womenlf as above.
data wcoded1; set womenlf; if (work='not_work') then do w=2; wstatus=1; end; else if (work='fulltime') then do w=0; wstatus=0; end; else do w=1; wstatus =0; end; if (child ='present') then kid = 1; else kid =0; if (region ='Ontario') then re1= 1; else re1 =0; if (region ='Prairie') then re2=1; else re2=0; if (region ='Atlantic') then re3=1; else re3=0; if (region = 'Quebec') then re4=1; else re4=0; ik=husbinc*kid; run; proc logistic data=wcoded1 descending noprint; model wstatus =husbinc kid ; output out=women predicted=pr; run; data women1; /*to create partial residuals*/ set women; rh = (pr-wstatus)/(pr*(1-pr)) -0.0423*husbinc; run; proc loess data=women1;/*to create data for lowess smooth of the plot*/ model rh=husbinc /iterations=2 direct smooth=0.5; /*set iterations to be 2 for outliers*/ ods output OutputStatistics=women2; run; proc sort data=women1; by husbinc; run; proc sort data=women2; by husbinc; run; data women3; merge women1 women2; by husbinc; run; title 'Figure 15.5'; symbol1 color=black i=rls v=star h=0.8 line=2; symbol2 color=blue i=jone v=none h=1 line =1; axis1 order=(0 to 50 by 10); axis2 order=(-6 to 6 by 6) label=(r=0 a=90); proc gplot data=women3; format husbinc f4.0; plot rh*husbinc=1 Pred*husbinc=2/ overlay haxis=axis1 vaxis=axis2 vminor=0 hminor=0; label husbinc='Husband''s Income ($1000s)'; label rh='Partial Residual [Working]'; run; quit;
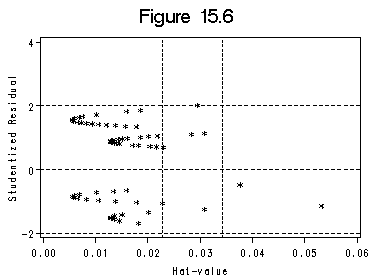
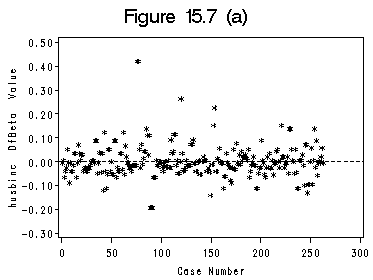
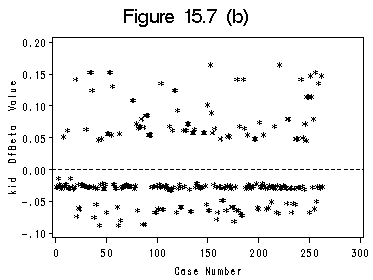
Figure 15.6 and Figure 15.7 (a) and (b). We use SAS ODS to output the influence statistics to a data file. Index plots of Dfbeta are basically the plots presented in Figure (a) and (b).
proc logistic data=wcoded; model wstatus=husbinc kid/influence ; ods output Influence=winf; run; data winf1; set winf; g=ResDev/sqrt(1-HatDiag); /*creating studentized residaul*/ run; proc means data=winf; /*get coordinate for the reference lines*/ var HatDiag; run; axis1 order =(0 to 0.06 by 0.01); axis2 order =(-2 to 4 by 2) label=(r=0 a=90); symbol c=black i=none v=star h=0.8; title 'Figure 15.6'; proc gplot data=winf1; format HatDiag f4.2 ; plot g*HatDiag =1 / href =(.02282 .03423) lhref=2 vref=(-2 0 2) lvref=2 haxis=axis1 vaxis=axis2 hminor=0 vminor=0; label HatDiag='Hat-value'; label g='Studentized Residual'; run; quit;
axis1 order =(0 to 300 by 50); axis2 order =(-0.3 to 0.5 by 0.1) label=(r=0 a=90); symbol c=black i=none v=star h=0.8; title 'Figure 15.7 (a)'; proc gplot data=winf1; format CaseNum f4.0 husbincDfbeta f5.2; plot husbincDfbeta*CaseNum /haxis=axis1 vaxis=axis2 vref=(0) lvref=2 hminor=0 vminor=0; run; quit;
axis1 order =(0 to 300 by 50); axis2 order =(-0.1 to 0.2 by 0.05) label=(r=0 a=90); symbol c=black i=none v=star h=0.8; title 'Figure 15.7 (b)'; proc gplot data=winf; format kidDfbeta f4.2; plot kidDfbeta*CaseNum /haxis=axis1 vaxis=axis2 vref=(0) lvref=2 hminor=0 vminor=0;; run; quit;
proc logistic data=wcoded descending; /*rerunning proc logistic without observation 76 and 77*/ model wstatus=husbinc kid ; where obs ne 76 and obs ne 77 ; run; quit;
The LOGISTIC Procedure
(Some output omitted here.)
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.6090 0.4052 15.7638 <.0001
husbinc 1 0.0603 0.0212 8.1089 0.0044
kid 1 1.6476 0.2978 30.6071 <.0001
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
husbinc 1.062 1.019 1.107
kid 5.194 2.898 9.312
Section 15.2 Models for Polytomous Data
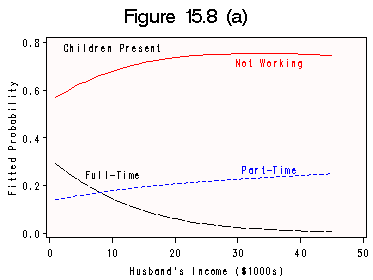
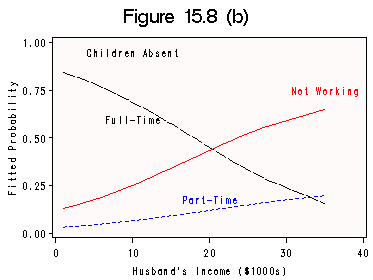
Calculation on page 468 and Figure 15.8 (a) and (b) on data file womenlf. We still use the same code scheme from last section.
proc catmod data=wcoded; direct husbinc kid;/*to specify that they are continuous variables*/ model w = husbinc kid / oneway noresponse;/*Can tell baseline from oneway table*/ response out=catout; run; data catplot; set catout; array p(3); array q(3); if _type_ eq 'PROB' and kid=0 then p(_number_)=_pred_; if _type_ eq 'PROB' and kid=1 then q(_number_)=_pred_; keep p1 p2 p3 q1 q2 q3 husbinc; output; run; data lab1; length function style $ 8 text $17; retain function 'label' xsys ysys '2' when 'a' color 'black'; function='label'; x=10; y=0.78; size=1; color='black'; text='Children Present'; output; function='label'; x=35; y=0.72; size=1; color='red'; text='Not Working'; output; function='label'; x=35; y=.27; size=1; color='blue'; text='Part-Time'; output; function='label'; x=10; y=0.25; size=1; color='black'; text='Full-Time'; output; run; title 'Figure 15.8 (a)'; axis1 order=(0 to 50 by 10); axis2 order=(0 to 0.8 by .2) label =(r=0 a =90); symbol1 c=black v=none line=4 h=1 i=join; symbol2 c=blue v=none line=2 h=1 i = join; symbol3 c=red v=none line=1 h=1 i=join; proc gplot data=catplot; plot q1*husbinc=1 q2*husbinc=2 q3*husbinc=3 /annotate=lab1 overlay hminor=0 vminor=0 haxis=axis1 vaxis=axis2 cframe=snow; label husbinc='Husband''s Income ($1000s)'; label q1='Fitted Probability'; run; quit;
data lab2; length function style $ 8 text $17; retain function 'label' xsys ysys '2' when 'a' color 'black'; function='label'; x=10; y=0.95; size=1; color='black'; text='Children Absent'; output; function='label'; x=35; y=0.75; size=1; color='red'; text='Not Working'; output; function='label'; x=20; y=.18; size=1; color='blue'; text='Part-Time'; output; function='label'; x=10; y=0.60; size=1; color='black'; text='Full-Time'; output; run; title 'Figure 15.8 (b)'; axis1 order=(0 to 40 by 10); axis2 order=(0 to 1 by .25) label =(r=0 a =90); symbol1 c=black v=none line=4 h=1 i=join; symbol2 c=blue v=none line=2 h=1 i = join; symbol3 c=red v=none line=1 h=1 i=join; proc gplot data=catplot; plot p1*husbinc=1 p2*husbinc=2 p3*husbinc=3 /annotate=lab2 haxis=axis1 vaxis=axis2 overlay hminor=0 vminor=0 cframe=snow; label husbinc='Husband''s Income ($1000s)'; label p1='Fitted Probability'; run; quit;
The CATMOD Procedure
Response w Response Levels 3
Weight Variable None Populations 46
Data Set WCODED Total Frequency 263
Frequency Missing 0 Observations 263
One-Way Frequencies
Variable Value Frequency
-----------------------------
w 0 66
1 42
2 155 <---This is the value for baseline.
(More output omitted here.)
Maximum Likelihood Analysis
Sub -2 Log Convergence
Iteration Iteration Likelihood Criterion
---------------------------------------------------
0 0 577.87006 1.0000
1 0 430.05981 0.2558
2 0 423.04966 0.0163
3 0 422.88205 0.000396
4 0 422.88193 2.9496E-7
5 0 422.88193 4.418E-13
Maximum Likelihood Analysis
Parameter Estimates
Iteration 1 2 3 4 5 6
---------------------------------------------------------------------------------------
0 0 0 0 0 0 0
1 1.6451 -0.5022 -0.0616 -0.0152 -2.5035 -0.8029
2 1.8666 -1.3618 -0.0900 0.007921 -2.4978 -0.0311
3 1.9801 -1.4285 -0.0971 0.006855 -2.5570 0.0185
4 1.9828 -1.4323 -0.0972 0.006892 -2.5586 0.0215
5 1.9828 -1.4323 -0.0972 0.006892 -2.5586 0.0215
Maximum likelihood computations converged.
Maximum Likelihood Analysis of Variance
Source DF Chi-Square Pr > ChiSq
--------------------------------------------------
Intercept 2 29.35 <.0001
husbinc 2 12.82 0.0016
kid 2 53.98 <.0001
Likelihood Ratio 86 138.67 0.0003
Analysis of Maximum Likelihood Estimates
Standard Chi-
Effect Parameter Estimate Error Square Pr > ChiSq
-----------------------------------------------------------------------
Intercept 1 1.9828 0.4842 16.77 <.0001
2 -1.4323 0.5925 5.84 0.0156
husbinc 3 -0.0972 0.0281 11.98 0.0005
4 0.00689 0.0235 0.09 0.7689
kid 5 -2.5586 0.3622 49.90 <.0001
6 0.0215 0.4690 0.00 0.9635
Calculation on nested dichotomies in subsection 15.2.2. Notice that in SAS proc logistic the option rsq on the model statement gives generalized R-sqaure, which is not the same as in the book. The second proc logistic below is for the purpose of computing (G0)2 at the bottom of the page using -2*Log L.
proc logistic data=wcoded; /* [15.27]*/ model wstatus =husbinc kid/rsq; test husbinc; /*returns Wald test*/ run; proc logistic data=wcoded; model wstatus = kid /rsq; run;
The LOGISTIC Procedure ---[15.27]
(Most of the output is omitted here.)
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 358.151 325.733
SC 361.723 336.449
-2 Log L 356.151 319.733 <--Needed for likelihood-ratio test
R-Square 0.1293 Max-rescaled R-Square 0.1743 <--generalized R-square
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 1.3358 0.3838 12.1164 0.0005
husbinc 1 -0.0423 0.0198 4.5750 0.0324
kid 1 -1.5756 0.2923 29.0650 <.0001
Linear Hypotheses Testing Results <-- Wald test on the effect of income
Wald
Label Chi-Square DF Pr > ChiSq
Test 1 4.5750 1 0.0324
The LOGISTIC Procedure --for the likelihood-ratio test on the effect on income
(Most of the output is omitted here.)
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 358.151 328.559
SC 361.723 335.703
-2 Log L 356.151 324.559 <--Needed for likelihood-ratio test
R-Square 0.1132 Max-rescaled R-Square 0.1526
data wcode1; /*full-time vs. part-time*/ set womenlf; if (work='fulltime') then wstatus=1; else if (work = 'parttime') then wstatus=0; if (child ='present') then kid = 1; else kid =0; run; proc logistic data=wcode1 descending;/*formula on p. 473: part-time vs. full-time*/ model wstatus= husbinc kid /rsq;
The LOGISTIC Procedure --full-time vs. part-time
(Most of the output omitted here.)
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 146.342 110.495
SC 149.024 118.541
-2 Log L 144.342 104.495
R-Square 0.3085 Max-rescaled R-Square 0.4185
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 39.8468 2 <.0001
Score 35.1502 2 <.0001
Wald 25.5820 2 <.0001
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 3.4778 0.7671 20.5536 <.0001
husbinc 1 -0.1073 0.0392 7.5062 0.0061
kid 1 -2.6514 0.5411 24.0134 <.0001
data wcode2; set womenlf; if (work='not_work') then w=2; else if (work='fulltime') then w=0; else w=1; if (child ='present') then kid = 1; else kid =0; ik=husbinc*kid; run; proc logistic data=wcode2; model w=husbinc kid / rsq ; run;
The LOGISTIC Procedure
(Most of the output is omitted here.)
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 504.493 449.663
SC 511.637 463.952
-2 Log L 500.493 441.663
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 58.8296 2 <.0001
Score 54.6338 2 <.0001
Wald 53.9013 2 <.0001
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 0.9409 0.3619 6.7579 0.0093
Intercept2 1 1.8520 0.3773 24.0994 <.0001
husbinc 1 -0.0539 0.0194 7.6913 0.0055
kid 1 -1.9719 0.2804 49.4637 <.0001
Section 15.3 Discrete Independent Variables and Contingency Tables
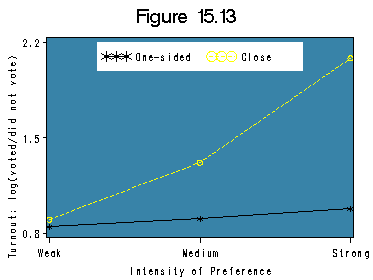
The analysis in this section is based on Table 15.3, which is based on data from an example from The American Voter (Campbell et al. 1960). The first dataset is created based on Table 15.3 for Figure 15.13.
data logvote;
input logv_one logv_close intensity;
label intensity ='0 for weak, 1 for medium and 2 for strong';
datalines;
.847 .9 0
.904 1.318 1
.981 2.084 2
;
run;
title 'Figure 15.13';
filename outfiles 'https://stats.idre.ucla.edu/wp-content/uploads/2016/02/chp15Fig13.gif';
axis1 label =(r=0 a=90) order=(0.8 to 2.2 by .7);
axis2 value=('Weak' 'Medium' 'Strong');
symbol1 c=black v=star i=join line=1 ;
symbol2 c=yellow v=circle i=join line=2;
legend1 label=none
shape=symbol(4,2)
cframe=white
position=(top center inside)
value=('One-sided' 'Close')
mode=share;
proc gplot data=logvote;
plot logv_one*intensity=1 logv_close*intensity=2 /
overlay vaxis=axis1 haxis=axis2 vminor=0 hminor=0 lengend=lengend1 cframe=steel;
label intensity='Intensity of Preference';
label logv_one = 'Turnout: log(voted/did not vote)';
run;
quit;
In order to do the logistic regression, we create another dataset based on Table 15.3 again using the turnout frequencies as weight. For Table 15.4 and Table 15.5 we run proc logistic for each model and obtain (G0)2 by taking the difference of -2*Log L from each pair models being compared. Table 15.5 is produced in the last data step and proc print using SAS function probchi.
data election; input perclose inten1 inten2 voted wv; label perclose ='0 for one-sided 1 for close' intens1 ='baseline: weak' voted = '0 for not 1 for yes'; clspref1=perclose*inten1; clspref2=perclose*inten2; cards; 0 0 0 1 91 0 0 0 0 39 0 1 0 1 121 0 1 0 0 49 0 0 1 1 64 0 0 1 0 24 1 0 0 1 214 1 0 0 0 87 1 1 0 1 284 1 1 0 0 76 1 0 1 1 201 1 0 1 0 25 ; run; proc logistic data=election; /*model 1*/ model voted = perclose inten1 inten2 clspref1 clspref2; weight wv; test: test clspref1=0, clspref2=0; run; proc logistic data=election; /*model 2*/ model voted = perclose inten1 inten2; weight wv; run; proc logistic data=election; /*model 3*/ model voted = perclose clspref1 clspref2; weight wv; run; proc logistic data=election; /*model 4*/ model voted = inten1 inten2 clspref1 clspref2; weight wv; run; proc logistic data=election; /*model 5*/ model voted = perclose; weight wv; run; proc logistic data=election; /*model 6*/ model voted = inten1 inten2; weight wv; run;
(Most of the output is omitted here.)
The LOGISTIC Procedure --Model 1--
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
-2 Log L 1391.266 1356.434
The LOGISTIC Procedure --Model 2--
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
-2 Log L 1391.266 1363.553
The LOGISTIC Procedure --Model 3--
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
-2 Log L 1391.266 1356.625
The LOGISTIC Procedure --Model 4--
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
-2 Log L 1391.266 1356.487
The LOGISTIC Procedure --Model 5--
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
-2 Log L 1391.266 1382.658
The LOGISTIC Procedure --Model 6--
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
-2 Log L 1391.266 1371.838
data logL; input models $ df g1 g2 @g p; g=g1-g2; p=1-probchi(g1-g2,df); drop g1 g2; cards; 6-2 1 1371.838 1363.552 4-1 1 1356.487 1356.434 5-2 2 1382.658 1363.552 3-1 2 1356.625 1356.434 2-1 2 1363.552 1356.434 ; run; proc print data=logL; run;
Obs models df g p 1 6-2 1 8.286 0.00400 2 4-1 1 0.053 0.81792 3 5-2 2 19.106 0.00007 4 3-1 2 0.191 0.90892 5 2-1 2 7.118 0.02847