In this chapter we will be using the hmohiv and the uis data sets.
Creating all the dummy variables for the covariates in the UIS data.
data uis; set uis; hercoc1 = (hercoc=1); hercoc2 = (hercoc=2); hercoc3 = (hercoc=3); hercoc4 = (hercoc=4); ivhx1 = (ivhx = 1); ivhx2 = (ivhx = 2); ivhx3 = (ivhx = 3); agecat = 0; if age < 28 then agecat = 1; else if age < 33 then agecat = 2; else if age < 38 then agecat = 3; else agecat = 4; agecat1 = (age < 28); agecat2 = (age >= 28 & age < 33); agecat3 = (age >= 33 & age < 38); agecat4 = (age >= 38); beckcat = 0; if becktota < 10 then beckcat = 1; else if becktota < 15 then beckcat = 2; else if becktota < 25 then beckcat = 3; else beckcat = 4; beckcat1 = (becktota < 10); beckcat2 = (becktota >= 10 & becktota < 15); beckcat3 = (becktota >= 15 & becktota < 25); beckcat4 = (becktota >= 25); drugcat = 0; if ndrugtx < 2 then drugcat = 1; else if ndrugtx < 4 then drugcat = 2; else if ndrugtx < 7 then drugcat = 3; else drugcat = 4; drugcat1 = (ndrugtx < 2); drugcat2 = (ndrugtx >= 2 & ndrugtx < 4); drugcat3 = (ndrugtx >= 4 & ndrugtx < 7); drugcat4 = (ndrugtx >= 7); run;
Table 5.1, p. 166.
Estimated median time to drug use and Log Rank test for categorical covariates in the UIS data.
proc lifetest data=uis;
time time*censor(0);
strata hercoc;
run;
<output omitted>
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 14.7196 2 0.0006
Quartile Estimates
Stratum 1: hercoc = 1
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 150.00 106.00 196.00
Stratum 2: hercoc = 2
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 146.50 110.00 184.00
Stratum 3: hercoc = 3
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 184.50 148.00 226.00
Stratum 4: hercoc = 4
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 181.00 154.00 220.00
proc lifetest data=uis;
time time*censor(0);
strata ivhx;
run;
<output omitted>
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 14.7196 2 0.0006
Quartile Estimates
Stratum 1: ivhx = 1
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 194.00 171.00 228.00
Stratum 2: ivhx = 2
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 170.00 130.00 226.00
Stratum 3: ivhx = 3
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 147.50 115.00 168.00
proc lifetest data=uis;
time time*censor(0);
strata race;
run;
<output omitted>
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 7.2836 1 0.0070
Quartile Estimates
Stratum 1: race = 0
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 152.00 124.00 174.00
Stratum 2: race = 1
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 193.00 164.00 232.00
proc lifetest data=uis;
time time*censor(0);
strata treat;
run;
<output omitted>
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 6.7979 1 0.0091
Quartile Estimates
Stratum 1: treat = 0
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 131.50 113.00 154.00
Stratum 2: treat = 1
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 192.00 175.00 226.00
proc lifetest data=uis;
time time*censor(0);
strata site;
run;
<output omitted>
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 2.3658 1 0.1240
Quartile Estimates
Stratum 1: site = 0
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 156.00 131.00 174.00
Stratum 2: site = 1
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 199.00 159.00 231.00
proc lifetest data=uis;
time time*censor(0);
strata agecat;
run;
<output omitted>
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 3.9295 3 0.2692
Quartile Estimates
Stratum 1: agecat = 1
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 144.00 121.00 190.00
Stratum 2: agecat = 2
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 148.00 123.00 180.00
Stratum 3: agecat = 3
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 163.00 121.00 207.00
Stratum 4: agecat = 4
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 189.00 162.00 242.00
proc lifetest data=uis;
time time*censor(0);
strata beckcat;
run;
<output omitted>
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 1.6152 3 0.6559
Quartile Estimates
Stratum 1: beckcat = 1
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 170.00 129.00 211.00
Stratum 2: beckcat = 2
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 169.50 130.00 220.00
Stratum 3: beckcat = 3
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 168.00 137.00 199.00
Stratum 4: beckcat = 4
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 145.50 110.00 190.00
proc lifetest data=uis;
time time*censor(0);
strata drugcat;
run;
<output omitted>
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 15.2189 3 0.0016
Quartile Estimates
Stratum 1: drugcat = 1
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 175.00 142.00 226.00
Stratum 2: drugcat = 2
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 177.00 162.00 207.00
Stratum 3: drugcat = 3
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 131.50 106.00 183.00
Stratum 4: drugcat = 4
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
50 123.00 106.00 184.00
Table 5.2, p. 167.
The estimated hazard ratio and partial likelihood ratio test for continuous covariates in the UIS data.
data uis;
set uis;
age5 = age/5;
beck10 = becktota / 10;
ndrugtx5 = ndrugtx / 5;
run;
proc phreg data=uis;
model time*censor(0) = age5 / rl;
run;
<output omitted>
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard 95% Hazard Ratio
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio Confidence Limits
age5 1 -0.06432 0.03594 3.2022 0.0735 0.938 0.874 1.006
proc phreg data=uis;
model time*censor(0) = beck10 / rl;
run;
<output omitted>
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard 95% Hazard Ratio
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio Confidence Limits
beck10 1 0.10962 0.04715 5.4045 0.0201 1.116 1.017 1.224
proc phreg data=uis;
model time*censor(0) = ndrugtx5 / rl;
run;
<output omitted>
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard 95% Hazard Ratio
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio Confidence Limits
ndrugtx5 1 0.14686 0.03749 15.3470 <.0001 1.158 1.076 1.247
Table 5.3, p. 168.
Proportional hazard model containing all the covariates that were significant at the 20% level in the bivariate analysis.
proc phreg data=uis;
model time*censor(0) = age becktota ndrugtx hercoc2 hercoc3 hercoc4 ivhx2 ivhx3
race treat site;
run;
<output omitted>
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
age 1 -0.02887 0.00817 12.4833 0.0004 0.972
becktota 1 0.00834 0.00498 2.8109 0.0936 1.008
ndrugtx 1 0.02837 0.00831 11.6692 0.0006 1.029
hercoc2 1 0.06532 0.15001 0.1896 0.6633 1.067
hercoc3 1 -0.09362 0.16547 0.3201 0.5715 0.911
hercoc4 1 0.02798 0.16028 0.0305 0.8614 1.028
ivhx2 1 0.17439 0.13864 1.5822 0.2084 1.191
ivhx3 1 0.28071 0.14693 3.6501 0.0561 1.324
race 1 -0.20289 0.11669 3.0232 0.0821 0.816
treat 1 -0.23995 0.09437 6.4648 0.0110 0.787
site 1 -0.10249 0.10927 0.8798 0.3483 0.903
Table 5.4, p. 168.
Reduced proportional hazard model (eliminating hercoc1-hercoc3).
proc phreg data=uis;
model time*censor(0) = age becktota ndrugtx ivhx2 ivhx3 race treat site;
run;
<output omitted>
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
age 1 -0.02822 0.00817 11.9285 0.0006 0.972
becktota 1 0.00794 0.00497 2.5541 0.1100 1.008
ndrugtx 1 0.02776 0.00829 11.2265 0.0008 1.028
ivhx2 1 0.19599 0.13721 2.0402 0.1532 1.217
ivhx3 1 0.33280 0.11991 7.7025 0.0055 1.395
race 1 -0.20925 0.11589 3.2598 0.0710 0.811
treat 1 -0.23177 0.09371 6.1169 0.0134 0.793
site 1 -0.09946 0.10854 0.8397 0.3595 0.905
Table 5.5, p. 169.
Further reduced proportional hazard model (eliminating ivhx2).
proc phreg data=uis;
model time*censor(0) = age becktota ndrugtx ivhx3 race treat site;
run;
<output omitted>
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
age 1 -0.02615 0.00805 10.5563 0.0012 0.974
becktota 1 0.00840 0.00495 2.8762 0.0899 1.008
ndrugtx 1 0.02907 0.00821 12.5338 0.0004 1.030
ivhx3 1 0.25612 0.10630 5.8053 0.0160 1.292
race 1 -0.22446 0.11527 3.7922 0.0515 0.799
treat 1 -0.23243 0.09373 6.1488 0.0132 0.793
site 1 -0.08669 0.10786 0.6459 0.4216 0.917
Likelihood test comparing models in table 5.4 and 5.5, p. 169. The test statistic G = 5283.459 - 5281.456 = 2.003. There is only one more predictor in the larger model so the test statistic is compared to a chi-square distribution with one degree of freedom which results in a p-value of .157. So, the larger model is not better than the smaller model and the extra predictor does not improve the fit of the model.
Table 5.6, p. 170. Notice that the coding done in the data step to recode some variables into categorical variables does not take into the account that the variables may have missing values. To correctly use the categorical version of them, we will have to eliminate these missing observations. This is what the where statement in the following procedure for.
proc phreg data=uis;
where age~=. and becktota~=. and ndrugtx~=. and ivhx~=.;
model time*censor(0) = agecat2 agecat3 agecat4 beckcat2 beckcat3 beckcat4
drugcat2 drugcat3 drugcat4 ivhx3 race treat site;
run;
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
agecat2 1 0.03738 0.13165 0.0806 0.7764 1.038 agecat3 1 -0.24098 0.13123 3.3721 0.0663 0.786 agecat4 1 -0.40041 0.15068 7.0614 0.0079 0.670 beckcat2 1 0.04642 0.15268 0.0924 0.7611 1.048 beckcat3 1 0.10783 0.12496 0.7446 0.3882 1.114 beckcat4 1 0.20975 0.14029 2.2353 0.1349 1.233 drugcat2 1 -0.09153 0.12945 0.4999 0.4795 0.913 drugcat3 1 0.24268 0.13369 3.2953 0.0695 1.275 drugcat4 1 0.37056 0.14043 6.9634 0.0083 1.449 ivhx3 1 0.24173 0.10678 5.1248 0.0236 1.273 race 1 -0.25113 0.11637 4.6571 0.0309 0.778 treat 1 -0.21733 0.09414 5.3297 0.0210 0.805 site 1 -0.08353 0.10846 0.5932 0.4412 0.920
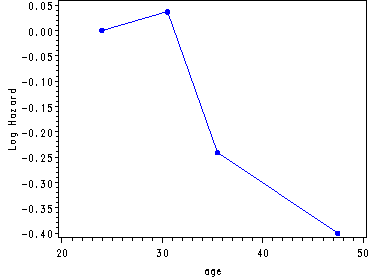
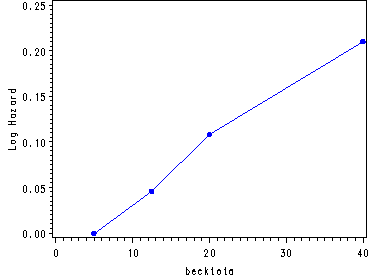
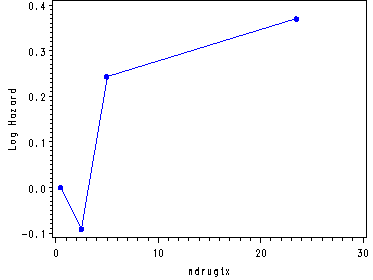
Inputting the values from table 5.6, p. 170 in order to generate fig. 5.1, p. 171.
data midpoints; input age c1 becktota c2 ndrugtx c3; cards; 24 0 5 0 .5 0 30.5 .037 12.5 .046 2.5 -.091 35.5 -.241 20 .108 5 .243 47.5 -.400 40 .210 23.5 .370 ; run; goptions reset = all; symbol c=blue v=dot h=.8 i=j; axis1 order=(-.4 to .05 by .05) label=(a=90 'Log Hazard'); axis2 order=(0 to .25 by .05) label=(a=90 'Log Hazard'); axis3 order=(-.1 to .4 by .1) label=(a=90 'Log Hazard'); proc gplot data=midpoints; plot c1*age / vaxis=axis1; plot c2*becktota / vaxis=axis2; plot c3*ndrugtx / vaxis=axis3; run; quit;
Creating ndrugfp1 and ndrugfp2.
data uis; set uis; ndrugfp1 = 1/((ndrugtx+1)/10); ndrugfp2 = (1/((ndrugtx+1)/10))*log((ndrugtx+1)/10); run;
Table 5.8, p. 169.
Proportional hazard model including ndrugfp1 and ndrugfp2.
proc phreg data=uis; model time*censor(0) = age becktota ndrugfp1 ndrugfp2 ivhx3 race treat site; run; <output omitted> Analysis of Maximum Likelihood Estimates Parameter Standard Hazard Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio age 1 -0.02815 0.00813 11.9807 0.0005 0.972 becktota 1 0.00916 0.00499 3.3754 0.0662 1.009 ndrugfp1 1 -0.52284 0.12441 17.6610 <.0001 0.593 ndrugfp2 1 -0.19478 0.04825 16.2999 <.0001 0.823 ivhx3 1 0.25858 0.10802 5.7299 0.0167 1.295 race 1 -0.24220 0.11547 4.3998 0.0359 0.785 treat 1 -0.21084 0.09369 5.0644 0.0244 0.810 site 1 -0.10532 0.10915 0.9310 0.3346 0.900
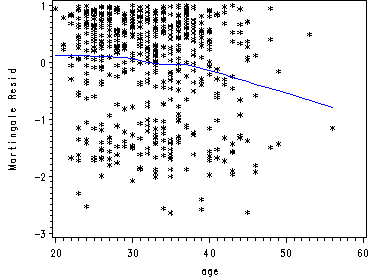
Generating the plots of the martingale residuals and the lowess smoothed residuals. First we run the model in using proc phreg without age. Then we output the martingale residuals using the output statement with a resmart option. Since this data set does not include age because age was not in the model we must merge the outputted data set with a copy of the UIS data set containing age. We choose to merge on time and therefore we sort both data sets on time and then merge them. Then we run the proc loess on the combined data set, regressing age on the martingale residuals with a smoothing factor of 0.65. Then we plot the residuals and the lowess smoothed residuals.
proc phreg data=uis noprint; model time*censor(0) = becktota ndrugtx ivhx3 race treat site; output out=residuals resmart=resmart; run; proc sort data=residuals; by time; run; data age; set uis; keep time age; run; proc sort data=age; by time; run; data residage; merge residuals age; by time; run; ods listing close; proc loess data=residage; model resmart = age /smooth=0.65; ods output OutputStatistics=myout; run; ods listing; quit; proc sort data=myout; by age; run; goptions reset=all; symbol1 c = black i=none v=star h=0.8; symbol2 c=blue i=join v=none; axis label=(a=90 'Martingale Resid'); proc gplot data=myout; format DepVar f4.0 age f4.0; plot DepVar*age=1 Pred*age=2 /overlay vaxis=axis1 ; run; quit;
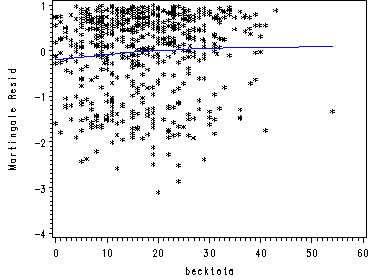
Fig. 5.3a, p. 176.
Martingal residuals and lowess smoothed residuals.
proc phreg data=uis noprint; model time*censor(0) = age ndrugtx ivhx3 race treat site; output out=residuals resmart=resmart; run; proc sort data=residuals; by time; run; data becktota; set uis; keep time becktota; run; proc sort data=becktota; by time; run; data residbeck; merge residuals becktota; by time; run; ods listing close; proc loess data=residbeck; model resmart = becktota /smooth=0.8; ods output OutputStatistics=myout; run; quit; ods listing; proc sort data=myout; by becktota; run; goptions reset=all; symbol1 c = black i=none v=star h=0.7; symbol2 c=blue i=join v=none; axis label=(a=90 'Martingale Resid'); proc gplot data=myout; format DepVar f4.0 becktota f4.0; plot DepVar*becktota=1 Pred*becktota=2 /overlay vaxis=axis1 ; run; quit;
Fig. 5.4a, p. 176.
Martingal residuals and lowess smoothed residuals.
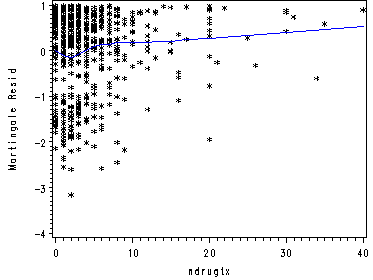
proc phreg data=uis noprint; model time*censor(0) = age becktota ivhx3 race treat site; output out=residuals resmart=resmart; run; proc sort data=residuals; by time; run; data ndrugtx; set uis; keep time ndrugtx; run; proc sort data=ndrugtx; by time; run; data residdrug; merge residuals ndrugtx; by time; run; ods listing close; proc loess data=residdrug; model resmart = ndrugtx /smooth=0.6; ods output OutputStatistics=myout; run; quit; ods listing; proc sort data=myout; by ndrugtx; run; goptions reset=all; symbol1 c = black i=none v=star h=0.8; symbol2 c=blue i=join v=none; axis label=(a=90 'Martingale Resid'); proc gplot data=myout; format DepVar f4.0 ndrugtx f4.0; plot DepVar*ndrugtx=1 Pred*ndrugtx=2 /overlay vaxis=axis1 ; run; quit;
Table 5.10, p. 179.
Preliminary interaction variables proportional hazards model.
data interaction; set uis; agefp1 = age*ndrugfp1 ; agefp2 = age*ndrugfp2 ; racesite = race*site ; agesite = age*site; run; proc phreg data=interaction; model time*censor(0) = age becktota ndrugfp1 ndrugfp2 ivhx3 race treat site agefp1 agefp2 racesite agesite; run; <output omitted> Analysis of Maximum Likelihood Estimates Parameter Standard Hazard Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio treat 1 -0.24205 0.09455 6.5534 0.0105 0.785 site 1 -1.11940 0.54607 4.2021 0.0404 0.326 agefp1 1 0.00163 0.01945 0.0070 0.9332 1.002 agefp2 1 -0.00198 0.00766 0.0670 0.7957 0.998 racesite 1 0.86274 0.24810 12.0919 0.0005 2.370 agesite 1 0.02644 0.01658 2.5437 0.1107 1.027
Table 5.11, p. 179.
Preliminary Final proportional hazard model for UIS data.
proc phreg data=interaction; model time*censor(0) = age becktota ndrugfp1 ndrugfp2 ivhx3 race treat site racesite agesite; run; <output omitted> Analysis of Maximum Likelihood Estimates Parameter Standard Hazard Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio treat 1 -0.24676 0.09434 6.8416 0.0089 0.781 site 1 -1.31699 0.53144 6.1412 0.0132 0.268 racesite 1 0.85028 0.24776 11.7778 0.0006 2.340 agesite 1 0.03240 0.01608 4.0596 0.0439 1.033
Table 5.15, p. 192.
Using the best subset selection based on the score test by utilizing the option selection = score, the best option specifies that we want only the two best models from each subset, the start and stop options specify that we want to obtain models only from the subsets that contain 5 to 8 predictors.
proc phreg data=interaction;
model time*censor(0) = age becktota ndrugtx ivhx3 race treat site ivhx2 hercoc1 hercoc2 hercoc3
/ selection=score best=2 start=5 stop = 8;
run;
<output omitted>
The PHREG Procedure
Regression Models Selected by Score Criterion
Number of Score
Variables Chi-Square Variables Included in Model
5 42.8329 age ndrugtx ivhx3 race treat
5 42.2824 age ndrugtx ivhx3 treat ivhx2
6 45.5216 age becktota ndrugtx ivhx3 race treat
6 44.9214 age ndrugtx ivhx3 race treat ivhx2
7 47.3567 age becktota ndrugtx ivhx3 race treat ivhx2
7 47.1510 age becktota ndrugtx ivhx3 race treat hercoc3
8 48.4974 age becktota ndrugtx ivhx3 race treat ivhx2 hercoc3
8 47.9901 age becktota ndrugtx ivhx3 race treat site ivhx2