In this chapter we will be using the hmohiv and the uis data sets.
Fig. 2.1, p. 28.
The first five observations of the hmohiv data set.
data mini; set hmohiv; if id <= 5 ; run; proc print data=mini noobs; var id time censor; run;
ID time censor 1 5 1 2 6 0 3 8 1 4 3 1 5 22 1
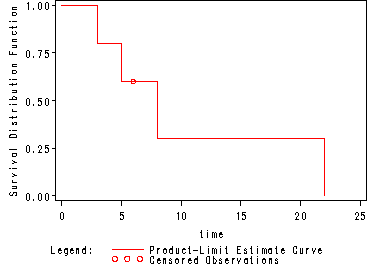
Table 2.2 and fig. 2.1, p. 32.
The estimated survivorship function computed for the mini data set in table 2.1, p. 28.
Note: The graph was generated by using the options plot=(s) where s=survival curve.
proc lifetest data=mini plots=(s);
time time*censor(0);
run;
<output omitted>
Product-Limit Survival Estimates
Survival
Standard Number Number
time Survival Failure Error Failed Left
0.0000 1.0000 0 0 0 5
3.0000 0.8000 0.2000 0.1789 1 4
5.0000 0.6000 0.4000 0.2191 2 3
6.0000* . . . 2 2
8.0000 0.3000 0.7000 0.2387 3 1
22.0000 0 1.0000 0 4 0
NOTE: The marked survival times are censored observations.
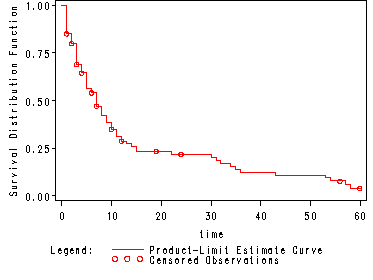
Fig. 2.2, p. 34.
The figure shows the Kaplan-Meier estimate of the survivorship function.
Note: We use the ods output system to create a data set est containing the Kaplan-Meier estimates and the components used in calculating the estimates.
ods listing close; ods output ProductLimitEstimates=est; proc lifetest data=hmohiv plots=(s); time time*censor(0); run; ods listing;
Table 2.3, p. 35.
Note: The output from proc lifetest has one line of output for each subject. In other words there would be 15 lines of output before the line containing the first estimate. We eliminate this extra output by including a where statement in the proc print stipulating that we do not wish to see the output where there is no Kaplan-Meier estimate.
proc print data=est noobs; where survival ne . ; var time left failed survival; run; <output omitted> time Left Failed Survival 0.0000 100 0 1.0000 1.0000 85 15 0.8500 2.0000 78 20 0.7988 3.0000 63 30 0.6894 4.0000 57 34 0.6442 5.0000 49 41 0.5636 ... 57.0000 3 79 0.0584 58.0000 2 80 0.0389
In order to get other variables in the table, we will have to use a couple of data steps.
ods listing close;
ods output ProductLimitEstimates=t2;
proc lifetest data=hmohiv outs=t ;
time time*censor(0);
run;
ods listing;
data t2a;
set t2;
retain c 0;
retain s 1;
by time;
if first.time & _n_ >1 then c = censor;
else if _n_ > 1 then c = c + censor;
if survival ~=. then s = survival;
keep time failed left c s ;
if last.time;
run;
data t2b; set t2a; flag = lag(failed); d = failed-flag; llag = lag(left); s1 = (llag -d)/llag; drop flag llag; run; proc print data = t2b noobs; var time left d c s1 s; run;
time Left d c s1 s 0.0000 100 . 0 . 1.00000 1.0000 83 15 2 0.85000 0.85000 2.0000 73 5 5 0.93976 0.79880 3.0000 61 10 2 0.86301 0.68937 4.0000 56 4 1 0.93443 0.64417 5.0000 49 7 0 0.87500 0.56365 6.0000 46 2 1 0.95918 0.54064 7.0000 39 6 1 0.86957 0.47012 8.0000 35 4 0 0.89744 0.42190 9.0000 32 3 0 0.91429 0.38574 10.0000 28 3 1 0.90625 0.34958 11.0000 25 3 0 0.89286 0.31212 12.0000 21 2 2 0.92000 0.28715 13.0000 20 1 0 0.95238 0.27348 14.0000 19 1 0 0.95000 0.25981 15.0000 17 2 0 0.89474 0.23246 19.0000 16 0 1 1.00000 0.23246 22.0000 15 1 0 0.93750 0.21793 24.0000 14 0 1 1.00000 0.21793 30.0000 13 1 0 0.92857 0.20236 31.0000 12 1 0 0.92308 0.18680 32.0000 11 1 0 0.91667 0.17123 34.0000 10 1 0 0.90909 0.15566 35.0000 9 1 0 0.90000 0.14010 36.0000 8 1 0 0.88889 0.12453 43.0000 7 1 0 0.87500 0.10896 53.0000 6 1 0 0.85714 0.09340 54.0000 5 1 0 0.83333 0.07783 56.0000 4 0 1 1.00000 0.07783 57.0000 3 1 0 0.75000 0.05837 58.0000 2 1 0 0.66667 0.03892 60.0000 0 0 2 1.00000 0.03892
Table 2.4, Figure 2.3 and Figure 2.4 on page 38 and page 39.
ods output LifetableEstimates=est2;
proc lifetest data=hmohiv method=lt intervals=(0 6 to 72 by 6);
time time*censor(0);
run;
proc print data = est2 noobs;
var lowertime uppertime failed censored effsize survival;
run;
Lower Upper Eff
Time Time Failed Censored Size Survival
0 6 41 10 95.0 1.0000
6 12 21 3 47.5 0.5684
12 18 6 2 24.0 0.3171
18 24 1 1 16.5 0.2378
24 30 0 1 14.5 0.2234
30 36 5 0 14.0 0.2234
36 42 1 0 9.0 0.1436
42 48 1 0 8.0 0.1277
48 54 1 0 7.0 0.1117
54 60 3 1 5.5 0.0958
60 66 0 2 1.0 0.0435
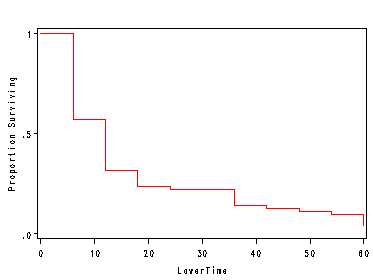
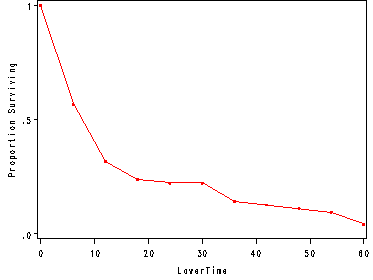
Fig. 2.3, p. 38.
symbol i = steplj c=red; axis1 label=( a= 90 "Proportion Surviving") minor=none order =(0 to 1 by .5); proc gplot data = est2; format survival 2.1; plot survival*lowertime / vaxis=axis1; run; quit;
symbol i = join c=red value=dot; axis1 label=( a= 90 "Proportion Surviving") minor=none order =(0 to 1 by .5); proc gplot data = est2; format survival 2.1; plot survival*lowertime / vaxis=axis1; run; quit;
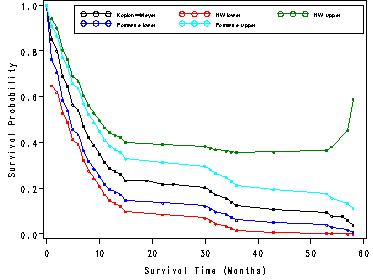
Fig. 2.5 on page 46. The code below works in SAS 9.1.3.
proc lifetest data=hmohiv noprint;
time time *censor(0);
survival out=Out1 confband=hw;
run;
symbol i=join v=circle r=5 ;
axis1 order = (0 to 1 by .2) label=(a=90 "Survival Probability") minor=none;
axis2 order = (0 to 60 by 10) label = ("Survival Time (Months)") minor=none;
legend label=none value=(h=2 font=swiss 'Kaplan-Meyer' 'HW lower' 'HW upper'
'Pointwise lower' 'Pointwise upper')
position=(top right inside) mode=share cborder=black;
proc gplot data = out1;
plot (survival hw_lcl hw_ucl sdf_lcl sdf_ucl)*time
/legend=legend1 vaxis=axis1 haxis=axis2 overlay;
run;
quit;
Table 2.5, p. 50.
proc lifetest data=hmohiv;
time time*censor(0);
run;
Quartile Estimates
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
75 15.0000 10.0000 34.0000
50 7.0000 5.0000 9.0000
25 3.0000 2.0000 4.0000
Table 2.6, p. 52.
proc lifetest data=hmohiv; time time*censor(0); survival out=out2; run; proc print data = out2 noobs; where 4<=time<=9 & conftype~=""; run;
time _CENSOR_ SURVIVAL CONFTYPE SDF_LCL SDF_UCL 4 0 0.64417 LOGLOG 0.53868 0.73150 5 0 0.56365 LOGLOG 0.45636 0.65769 6 0 0.54064 LOGLOG 0.43343 0.63609 7 0 0.47012 LOGLOG 0.36440 0.56876 8 0 0.42190 LOGLOG 0.31832 0.52174 9 0 0.38574 LOGLOG 0.28454 0.48579
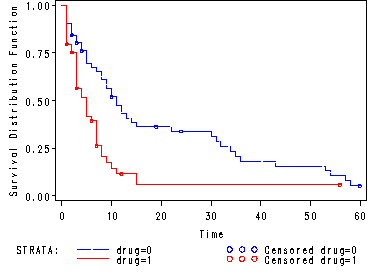
Fig. 2.7, p. 58.
Estimated survivorship functions for each group of drug use.
goptions reset = all; proc lifetest data=hmohiv plots=(s) noprint; time time*censor(0); strata drug; test age; run;
Table 2.8, p. 63.
Inputting the mini1 dataset.
data mini1; input time drug event; cards; 3 0 1 4 0 0 5 0 1 22 0 1 34 0 1 2 1 1 3 1 1 4 1 1 7 1 0 11 1 1 ; run; proc print data=mini1; run; time drug event 3 0 1 4 0 0 5 0 1 22 0 1 34 0 1 2 1 1 3 1 1 4 1 1 7 1 0 11 1 1
Table 2.9 on page 64. We will skip the data step for creating the d’s and n’s. Instead, we will focus on the calculation of other quantities in the table.
data table2_9; retain survival 1; input time d1 n1 d n; lagn = lag(n); lagd = lag(d); if _n_> 1 then survival = survival*(lagn+1-lagd)/(lagn+1); e = n1*d/n; v = n1*(n-n1)*d*(n-d)/(n**2*(n-1)); tw = sqrt(n); pp = survival*n/(n+1); lr = 1; wl = n; datalines; 2 0 5 1 10 3 1 5 2 9 4 0 4 1 7 5 1 3 1 5 11 0 2 1 3 22 1 2 1 2 34 1 1 1 1 ; run; proc print data = table2_9 noobs; var time d1 n1 d n e v lr wl tw pp; run;
time d1 n1 d n e v lr wl tw pp 2 0 5 1 10 0.50000 0.25000 1 10 3.16228 0.90909 3 1 5 2 9 1.11111 0.43210 1 9 3.00000 0.81818 4 0 4 1 7 0.57143 0.24490 1 7 2.64575 0.63636 5 1 3 1 5 0.60000 0.24000 1 5 2.23607 0.53030 11 0 2 1 3 0.66667 0.22222 1 3 1.73205 0.39773 22 1 2 1 2 1.00000 0.00000 1 2 1.41421 0.26515 34 1 1 1 1 1.00000 . 1 1 1.00000 0.13258
Table 2.10, p. 64.
Log-rank and Wilcoxon tests of equality of the survivorship functions across the two drug strata.
proc lifetest data=mini1; time time*event(0); strata drug /test=(logrank wilcoxon tarone peto modpeto); run;
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 1.5118 1 0.2189
Wilcoxon 1.2500 1 0.2636
Tarone 1.3632 1 0.2430
Peto 1.4229 1 0.2329
Modified Peto 1.3695 1 0.2419
Table 2.11, p. 65.
Testing for equality of survivorship functions across drug strata for the hmohiv data.
proc lifetest data=hmohiv; time time*censor(0); strata drug /test=(logrank wilcoxon tarone peto); run;
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 11.8556 1 0.0006
Wilcoxon 10.9104 1 0.0010
Tarone 12.3359 1 0.0004
Peto 11.4974 1 0.0007
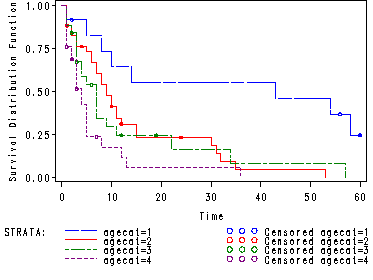
Table 2.12 , Figure 2.8, Table 2.14 and Table 2.15 on page 65, page 69 and page 70.
Creating the categorical variable for age.
data agecat; set hmohiv; if age le 29 then agecat = 1; else if age le 34 then agecat = 2; else if age le 39 then agecat = 3; else agecat = 4; run;
goptions reset=all;
proc lifetest data=agecat plots=(s);
time time*censor(0);
strata agecat /trend test=(logrank wilcoxon tarone peto);
symbol1 c=blue l=12 h=.5;
symbol2 c=red l=1 h=.5;
symbol3 c=green l=8 h=.5;
symbol4 c=purple l=2 h=.5;
run;
Summary of the Number of Censored and Uncensored Values
Percent
Stratum agecat Total Failed Censored Censored
1 1 12 8 4 33.33
2 2 34 29 5 14.71
3 3 25 20 5 20.00
4 4 29 23 6 20.69
-------------------------------------------------------------------
Total 100 80 20 20.0
Quartile Estimates
Stratum 1: agecat = 1
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
75 58.0000 43.0000 .
50 43.0000 8.0000 .
25 8.0000 5.0000 54.0000
Stratum 2: agecat = 2
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
75 15.0000 10.0000 32.0000
50 9.0000 7.0000 12.0000
25 5.0000 2.0000 8.0000
Stratum 3: agecat = 3
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
75 11.0000 7.0000 34.0000
50 7.0000 3.0000 9.0000
25 3.0000 2.0000 5.0000
Stratum 4: agecat = 4
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
75 5.0000 4.0000 13.0000
50 4.0000 3.0000 5.0000
25 2.0000 1.0000 3.0000
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 19.9058 3 0.0002
Wilcoxon 14.1433 3 0.0027
Tarone 16.9556 3 0.0007
Peto 15.6650 3 0.0013
Trend Tests
Test Standard
Test Statistic Error z-Score Pr > |z|
Log-Rank 34.3443 8.0563 4.2630 <.0001
Wilcoxon 1919.0000 517.5932 3.7075 0.0002
Tarone 243.3701 60.4948 4.0230 <.0001
Peto 18.8199 4.8370 3.8908 <.0001
Fig. 2.8, p. 69.
Table 2.17, p. 76.
proc phreg data = hmohiv noprint; model time*censor(0)=; baseline out=na cumhaz = h survival=s; run; data na; set na; shat = exp(-h); run; proc print data = na noobs; run;
time s h shat 0 1.00000 0.00000 1.00000 1 0.85000 0.15000 0.86071 2 0.79880 0.21024 0.81039 3 0.68937 0.34723 0.70664 4 0.64417 0.41280 0.66179 5 0.56365 0.53780 0.58403 6 0.54064 0.57862 0.56067 7 0.47012 0.70905 0.49211 8 0.42190 0.81162 0.44414 9 0.38574 0.89733 0.40766 10 0.34958 0.99108 0.37118 11 0.31212 1.09822 0.33346 12 0.28715 1.17822 0.30783 13 0.27348 1.22584 0.29351 14 0.25981 1.27584 0.27920 15 0.23246 1.38111 0.25130 22 0.21793 1.44361 0.23608 30 0.20236 1.51503 0.21980 31 0.18680 1.59196 0.20353 32 0.17123 1.67529 0.18725 34 0.15566 1.76620 0.17098 35 0.14010 1.86620 0.15471 36 0.12453 1.97731 0.13844 43 0.10896 2.10231 0.12217 53 0.09340 2.24517 0.10591 54 0.07783 2.41183 0.08965 57 0.05837 2.66183 0.06982 58 0.03892 2.99517 0.05003
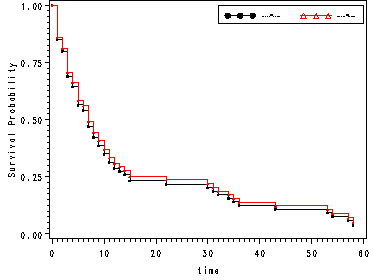
Fig. 2.10, p. 77.
Graphs of the Nelson-Aalen and Kaplan-Meier estimators of the survivorship function from the hmohiv data.
symbol1 value = dot h=.8 i = stepjl color = black;
symbol2 value = triangle h=.8 i = stepjl color = red;
legend1 label=none value=(height=1 font=swiss 'Kaplan-Meier' 'Nelson-Aalen' )
position=(top right inside) mode=share cborder=black;
axis1 label=(a=90 'Survival Probability') order=(0 to 1.0 by .25);
proc gplot data=na;
plot (s shat )*time /overlay legend=legend1 vaxis=axis1;
run;
quit;