Table 2.1 on page 17. We will enter the data for this example.
data ch2f1; input subj time censor; cards; 1 6 1 2 44 1 3 21 0 4 14 1 5 62 1 ; run; proc print data = ch2f1 noobs; run;
subj time censor 1 6 1 2 44 1 3 21 0 4 14 1 5 62 1
Table 2.2, page 20 and Figure 2.1, page 21 using the data we entered above.
proc lifetest data = ch2f1 plot=(s) censoredsymbol=none; time time*censor(0); run;
The LIFETEST Procedure
Product-Limit Survival Estimates
Survival
Standard Number Number
time Survival Failure Error Failed Left
0.0000 1.0000 0 0 0 5
6.0000 0.8000 0.2000 0.1789 1 4
14.0000 0.6000 0.4000 0.2191 2 3
21.0000* . . . 2 2
44.0000 0.3000 0.7000 0.2387 3 1
62.0000 0 1.0000 0 4 0
NOTE: The marked survival times are censored observations.
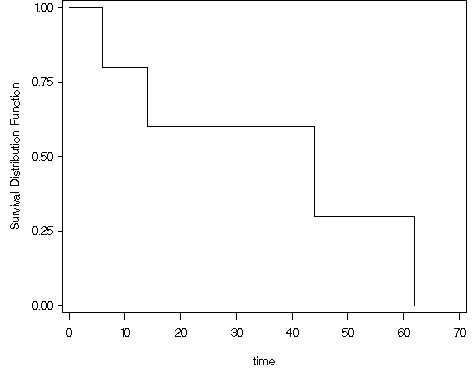
Figure 2.2, page 22 using the whas100 dataset.
data ch2f2; set whas100; year = foltime/365.25; run; proc lifetest data = ch2f2 plot=(s) cs = none; time year*folstatus(0); label year = "Survivial Time (Years)"; run;
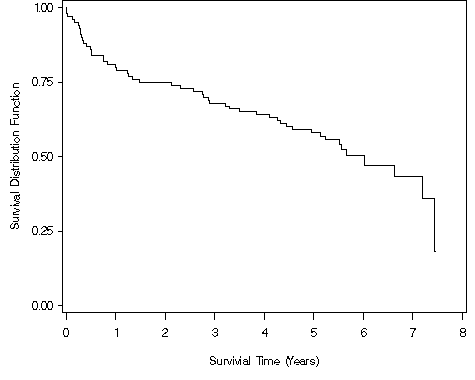
Table 2.3, page 23 using the whas100 dataset as modified in the above example. NOTE: We show two ways of doing this. The first method requires relatively little SAS code, but produces lots of output (some of which we have omitted for space), and does not look like the table presented in the text, although all of the information is in the output. The second method shown below reproduces the table as it appears in the text, but requires considerably more SAS code.
ods select ProductLimitEstimates; proc lifetest data = ch2f2; time foltime*folstatus(0); run;
The LIFETEST Procedure
Product-Limit Survival Estimates
Survival
Standard Number Number
FOLTIME Survival Failure Error Failed Left
0.00 1.0000 0 0 0 100
6.00 . . . 1 99
6.00 0.9800 0.0200 0.0140 2 98
14.00 0.9700 0.0300 0.0171 3 97
44.00 0.9600 0.0400 0.0196 4 96
62.00 0.9500 0.0500 0.0218 5 95
< ... output omitted to save space ... >
2624.00 0.3606 0.6394 0.0857 50 5
2631.00* . . . 50 4
2638.00* . . . 50 3
2641.00* . . . 50 2
2710.00 0.1803 0.8197 0.1345 51 1
2719.00* . . . 51 0
* getting table 2.3, page 23, the hard way; ods listing close; ods output ProductLimitEstimates=d1; proc lifetest data=ch2f2; time foltime*folstatus(0); run; ods listing; data d2; set d1; retain c 0; retain s 1; by foltime; if first.foltime & _n_ >1 then c = censor; else if _n_ > 1 then c = c + censor; if survival ~=. then s = survival; keep foltime failed left c s censor; if last.foltime; run; data d3; set d2; flag = lag(failed); d = failed-flag; llag = lag(left); s1 = (llag -d)/llag; drop flag llag; run; proc print data = d3 (obs = 5); var foltime left d c s1 s; format s1 8.4 s 8.3; run; proc print data = d3 (firstobs = 94 obs=96) noobs; var foltime left d c s1 s; format s1 8.4 s 8.3; run;
FOLTIME Left d c s1 s
0.00 100 . 0 . 1.000
6.00 98 2 0 0.9800 0.980
14.00 97 1 0 0.9898 0.970
44.00 96 1 0 0.9897 0.960
62.00 95 1 0 0.9896 0.950
FOLTIME Left d c s1 s 2641.00 2 0 1 1.0000 0.361 2710.00 1 1 0 0.5000 0.180 2719.00 0 0 1 1.0000 0.180
Table 2.4, page 24 continuing to use the modified whas100 dataset. NOTE: SAS lists a different number of censored observations in the fifth and sixth interval. Hence, the survival estimates are somewhat different from those shown in the text.
proc lifetest data = ch2f2 method = lt; time year*folstatus(0); run;
The LIFETEST Procedure
Life Table Survival Estimates
Conditional
Effective Conditional Probability
Interval Number Number Sample Probability Standard
[Lower, Upper) Failed Censored Size of Failure Error
0 1 20 0 100.0 0.2000 0.0400
1 2 5 0 80.0 0.0625 0.0271
2 3 7 0 75.0 0.0933 0.0336
3 4 4 0 68.0 0.0588 0.0285
4 5 6 0 64.0 0.0938 0.0364
5 6 5 39 38.5 0.1299 0.0542
6 7 2 0 14.0 0.1429 0.0935
7 8 2 10 7.0 0.2857 0.1707
Survival Median Median
Interval Standard Residual Standard
[Lower, Upper) Survival Failure Error Lifetime Error
0 1 1.0000 0 0 6.0648 0.6935
1 2 0.8000 0.2000 0.0400 . .
2 3 0.7500 0.2500 0.0433 . .
3 4 0.6800 0.3200 0.0466 . .
4 5 0.6400 0.3600 0.0480 . .
5 6 0.5800 0.4200 0.0494 . .
6 7 0.5047 0.4953 0.0532 . .
7 8 0.4326 0.5674 0.0656 . .
Figure 2.3, page 25 continuing to use the modified whas100 dataset.
proc lifetest data = ch2f2 intervals=0 to 8 by 1 method = lt outsurv= temp1 maxtime=8;
time year*folstatus(0);
run;
data temp2;
set temp1 end = last;
output;
if last then do;
year = 8;
output;
end;
run;
goptions reset = all;
axis1 label=(a=90 'Estimated Survival Probability') order=(0 to 1 by .2) minor=none ;
axis2 label=('Survival Time (Years)') minor=none order=(0 to 8 by 2) ;
symbol1 i=steplj;
proc gplot data = temp2;
plot survival*year / overlay vaxis=axis1 haxis=axis2;
run;
quit;
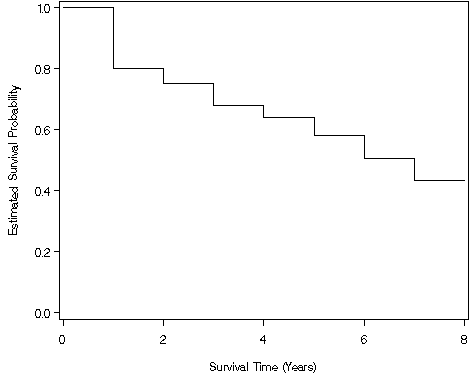
Figure 2.4, page 26 continuing to use the modified whas100 dataset.
proc lifetest data = ch2f2 method = lt plot=(s) cs=none; time year*folstatus(0); run;
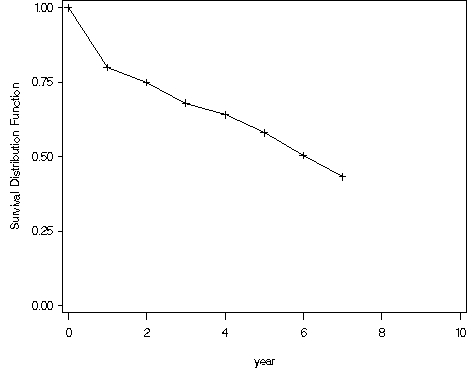
Figure 2.5, page 31 continuing to use the modified whas100 dataset.
proc lifetest data = ch2f2;
time foltime*folstatus(0);
survival out=ch2f5a conftype=loglog confband=hw;
run;
goptions reset = all;
axis1 label=(a=90 'Estimated Survival Probability') order=(0 to 1 by .2) minor=none ;
axis2 label=('Survival Time (Years)') minor=none order=(0 to 2920 by 730)
value=(tick=1 '0' tick=2 '2' tick=3 '4' tick=4 '6' tick=5 '8');
symbol1 i=steplj color=black line=5;
symbol2 i=steplj color=black line=14;
symbol3 i=steplj color=black line=14;
proc gplot data = ch2f5a;
plot (survival sdf_LCL)*foltime / overlay vaxis=axis1 haxis=axis2 legend=legend1;
plot2 sdf_ucl*foltime /overlay vaxis=axis1 noaxis nolegend;
run;
quit;
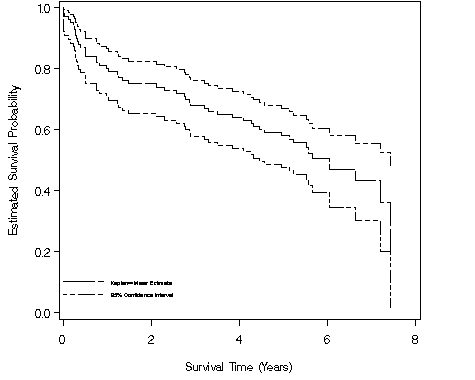
Figure 2.6, page 32 continuing to use the modified whas100 dataset.
proc sort data = ch2f2;
by foltime;
run;
proc lifetest data = ch2f2;
time foltime*folstatus(0);
survival out=ch2f5b conftype=loglog ;
run;
data ch2f5b;
set ch2f5b;
rename SDF_LCL=lcl_loglog SDF_UCL=ucl_loglog;
drop _censor_ CONFTYPE;
run;
proc lifetest data = ch2f2;
time foltime*folstatus(0);
survival out=ch2f5c conftype=log ;
data ch2f5c;
set ch2f5c;
rename SDF_LCL=lcl_log SDF_UCL=ucl_log;
drop _censor_ CONFTYPE;
run;
proc lifetest data = ch2f2;
time foltime*folstatus(0);
survival out=ch2f5d conftype=logit ;
data ch2f5d;
set ch2f5d;
rename SDF_LCL=lcl_logit SDF_UCL=ucl_logit;
drop _censor_ CONFTYPE;
run;
proc lifetest data = ch2f2;
time foltime*folstatus(0);
survival out=ch2f5e conftype=asinsqrt;
run;
data ch2f5e;
set ch2f5e;
rename SDF_LCL=lcl_asinsqrt SDF_UCL=ucl_asinsqrt;
drop _censor_ CONFTYPE;
run;
data ch2f6;
merge ch2f5b ch2f5c ch2f5d ch2f5e;
by foltime;
run;
goptions reset = all;
legend1 label=none value=(h=1.5 font=swiss 'Est. Surv. Pr.' 'Log' 'Log-Log' 'Logit' 'Arcsine'
'lower logit' 'upper logit' 'lower arcsine' 'upper arcsine')
position=(bottom left inside) mode=protect across=2;
axis1 label=(a=90 'Estimated Survival Probability') order=(0 to 1 by .2) minor=none ;
axis2 label=('Survival Time (Years)') minor=none order=(0 to 2920 by 730)
value=(tick=1 '0' tick=2 '2' tick=3 '4' tick=4 '6' tick=5 '8');
symbol1 i=steplj line=1 color=black;
symbol2 i=steplj line=4 color=black;
symbol3 i=steplj line=14 color=black;
symbol4 i=steplj line=46 color=black;
symbol5 i=steplj line=41 color=black;
symbol6 i=steplj line=4 color=black;
symbol7 i=steplj line=14 color=black;
symbol8 i=steplj line=46 color=black;
symbol9 i=steplj line=41 color=black;
proc gplot data = ch2f6;
plot (survival lcl_log lcl_loglog lcl_logit lcl_asinsqrt)*foltime / overlay vaxis=axis1 haxis=axis2 legend=legend1;
plot2 (ucl_log ucl_loglog ucl_logit ucl_asinsqrt)*foltime /overlay vaxis=axis1 noaxis nolegend;
run;
quit;
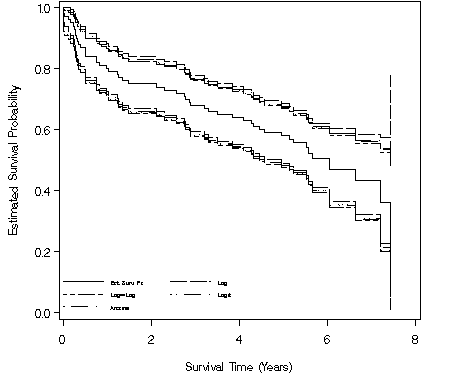
Figure 2.7, page 34 continuing to use the modified whas100 dataset.
proc lifetest data = ch2f2;
time foltime*folstatus(0);
survival out=ch2f5f confband=hw;
run;
goptions reset = all;
legend1 label=none value=(h=1.5 font=swiss 'Est. Surv. Pr.' 'Pointwise 95%' 'Hall & Wellner Band')
position=(bottom center inside) mode=protect down=3 across=1;
axis1 label=(a=90 'Estimated Survival Probability') order=(0 to 1 by .2) minor=none ;
axis2 label=('Survival Time (Years)') minor=none order=(0 to 2920 by 730)
value=(tick=1 '0' tick=2 '2' tick=3 '4' tick=4 '6' tick=5 '8');
symbol1 i=steplj color=black line=1;
symbol2 i=steplj color=black line=14;
symbol3 i=steplj color=black line=46;
symbol4 i=steplj color=black line=14;
symbol5 i=steplj color=black line=46;
proc gplot data = ch2f5f;
plot (survival sdf_ucl hw_ucl)*foltime / overlay vaxis=axis1 haxis=axis2 legend=legend1;
plot2 (sdf_lcl hw_lcl)*foltime /overlay vaxis=axis1 noaxis nolegend;
run;
quit;
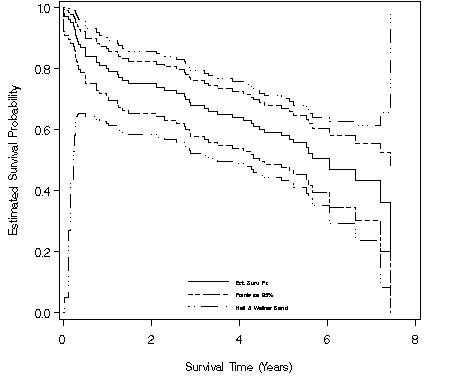
Figure 2.8, page 35 using the dataset entered for Figure 2.1.
goptions reset = all; proc lifetest data = ch2f1 plots=(s) cs=none; time time*censor(0); label time = "Survival Time"; run;
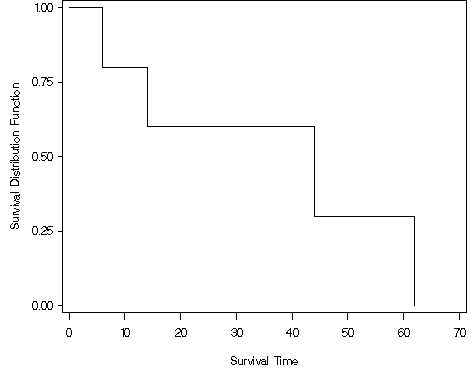
Table 2.5, page 39 using the modified whas100 dataset. NOTE: The SAS output is in a different order than the text. Additionally, SAS computes the 25th percentile as the mean of the event years at at which <=25% and >25% of the subjects have failed (rather that simply last even year where <=25% of the subjects have failed, as is reported in the book) and SAS calculates the confidence intervals differently from the book.
ods select Quartiles; proc lifetest data = ch2f2; time year*folstatus(0); run;
The LIFETEST Procedure
Quartile Estimates
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
75 7.41958 7.18412 .
50 6.02601 4.56947 7.41958
25 1.79603 0.75017 3.49897
Table 2.6, page 41 using the modified whas100 dataset.
proc lifetest data = ch2f2; time year*folstatus(0); survival out=ch2t6 conftype=loglog stderr; run; data ch2t6; set ch2t6; std = sqrt(sdf_stderr**2 /((survival*log(survival))**2)); z50 = abs(log(-log(survival))-log(-log(.5)))/std; run ; proc print data = ch2t6 noobs; var year survival z50 sdf_lcl sdf_ucl; where 4.3 < year < 4.6 or 5.654 < year < 7.6 and sdf_lcl ne .; format year survival sdf_lcl sdf_ucl f8.3; format z50 f8.2; run;
year SURVIVAL z50 SDF_LCL SDF_UCL 4.318 0.610 2.09 0.507 0.698 4.446 0.600 1.91 0.497 0.688 4.569 0.590 1.73 0.487 0.679 6.026 0.469 0.52 0.347 0.582 6.628 0.433 1.04 0.302 0.556 7.184 0.361 1.66 0.200 0.524 7.420 0.180 2.08 0.018 0.482
Table 2.7, page 44 using the dataset entered for Figure 2.1.
proc lifetest data = ch2f1; time time*censor(0); run;
... output omitted to save space ...
Summary Statistics for Time Variable time
Quartile Estimates
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
75 62.0000 14.0000 62.0000
50 44.0000 6.0000 62.0000
25 14.0000 6.0000 62.0000
Mean Standard Error
35.8000 11.8103
data ch2t7; set ch2f1; if subj = 5 then censor = 0; run; proc lifetest data = ch2t7; time time*censor(0); run;
... output omitted to save space ...
Summary Statistics for Time Variable time
Quartile Estimates
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
75 . 14.0000 .
50 44.0000 6.0000 .
25 14.0000 6.0000 .
Mean Standard Error
30.4000 9.2278
NOTE: The mean survival time and its standard error were underestimated because
the largest observation was censored and the estimation was restricted to
the largest event time.
Figure 2.9, page 46 using the modified whas100 dataset.
goptions reset = all; proc lifetest data = ch2f2 plots=(s) cs=none; time foltime*folstatus(0); strata gender; run;
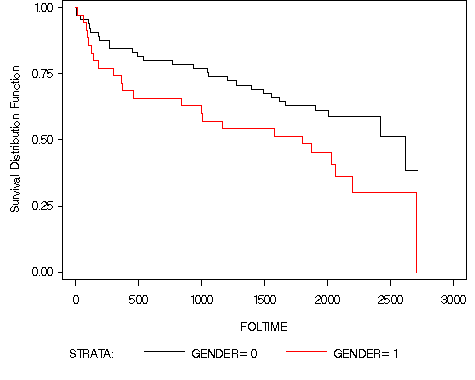
Table 2.10, page 50. We are entering the data for this example.
data ch2t10; input id female time censor fdead fatrisk tdead tatrisk; cards; 1 0 6 1 0 5 1 9 2 0 44 0 . . . . 3 0 98 1 1 2 2 4 4 0 114 1 0 0 1 1 5 1 14 1 1 5 1 8 6 1 44 1 1 4 1 7 7 1 89 0 . . . . 8 1 98 1 1 2 2 4 9 1 104 1 1 1 1 2 ; run; proc sort data = ch2t10; by time; run; data ch2t10a; set ch2t10; retain p 1; n0 = tatrisk - fatrisk; e1 = (fatrisk*tdead)/tatrisk; v1 = (fatrisk*n0*tdead*(tatrisk-tdead))/(tatrisk*tatrisk*(tatrisk-1)); L = 1; t = sqrt(tatrisk); if tatrisk~=. & id~=8 then p = p*(tatrisk+1-tdead)/(tatrisk+1); run; * peto-prentice unmodifed weight is just the survival probability; proc print data = ch2t10a noobs; where censor ne 0 and id ne 8; var time fdead fatrisk tdead tatrisk e1 v1 l tatrisk t p; format e1 v1 t p f8.3; run;
time fdead fatrisk tdead tatrisk e1 v1 L tatrisk t p 6 0 5 1 9 0.556 0.247 1 9 3.000 0.900 14 1 5 1 8 0.625 0.234 1 8 2.828 0.800 44 1 4 1 7 0.571 0.245 1 7 2.646 0.700 98 1 2 2 4 1.000 0.333 1 4 2.000 0.420 104 1 1 1 2 0.500 0.250 1 2 1.414 0.280 114 0 0 1 1 0.000 . 1 1 1.000 0.140
Table 2.11, page 51 using the dataset entered for Table 2.10.
ods select HomTests; proc lifetest data = ch2t10; time time*censor(0); strata female / test=(logrank wilcoxon peto tarone); run;
The LIFETEST Procedure
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 0.4273 1 0.5133
Wilcoxon 0.0750 1 0.7842
Tarone 0.1995 1 0.6551
Peto 0.1050 1 0.7459
Table 2.12, page 51 using the dataset entered for Table 2.10.
ods select HomTests; proc lifetest data = ch2f2; time year*folstatus(0); strata gender / test=(logrank wilcoxon peto tarone); run;
The LIFETEST Procedure
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 3.9714 1 0.0463
Wilcoxon 3.4624 1 0.0628
Tarone 3.6860 1 0.0549
Peto 3.8507 1 0.0497
Table 2.13, page 52 using the whas100 dataset. Note that SAS computes the median as the mean of the event year at which <= 50% of the subjects have failed and the event year at which >50% of the subjects have failed (rather that simply the last event year where <= 50% of the subjects have failed, as is reported in the book).
data ch2t13; set whas100; if (age < 60) then agecat = 1; else if (age < 70) then agecat = 2; else if (age < 80) then agecat = 3; else agecat = 4; year = foltime/365.25; run; proc lifetest data = ch2t13; time year*folstatus(0); strata agecat; run;
< ... output omitted to save space ... >
Stratum 1: agecat = 1
Quartile Estimates
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
75 . . .
50 . 4.31759 .
25 3.83573 2.86927 .
Stratum 2: agecat = 2
Quartile Estimates
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
75 . 7.18412 .
50 7.18412 7.18412 .
25 4.56947 0.49829 .
Stratum 3: agecat = 3
Quartile Estimates
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
75 6.62834 5.22108 .
50 5.08282 2.88569 6.62834
25 0.75017 0.35044 4.94456
Stratum 4: agecat = 4
Quartile Estimates
Point 95% Confidence Interval
Percent Estimate [Lower Upper)
75 6.02601 5.13073 7.41958
50 2.43258 0.99384 5.65366
25 0.40520 0.28474 1.26215
Summary of the Number of Censored and Uncensored Values
Percent
Stratum agecat Total Failed Censored Censored
1 1 25 8 17 68.00
2 2 23 7 16 69.57
3 3 22 14 8 36.36
4 4 30 22 8 26.67
-------------------------------------------------------------------
Total 100 51 49 49.00
Figure 2.10, page 55 using the modified version of whas100 from Table 13.
proc lifetest data = ch2t13 plots=(s) cs=none; time year*folstatus(0); strata agecat / test=(logrank wilcoxon peto tarone); label year = 'Survival Time (Year)'; symbol1 c=black l=1; symbol2 c=black l=4; symbol3 c=black l=14; symbol4 c=black l=22; run;
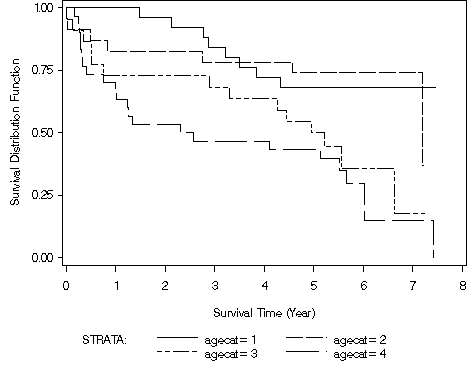
Table 2.15, page 56 using the modified version of whas100 from Table 13.
ods select HomTests; proc lifetest data = ch2t13; time year*folstatus(0); strata agecat / test=(logrank wilcoxon peto tarone); run;
The LIFETEST Procedure
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 15.5721 3 0.0014
Wilcoxon 12.2981 3 0.0064
Tarone 13.5199 3 0.0036
Peto 14.5352 3 0.0023
Table 2.16, page 57 using the modified whas100 from Table 13. NOTE: The text shows a chi-square test and SAS gives a z-test. You can square the z-score from the table below to get the chi-square values shown in the text.
data ch2t16; set ch2t13; if agecat = 1 then agecat1 = 46; if agecat = 2 then agecat1 = 65; if agecat = 3 then agecat1 = 75; if agecat = 4 then agecat1 = 86; run; ods select TrendTests; proc lifetest data = ch2t16; time year*folstatus(0) ; strata agecat1 / test=(logrank wilcoxon peto tarone) trend; run;
Trend Tests
Test Standard
Test Statistic Error z-Score Pr > |z|
Log-Rank 383.5416 108.7485 3.5269 0.0004
Wilcoxon 25474.0000 8060.8167 3.1602 0.0016
Tarone 2969.3761 907.7345 3.2712 0.0011
Peto 283.3549 81.5358 3.4752 0.0005
Figure 2.11, page 58 using the bpd dataset.
proc lifetest data = bpd plots=(s) cs=none; time days*censor(0); strata suf / test=(logrank wilcoxon peto tarone); symbol1 c=black l=1; symbol2 c=black l=4; label days = 'Days on Oxygen'; run;
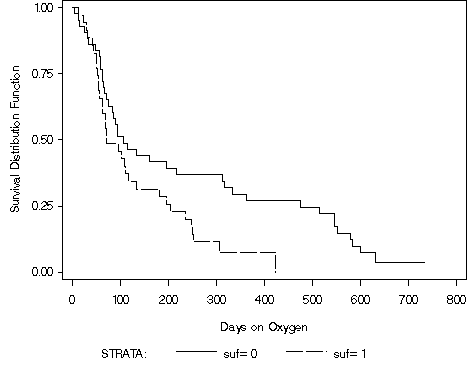
Table 2.17, page 58 using the bpd dataset.
proc lifetest data = bpd; time days*censor(0); strata suf / test=(logrank wilcoxon peto tarone); run;
< ... output omitted to save space ... >
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 5.6180 1 0.0178
Wilcoxon 2.4898 1 0.1146
Tarone 3.6984 1 0.0545
Peto 2.5343 1 0.1114
Figure 2.12, page 61 using the modified version of whas100 from Figure 2.
proc lifetest data = ch2f2;
time foltime*folstatus(0);
survival out=ch2f5a conftype=loglog;
run;
*nelson aalen estimate;
proc phreg data = ch2f2;
model foltime*folstatus(0) = ;
baseline out = ch2f12a survival=sur_nelson lower=low upper=high / method=ch cltype=loglog;
run;
data ch2f12;
merge ch2f5a ch2f12a;
by foltime;
run;
goptions reset = all;
legend1 label=none value=(h=1.5 'Nelson-Aalen' 'N-A Limits' 'Kaplan-Meier' 'K-M Limits')
position=(bottom left inside) mode=protect down=2 across=2;
axis1 label=(a=90 'Estimated Survival Probability') order=(0 to 1 by .2) minor=none ;
axis2 label=('Survival Time (Years)') minor=none order=(0 to 2920 by 730)
value=(tick=1 '0' tick=2 '2' tick=3 '4' tick=4 '6' tick=5 '8');
symbol1 i=steplj color=black line=1;
symbol2 i=steplj color=black line=5;
symbol3 i=steplj color=black line=14;
symbol4 i=steplj color=black line=40;
symbol5 i=steplj color=black line=14;
symbol6 i=steplj color=black line=40;
proc gplot data = ch2f12;
plot (sur_nelson survival high sdf_ucl )*foltime / overlay vaxis=axis1 haxis=axis2 legend=legend1;
plot2 (low sdf_lcl)*foltime /overlay vaxis=axis1 noaxis nolegend;
run;
quit;
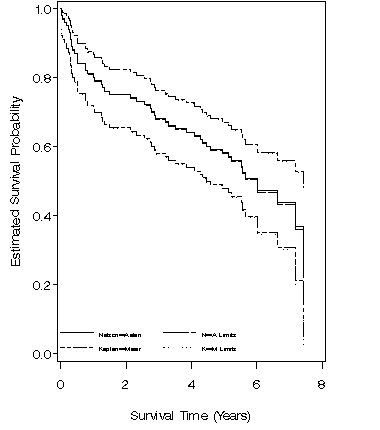
Figure 2.13, page 62 using the modified version of whas100 from Figure 2.
proc phreg data = ch2f2;
model year*folstatus(0) = ;
baseline out = ch2f13 cumhaz=cumhaz;
run;
goptions reset = all;
symbol1 i=steplj color=black line=1;
axis1 label=(a=90 'Nelson-Aalen Estimated Cumulative Hazard Function') order=(0 to 1.5 by .5) minor=none ;
axis2 label=('Survival Time (Years)') minor=none order=(0 to 8 by 2)
value=(tick=1 '0' tick=2 '2' tick=3 '4' tick=4 '6' tick=5 '8');
proc gplot data = ch2f13;
plot cumhaz*year / vaxis=axis1 haxis=axis2;
run;
quit;
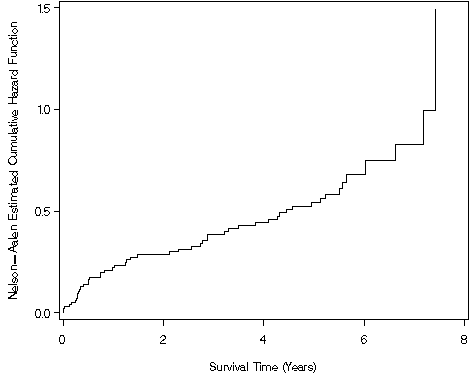
Figure 2.14, page 64
We were unable to reproduce this graph.
