The whas500 data set is used in this chapter. We will also use a macro written to generate Brookmeyer-Crowley confidence intervals (bcconf) and a macro written to perform likelihood ratio tests (lrtest). Please download these two files, read them over, convert them to SAS programs, and create a filename for each. This will allow us to use %include when we wish to invoke the macros. Then run the %include statement before continuing with the examples.
filename bc "C:bcconf.sas"; filename lr "C:lrtest.sas"; %include bc; %include lr;
Table 5.1 on page 142 using the whas500 data and the bcconf macro to obtain the Brookmeyer-Crowley confidence intervals.
NOTE: We use the ods select statement to limit the output to just the part presented in the table.
data t51; set whas500; lf = lenfol / 365.25; run; * gender; ods select CensoredSummary HomTests; proc lifetest data = t51; strata gender / test=(logrank) nodetail; time lf*fstat(0); run;
The LIFETEST Procedure
Summary of the Number of Censored and Uncensored Values
Percent
Stratum GENDER Total Failed Censored Censored
1 0 300 111 189 63.00
2 1 200 104 96 48.00
-------------------------------------------------------------------
Total 500 215 285 57.00
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 7.7911 1 0.0053
%bcconf(t51, lf, fstat, byvar=gender);
Brookmeyer-Crowley 95% Confidence Interval
Lower Upper
GENDER total Estimate Limit Limit bc_lower bc_upper
0 111 5.91781 4.44932 . 4.44932 .
1 104 3.60822 2.47945 4.32603 2.36986 4.32055
* cvd; ods select CensoredSummary HomTests; proc lifetest data = t51; strata cvd / test=(logrank) nodetail; time lf*fstat(0); run;
The LIFETEST Procedure
Summary of the Number of Censored and Uncensored Values
Percent
Stratum CVD Total Failed Censored Censored
1 0 125 45 80 64.00
2 1 375 170 205 54.67
-------------------------------------------------------------------
Total 500 215 285 57.00
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 2.8615 1 0.0907
%bcconf(t51, lf, fstat, byvar=cvd);
Brookmeyer-Crowley 95% Confidence Interval
Lower Upper
CVD total Estimate Limit Limit bc_lower bc_upper
0 45 6.44658 4.31781 6.44658 4.31781 .
1 170 4.32055 3.72329 6.43836 3.72329 5.91781
* afb; ods select CensoredSummary HomTests; proc lifetest data = t51; strata afb / test=(logrank) nodetail; time lf*fstat(0); run;
The LIFETEST Procedure
Summary of the Number of Censored and Uncensored Values
Percent
Stratum AFB Total Failed Censored Censored
1 0 422 168 254 60.19
2 1 78 47 31 39.74
-------------------------------------------------------------------
Total 500 215 285 57.00
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 10.9000 1 0.0010
%bcconf(t51, lf, fstat, byvar=afb);
Brookmeyer-Crowley 95% Confidence Interval
Lower Upper
AFB total Estimate Limit Limit bc_lower bc_upper
0 168 5.91781 4.31781 6.46027 4.31781 6.44658
1 47 2.36986 1.22192 3.77260 1.14795 3.50411
* sho; ods select CensoredSummary HomTests; proc lifetest data = t51; strata sho / test=(logrank) nodetail; time lf*fstat(0); run;
The LIFETEST Procedure
Summary of the Number of Censored and Uncensored Values
Percent
Stratum SHO Total Failed Censored Censored
1 0 478 198 280 58.58
2 1 22 17 5 22.73
-------------------------------------------------------------------
Total 500 215 285 57.00
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 23.8365 1 <.0001
%bcconf(t51, lf, fstat, byvar=sho);
Brookmeyer-Crowley 95% Confidence Interval
Lower Upper
SHO total Estimate Limit Limit bc_lower bc_upper
0 198 5.27671 4.20822 6.46027 4.20822 6.44658
1 17 0.05342 0.01370 1.22192 0.01096 1.14795
* chf; ods select CensoredSummary HomTests; proc lifetest data = t51; strata chf / test=(logrank) nodetail; time lf*fstat(0); run;
The LIFETEST Procedure
Summary of the Number of Censored and Uncensored Values
Percent
Stratum CHF Total Failed Censored Censored
1 0 345 105 240 69.57
2 1 155 110 45 29.03
-------------------------------------------------------------------
Total 500 215 285 57.00
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 84.6007 1 <.0001
%bcconf(t51, lf, fstat, byvar=chf);
Brookmeyer-Crowley 95% Confidence Interval
Lower Upper
CHF total Estimate Limit Limit bc_lower bc_upper
0 105 6.46027 5.91781 6.46027 5.91781 .
1 110 0.98356 0.75068 1.53973 0.70959 1.51233
* av3; ods select CensoredSummary HomTests; proc lifetest data = t51; strata av3 / test=(logrank) nodetail; time lf*fstat(0); run;
The LIFETEST Procedure
Summary of the Number of Censored and Uncensored Values
Percent
Stratum AV3 Total Failed Censored Censored
1 0 489 208 281 57.46
2 1 11 7 4 36.36
-------------------------------------------------------------------
Total 500 215 285 57.00
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 1.5236 1 0.2171
%bcconf(t51, lf, fstat, byvar=av3);
Brookmeyer-Crowley 95% Confidence Interval
Lower Upper
AV3 total Estimate Limit Limit bc_lower bc_upper
0 208 4.45753 4.12603 6.46027 4.12603 6.44658
1 7 5.35342 0.05479 6.43836 0.00548 .
* miord; ods select CensoredSummary HomTests; proc lifetest data = t51; strata miord / test=(logrank) nodetail; time lf*fstat(0); run;
The LIFETEST Procedure
Summary of the Number of Censored and Uncensored Values
Percent
Stratum MIORD Total Failed Censored Censored
1 0 329 125 204 62.01
2 1 171 90 81 47.37
-------------------------------------------------------------------
Total 500 215 285 57.00
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 9.5706 1 0.0020
%bcconf(t51, lf, fstat,byvar= miord);
Brookmeyer-Crowley 95% Confidence Interval
Lower Upper
MIORD total Estimate Limit Limit bc_lower bc_upper
0 125 5.91781 5.27671 6.44658 5.27671 6.43836
1 90 3.37534 1.96712 4.32055 1.96712 4.25479
* mitype; ods select CensoredSummary HomTests; proc lifetest data = t51; strata mitype / test=(logrank) nodetail; time lf*fstat(0); run;
The LIFETEST Procedure
Summary of the Number of Censored and Uncensored Values
Percent
Stratum MITYPE Total Failed Censored Censored
1 0 347 169 178 51.30
2 1 153 46 107 69.93
-------------------------------------------------------------------
Total 500 215 285 57.00
Test of Equality over Strata
Pr >
Test Chi-Square DF Chi-Square
Log-Rank 16.1806 1 <.0001
%bcconf(t51, lf, fstat, byvar=mitype);
Brookmeyer-Crowley 95% Confidence Interval
Lower Upper
MITYPE total Estimate Limit Limit bc_lower bc_upper
0 169 3.50411 2.88767 4.44932 2.61096 4.32603
1 46 6.43836 6.43836 6.44658 . .
Table 5.2 on page 143 using the whas500 data and the lrtest macro which is used to get the p-values in the right-most column of the table.
NOTE: We use the ods select statement to limit the output to just the part presented in the table.
data whas500_t52; set whas500; age5 = age/5; hr10 = hr/10; sysbp10 = sysbp/10; diasbp10 = diasbp/10; bmi5 = bmi/5; run;
* age; ods select ParameterEstimates; proc phreg data = whas500_t52; model lenfol*fstat(0) = age5 / risklimits; run;
The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter Standard
Variable DF Estimate Error Chi-Square Pr > ChiSq
age5 1 0.33123 0.03039 118.7963 <.0001
Analysis of Maximum Likelihood Estimates
Hazard 95% Hazard Ratio
Variable Ratio Confidence Limits
age5 1.393 1.312 1.478
%lrtest(whas500_t52, lenfol, fstat, , age5);
Full model: age5 Test variables: age5 Degrees of freedom: 1 P value: .000
* heart rate; ods select ParameterEstimates; proc phreg data = whas500_t52; model lenfol*fstat(0) = hr10 / risklimits; run;
The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter Standard
Variable DF Estimate Error Chi-Square Pr > ChiSq
hr10 1 0.15036 0.02687 31.3135 <.0001
Analysis of Maximum Likelihood Estimates
Hazard 95% Hazard Ratio
Variable Ratio Confidence Limits
hr10 1.162 1.103 1.225
%lrtest(whas500_t52, lenfol, fstat, , hr10);
Full model: hr10 Test variables: hr10 Degrees of freedom: 1 P value: .000
* sysbp; ods select ParameterEstimates; proc phreg data = whas500_t52; model lenfol*fstat(0) = sysbp10 / risklimits; run;
The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter Standard
Variable DF Estimate Error Chi-Square Pr > ChiSq
sysbp10 1 -0.04502 0.02226 4.0902 0.0431
Analysis of Maximum Likelihood Estimates
Hazard 95% Hazard Ratio
Variable Ratio Confidence Limits
sysbp10 0.956 0.915 0.999
%lrtest(whas500_t52, lenfol, fstat, , sysbp10);
Full model: sysbp10 Test variables: sysbp10 Degrees of freedom: 1 P value: .041
* diasbp; ods select ParameterEstimates; proc phreg data = whas500_t52; model lenfol*fstat(0) = diasbp10 / risklimits; run;
The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter Standard
Variable DF Estimate Error Chi-Square Pr > ChiSq
diasbp10 1 -0.15993 0.03284 23.7145 <.0001
Analysis of Maximum Likelihood Estimates
Hazard 95% Hazard Ratio
Variable Ratio Confidence Limits
diasbp10 0.852 0.799 0.909
%lrtest(whas500_t52, lenfol, fstat, , diasbp10);
Full model: diasbp10 Test variables: diasbp10 Degrees of freedom: 1 P value: .000
* bmi; ods select ParameterEstimates; proc phreg data = whas500_t52; model lenfol*fstat(0) = bmi5 / risklimits; run;
The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter Standard
Variable DF Estimate Error Chi-Square Pr > ChiSq
bmi5 1 -0.49133 0.07372 44.4254 <.0001
Analysis of Maximum Likelihood Estimates
Hazard 95% Hazard Ratio
Variable Ratio Confidence Limits
bmi5 0.612 0.530 0.707
%lrtest(whas500_t52, lenfol, fstat, , bmi5);
Full model: bmi5 Test variables: bmi5 Degrees of freedom: 1 P value: .000
Table 5.3 on page 143 using the whas500 data.
ods output ParameterEstimates=out1;
proc phreg data = whas500;
model lenfol*fstat(0) = age hr sysbp diasbp bmi gender cvd afb chf miord mitype;
run;
data out2;
set out1;
z = estimate /stderr;
lb = estimate-1.96*stderr;
ub = estimate+1.96*stderr;
run;
proc print data = out2 noobs;
var variable estimate stderr z probchisq lb ub;
format z f8.2;
format estimate probchisq lb ub f8.3;
format stderr f8.4;
run;
ProbChi
Variable Estimate StdErr z Sq lb ub
AGE 0.049 0.0068 7.12 0.000 0.035 0.062
HR 0.010 0.0031 3.38 0.001 0.004 0.016
SYSBP 0.000 0.0030 0.12 0.904 -0.006 0.006
DIASBP -0.011 0.0049 -2.16 0.031 -0.020 -0.001
BMI -0.044 0.0164 -2.66 0.008 -0.076 -0.011
GENDER -0.271 0.1457 -1.86 0.063 -0.556 0.015
CVD 0.007 0.1781 0.04 0.967 -0.342 0.356
AFB 0.128 0.1712 0.75 0.455 -0.208 0.464
CHF 0.774 0.1499 5.16 0.000 0.480 1.067
MIORD 0.044 0.1484 0.30 0.768 -0.247 0.335
MITYPE -0.164 0.1879 -0.87 0.382 -0.532 0.204
Table 5.4 on page 144 using the whas500 data.
ods output ParameterEstimates=out3; proc phreg data = whas500; model lenfol*fstat(0) = age hr diasbp bmi gender afb chf miord mitype; run; data out4; set out3; z = estimate /stderr; lb = estimate-1.96*stderr; ub = estimate+1.96*stderr; run; proc print data = out4 noobs; var variable estimate stderr z probchisq lb ub; format z f8.2; format estimate probchisq lb ub f8.3; format stderr f8.4; run;
ProbChi Variable Estimate StdErr z Sq lb ub AGE 0.049 0.0067 7.23 0.000 0.036 0.062 HR 0.010 0.0030 3.45 0.001 0.004 0.016 DIASBP -0.010 0.0035 -2.87 0.004 -0.017 -0.003 BMI -0.044 0.0163 -2.67 0.008 -0.076 -0.012 GENDER -0.268 0.1447 -1.85 0.064 -0.552 0.015 AFB 0.125 0.1697 0.74 0.460 -0.207 0.458 CHF 0.776 0.1486 5.22 0.000 0.485 1.067 MIORD 0.045 0.1454 0.31 0.758 -0.240 0.330 MITYPE -0.169 0.1838 -0.92 0.357 -0.529 0.191
Table 5.5 on page 144 using the whas500 data.
ods output ParameterEstimates=out5; proc phreg data = whas500; model lenfol*fstat(0) = age hr diasbp bmi gender afb chf mitype; run; data out6; set out5; z = estimate /stderr; lb = estimate-1.96*stderr; ub = estimate+1.96*stderr; run; proc print data = out6 noobs; var variable estimate stderr z probchisq lb ub; format z f8.2; format estimate probchisq lb ub f8.3; format stderr f8.4; run;
ProbChi Variable Estimate StdErr z Sq lb ub AGE 0.049 0.0067 7.24 0.000 0.036 0.062 HR 0.010 0.0030 3.49 0.000 0.005 0.016 DIASBP -0.010 0.0035 -2.89 0.004 -0.017 -0.003 BMI -0.044 0.0163 -2.70 0.007 -0.076 -0.012 GENDER -0.274 0.1437 -1.90 0.057 -0.555 0.008 AFB 0.124 0.1697 0.73 0.464 -0.208 0.457 CHF 0.777 0.1486 5.23 0.000 0.486 1.069 MITYPE -0.182 0.1789 -1.02 0.309 -0.533 0.169
Table 5.6 on page 145 using the whas500 data.
ods output ParameterEstimates=out7; proc phreg data = whas500; model lenfol*fstat(0) = age hr diasbp bmi gender chf; run; data out8; set out7; z = estimate /stderr; lb = estimate-1.96*stderr; ub = estimate+1.96*stderr; run; proc print data = out8 noobs; var variable estimate stderr z probchisq lb ub; format z f8.2; format estimate probchisq lb ub f8.3; format stderr f8.4; run;
ProbChi Variable Estimate StdErr z Sq lb ub AGE 0.050 0.0066 7.55 0.000 0.037 0.063 HR 0.011 0.0029 3.83 0.000 0.005 0.017 DIASBP -0.011 0.0035 -3.02 0.003 -0.017 -0.004 BMI -0.045 0.0163 -2.77 0.006 -0.077 -0.013 GENDER -0.270 0.1436 -1.88 0.060 -0.551 0.012 CHF 0.778 0.1467 5.30 0.000 0.490 1.065
Table 5.7 and Figure 5.1 on page 146 using the whas500 data.
We have created a macro for creating this table and the accompanying graph. However, bmi can be treated as a discrete variable or not. Because of this, we have included code so that the output will match exactly with the text.
%macro table5_7(data, des_var, covlist);
proc rank data = &data groups = 4 out = _temp_ ties = low;
var &des_var;
ranks new_&des_var;
run;
proc means data = _temp_ min max;
class new_&des_var;
var &des_var;
ods output Summary = _temp_cut;
run;
data _temp_a;
set _temp_;
&des_var.cat1 = (new_&des_var=1);
&des_var.cat2 = (new_&des_var=2);
&des_var.cat3 = (new_&des_var=3);
run;
proc phreg data = _temp_a;
model lenfol*fstat(0) = &des_var.cat1 &des_var.cat2 &des_var.cat3 &covlist;
ods output ParameterEstimates = _temp_parm;
run;
data _temp_parma (keep = new_&des_var p);
set _temp_parm;
if _n_=1 then do;
new_&des_var = 0;
p = 0;
output;
new_&des_var = 1;
p = estimate;
output;
end;
if _n_=2 then do;
new_&des_var = 2;
p = estimate;
output;
end;
if _n_=3 then do;
new_&des_var = 3;
p = estimate;
output;
end;
if _n_<=3;
run;
data _temp_graph;
merge _temp_cut _temp_parma;
by new_&des_var;
x = (&des_var._min + &des_var._max)/2;
run;
proc print data = _temp_graph noobs label;
var x p;
format p f8.3;
format x f8.1;
label x="&des_var Quartile Midpoint" p='Coeff.';
run;
symbol i = join v = dot;
axis1 label=(a=90 'Estimated Log Hazard') minor=none;
axis2 label=("&des_var");
title "Estimated Coefficients for &des_var Quartiles";
proc gplot data = _temp_graph;
plot p*x / vaxis=axis1 haxis=axis2;
run;
quit;
title;
%mend;
%table5_7(whas500, age, hr diasbp bmi gender chf);
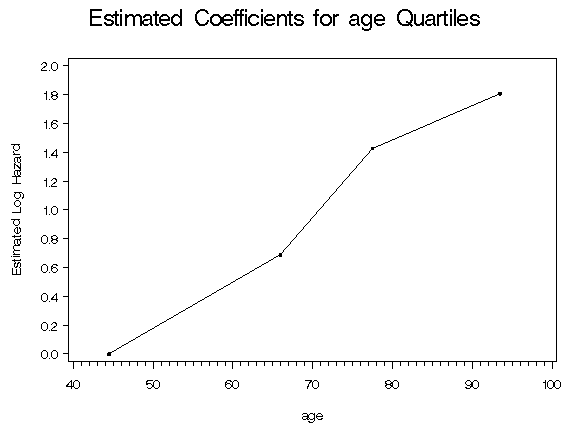
age
Quartile
Midpoint Coeff.
44.5 0.000
66.0 0.690
77.5 1.428
93.5 1.807
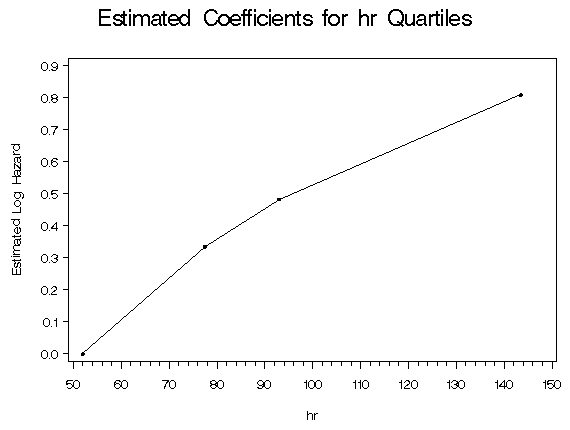
%table5_7(whas500, hr, age diasbp bmi gender chf);
hr
Quartile
Midpoint Coeff.
52.0 0.000
77.5 0.335
93.0 0.483
143.5 0.809
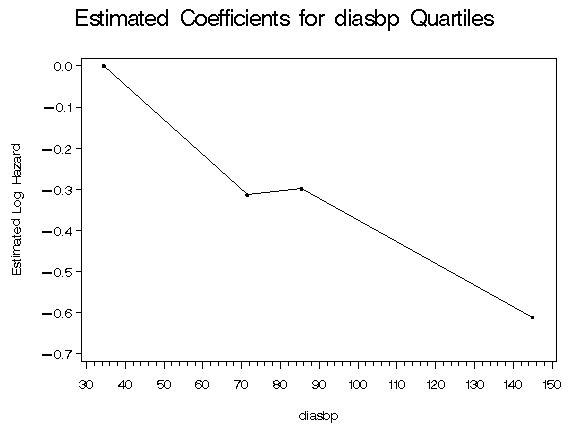
%table5_7(whas500, diasbp, age hr bmi gender chf);
diasbp
Quartile
Midpoint Coeff.
34.5 0.000
71.5 -0.314
85.5 -0.298
145.0 -0.610
%table5_7(whas500, bmi, age hr diasbp gender chf);
bmi
Quartile
Midpoint Coeff.
18.1 0.000
24.6 -0.403
27.7 -0.370
37.1 -0.430
* code to make bmi match to text;
data part4b; set whas500; bmicat0 = (bmi le 23); bmicat1 = (23 < bmi <= 26); bmicat2 = (26< bmi <= 29); bmicat3 = (bmi gt 29); if bmicat0 = 1 then nbmi = 0; if bmicat1 = 1 then nbmi = 1; if bmicat2 = 1 then nbmi = 2; if bmicat3 = 1 then nbmi = 3; run; proc freq data = part4b; tables nbmi; tables bmicat0 bmicat1 bmicat2 bmicat3; run; proc phreg data = part4b; model lenfol*fstat(0) = bmicat1 bmicat2 bmicat3 age hr diasbp gender chf; ods output ParameterEstimates = part4_parm; run; proc univariate data = whas500; var bmi; output out = part4_sum min=min q1=q1 median=median q3=q3 max=max; run; data part4_cut; set part4_sum; new_bmi = 0; x = (min+q1)/2; output; new_bmi = 1; x = (q1 + median)/2; output; new_bmi = 2; x = (median + q3)/2; output; new_bmi = 3; x = (q3+max)/2; output; keep new_bmi x; run; data part4_parma (keep = new_bmi p); set part4_parm; if _n_=1 then do; new_bmi = 0; p = 0; output; new_bmi = 1; p = estimate; output; end; if _n_=2 then do; new_bmi = 2; p = estimate; output; end; if _n_=3 then do; new_bmi = 3; p = estimate; output; end; if _n_<=3; run; data part4_graph; merge part4_cut part4_parma; by new_bmi; x = put(x, 8.1); run; proc print data = part4_graph noobs label; var x p; format p f8.3; label x="BMI Quartile Midpoint" p='Coeff.'; run;
BMI
Quartile
Midpoint Coeff.
18.1 0.000
24.6 -0.453
27.7 -0.315
37.1 -0.592
goptions reset=all;
symbol i = join v = dot;
axis1 order=(-.6 to 0 by .2) label=(a=90 'Estimated Log Hazard') minor=none;
axis2 order=(18.1 24.6 27.7 37.1) label=('Body Mass Index (kg/m^2)');
title 'Estimated Coefficients for Body Mass Index Quartiles';
proc gplot data = part4_graph;
plot p*x / vaxis = axis1 haxis = axis2;
run;
quit;
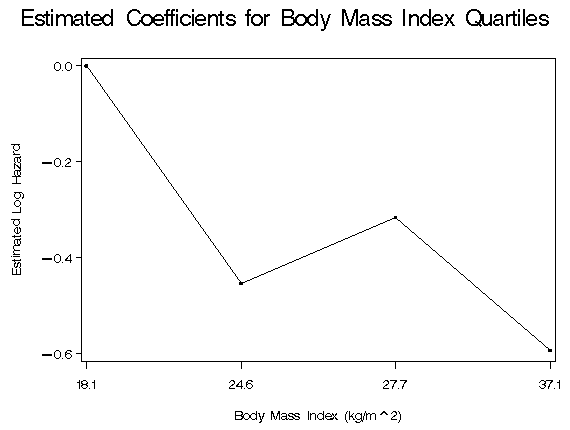
Table 5.8 on page 147 using the whas500 data. For each fitted model, we use the ods output statement to save the fit statistics as a dataset. These datasets are then combined and compared using a likelihood ratio tests.
data table58;
set whas500;
bmi12 = bmi**(-2);
bmi2 = (bmi/10)**2;
bmi3 = (bmi/10)**3;
run;
* not in the model;
ods output FitStatistics = not;
proc phreg data = whas500;
model lenfol*fstat(0) = age hr diasbp gender chf;
run;
* linear;
ods output FitStatistics = linear;
proc phreg data = whas500;
model lenfol*fstat(0) = age hr diasbp bmi gender chf;
run;
* j = 1 (2 df);
ods output FitStatistics = j1;
proc phreg data = table58;
model lenfol*fstat(0) = age hr diasbp bmi12 gender chf;
run;
* j = 2 (4 df);
ods output FitStatistics = j2;
proc phreg data = table58;
model lenfol*fstat(0) = age hr diasbp bmi2 bmi3 gender chf;
run;
data _null_;
set not;
if _n_ = 1 then call symput('not', withcovariates);
set linear;
if _n_ = 1 then call symput('linear', withcovariates);
set j1;
if _n_ = 1 then call symput('j1', withcovariates);
set j2;
if _n_ = 1 then call symput('j2', withcovariates);
run;
data table5_8;
length power $8;
loglikelihood = ¬
gstat = .;
pvalue = .;
power = "";
output;
loglikelihood = &linear;
gstat = &linear-&linear;
pvalue = 1- probchi(¬ - &linear ,1);
power = "1";
output;
loglikelihood = &j1;
gstat = &linear - &j1;
pvalue = 1- probchi(&linear - &j1 ,1);
power = "-2";
output;
loglikelihood = &j2;
gstat = &linear - &j2;
pvalue = 1- probchi(&j1 - &j2 ,2);
power = "(2,3)";
output;
run;
proc print data = table5_8 noobs;
var loglikelihood gstat pvalue power;
format loglikelihood gstat pvalue f8.3;
run;
loglikelihood gstat pvalue power 2255.945 . . 2247.999 0.000 0.005 1 2241.668 6.331 0.012 -2 2237.784 10.215 0.143 (2,3)
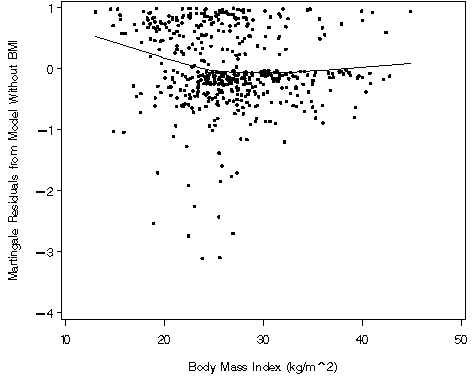
Figure 5.2 on page 149 using the whas500 data.
proc phreg data = whas500;
model lenfol*fstat(0) = age hr diasbp gender chf;
id id;
output out=fig52ar resmart=mart;
run;
proc sort data = whas500;
by id;
run;
proc sort data = fig52ar;
by id;
run;
data fig52a;
merge fig52ar whas500;
by id;
run;
proc loess data = fig52a;
model mart = bmi ;
ods output OutputStatistics=results_fig52a;
run;
proc sort data=results_fig52a;
by bmi;
run;
goptions reset=all;
axis1 order=(-4 to 1 by 1) label=(a=90 'Martingale Residuals from Model Without BMI') minor=none;
axis2 order=(10 to 50 by 10) label=('Body Mass Index (kg/m^2)') minor=none;
symbol1 v=dot i=none c=black;
symbol2 v=none i=join c=black;
proc gplot data = results_fig52a;
plot DepVar*bmi=1 pred*bmi=2 / overlay vaxis = axis1 haxis = axis2;
run;
quit;
proc phreg data = whas500;
model lenfol*fstat(0) = age hr diasbp gender chf bmi;
id id;
output out=fig52br resmart=mart_full;
run;
data temp1;
set fig52br;
hat = fstat - mart_full;
run;
proc loess data = temp1;
model fstat = bmi / smooth = .4 bucket = 20;
ods output OutputStatistics=results_fig52b1;
run;
data temp2;
set results_fig52b1;
rename DepVar = depvar_fstat;
rename Pred = pred_fstat;
run;
proc loess data = temp1;
model hat = bmi / smooth = .4 bucket = 20;
ods output OutputStatistics=results_fig52b2;
run;
data temp3;
set results_fig52b2;
rename DepVar = depvar_hat;
rename Pred = pred_hat;
run;
proc sort data = temp2;
by obs;
run;
proc sort data = temp3;
by obs;
run;
data temp4;
merge temp2 temp3;
by obs;
run;
data temp5;
set temp4;
f = log(pred_fstat/pred_hat)-.0451558*bmi;
id = obs;
run;
proc sort data = temp5;
by bmi;
run;
goptions reset=all;
axis1 order=(-1.5 to .5 by .5) label=(a=90 'ln(csmoothed/Hsmoothed)+beta*x') minor=none;
axis2 order=(10 to 50 by 10) label=('Body Mass Index (kg/m^2)') minor=none;
symbol1 v=none i=join c=black;
proc gplot data = temp5;
plot f*bmi / vaxis = axis1 haxis = axis2;
run;
quit;
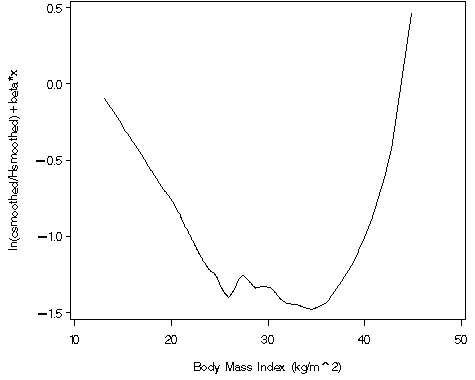
Table 5.9 on page 150 using the modified version of the whas500 data from Table 5.8.
proc phreg data = table58; model lenfol*fstat(0) = bmi2 bmi3 age hr diasbp gender chf; run;
< some output omitted >
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
bmi2 1 -0.72476 0.17261 17.6297 <.0001 0.484
bmi3 1 0.15442 0.03923 15.4958 <.0001 1.167
AGE 1 0.04978 0.00661 56.6729 <.0001 1.051
HR 1 0.01180 0.00295 15.9574 <.0001 1.012
DIASBP 1 -0.01067 0.00350 9.2930 0.0023 0.989
GENDER 1 -0.32640 0.14422 5.1226 0.0236 0.722
CHF 1 0.82341 0.14718 31.3003 <.0001 2.278
Figure 5.3 on page 150 using the whas500 data and the data generated in the previous example from the two term model.
data temp6;
set whas500;
bmifp1=(bmi/10)**2;
bmifp2=(bmi/10)**3;
run;
proc sort data = temp5;
by id;
run;
proc means data = temp6;
var id;
run;
proc sort data = temp6;
by id;
run;
data temp7;
merge temp5 temp6;
by id;
run;
proc phreg data = whas500;
model lenfol*fstat(0) = bmifp1 bmifp2 age hr diasbp gender chf;
run;
* f is generated in the temp5 data set above;
data temp8;
set temp7;
fp_funct=-0.72476*bmifp1+0.15442*bmifp2;
diff=f-fp_funct;
run;
data temp8;
set temp7;
fp_funct=-0.725*bmifp1+0.154*bmifp2;
diff=f-fp_funct;
run;
proc means data = temp8;
var diff;
run;
data temp9;
set temp8;
fp_funct1 = fp_funct + 0.9076111;
run;
proc sort data = temp9;
by bmi;
run;
proc means data = temp9;
var bmi f fp_funct1;
run;
goptions reset=all;
axis1 order=(-1.5 to .5 by .5) label=(a=90 'Estimated Log Hazard') minor=none;
axis2 order=(10 to 50 by 10) label=('Body Mass Index (kg/m^2)') minor=none;
symbol1 v=none i=join c=red line=1;
symbol2 v=none i=join c=black line=14;
legend label=none value=('GTF Smooth' 'Two Term (2, 3) Model')
position=(top left inside) mode=share down = 2;
proc gplot data = temp9;
plot fp_funct1*bmi=1 f*bmi=2 / vaxis = axis1 haxis = axis2 overlay legend = legend;
run;
quit;
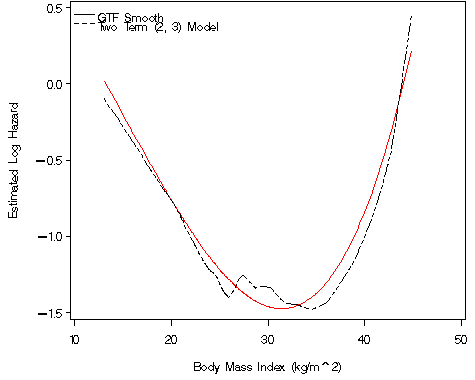
Table 5.10 on page 151 using the whas500 data and the lrtest macro.
data table510; set whas500; bmi2=(bmi/10)**2; bmi3=(bmi/10)**3; /* Creating age interactions */ bmi2age=age*(bmi/10)**2; bmi3age=age*(bmi/10)**3; hrage=age*hr; diasbpage=age*diasbp; genderage=age*gender; chfage=age*chf; /* Creating gender interactions */ bmi2gender=gender*(bmi/10)**2; bmi3gender=gender*(bmi/10)**3; hrgender=gender*hr; diasbpgender=gender*diasbp; chfgender=gender*chf; run; /* With Age Interactions */ %lrtest(table510, lenfol, fstat, bmi2 bmi3 age hr diasbp gender chf, bmi2age bmi3age);
Full model: bmi2 bmi3 age hr diasbp gender chf bmi2age bmi3age Reduced model: bmi2 bmi3 age hr diasbp gender chf Test variables: bmi2age bmi3age Degrees of freedom: 2 P value: .190
%lrtest(table510, lenfol, fstat, bmi2 bmi3 age hr diasbp gender chf, hrage);
Full model: bmi2 bmi3 age hr diasbp gender chf hrage Reduced model: bmi2 bmi3 age hr diasbp gender chf Test variables: hrage Degrees of freedom: 1 P value: .132
%lrtest(table510, lenfol, fstat, bmi2 bmi3 age hr diasbp gender chf, diasbpage);
Full model: bmi2 bmi3 age hr diasbp gender chf diasbpage Reduced model: bmi2 bmi3 age hr diasbp gender chf Test variables: diasbpage Degrees of freedom: 1 P value: .100
%lrtest(table510, lenfol, fstat, bmi2 bmi3 age hr diasbp gender chf, genderage);
Full model: bmi2 bmi3 age hr diasbp gender chf genderage Reduced model: bmi2 bmi3 age hr diasbp gender chf Test variables: genderage Degrees of freedom: 1 P value: .022
%lrtest(table510, lenfol, fstat, bmi2 bmi3 age hr diasbp gender chf, chfage);
Full model: bmi2 bmi3 age hr diasbp gender chf chfage Reduced model: bmi2 bmi3 age hr diasbp gender chf Test variables: chfage Degrees of freedom: 1 P value: .025 /* With Gender Interactions */ %lrtest(table510, lenfol, fstat, bmi2 bmi3 age hr diasbp gender chf, bmi2gender bmi3gender);
Full model: bmi2 bmi3 age hr diasbp gender chf bmi2gender bmi3gender Reduced model: bmi2 bmi3 age hr diasbp gender chf Test variables: bmi2gender bmi3gender Degrees of freedom: 2 P value: .147
%lrtest(table510, lenfol, fstat, bmi2 bmi3 age hr diasbp gender chf, hrgender);
Full model: bmi2 bmi3 age hr diasbp gender chf hrgender Reduced model: bmi2 bmi3 age hr diasbp gender chf Test variables: hrgender Degrees of freedom: 1 P value: .145
%lrtest(table510, lenfol, fstat, bmi2 bmi3 age hr diasbp gender chf, diasbpgender);
Full model: bmi2 bmi3 age hr diasbp gender chf diasbpgender Reduced model: bmi2 bmi3 age hr diasbp gender chf Test variables: diasbpgender Degrees of freedom: 1 P value: .080
%lrtest(table510, lenfol, fstat, bmi2 bmi3 age hr diasbp gender chf, chfgender);
Full model: bmi2 bmi3 age hr diasbp gender chf chfgender Reduced model: bmi2 bmi3 age hr diasbp gender chf Test variables: chfgender Degrees of freedom: 1 P value: .482
Tables 5.11, 5.12, and 5.13 on pages 152 and 153 using the whas500 data as modified for Table 5.8.
/* 5.11 */ proc phreg data = table58; model lenfol*fstat(0) = bmi2 bmi3 age hr diasbp gender chf agegender; agegender = age*gender; run;
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
bmi2 1 -0.67309 0.17358 15.0363 0.0001 0.510
bmi3 1 0.14214 0.03944 12.9886 0.0003 1.153
AGE 1 0.06053 0.00832 52.9614 <.0001 1.062
HR 1 0.01167 0.00294 15.7310 <.0001 1.012
DIASBP 1 -0.01071 0.00347 9.5085 0.0020 0.989
GENDER 1 1.85462 0.95783 3.7492 0.0528 6.389
CHF 1 0.82352 0.14654 31.5808 <.0001 2.279
agegender 1 -0.02766 0.01205 5.2685 0.0217 0.973
/* 5.12 */
proc phreg data = table58;
model lenfol*fstat(0) = bmi2 bmi3 age hr diasbp gender chf agegender agechf agediasbp genderdiasbp;
agegender = age*gender;
agechf = age*chf;
agediasbp = age*diasbp;
genderdiasbp = gender*diasbp;
run;
The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
bmi2 1 -0.64101 0.17539 13.3582 0.0003 0.527
bmi3 1 0.13723 0.04000 11.7676 0.0006 1.147
AGE 1 0.03382 0.02032 2.7699 0.0961 1.034
HR 1 0.01119 0.00297 14.1921 0.0002 1.011
DIASBP 1 -0.05269 0.02130 6.1199 0.0134 0.949
GENDER 1 0.74765 1.22006 0.3755 0.5400 2.112
CHF 1 2.45613 1.00301 5.9964 0.0143 11.660
agegender 1 -0.02202 0.01316 2.7986 0.0943 0.978
agechf 1 -0.02029 0.01272 2.5466 0.1105 0.980
agediasbp 1 0.0004846 0.0002649 3.3464 0.0674 1.000
genderdiasbp 1 0.00899 0.00693 1.6823 0.1946 1.009
/* 5.13 */
proc phreg data = table58;
model lenfol*fstat(0) = bmi2 bmi3 age hr diasbp gender chf agegender;
agegender = age*gender;
run;
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
bmi2 1 -0.67309 0.17358 15.0363 0.0001 0.510
bmi3 1 0.14214 0.03944 12.9886 0.0003 1.153
AGE 1 0.06053 0.00832 52.9614 <.0001 1.062
HR 1 0.01167 0.00294 15.7310 <.0001 1.012
DIASBP 1 -0.01071 0.00347 9.5085 0.0020 0.989
GENDER 1 1.85462 0.95783 3.7492 0.0528 6.389
CHF 1 0.82352 0.14654 31.5808 <.0001 2.279
agegender 1 -0.02766 0.01205 5.2685 0.0217 0.973
Table 5.14 on page 158 using the whas500 data as modified for Table 5.8. For each step, we have formatted in bold the statistics shown in the text.
proc phreg data = table58; model lenfol*fstat(0) = age chf hr diasbp bmi gender mitype miord sysbp cvd afb / selection = forward details slentry = 0.25 sls = 0.8; run;
The PHREG Procedure
Model Information
Data Set WORK.TABLE58
Dependent Variable LENFOL
Censoring Variable FSTAT
Censoring Value(s) 0
Ties Handling BRESLOW
Number of Observations Read 500
Number of Observations Used 500
Summary of the Number of Event and Censored Values
Percent
Total Event Censored Censored
500 215 285 57.00
Analysis of Variables Not in the Model
Score
Variable Chi-Square Pr > ChiSq
AGE 126.2605 <.0001
CHF 84.3701 <.0001
HR 31.2839 <.0001
DIASBP 23.3804 <.0001
BMI 44.1654 <.0001
GENDER 7.7720 0.0053
MITYPE 16.1432 <.0001
MIORD 9.5467 0.0020
SYSBP 4.0922 0.0431
CVD 2.8547 0.0911
AFB 10.8722 0.0010
Step 1. Variable AGE is entered. The model contains the following explanatory
variables:
AGE
< some output omitted >
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
AGE 1 0.06625 0.00608 118.7963 <.0001 1.068
Analysis of Variables Not in the Model
Score
Variable Chi-Square Pr > ChiSq
CHF 38.4054 <.0001
HR 19.0853 <.0001
DIASBP 5.7844 0.0162
BMI 7.2246 0.0072
GENDER 0.2175 0.6409
MITYPE 2.6101 0.1062
MIORD 1.8527 0.1735
SYSBP 3.8985 0.0483
CVD 0.0254 0.8733
AFB 4.1289 0.0422
Step 2. Variable CHF is entered. The model contains the following explanatory
variables:
AGE CHF
< some output omitted >
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
AGE 1 0.05860 0.00610 92.4062 <.0001 1.060
CHF 1 0.86085 0.14235 36.5698 <.0001 2.365
Analysis of Variables Not in the Model
Score
Variable Chi-Square Pr > ChiSq
HR 9.1084 0.0025
DIASBP 5.4058 0.0201
BMI 8.2188 0.0041
GENDER 1.2019 0.2729
MITYPE 2.9333 0.0868
MIORD 1.8879 0.1694
SYSBP 4.4567 0.0348
CVD 0.1742 0.6764
AFB 1.0596 0.3033
Step 3. Variable HR is entered. The model contains the following explanatory
variables:
AGE CHF HR
< some output omitted >
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
AGE 1 0.05905 0.00617 91.6434 <.0001 1.061
CHF 1 0.75665 0.14589 26.8996 <.0001 2.131
HR 1 0.00867 0.00287 9.1191 0.0025 1.009
Analysis of Variables Not in the Model
Score
Variable Chi-Square Pr > ChiSq
DIASBP 9.2900 0.0023
BMI 8.3197 0.0039
GENDER 1.8804 0.1703
MITYPE 1.6807 0.1948
MIORD 1.1879 0.2758
SYSBP 4.7888 0.0286
CVD 0.1367 0.7116
AFB 0.6020 0.4378
Step 4. Variable DIASBP is entered. The model contains the following
explanatory variables:
AGE CHF HR DIASBP
< some output omitted >
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
AGE 1 0.05359 0.00631 72.0525 <.0001 1.055
CHF 1 0.74062 0.14622 25.6536 <.0001 2.097
HR 1 0.01075 0.00294 13.4105 0.0003 1.011
DIASBP 1 -0.01079 0.00353 9.3578 0.0022 0.989
Analysis of Variables Not in the Model
Score
Variable Chi-Square Pr > ChiSq
BMI 7.1659 0.0074
GENDER 2.9642 0.0851
MITYPE 0.8518 0.3561
MIORD 0.7155 0.3976
SYSBP 0.0058 0.9395
CVD 0.0027 0.9582
AFB 0.9543 0.3286
Step 5. Variable BMI is entered. The model contains the following explanatory
variables:
AGE CHF HR DIASBP BMI
< some output omitted >
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
AGE 1 0.04805 0.00656 53.6544 <.0001 1.049
CHF 1 0.74520 0.14583 26.1132 <.0001 2.107
HR 1 0.01070 0.00293 13.3047 0.0003 1.011
DIASBP 1 -0.01019 0.00355 8.2368 0.0041 0.990
BMI 1 -0.04271 0.01595 7.1716 0.0074 0.958
Analysis of Variables Not in the Model
Score
Variable Chi-Square Pr > ChiSq
GENDER 3.5509 0.0595
MITYPE 0.8205 0.3650
MIORD 0.4975 0.4806
SYSBP 0.0003 0.9851
CVD 0.0539 0.8164
AFB 0.5165 0.4723
Step 6. Variable GENDER is entered. The model contains the following
explanatory variables:
AGE CHF HR DIASBP BMI GENDER
< some output omitted >
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
AGE 1 0.04979 0.00660 56.9804 <.0001 1.051
CHF 1 0.77764 0.14670 28.1009 <.0001 2.176
HR 1 0.01118 0.00292 14.7008 0.0001 1.011
DIASBP 1 -0.01059 0.00351 9.0927 0.0026 0.989
BMI 1 -0.04516 0.01628 7.6981 0.0055 0.956
GENDER 1 -0.26999 0.14362 3.5341 0.0601 0.763
Analysis of Variables Not in the Model
Score
Variable Chi-Square Pr > ChiSq
MITYPE 0.9514 0.3294
MIORD 0.2701 0.6033
SYSBP 0.0490 0.8247
CVD 0.0781 0.7799
AFB 0.4458 0.5043
Summary of Forward Selection
Variable Number Score
Step Entered In Chi-Square Pr > ChiSq
1 AGE 1 126.2605 <.0001
2 CHF 2 38.4054 <.0001
3 HR 3 9.1084 0.0025
4 DIASBP 4 9.2900 0.0023
5 BMI 5 7.1659 0.0074
6 GENDER 6 3.5509 0.0595
Table 5.15 on page 161 using the whas500 data as modified for Table 5.8.
NOTE: Lines 3 and 4 are reversed from what is shown in the text.
proc phreg data = table58;
model lenfol*fstat(0) = age chf hr diasbp bmi gender mitype miord sysbp cvd afb
/ selection=score best=3;
ods output BestSubsets = bestsub;
run;
* last is 0/1 temporary variable;
data _null_;
set bestsub end=last;
if last then call symput('s11', scorechisq);
run;
data bestsub_a;
set bestsub;
sq = &s11 - scorechisq;
c = sq - (11 - 2*numberinmodel);
run;
proc sort data = bestsub_a;
by c;
run;
proc print data = bestsub_a (obs = 5) noobs label;
var VariablesInModel c sq;
format c sq f8.2;
label VariablesInModel = "Model Covariates";
run;
Model Covariates c sq AGE CHF HR DIASBP BMI GENDER 3.13 2.13 AGE CHF HR DIASBP BMI GENDER MITYPE 3.58 0.58 AGE CHF HR DIASBP BMI GENDER SYSBP 4.77 1.77 AGE CHF HR DIASBP BMI 4.95 5.95 AGE CHF HR DIASBP BMI GENDER MIORD 4.99 1.99
We were unable to reproduce table 5.16 on page 165.
Table 5.17, page 166 and table 5.18, page 167 are not reproduced because they use hypothetical data.
