Page 283 The coefficients at the top of the page.
data depress; set "c:\cama4\depress"; run; proc logistic data = depress desc; model cases = age income; run;
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 0.0280 0.4872 0.0033 0.9542
AGE 1 -0.0202 0.00890 5.1385 0.0234
INCOME 1 -0.0413 0.0141 8.6500 0.0033
<some output omitted>
Page 283 Figure 12.1 Logistic function for the depression data set.
NOTE: We were unable to reproduce this graph.
Page 285 Table 12.1 Classification of individuals by depression level and sex.
proc freq data = depress; tables sex*cases; run;
The FREQ Procedure
Table of SEX by CASES
SEX CASES
Frequency|
Percent |
Row Pct |
Col Pct | 0| 1| Total
---------+--------+--------+
1 | 101 | 10 | 111
| 34.35 | 3.40 | 37.76
| 90.99 | 9.01 |
| 41.39 | 20.00 |
---------+--------+--------+
2 | 143 | 40 | 183
| 48.64 | 13.61 | 62.24
| 78.14 | 21.86 |
| 58.61 | 80.00 |
---------+--------+--------+
Total 244 50 294
82.99 17.01 100.00
Page 286 Odds ratios and coefficients
data depress; set depress; sex1 = sex - 1; run; proc logistic data = depress desc; model cases = sex1; run;
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -2.3125 0.3315 48.6603 <.0001
sex1 1 1.0385 0.3767 7.6013 0.0058
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
sex1 2.825 1.350 5.911
<some output omitted>
Page 287 Table of coefficients and standard errors.
proc logistic data = depress desc; model cases = age income; run;
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 0.0280 0.4872 0.0033 0.9542 age 1 -0.0202 0.00890 5.1385 0.0234 income 1 -0.0413 0.0141 8.6500 0.0033
Odds Ratio Estimates
Point 95% Wald Effect Estimate Confidence Limits
age 0.980 0.963 0.997 income 0.959 0.933 0.986 <some output omitted>
Page 288 These numbers are obtained from the output from page 287.
Page 290 Table at the top of the page
NOTE: We will create the interaction of the two dummy variables (which we called dincemp) in this data step for use in the example on page 291.
data depress; set depress; if income >= 10 then duminc = 0; else duminc = 1; if employ = 2 or employ = 3 then dumemp = 1; else dumemp = 0; if employ = 7 then dumemp = .; dincemp = duminc*dumemp; run;
proc logistic data = depress desc; model cases = duminc dumemp; run; quit;
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.9345 0.2259 73.3313 <.0001 duminc 1 0.2723 0.3377 0.6502 0.4200 dumemp 1 1.0285 0.3487 8.6990 0.0032
Odds Ratio Estimates
Point 95% Wald Effect Estimate Confidence Limits
duminc 1.313 0.677 2.545 dumemp 2.797 1.412 5.540 <some output omitted>
Page 291 Table in the middle of the page
proc logistic data = depress desc; model cases = duminc dumemp dincemp; run; quit;
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 16.8347 3 0.0008 Score 22.4086 3 <.0001 Wald 16.8136 3 0.0008
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 8.6045 2 0.0135 Score 9.5814 2 0.0083 Wald 9.0619 2 0.0108
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.7346 0.2214 61.3804 <.0001 duminc 1 -0.3756 0.4349 0.7458 0.3878 dumemp 1 0.3175 0.4520 0.4935 0.4824 dincemp 1 2.1981 0.7888 7.7651 0.0053
Odds Ratio Estimates
Point 95% Wald Effect Estimate Confidence Limits
duminc 0.687 0.293 1.611 dumemp 1.374 0.566 3.332 dincemp 9.008 1.919 42.276 <some output omitted>
Page 292 bottom of the page
NOTE: The likelihood ratio chi-square values needed are given in the output for the two models shown above: 16.83-8.6 = 8.23.
Page 298 middle of the page
data depress; set depress; if age < 28 then age0 = 1; else age0 = 0; if age >=28 & age <= 42 then age1 = 1; else age1 = 0; if age >=43 & age <= 58 then age2 = 1; else age2 = 0; if age >=59 & age <= 89 then age3 = 1; else age3 = 0; run;
proc logistic data = depress desc; model cases = age1 age2 age3 income sex; run; quit;
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -2.1595 0.7830 7.6056 0.0058 age1 1 0.0747 0.4318 0.0299 0.8626 age2 1 -0.5706 0.4744 1.4468 0.2290 age3 1 -0.8853 0.4563 3.7643 0.0524 income 1 -0.0380 0.0149 6.5298 0.0106 sex 1 0.9238 0.3864 5.7147 0.0168
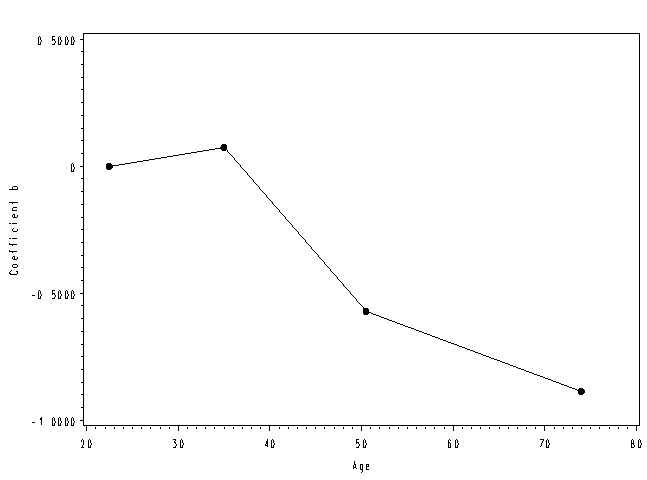
Page 299 Figure 12.2 Estimated coefficients for age quartiles by midpoint of the quartile
NOTE: We need to use ODS to capture the coefficients in a data set. We use the ods trace on and ods trace off statements so that SAS prints the names of the various tables in the log. Then we can look there to get the name of the table that we need to include on the ods output statement. The print procedures are not necessary; they just help see what the data sets look like before the next addition or modification.
ods trace on; proc logistic data = depress desc; model cases = age1 age2 age3 income sex; ods output ParameterEstimates = parms1; run; quit; ods trace off;
proc print data = parms1; run;
data parms1; if _n_ = 1 then do; variable = "age0"; estimate = 0; end; output; set parms1; run;
data parms;
set parms1;
if variable = "age0" then newage = 22.5;
if variable = "age1" then newage = 35;
if variable = "age2" then newage = 50.5;
if variable = "age3" then newage = 74;
if variable in("age0" "age1" "age2" "age3");
run;
proc print data = parms; run;
axis1 label=(a=90 'Coefficient b') order = (-1 to .5 by .5);
axis2 label=("Age") order = (20 to 80 by 10);
symbol1 i=join v=dot;
proc gplot data = parms;
plot estimate*newage / vaxis=axis1 haxis = axis2;
run;
quit;
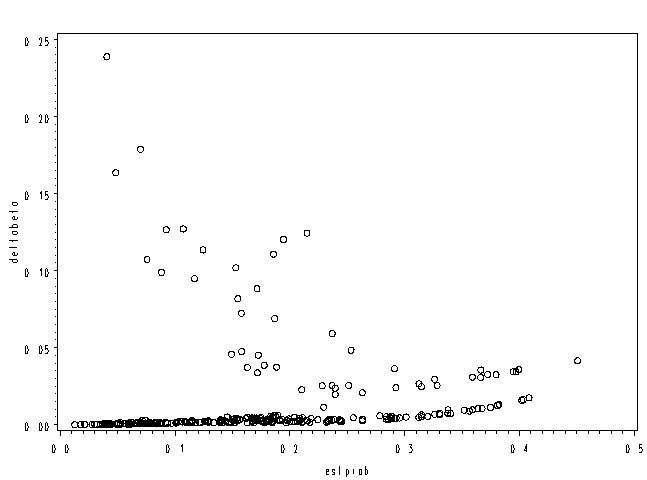
Page 302 Figure 12.3 Delta beta measures to assess the influence of individual patterns on estimated coefficients
NOTE: We are including the difchisq (delta chi-square) statistic here for use on page 305.
proc logistic data = depress desc; model cases = sex income age; output out=pred p=estprob c=deltabeta DIFCHISQ=deltachi; run; quit;
symbol1 i=none v=circle ; axis1 order=(0 to .5 by .1) ; axis2 label=(angle=90) order=(0 to .25 by .05); proc gplot data=pred; plot deltabeta*estprob / haxis=axis1 vaxis=axis2; run; quit;
Page 303 Table 12.2 Percent change in estimated parameters when including and excluding influential patterns
*line 1 of table; proc logistic data = depress desc; model cases = age income sex; run; quit;
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.6059 0.8465 3.5987 0.0578 age 1 -0.0210 0.00904 5.3744 0.0204 income 1 -0.0366 0.0141 6.7343 0.0095 sex 1 0.9294 0.3858 5.8032 0.0160
proc sort data = pred1; by deltabeta; run; proc print data = pred1(firstobs=292); var id deltabeta; run;
Obs id deltabeta
292 288 0.16373 293 99 0.17896 294 68 0.23899
data pred1; set pred; x = 0; if deltabeta > .1637310 then x = 3; if deltabeta > .1789604 then x = 2; if deltabeta > .2084397 then x = 1; run; proc print data = pred1; var x deltabeta; where x ne 0; run;
Obs x deltabeta
292 3 0.16373 293 2 0.17896 294 1 0.23899
* line 2 of table; proc logistic data = pred1 desc; model cases = age income sex; where x ne 1; run; quit;
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.6991 0.8737 3.7818 0.0518 age 1 -0.0215 0.00912 5.5826 0.0181 income 1 -0.0421 0.0150 7.8971 0.0050 sex 1 1.0301 0.4008 6.6050 0.0102
* line 3 of table; proc logistic data = pred1 desc; model cases = age income sex; where x ne 2; run; quit;
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.7570 0.8712 4.0674 0.0437 age 1 -0.0234 0.00925 6.4023 0.0114 income 1 -0.0358 0.0142 6.3918 0.0115 sex 1 1.0505 0.4008 6.8707 0.0088
* line 4 of table; proc logistic data = pred1 desc; model cases = age income sex; where x ne 3; run; quit;
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.7138 0.8721 3.8619 0.0494 age 1 -0.0229 0.00920 6.1894 0.0129 income 1 -0.0389 0.0145 7.1596 0.0075 sex 1 1.0419 0.4009 6.7562 0.0093
* line 5 of table; proc logistic data = pred1 desc; model cases = age income sex; where x = 0; run; quit;
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard Wald Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -2.0252 0.9419 4.6233 0.0315 age 1 -0.0263 0.00953 7.6125 0.0058 income 1 -0.0443 0.0156 8.0351 0.0046 sex 1 1.3094 0.4407 8.8267 0.0030
Page 304 Table 12.3 Estimated probability of being a case (p-hat) for five influential observations
proc print data = pred1 noobs round; var id age income sex cases estprob; where id = 288 or id = 99 or id = 143 or id = 232 or id = 68; run;
143 40 45 1 0 0.04 232 40 45 1 0 0.04 288 61 28 1 1 0.05 99 72 11 1 1 0.07 68 40 45 1 1 0.04
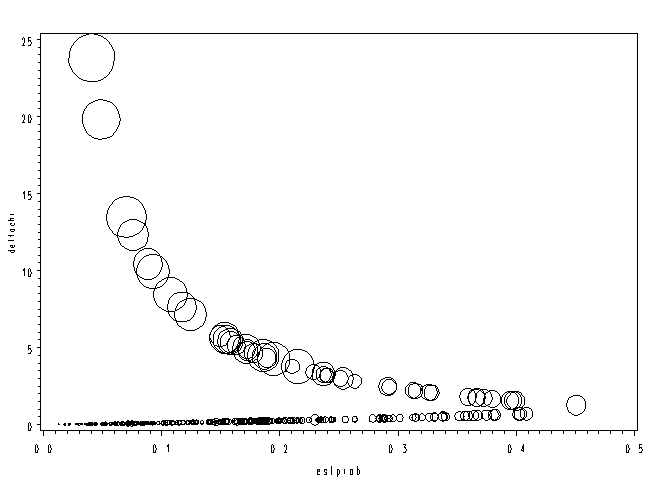
Page 305 Figure 12.4 Delta chi-square measure to assess influence of pattern on overall fit with symbol size proportional to delta beta
NOTE: This graph looks slightly different from the graph in the text. This is probably because SAS and Stata calculate the covariate patterns in different ways.
symbol1 color=black interpol=r value=circle height=1; axis1 order=(0 to 25 by 5) label=(angle=90 color=black height=0.75); axis2 order=(0 to .5 by .1); proc gplot data=pred; bubble deltachi*estprob=deltabeta / bsize=20 haxis=axis2 vaxis=axis1; run; quit;
Page 307 Figure 12.5 Percentage of individuals correctly classified by logistic regression.
NOTE: We were unable to reproduce this graph.
Page 307 Figure 12.6 ROC curve from logistic regression for the depression data set.
NOTE: We were unable to reproduce this graph.