Page 341 Table 13.2 Kaplan-Meier estimates for data from Figure 13.2
data temp; input id years dead; cards; 1 2 1 2 6 1 3 2 0 4 3 0 5 1 1 ; run;
ods select ProductLimitEstimates; proc lifetest data = temp; time years*dead(0); run; quit;
The LIFETEST Procedure
Product-Limit Survival Estimates
Survival
Standard Number Number
years Survival Failure Error Failed Left
0.00000 1.0000 0 0 0 5 1.00000 0.8000 0.2000 0.1789 1 4 2.00000 0.6000 0.4000 0.2191 2 3 2.00000* . . . 2 2 3.00000* . . . 2 1 6.00000 0 1.0000 0 3 0
NOTE: The marked survival times are censored observations.
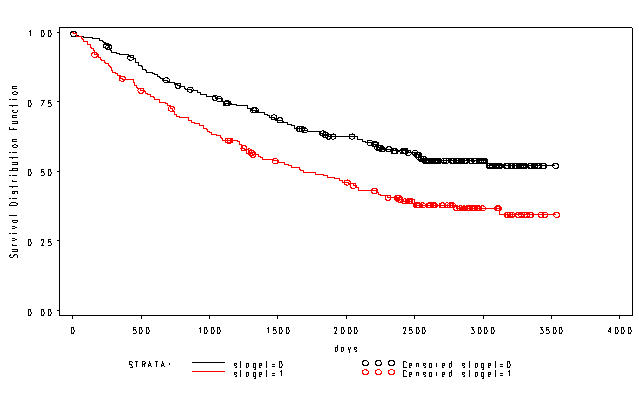
Page 342 Figure 13.6 Kaplan-Meier estimates of the survival functions for lung cancer data
NOTE: You cannot specify a path name on the proc lifetest statement; hence, we have created a temporary data set that is identical to the permanent one and used that.
data surv; set 'd:surv'; run; proc lifetest data = surv plots=(s) method=km; time days*death(0); strata staget; run;
Page 347 Table 13.3 Percentage of deaths versus explanatory variables
data surv; set "c:cama4surv"; run; proc freq data = surv; tables death*(staget perfbl treat poinf) / nopercent nofreq norow; run;
The FREQ Procedure
Table of DEATH by POINF
DEATH POINF
Col Pct | 0| 1| Total
--------+--------+--------+
0 | 50.26 | 25.00 |
--------+--------+--------+
1 | 49.74 | 75.00 |
--------+--------+--------+
Total 380 20 400
Frequency Missing = 1
Page 348 Table 13.4 Log-linear model for lung cancer data: results
NOTE: The intercept given in the output is slightly different from that shown in the text. We suspect that the difference is caused by a change in the algorithms used in the different versions of SAS (an earlier version of SAS was used to generate the output shown in the text).
proc lifereg data = surv; model days*death(0) = staget perfbl treat poinf /d=weibull; run;
The LIFEREG Procedure
Model Information
Data Set WORK.SURV
Dependent Variable Log(DAYS)
Censoring Variable DEATH
Censoring Value(s) 0
Number of Observations 398
Noncensored Values 203
Right Censored Values 195
Left Censored Values 0
Interval Censored Values 0
Missing Values 3
Name of Distribution Weibull
Log Likelihood -512.7478113
Algorithm converged.
Type III Analysis of Effects
Wald
Effect DF Chi-Square Pr > ChiSq
STAGET 1 13.9320 0.0002
PERFBL 1 8.7069 0.0032
TREAT 1 0.2891 0.5908
POINF 1 5.3193 0.0211
Analysis of Parameter Estimates
Standard 95% Confidence Chi-
Parameter DF Estimate Error Limits Square Pr > ChiSq
Intercept 1 8.6423 0.1584 8.3319 8.9527 2977.08 <.0001
STAGET 1 -0.5874 0.1574 -0.8959 -0.2790 13.93 0.0002
PERFBL 1 -0.5986 0.2029 -0.9963 -0.2010 8.71 0.0032
TREAT 1 -0.0831 0.1546 -0.3860 0.2198 0.29 0.5908
POINF 1 -0.7124 0.3089 -1.3178 -0.1070 5.32 0.0211
Scale 1 1.0894 0.0679 0.9641 1.2309
Weibull Shape 1 0.9180 0.0572 0.8124 1.0373
Page 349 Table 13.5 Cox’s model for lung cancer data: results
proc phreg data = surv; model days*death(0) = staget perfbl treat poinf; run;
The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
STAGET 1 0.53654 0.14211 14.2542 0.0002 1.710
PERFBL 1 0.53080 0.18524 8.2110 0.0042 1.700
TREAT 1 0.07036 0.14182 0.2461 0.6198 1.073
POINF 1 0.66690 0.28040 5.6566 0.0174 1.948
We have skipped the examples on pages 350-354 because they use a simulated data set.
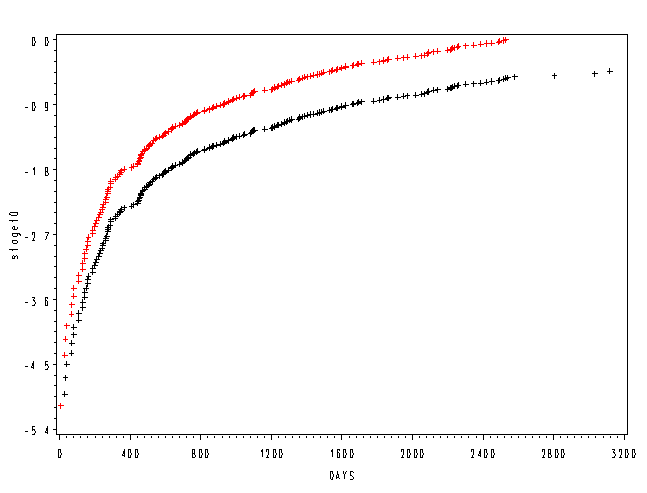
Page 357 Figure 13.9 Computer-generated graph of log(-logS(t)) versus t for lung cancer data (A = large tumor, B = small tumor)
data cov; staget = 0; perfbl = .1553885; treat = .5137157; poinf = .050; run; proc phreg data = surv; model days*death(0) = staget perfbl treat poinf; baseline covariates=cov loglogs=staget0 out=out0 / nomean; run; data cov1; staget = 1; perfbl = .1553885; treat = .5137157; poinf = .050; run; proc phreg data = surv; model days*death(0) = staget perfbl treat poinf; baseline covariates=cov1 loglogs=staget1 out=out1 / nomean; run; data fig138; merge out0 out1; by days; run; axis1 order=(0 to 3200 by 400); axis2 order=(-5.4 to 0 by .9) label=(a=90); proc gplot data = fig138; plot (staget0 staget1)*days / overlay haxis=axis1 vaxis=axis2; run; quit;