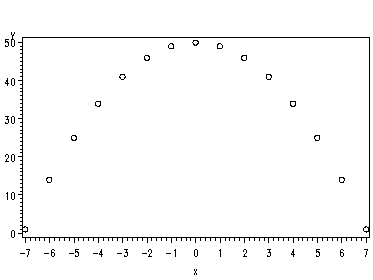This page shows how to obtain the results from Chatterjee, Hadi and Price’s Chapter 2 using SAS.
Use data in file p025a. Note the semicolon on the line following after the data indicates the end of the data.
options nocenter; data p025a; input y x; datalines; 1 -7 14 -6 25 -5 34 -4 41 -3 46 -2 49 -1 50 0 49 1 46 2 41 3 34 4 25 5 14 6 1 7 ; run;
Table 2.3, page 25.
proc print data=p025a; run; Obs y x 1 1 -7 2 14 -6 3 25 -5 4 34 -4 5 41 -3 6 46 -2 7 49 -1 8 50 0 9 49 1 10 46 2 11 41 3 12 34 4 13 25 5 14 14 6 15 1 7
Figure 2.2, page 25.
Note: The symbol statement before proc gplot sets the plotting symbol for the scatter plot to a circle.
symbol1 v=circle; proc gplot data=p025a; plot y*x; run;
Use data in file p025b.
data p025b; input y1 x1 y2 x2 y3 x3 y4 x4; datalines; 8.04 10 9.14 10 7.46 10 6.58 8 6.95 8 8.14 8 6.77 8 5.76 8 7.58 13 8.74 13 12.74 13 7.71 8 8.81 9 8.77 9 7.11 9 8.84 8 8.33 11 9.26 11 7.81 11 8.47 8 9.96 14 8.1 14 8.84 14 7.04 8 7.24 6 6.13 6 6.08 6 5.25 8 4.26 4 3.1 4 5.39 4 12.5 19 10.84 12 9.13 12 8.15 12 5.56 8 4.82 7 7.26 7 6.42 7 7.91 8 5.68 5 4.74 5 5.73 5 6.89 8 ; run;
Part of Table 2.4, page 25.
proc print data=p025b; run; Obs y1 x1 y2 x2 y3 x3 y4 x4 1 8.04 10 9.14 10 7.46 10 6.58 8 2 6.95 8 8.14 8 6.77 8 5.76 8 3 7.58 13 8.74 13 12.74 13 7.71 8 4 8.81 9 8.77 9 7.11 9 8.84 8 5 8.33 11 9.26 11 7.81 11 8.47 8 6 9.96 14 8.10 14 8.84 14 7.04 8 7 7.24 6 6.13 6 6.08 6 5.25 8 8 4.26 4 3.10 4 5.39 4 12.50 19 9 10.84 12 9.13 12 8.15 12 5.56 8 10 4.82 7 7.26 7 6.42 7 7.91 8 11 5.68 5 4.74 5 5.73 5 6.89 8
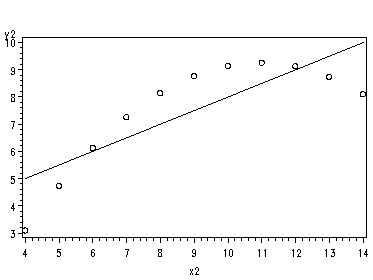
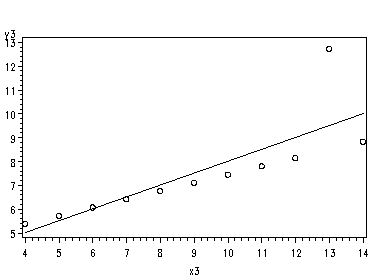
Fig. 2.3(a), page 26.
Note: The i=r in the symbol statement includes the regression line in the scatter plot.
symbol1 v=circle i=r; proc gplot data=p025b; plot y1*x1; plot y2*x2; plot y3*x3 plot y4*x4; run;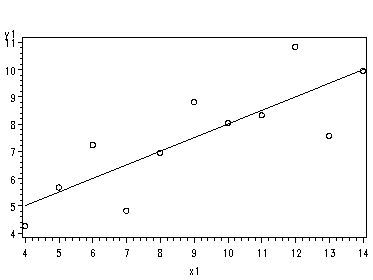
Use data in file p027.
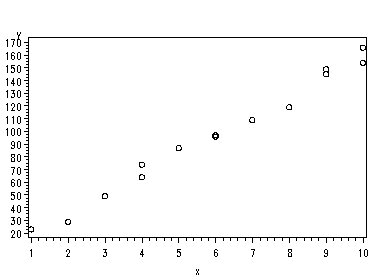
data p027; input y x; datalines; 23 1 29 2 49 3 64 4 74 4 87 5 96 6 97 6 109 7 119 8 149 9 145 9 154 10 166 10 ; run;
Commands to create Table 2.6,page 28.
Note: New variables are created in the datastep. The set statement starts the data step with the observations in the SAS dataset p027.
proc means data=p027; run; The MEANS Procedure Variable N Mean Std Dev Minimum Maximum ------------------------------------------------------------------------------ y 14 97.2142857 46.2171772 23.0000000 166.0000000 x 14 6.0000000 2.9612887 1.0000000 10.0000000 ------------------------------------------------------------------------------ data p027a; set p027; dy = y - 97.21; dx = x - 6; dy2 = dy**2; dx2 = dx**2; dxy = dx*dy; run;
Table 2.6, page 28.
proc print data=p027a; run; Obs y x dy dx dy2 dx2 dxy 1 23 1 -74.21 -5 5507.12 25 371.05 2 29 2 -68.21 -4 4652.60 16 272.84 3 49 3 -48.21 -3 2324.20 9 144.63 4 64 4 -33.21 -2 1102.90 4 66.42 5 74 4 -23.21 -2 538.70 4 46.42 6 87 5 -10.21 -1 104.24 1 10.21 7 96 6 -1.21 0 1.46 0 0.00 8 97 6 -0.21 0 0.04 0 0.00 9 109 7 11.79 1 139.00 1 11.79 10 119 8 21.79 2 474.80 4 43.58 11 149 9 51.79 3 2682.20 9 155.37 12 145 9 47.79 3 2283.88 9 143.37 13 154 10 56.79 4 3225.10 16 227.16 14 166 10 68.79 4 4732.06 16 275.16
Fig 2.4, page 28.
Note: The i=none turns off the regression line option.
symbol1 v=circle i=none; proc gplot data=p027; plot y*x; run;
Table 2.9, page 36.
Note: In this example, the output option adds the predicted values, residuals and two standard errors to the original observations in a new SAS dataset named p027b.
proc reg data=p027;
model y = x;
output out=p027b predicted=yhat residual=e stdi=seyhat stdp=semu;
run;
The REG Procedure
Model: MODEL1
Dependent Variable: y
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 27420 27420 943.20 <.0001
Error 12 348.84837 29.07070
Corrected Total 13 27768
Root MSE 5.39172 R-Square 0.9874
Dependent Mean 97.21429 Adj R-Sq 0.9864
Coeff Var 5.54623
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 4.16165 3.35510 1.24 0.2385
x 1 15.50877 0.50498 30.71 <.0001
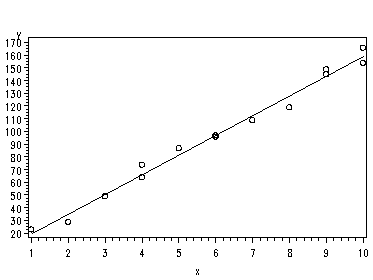
Table 2.7, page 32.
proc print data=p027b; var yhat e; run; Obs yhat e 1 19.670 3.32957 2 35.179 -6.17920 3 50.688 -1.68797 4 66.197 -2.19674 5 66.197 7.80326 6 81.706 5.29449 7 97.214 -1.21429 8 97.214 -0.21429 9 112.723 -3.72306 10 128.232 -9.23183 11 143.741 5.25940 12 143.741 1.25940 13 159.249 -5.24937 14 159.249 6.75063
Fig. 2.5, page 32.
symbol1 v=circle i=r; proc gplot data=p027; plot y*x; run;
Standard error for a predicted score, page 39.
proc print data=p027b; var seyhat; run; Obs seyhat 1 6.12555 2 5.93526 3 5.78293 4 5.67161 5 5.67161 6 5.60376 7 5.58097 8 5.58097 9 5.60376 10 5.67161 11 5.78293 12 5.78293 13 5.93526 14 5.93526
Standard error for mean prediction, page 39.
proc print data=p027b; var y x semu; run; Obs y x semu 1 23 1 2.90717 2 29 2 2.48124 3 49 3 2.09082 4 64 4 1.75969 5 74 4 1.75969 6 87 5 1.52692 7 96 6 1.44100 8 97 6 1.44100 9 109 7 1.52692 10 119 8 1.75969 11 149 9 2.09082 12 145 9 2.09082 13 154 10 2.48124 14 166 10 2.48124
Correlations, page 43.
proc corr data=p027b;
var y x yhat;
run;
The CORR Procedure
Pearson Correlation Coefficients, N = 14
Prob > |r| under H0: Rho=0
y x yhat
y 1.00000 0.99370 0.99370
<.0001 <.0001
x 0.99370 1.00000 1.00000
<.0001 <.0001
yhat 0.99370 1.00000 1.00000
Predicted Value of y <.0001 <.0001