This page shows how to obtain the results from Chatterjee, Hadi and Price’s Chapter 12 using SAS. The first example uses the p323 data file. You can copy and paste this data step into the program editor to run the examples below.
Note: The variable index corresponds to the row value in Table 12.1. The statement, index+1;, is one way to create a case ID in SAS. The +1 indicates that SAS is to add one to each successive case.
data p323; set p323; index = +1; run;
Table 12.1, page 323.
proc print data=p323; run; Obs Y X1 X2 X3 index 1 0 -62.8 -89.5 1.7 1 2 0 3.3 -3.5 1.1 1 3 0 -120.8 -103.2 2.5 1 4 0 -18.1 -28.8 1.1 1 5 0 -3.8 -50.6 0.9 1 6 0 -61.2 -56.2 1.7 1 7 0 -20.3 -17.4 1.0 1 8 0 -194.5 -25.8 0.5 1 9 0 20.8 -4.3 1.0 1 10 0 -106.1 -22.9 1.5 1 11 0 -39.4 -35.7 1.2 1 12 0 -164.1 -17.7 1.3 1 13 0 -308.9 -65.8 0.8 1 14 0 7.2 -22.6 2.0 1 15 0 -118.3 -34.2 1.5 1 16 0 -185.9 -280.0 6.7 1 17 0 -34.6 -19.4 3.4 1 18 0 -27.9 6.3 1.3 1 19 0 -48.2 6.8 1.6 1 20 0 -49.2 -17.2 0.3 1 21 0 -19.2 -36.7 0.8 1 22 0 -18.1 -6.5 0.9 1 23 0 -98.0 -20.8 1.7 1 24 0 -129.0 -14.2 1.3 1 25 0 -4.0 -15.8 2.1 1 26 0 -8.7 -36.3 2.8 1 27 0 -59.2 -12.8 2.1 1 28 0 -13.1 -17.6 0.9 1 29 0 -38.0 1.6 1.2 1 30 0 -57.9 0.7 0.8 1 31 0 -8.8 -9.1 0.9 1 32 0 -64.7 -4.0 0.1 1 33 0 -11.4 4.8 0.9 1 34 1 43.0 16.4 1.3 1 35 1 47.0 16.0 1.9 1 36 1 -3.3 4.0 2.7 1 37 1 35.0 20.8 1.9 1 38 1 46.7 12.6 0.9 1 39 1 20.8 12.5 2.4 1 40 1 33.0 23.6 1.5 1 41 1 26.1 10.4 2.1 1 42 1 68.6 13.8 1.6 1 43 1 37.3 33.4 3.5 1 44 1 59.0 23.1 5.5 1 45 1 49.6 23.8 1.9 1 46 1 12.5 7.0 1.8 1 47 1 37.3 34.1 1.5 1 48 1 35.3 4.2 0.9 1 49 1 49.5 25.1 2.6 1 50 1 18.1 13.5 4.0 1 51 1 31.4 15.7 1.9 1 52 1 21.5 -14.4 1.0 1 53 1 8.5 5.8 1.5 1 54 1 40.6 5.8 1.8 1 55 1 34.6 26.4 1.8 1 56 1 19.9 26.7 2.3 1 57 1 17.4 12.6 1.3 1 58 1 54.7 14.6 1.7 1 59 1 53.5 20.6 1.1 1 60 1 35.9 26.4 2.0 1 61 1 39.4 30.5 1.9 1 62 1 53.1 7.1 1.9 1 63 1 39.8 13.8 1.2 1 64 1 59.5 7.0 2.0 1 65 1 16.3 20.4 1.0 1 66 1 21.7 -7.8 1.6 1
Table 12.2, page 324.
Note 1: The descending option is needed so that SAS will model the probability of a response value of 1. By default, SAS models the probability of the response corresponding to the lower ordered value.
Note 2: The output statement creates an output dataset containing predicted probabilities, deviance residuals, Pearson residual, leverage, and change in chi-squared statistics.
proc logistic data=p323 descending;
model y = x1 x2 x3 / iplots;
output out=p323o prob=p resdev=dr h=pii
reschi=pr cbar=dbeta difchisq=dfg;
run;
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -10.1527 10.8389 0.8774 0.3489
X1 1 0.3312 0.3007 1.2133 0.2707
X2 1 0.1809 0.1069 2.8617 0.0907
X3 1 5.0871 5.0816 1.0022 0.3168
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
X1 1.393 0.772 2.511
X2 1.198 0.972 1.478
X3 161.922 0.008 >999.999
Association of Predicted Probabilities and Observed Responses
Percent Concordant 99.9 Somers' D 0.998
Percent Discordant 0.1 Gamma 0.998
Percent Tied 0.0 Tau-a 0.507
Pairs 1089 c 0.999
-------+---+---+---+---+---+---+---+---+---+---+---+---+---+---+-------
2 + +
| |
P | |
e | * |
a | |
r 1 + +
s | |
o RESCHI | * |
n | |
| * * * ** |
R 0 + ****** *** ******** ******** ******* **** ********* +
e | * * |
s | * |
i | |
d | |
u -1 + +
a | |
l | |
| * |
| |
-2 + +
-------+---+---+---+---+---+---+---+---+---+---+---+---+---+---+-------
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70
Case Number INDEX
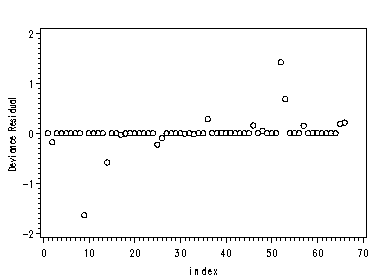
Fig 12.2 page 326.
-------+---+---+---+---+---+---+---+---+---+---+---+---+---+---+-------
2 + +
| |
D | |
e | * |
v | |
i 1 + +
a |
n RESDEV | * |
c | |
e | * * * ** |
0 + ****** *** ******** ******** ******* **** ********* +
R | * * |
e | |
s | * |
i | |
d -1 + +
u | |
a | |
l | * |
| |
-2 + +
-------+---+---+---+---+---+---+---+---+---+---+---+---+---+---+-------
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70
Case Number INDEX
-+----+----+----+----+----+----+----+----+----+----+----+----+----+----+--
0.8 + +
| |
| |
| |
H | * |
a 0.6 + * +
t | * |
H | |
D | * |
i | |
a 0.4 + * +
g | * |
o | |
n | |
a | * * |
l 0.2 + +
| * |
| |
| * * * |
| * * |
0.0 + * ****** **** ** ******* ********* ********* * *** *** ******* +
-+----+----+----+----+----+----+----+----+----+----+----+----+----+----+--
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70
Case Number INDEX
------+---+---+---+---+---+---+---+---+---+---+---+---+---+---+-------
DFBETA0 | |
0.4 + +
I | |
n | * |
t | |
e | |
r | |
c 0.2 + +
e | * |
p | |
t | |
| |
D | |
f 0.0 + ****** *** ******** ******** ******* **** ********** +
B | * |
e | * * |
t | * * |
a | * |
| |
-0.2 + +
| |
------+---+---+---+---+---+---+---+---+---+---+---+---+---+---+-------
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70
Case Number INDEX
------+---+---+---+---+---+---+---+---+---+---+---+---+---+---+-------
DFBETA1 | |
0.2 + * +
| |
| |
| * * * * |
| |
X | * |
1 0.0 + ****** *** ******** ******** ******* **** ********** +
| * |
D | |
f | |
B | |
e | |
t -0.2 + +
a | |
| |
| |
| * |
| |
-0.4 + * +
| |
------+---+---+---+---+---+---+---+---+---+---+---+---+---+---+-------
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70
Case Number INDEX
------+---+---+---+---+---+---+---+---+---+---+---+---+---+---+-------
0.5 + * * +
| |
| |
| |
| * * * |
0.0 + ****** *** ******** ******** ************ ********* * +
X | |
2 DFBETA2 | |
| |
D | * |
f -0.5 + +
B | |
e | |
t | |
a | |
-1.0 + +
| * |
| |
| |
| |
-1.5 + +
------+---+---+---+---+---+---+---+---+---+---+---+---+---+---+-------
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70
Case Number INDEX
------+---+---+---+---+---+---+---+---+---+---+---+---+---+---+-------
0.2 + +
| * |
| * |
| * * |
| * * |
0.0 + ****** *** ******** ******** ******* **** ********** +
X | |
3 DFBETA3 | |
| |
D | |
f -0.2 + * +
B | * |
e | |
t | |
a | |
-0.4 + +
| |
| * |
| |
| |
-0.6 + +
------+---+---+---+---+---+---+---+---+---+---+---+---+---+---+-------
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70
Case Number INDEX
--+----+----+----+----+----+----+----+----+----+----+----+----+----+----+---
C 8 + +
o | |
n | |
f | |
i | * |
d 6 + +
e | |
n C | |
c | |
e | |
4 + +
I | |
n | |
t | * |
e | |
r 2 + +
v | |
a | |
l | * * |
| |
D 0 + ******** **** ************************************* ************* +
i --+----+----+----+----+----+----+----+----+----+----+----+----+----+----+---
s 0 5 10 15 20 25 30 35 40 45 50 55 60 65 70
p
Case Number INDEX
Fig 12.3, page 326.
-+----+----+----+----+----+----+----+----+----+----+----+----+----+----+-
C CBAR | |
o 3 + +
n | |
f | |
i | * |
d | |
e | |
n 2 + +
c | * |
e | |
| |
I | |
n | |
t 1 + +
e | |
r | |
v | |
a | * * |
l | |
0 + ******** **** ************************************* ************* +
D | |
i -+----+----+----+----+----+----+----+----+----+----+----+----+----+----+-
s 0 5 10 15 20 25 30 35 40 45 50 55 60 65 70
p
Case Number INDEX
-------+---+---+---+---+---+---+---+---+---+---+---+---+---+---+-------
DIFDEV | |
6 + +
| |
D | |
e | |
l | * * |
t | |
a 4 + +
| |
D | |
e | |
v | |
i | |
a 2 + +
n | |
c | |
e | |
| * * |
| |
0 + ****** *** ****************************** *********** +
| |
-------+---+---+---+---+---+---+---+---+---+---+---+---+---+---+-------
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70
Case Number INDEX
Fig 12.4, page 327.
------+---+---+---+---+---+---+---+---+---+---+---+---+---+---+------
DIFCHISQ | |
6 + +
| |
D | |
e | |
l | * |
t | * |
a 4 + +
| |
C | |
h | |
i | |
S | |
q 2 + +
u | |
a | |
r | |
e | * * |
| |
0 + ****** *** ****************************** *********** +
| |
------+---+---+---+---+---+---+---+---+---+---+---+---+---+---+------
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70
Case Number INDEX
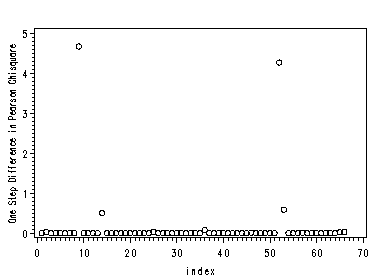
Figures 12.2 and 12.4, pages 326 and 327.
Note 1: Observations 9 and 52 appear are clearly problematic, however observation 36 does not appear problematic differing from the figures in the book.
Note 2: The symbol and axis statements are used to define the plotting symbol (circle) and to display the Y-axis label vertically.
symbol1 v=circle; axis1 label=(r=1 a=90); proc gplot data=p323o; plot dr*index; plot dfg*index; run;
Table 12.3, page 328.
proc logistic data=p323 descending;
model y = x1 x2;
run;
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -0.5503 0.9510 0.3349 0.5628
X1 1 0.1574 0.0749 4.4114 0.0357
X2 1 0.1947 0.1224 2.5297 0.1117
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
X1 1.170 1.011 1.356
X2 1.215 0.956 1.544
Association of Predicted Probabilities and Observed Responses
Percent Concordant 99.7 Somers' D 0.994
Percent Discordant 0.3 Gamma 0.994
Percent Tied 0.0 Tau-a 0.505
Pairs 1089 c 0.997
Table 12.4, page 328.
proc logistic data=p323 descending;
model y = x1;
run;
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -1.1666 0.8164 2.0418 0.1530
X1 1 0.1767 0.0571 9.5775 0.0020
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
X1 1.193 1.067 1.335
Association of Predicted Probabilities and Observed Responses
Percent Concordant 99.1 Somers' D 0.983
Percent Discordant 0.8 Gamma 0.983
Percent Tied 0.1 Tau-a 0.499
Pairs 1089 c 0.991
Table 12.5, page 331.
proc reg data=p323;
model y = x1 x2 x3;
output out=p323o2 predicted=p;
run;
end;
The REG Procedure
Model: MODEL1
Dependent Variable: Y
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 9.40334 3.13445 27.38 <.0001
Error 62 7.09666 0.11446
Corrected Total 65 16.50000
Root MSE 0.33832 R-Square 0.5699
Dependent Mean 0.50000 Adj R-Sq 0.5491
Coeff Var 67.66456
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 0.32187 0.08746 3.68 0.0005
X1 1 0.00312 0.00082939 3.76 0.0004
X2 1 0.00425 0.00144 2.96 0.0044
X3 1 0.14850 0.04532 3.28 0.0017
Table 12.6, page 332.
Note: the command assign = (p >= .5) creates a new variable assign which has the value 1 if p is greater or equal to .5 and 0 otherwise.
data p323r; set p323o2; assign = (p >= .5); run; proc print data=p323r; var y p assign; run; Obs Y p assign 1 0 -0.00170 0 2 0 0.48066 0 3 0 -0.12212 0 4 0 0.30644 0 5 0 0.22883 0 6 0 0.14467 0 7 0 0.33313 0 8 0 -0.32057 0 9 0 0.51704 1 10 0 0.11620 0 11 0 0.22551 0 12 0 -0.07248 0 13 0 -0.80295 0 14 0 0.54540 1 15 0 0.03014 0 16 0 -0.45225 0 17 0 0.63641 1 18 0 0.45458 0 19 0 0.43788 0 20 0 0.13981 0 21 0 0.22492 0 22 0 0.37142 0 23 0 0.18010 0 24 0 0.05195 0 25 0 0.55416 1 26 0 0.55640 1 27 0 0.39458 0 28 0 0.33990 0 29 0 0.38824 0 30 0 0.26290 0 31 0 0.38941 0 32 0 0.11777 0 33 0 0.44031 0 34 1 0.71878 1 35 1 0.81867 1 36 1 0.72951 1 37 1 0.80159 1 38 1 0.65479 1 39 1 0.79627 1 40 1 0.74783 1 41 1 0.75935 1 42 1 0.83220 1 43 1 1.09987 1 44 1 1.42088 1 45 1 0.85990 1 46 1 0.65791 1 47 1 0.80583 1 48 1 0.58354 1 49 1 0.96906 1 50 1 1.02970 1 51 1 0.76870 1 52 1 0.47635 0 53 1 0.59578 1 54 1 0.74053 1 55 1 0.80927 1 56 1 0.83890 1 57 1 0.62273 1 58 1 0.80706 1 59 1 0.73969 1 60 1 0.84302 1 61 1 0.85651 1 62 1 0.79992 1 63 1 0.68290 1 64 1 0.83433 1 65 1 0.60786 1 66 1 0.59409 1